静基座下惯性平台初始自对准技术
2017-07-07丁智坚张士峰杨华波
丁智坚,周 欢,张士峰,杨华波,蔡 洪
(1. 中国空气动力研究与发展中心吸气式高超声速技术研究中心,绵阳621000;2. 中国工程物理研究院总体工程研究所,绵阳621900;3. 国防科学技术大学航天科学与工程学院,长沙410073)
静基座下惯性平台初始自对准技术
丁智坚1,周 欢2,张士峰3,杨华波3,蔡 洪3
(1. 中国空气动力研究与发展中心吸气式高超声速技术研究中心,绵阳621000;2. 中国工程物理研究院总体工程研究所,绵阳621900;3. 国防科学技术大学航天科学与工程学院,长沙410073)
针对框架式惯性平台系统能够绕框架轴自主转动的特点,提出一种基于粗对准+精对准的静基座下惯性平台快速初始自对准方法。该方法首先利用重力矢量随地球自转的特点,快速实现惯性平台的粗对准。在此基础上,通过设计加矩方案令平台绕天向轴旋转并采用Kalman滤波技术,完成惯性平台的精对准。仿真算例表明,该方法能够在720s内实现惯性平台水平姿态角小于5"(1σ),方位姿态角小于12"(1σ)的自对准精度,有效地提高了系统的响应速度和导航精度。
惯性平台;初始自对准;Kalman滤波;静基座
0 引 言
惯性平台导航系统凭借其高精度的优势一直作为战略导弹等武器系统导航制导与控制系统的核心设备[1-2]。同所有惯性导航系统一样,惯性平台在使用前需进行初始对准[3-5],其结果将直接影响武器系统的响应速度和打击精度[6]。因此,一种快而准的惯性平台初始对准技术一直是研究人员所追寻的目标[7-15]。
“调平”+“瞄准”方法是惯性平台初始对准中常见的方法[9]。其中“调平”是指利用平台上两个水平加速度计,通过调平回路将平台台体调整至与水平面平行[9,16];“瞄准”是指在“调平”的基础上,通过瞄准回路和多位置法进行寻北,完成惯性平台的方位对准[16]。这种方法的基本原理浅显易懂,采用的算法简单,故在工程上得到了广泛的应用。
然而,该方案存在以下缺陷[9-16]:
1) 对准与导航中惯性平台工作状态不一致。稳定回路与调平回路和瞄准回路是惯性平台常见的三种工作状态。采用“调平”+“瞄准”的方案时,平台工作于调平回路和瞄准回路,而在实际导航中,平台工作于稳定回路中[17]。由于不同的工作状态导致惯性平台的误差特性及控制回路性能均不一样,导致该方案的对准结果存在一定的偏差。
2) 对准时间较长。三浮陀螺仪在实际使用中,其浮子对外界运动信息较为敏感。特别地,在多位置瞄准过程中,当平台粗加矩和精加矩之间相互切换时,即平台由静止转入角运动状态或由角运动转为静止状态时,受浮子运动影响陀螺仪会存在瞬时较大偏差,进而影响系统输出。故工程上通过延长平台在每个静态位置的时间并选用稳定时间段内的数据以保证初始对准的结果受陀螺仪浮子运动影响较小。然而,该方法增加了对准的时间。
3) 无法中断并快速切入导航工作状态。假设惯性平台正在采用该方法进行初始对准,若突然接到发射命令,惯性平台首先要终止初始对准,并迅速归零并装载前次对准结果,进入导航状态。该过程繁琐复杂并对导弹的响应速度产生严重的影响。
针对上述问题,本文展开了惯性平台静基座下的初始对准技术的研究。借鉴捷联惯导系统中基于惯性系粗对准方法[19]的思路,提出了一种采用粗对准+精对准的惯性平台高精度快速初始对准方案。仿真算例表明,本文所提出的方法能够在720s内实现惯性平台水平姿态角小于5"(1σ),方位姿态角小于12"(1σ)的自对准精度,大幅度地提高了导弹的响应速度和打击精度。
1 静基座下惯性平台粗对准方案
如图1所示,从惯性空间角度看,地球上某处的重力矢量随地球一起绕地球自转轴转动。由于地球自转角速度大小精确已知,故不同时间内同一地点的重力矢量相对惯性空间转动的角度信息中包含了地球北向的信息。因此,基于该特性,利用不同时刻重力矢量在惯性系中的投影等信息即可实现惯性平台的粗对准。
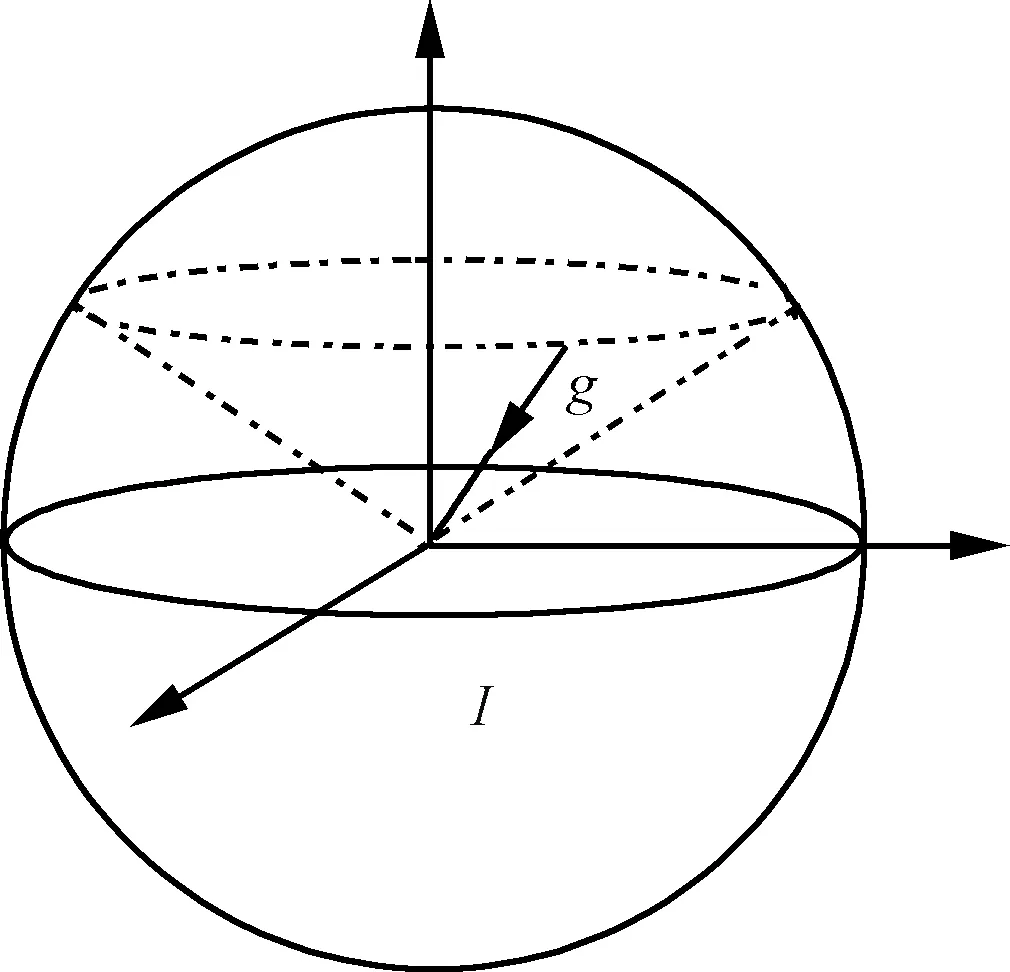
图1 地球上某处重力矢量随地球转动示意图Fig.1 The rotation of the gravity vector along the Earth′s axis
1.1 相应坐标系定义
本文所研究的框架式惯性平台由三个三浮陀螺仪和三个石英加速度计组成,各仪表的安装取向如图2所示[6]。
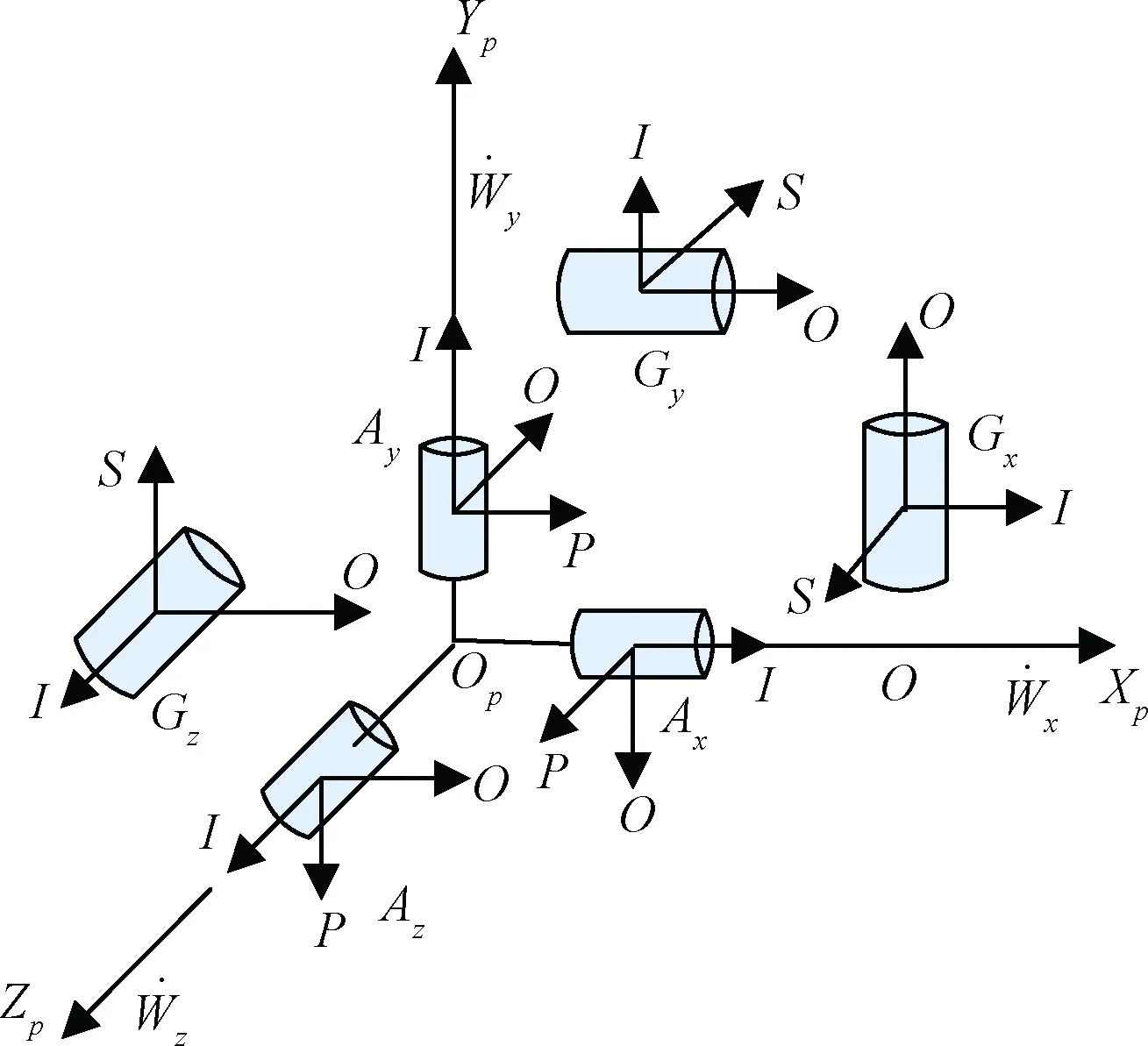
图2 平台几何结构Fig.2 Platform geometry
为了方便后续工作,定义如下坐标系:
1)平台坐标系(p系)
取平台几何中心O为原点,Xp轴与X石英加速度计敏感轴平行,Yp轴平行于X和Y石英加速度计敏感轴所确定的平面,并与Xp轴垂直,Zp轴与Xp轴和Yp轴构成右手坐标系。
2)地心坐标系(e系)
坐标系原点为地心Oe,Xe轴位于赤道平面内,指向地球本初子午线,Ze轴沿地球自转轴指向北极,Ye轴与Xe轴和Ze轴构成右手坐标系。
3)地心惯性坐标系(i系)
坐标系原点为地心Oe,Xi轴指向平台粗对准起始时刻t0所在的子午线,Zi轴沿地球自转轴指向北极,Yi轴与Xi轴和Zi轴构成右手坐标系。
4)平台惯性坐标系(ip0系)
坐标系原点与平台几何中心O重合,选取t0时刻的平台坐标系作为平台惯性坐标系。该坐标系为惯性坐标系,并不随平台转动而转动。
5)计算平台坐标系(c系)
将计算机所建立的数字平台坐标系定义为计算平台坐标系。由于初始对准误差、安装误差以及陀螺仪漂移等误差因素,使得该坐标系与p系并不重合,存在小角度偏差。
6)导航坐标系(n系)
选择当地地理系作为导航坐标系,其Xn轴指向北向,Yn轴指向天向,Zn轴指向东向。
1.2 静基座下惯性平台粗对准方案
设tk时刻,平台所在的地理位置表示为(λk,Lk),其中λk和Lk分别为tk时刻经度与纬度,故此时惯性平台姿态矩阵可写为
(1)

(2)
(3)
式中:θ=ωie(tk-t0),ωie为地球自转角速度大小。
(4)
(5)
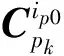
(6)
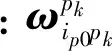
由惯性平台工作原理可知[18-19]
(7)
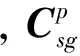
(8)
考虑到式(6)和式(8),短时间段内由平台稳定回路可保证[19]
(9)
此外,对于惯性平台而言,其石英加速度计组的输出可表示为[19-21]
(10)
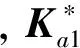
加速度计输入aAI可写为
(11)
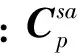
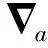
(12)
则式(10)可改写为
(13)
将式(1)代入式(13),有
(14)
将式(1)、(4)、(5)及(9)代入式(14),有
(15)
(16)
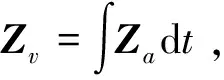
(17)
根据式(17),在t1及t2时刻(t2>t1>t0)有
(18)

(19)
综上所述,静基座下惯性平台粗对准过程如下:
步骤 1. 惯性平台启动、平台框架归零;
步骤2. 惯性平台切换至导航状态,采集加速度计的输出;
2 静基座下惯性平台精对准方案
对比式(18)与(19)可知,粗对准过程中忽略了惯性器件自身误差,故其结果不能满足系统精度要求。通过将平台初始粗对准结果作为滤波器初值,设计加矩方案令平台绕天向旋转,并采用闭环EKF算法,则能够实现静基座下惯性平台精对准。
2.1 系统模型
考虑到初始对准用时较短,可将平台漂移视为小量,故系统模型可用失准角模型描述,即
(20)
式中:φ表示p系与c系之间的误差角矢量,[·×]表示矢量的叉乘矩阵。
考虑到式(7),有
(21)
另一方面,静基座下加速度输出误差可表示为
Z=Za+gc=
(22)
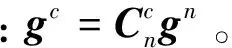
式(21)与式(22)构成了惯性平台静基座下精对准系统模型。
2.2 滤波策略
从式(21)可以看出,随着时间的累积失准角会逐渐变大,不再满足小角度假设条件,进而导致系统模型失效。因此,在使用时,必须采用闭环滤波策略,以此保证失准角始终满足小角度假设,避免因模型失准导致的滤波发散。
对于惯性平台初始对准系统而言,闭环滤波的目的就是通过对系统的调整,使p系与c系重合。传统方法直接利用滤波结果,对平台加矩,调整平台实际的姿态,使p系逐步向c系靠拢。然而该方法需要根据滤波结果对平台进行实时加矩,这对平台控制回路要求较高并存在一定的不可控性,特别地,当滤波结果偏差较大或错误时会将平台姿态调整至错误方向,容易导致平台“飞转”,发生意外。另一方面,传统方法无法进行线下数据处理,所采集的数据对后续试验分析的用处有限。
针对上述问题,本文提出一种基于计算坐标系调整的闭环滤波策略。
这种闭环滤波策略无需对平台姿态进行实时调整,而是利用滤波结果对计算机所建立的计算坐标系进行调整,使c系向p系靠拢,最终实现闭环滤波。同传统方法比,该方案实施较为简单,无需调整平台姿态,保证了平台工作的稳定和安全,同时具有能够实现线下滤波、事后数据处理等优势。
(23)
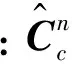
2.3 平台加矩方案设计
由式(21)可知,仅考虑平台失准角与陀螺仪零偏时,系统动力学方程可改写为
(24)
考虑到式(10),忽略高阶小量,式(22)可展开为
(25)
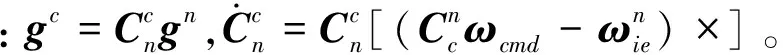
平台加矩方案中所需设计参数主要有加矩大小和加矩方向。本文从状态量可观性角度出发,分析了加矩方案对系统的影响,给出了设计方案。
1)加矩方向设计
(1)ωcmdx=ωcmdy=ωcmdz=0
从式(24)、(25)可以看出,当平台不加矩时,系统模型可表示为
(26)
(27)
(2)ωcmdy≠0,ωcmdx=ωcmdz=0
忽略平台与地理系之间水平方向的小角度,此时加矩方案可近似视为向平台天向加矩。此时有gc≈gn=[0,-1,0]T,系统模型可近似为
(28)
(29)

从理论上看,加速度计输出是系统唯一的观测量,由于重量矢量方向与天向相反,绕天向旋转的加矩方案对系统可观性影响不大,这与捷联系统的结论不一样。
2)加矩大小设计
从式(24)可以看出,当平台转动角速度过大时,由转速引起的失准角增量会远远大于由陀螺零偏作用的效果,进而增加陀螺仪零偏与平台失准角之间的分离难度。而过小的转动角速度,则会增加对准的时间,不满足武器系统快速响应的作战需求。
另一方面,从系统模型可以看出,重力矢量是激励系统的主要因素,而不同的平台位置,则保证了重力矢量在每个轴都有充分的激励。因此,位置可以视为加矩大小的主要设计原则。
3)其他约束条件
由惯性平台工作原理可知,为了避免平台“锁定”,平台中框(Y陀螺)加矩不能超过90°或在90°附近。
此外,为减小平台各轴之间的耦合效应,应避免对平台各轴同时加矩。
综合考虑各方因素,本文设计的加矩方案如下所示:
步骤1. 向平台X方向加矩180s;
步骤2. 向平台Z方向加矩180s;
加矩大小为0.5°/s。
值得注意的是,本文只给出了平台加矩方案的设计准则与约束条件,并在此基础上,设计了一条简单、易实施的非最优的施矩方案。
综上所述,本文所设计的惯性平台初始对准方案共需要780s(包含粗对准60s),13min,且整个对准过程平台工作状态不需切换,加矩方案包含的平台动作较少,实施较为简便,为惯性平台快速精准初始对准提供了一种新的思路。
3 仿 真
3.1 仿真条件
这里假设惯性平台在出厂前已经经过标定补偿且残差为小量。为了充分验证所提方案的适用性,将平台初始姿态角与平台系统参数设置为随机量,其中水平姿态角为在±5°内随机分布,方位角在±180°内随机分布,其余平台误差状态量的均值与标准差大小如表1所示(部分符号定义见文献[19])。
仿真中忽略加速度计杆臂效应和平台稳定回路误差,采样周期为0.1s,加矩指令生成周期为0.1s,滤波周期为0.1s,加速度计输出为速度增量,其测量噪声为0.1μg·s,当量误差为1μg·s,陀螺仪测量噪声为0.001°/h。滤波器姿态角初值为粗对准结果,其余初值设置为零,Q与R根据惯性仪表噪声特性设置,P矩阵设置为对角阵。仿真中所有积分均采用4阶Runge-Kutta积分算法。
3.2 仿真结果与分析
为了充分考核与验证所提方案的有效性,采用蒙特-卡洛(Monte-Carlo,MC)仿真手段,仿真次数为500次,平台姿态角仿真真值如图3~5所示。其中图3和图5为500次MC仿真的水平姿态角真值,图4为500次MC仿真的方位角真值。从图3~5可以看出,平台水平姿态角真值在±5°内随机分布,方位角真值在±180°内随机分布,仿真结果与设计相符。
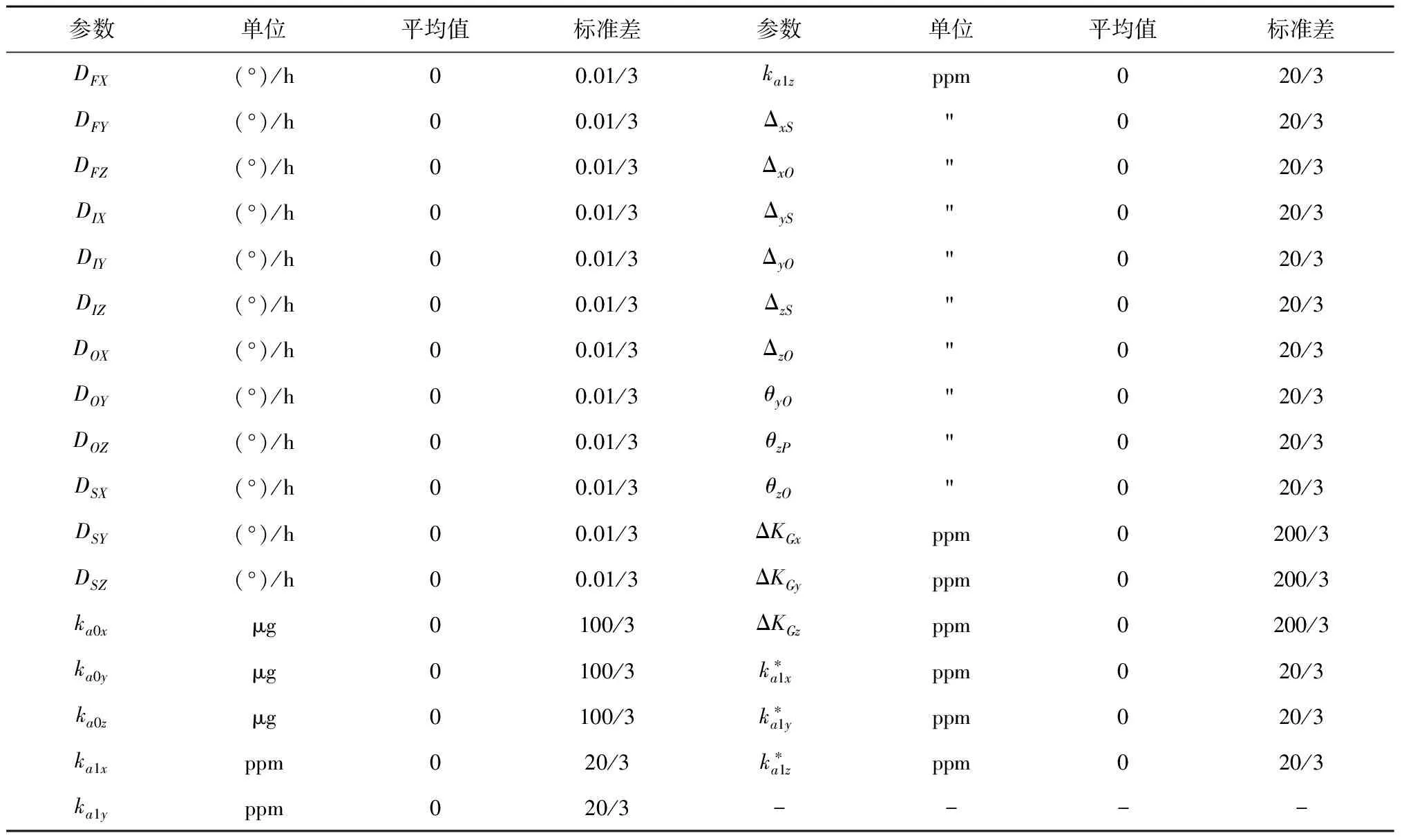
表1 系统状态量初值Table 1 Initial state values and simulation results
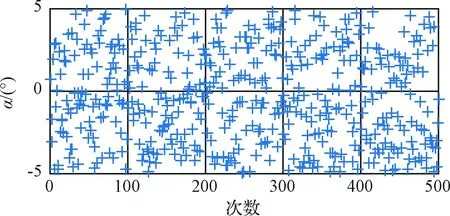
图3 水平姿态角α真值Fig.3 The true value of horizontal angle α
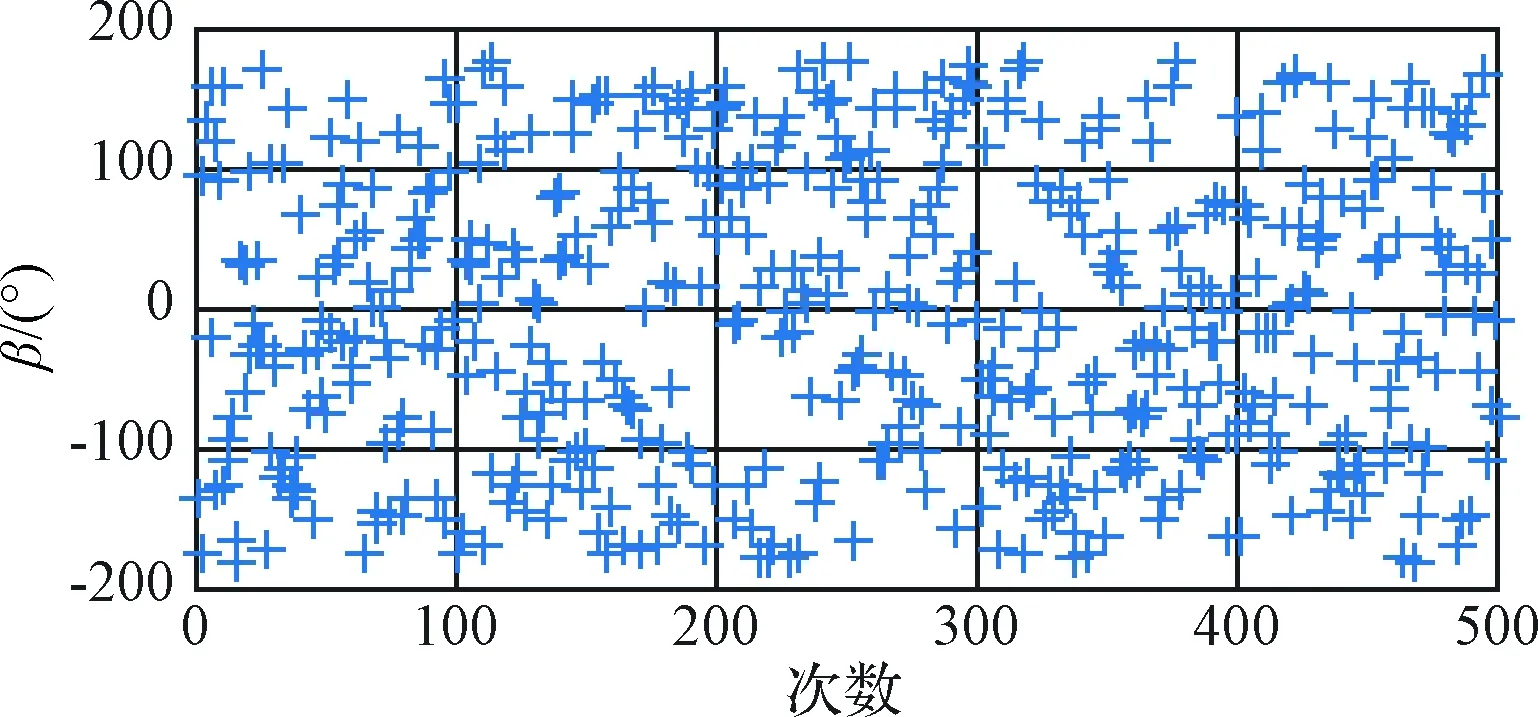
图4 方位姿态角β真值Fig.4 The true value of azimuth angle β
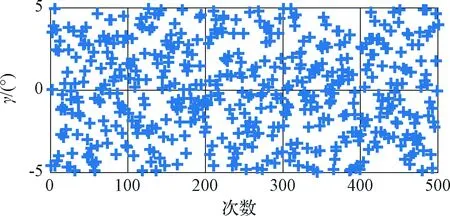
图5 水平姿态角γ真值Fig.5 The true value of horizontal angle γ
利用本文所提的粗对准加精对准方法进行初始对准,其中前60s数据用于粗对准,后720s数据用于精对准,整个初始对准共需13min左右。500次仿真结果如下。
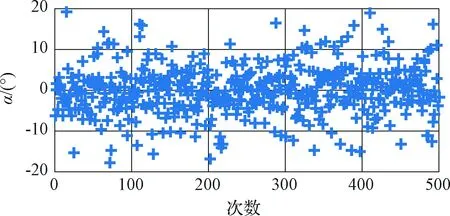
图6 姿态角α粗对准估计偏差Fig.6 The estimated errors of α in coarse alignment

图7 姿态角β粗对准估计偏差Fig.7 The estimated errors of β in coarse alignment
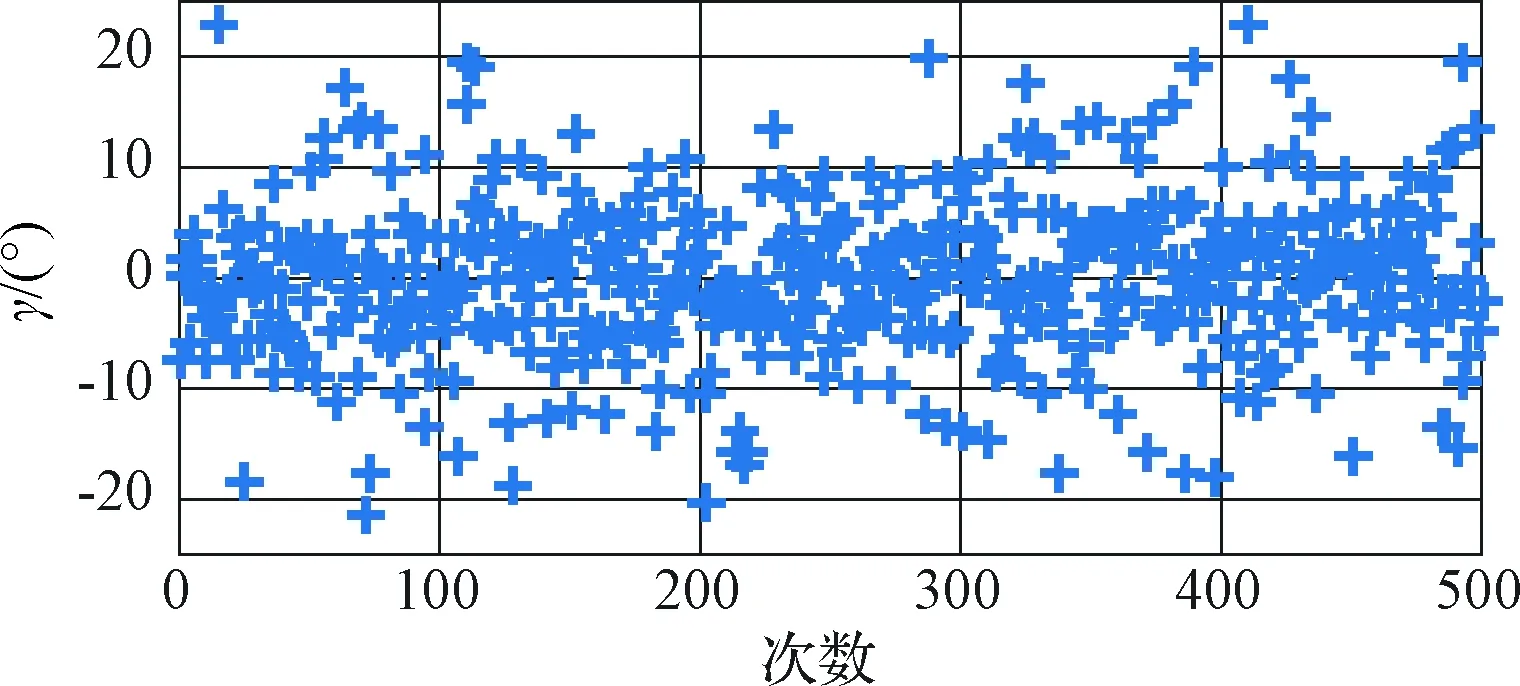
图8 姿态角γ粗对准估计偏差Fig.8 The estimated errors of γ in coarse alignment
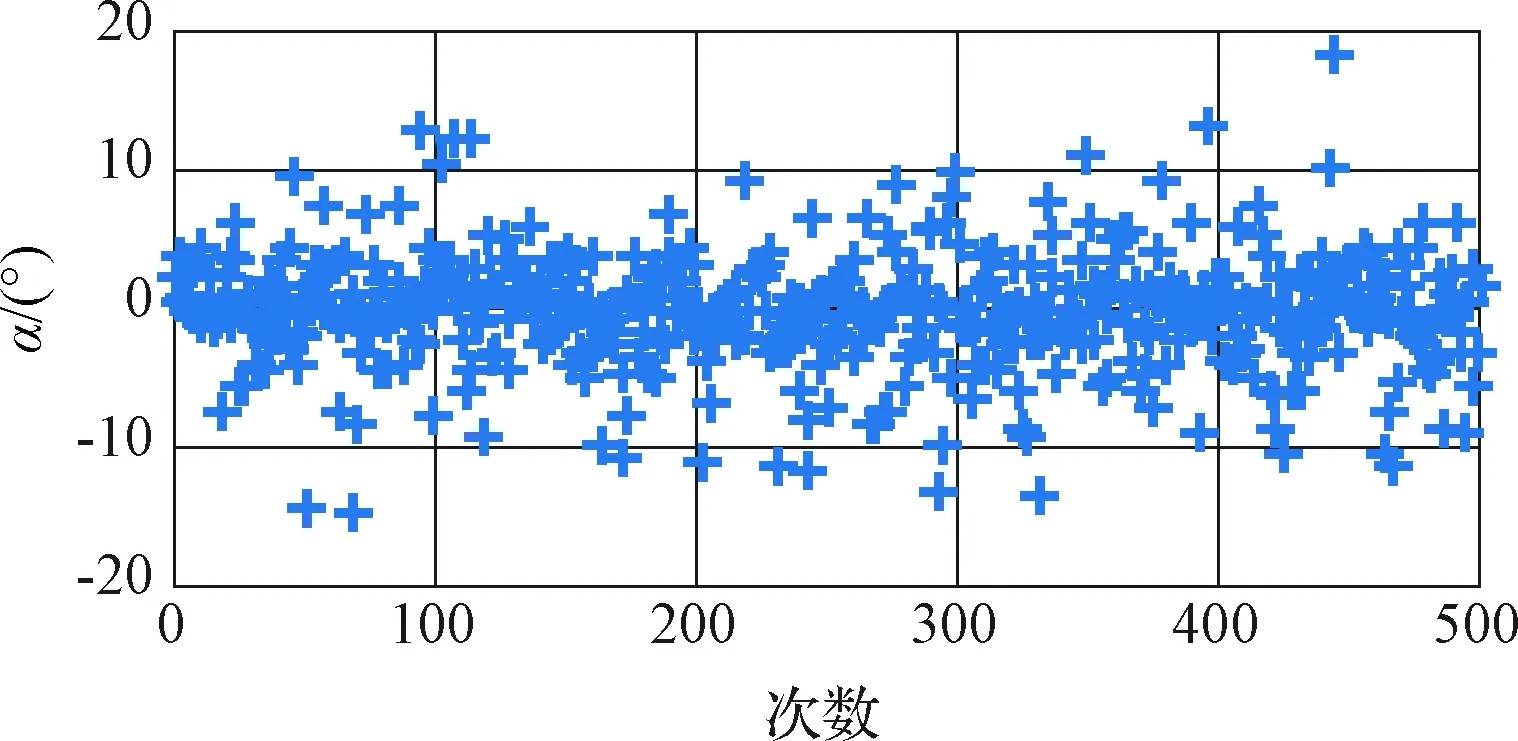
图9 姿态角α精对准估计偏差Fig.9 The estimated errors of α in fine alignment
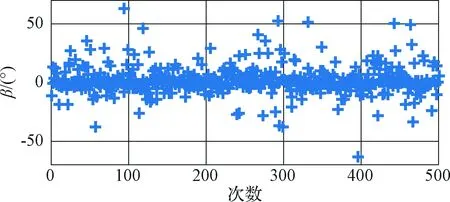
图10 姿态角β精对准估计偏差Fig.10 The estimated errors of β in fine alignment
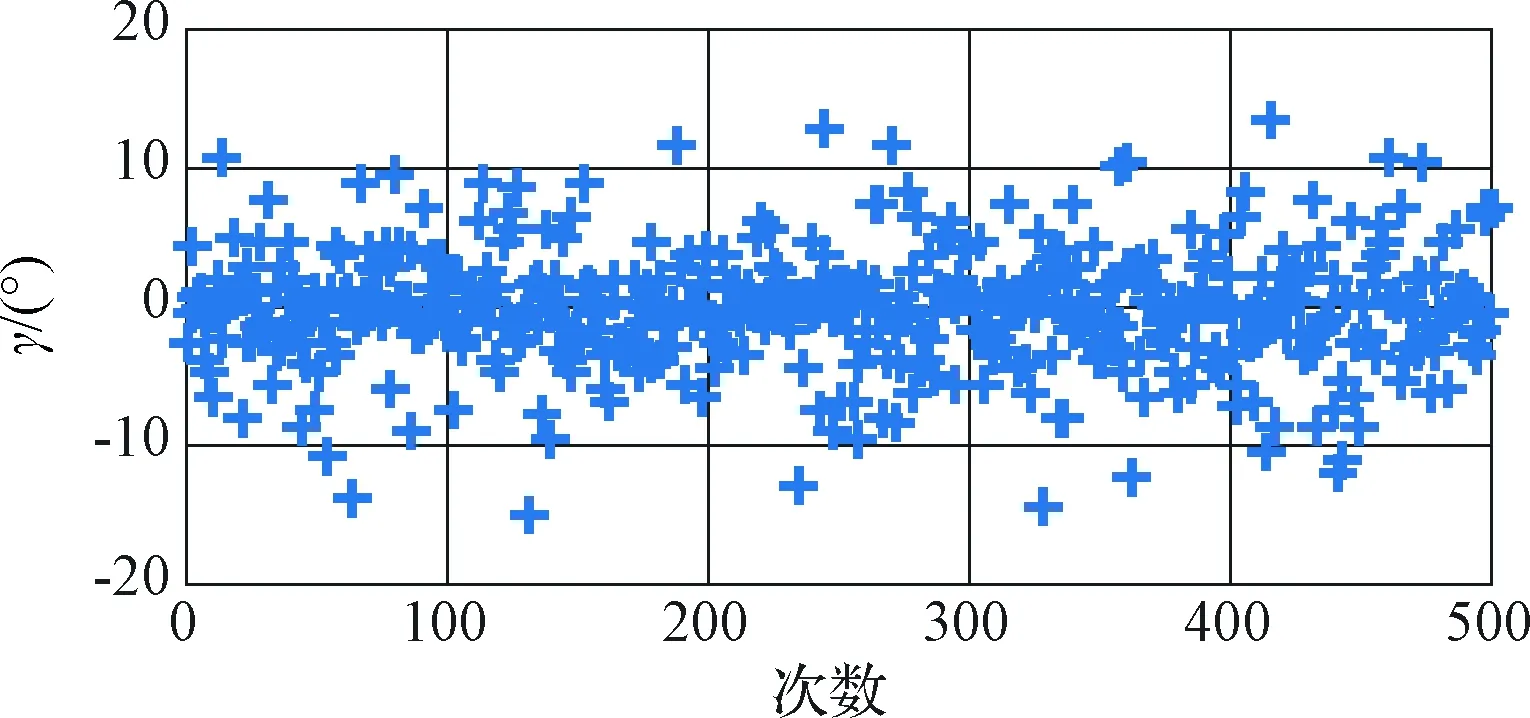
图11 姿态角γ精对准估计偏差Fig.11 The estimated errors of γ in fine alignment
图6~8为粗对准估计偏差。从图6~7可以看出,平台姿态角估计偏差基本服从正态分布,其中水平姿态角最大误差不超过20",方位角最大误差相对于水平姿态角对准误差较大,最大误差超过了200"。上述结果表明了粗对准结果不能满足武器系统要求,尤其是方位角精度较差,这与方位角可观性较差有关,因此,需要通过精对准进一步提高对准精度。
图9~11为500次精对准仿真中姿态角估计偏差结果示意图。从图9~11可以看出,各姿态角估计偏差服从正态分布。与粗对准结果相比,平台水平姿态角最大偏差减小至30"以内,方位角最大偏差降低至90"以内。
为进一步对比分析粗对准和精对准结果,对上述仿真结果进行统计分析,结果如表2所示,其中估计偏差均值与标准差的单位均为角秒。
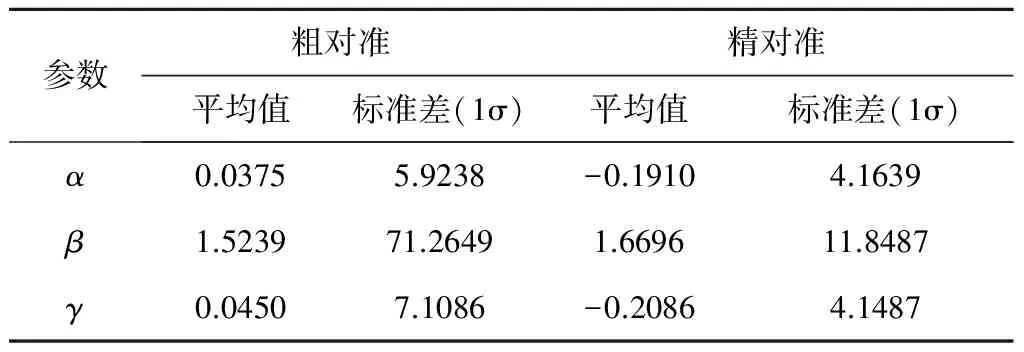
表2 500次仿真的估计偏差Table 2 The estimated errors of 500 simulations
从表2可以看出,经过精对准,粗对准的水平姿态角最大标准差从7.1086"(1σ)降低至6.1639"(1σ),方位角标准差能够从71.2649"(1σ)减少至11.8487"(1σ),有效提高了惯性平台初始对准精度。
4 结 论
针对惯性平台初始自对准问题,本文提出了一种粗对准+精对准的快速初始自对准方法。其中粗对准利用了重力矢量绕地球自转轴旋转的特性,能够在短时间内为精对准提供初值;精对准则采用了Kalman滤波技术,通过加矩方案设计,令平台绕天向轴快速旋转,提高了方位角的可观测度。仿真算例表明,该方法能够在420 s内实现惯性平台初始自对准,其中水平角对准精度优于5"(1σ),方位角对准精度优于12"(1σ),有效地解决了惯性平台初始自对准问题,同时避免了传统方法存在的弊端,提高了惯性平台性能,具有良好的应用前景。
[1] Hanching G W, Thomas C W. High-accuracy inertial stabilized platform for hostile [J]. IEEE Control Systems, 2008, 2: 65-85.
[2] 李安梁, 蔡洪, 白锡斌. 浮球式惯导平台的自适应模糊滑膜稳定控制[J]. 国防科技大学学报, 2013, 35(6): 41-45. [Li An-liang, Cai Hong, Bai Xi-bin. Adaptive fuzzy sliding mode stabilization control for floated inertial platform [J]. Journal of National University of Defense Technology, 2013, 35(6): 41-45.]
[3] Ding Z J, Cai H, Yang H B. An improved multi-position calibration method for low cost micro-electro mechanical systems inertial measurement units [J]. Proc IMechE Part G: J Aerospace Engineering, 2015(10): 1919-1930.
[4] 梅春波, 秦永元, 游金川. SINS 基于非线性量测的大失准角初始对准算法[J]. 宇航学报, 2016, 37(3): 291-297. [Mei Chun-bo, Qin Yong-yuan, You Jin-chuan. Nonlinear measurement based SINS initial alignment algorithm under large misalignment angle [J]. Journal of Astronautics, 2016, 37(3): 291-297.]
[5] 郭泽, 缪玲娟. 基于KF/UKF组合滤波的SINS大方位失准角初始对准[J]. 宇航学报, 2014, 35(2): 163-170. [Guo Ze, Miao Ling-juan. KF/UKF based SINS initial alignment under large azimuth misalignment angle [J]. Journal of Astronautics, 2014, 35(2): 163-170.]
[6] 丁智坚, 蔡洪, 杨华波, 等. 浮球式惯性平台连续翻滚自标定自对准方法[J]. 国防科技大学学报, 2015, 37(3): 148-154. [Ding Zhi-jian, Cai Hong, Yang Hua-bo, et al. Continuous self-calibration and self-alignment method for floated inertial platform [J].Journal of National University of Defense Technology, 2015, 37(3): 148-154.]
[7] 丁智坚, 蔡洪,张文杰. 惯性平台自标定中惯性仪表安装误差可观测性分析[J]. 国防科技大学学报, 2016, 38(5): 127-136. [Ding Zhi-jian, Cai Hong, Zhang Wen-jie. Observability analysis for misalignments of inertial sensors in inertial platform self-calibration [J]. Journal of National University of Defense Technology, 2016, 38(5): 127-136.]
[8] Ding Z J, Cai H, Yang H B. Novel transfer alignment of ship-borne gimbaled inertial navigation systems [J]. Trans. Japan. Society Aeronautic Space Science, 2014, 2: 93-100.
[9] 陆元九. 惯性器件[M]. 北京: 宇航出版社, 1993: 369-437.
[10] 杨华波, 蔡洪, 张士峰. 高精度惯性平台误差自标定方法[J]. 上海航天, 2006, 2: 33-36. [Yang Hua-bo, Cai Hong, Zhang Shi-feng. Calibration for the errors of a high accurate inertial platform [J]. Aerospace Shanghai, 2006, 2: 33-36.]
[11] 杨华波, 蔡洪, 张士峰, 等. 高精度惯性平台连续自标定自对准技术[J]. 宇航学报, 2006, 27(4): 600-604. [Yang Hua-bo, Cai hong, Zhang Shi-feng, et al. Continuous calibration and alignment techniques for a high precision inertial platform [J]. Journal of Astronautics, 2006, 27(4): 600-604.]
[12] 曹渊, 张士峰, 杨华波, 等. 惯导平台误差快速自标定方法研究[J]. 宇航学报, 2011, 32(6): 1281-1287. [Cao Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Research on rapid self-calibration method for inertial platform [J]. Journal of Astronautics, 2011, 32(6): 1281-1287.]
[13] 曹渊, 张士峰, 杨华波, 等. 一种新的惯性平台快速连续旋转自对准方法[J]. 兵工学报, 2011, 32(12): 1468-1473. [Cao Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Fast self-alignment method for inertial platform through continuous rotation [J]. Acta Armamentarll, 2011, 32(12): 1468-1473.]
[14] Cao Y, Cai H, Zhang S F, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit [J]. Measurement Science and Technology, 2012, 23(1): 385-394.
[15] 肖正林, 钱培贤, 徐军辉. 三轴平台快速自标定与自对准方法探讨[J]. 宇航学报, 2006, 27(2): 222-226. [Xiao Zheng-lin, Qian Pei-xian , Xu Jun-hui. Research on rapid auto-calibration and auto-alignment method for three-axis platform [J]. Journal of Astronautics, 2006, 27(2): 222-226.]
[16] Titterton D H, Weston J L. Strapdown inertial navigation technology (2nd Ed) [M]. London, United Kingdom: Peter Peregrinus Ltd. on behalf of the Institute of Electrical Engineers, 2004.
[17] 刘静, 朱志刚. 摇摆条件下惯性平台系统动态特性分析[J]. 宇航学报, 2011, 32(9): 1878-1883. [Liu Jing, Zhu Zhi-gang. Dynamic performance analysis of inertial platform system on rocking base [J]. Journal of Astronautics, 2011, 32(9): 1878-1883.]
[18] 肖正林, 牟建华. 惯性平台动态误差消除方法研究[J]. 宇航学报, 2008, 29(2): 191-194. [Xiao Zheng-lin,Mou Jian-hua. The method to cancel the dynamic level error of inertial navigation platform [J]. Journal of Astronautics, 2008, 29(2): 191-194.]
[19] 秦永元, 严恭敏, 顾冬晴, 等.摇摆基座上基于信息的捷联惯导粗对准研究[J].西北工业大学学报, 2005, 23(5): 681-684. [Qin Yong-yuan, Yan Gong-min, Gu Dong-qing, et al. A clever way of SINS coarse alignment despite rocking ship [J]. Journal of North Western Polytechnical University, 2005, 23(5): 681-684.]
[20] Hellings F J. Application of extended Kalman filtering to a dynamic laboratory calibration of an inertial navigation system [R]. AD 763718: 77-118.
[21] Sifter D J, Henderson V D. An advanced software mechanization for calibration and alignment of the advanced inertial reference sphere [C]. Eighth Guidance Test Symposium, HAFB, New Mexico, USA, May 13-15, 1977.
[22] 万德钧, 房建成. 惯性导航初始对准[M]. 南京:东南大学出版社, 1995:36-45.
通信地址:四川绵阳涪城区二环路南段6号19信箱01分信箱(621000)
电话:17738406202
E-mail: d.sound@163.com
周 欢(1984-),女,博士,工程师,主要从事飞行动力学、导航制导与控制等方向研究。本文通信作者。
通信地址:四川绵阳919信箱411分箱(621900)
电话:(0816)2483263
E-mail: jocelynzhouhuan@163.com
Initial Self-Alignment Method for Inertial Platform on a Stationary Base
DING Zhi-jian1, ZHOU Huan2, ZHANG Shi-feng3, YANG Hua-bo3, CAI Hong3
(1. Air-breathing Hypersonic Research Center, China Aerodynamics Research and Development Center, Mianyang 621000, China;2. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China;3. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
A fast initial self-alignment method is proposed for a gimbal inertial platform system on a stationary base. Firstly, the coarse alignment is accomplished based on the fact that the gravity vector rotates around the Earth′s axis. Further, the platform is rotated along the vertical axis by torqueing command, and then the fine alignment is achieved using the Kalman filter technology and the coarse alignment results. Simulation cases illustrate that the proposed method can align the platform within 460 seconds, the estimated error of the horizontal angles is less than 5" (1σ), and the azimuth angle is less than 13" (1σ). These results show that the proposed approach can significantly improve the response speed and the navigation precision of the system.
Inertial platform; Initial self-calibration; Kalman filter; Stationary base
2016-11-28;
2017-05-13
航天科技创新基金(CASC201105)
V448.12
A
1000-1328(2017)06-0612-09
10.3873/j.issn.1000-1328.2017.06.008
丁智坚(1988-),男,博士,助理研究员,主要从事惯性技术、飞行器设计等方向研究。
