化学镀镍-磷两种动力学模型的比较

陈正平，万丽娟，邹友琴，蒋柏泉,,

（1.南昌大学科技学院生化系，江西 南昌 330029；2.南昌大学资源、环境与化工学院，江西 南昌 330031）

化学镀镍-磷两种动力学模型的比较

陈正平1，万丽娟1，邹友琴2，蒋柏泉1,2,*

（1.南昌大学科技学院生化系，江西 南昌 330029；2.南昌大学资源、环境与化工学院，江西 南昌 330031）

对石英光纤表面化学镀镍-磷的动力学进行了研究。在相同实验范围内，分别建立了幂函数型和多元二次型动力学模型。通过 79个不同因素水平组合所获得的实验数据对两种模型的可靠性进行了比较。结果表明，幂函数动力学模型计算的镀速与实验值相对误差小于5%的有67个，大于5%而小于10%以及大于10%的各有6个，最大相对误差为13.86%；多元二次型动力学模型计算的镀速与实验值相对误差小于5%的有78个，大于5%的只有1个(7.68%)。多元二次动力学模型更可靠。与幂函数动力学模型相比，用Design-Expert 7.00软件中的响应面(Box-Behnken)程序可自动建立多元二次型动力学模型，并判别模型的可靠性及各模型项对镀速影响的显著程度。

镍-磷合金；化学镀；动力学模型；幂函数；多元二次多项式；响应面法；镀速

化学镀是一个自催化的化学反应过程，金属在基体上沉积的速率对镀层的厚度和质量(如表面平整度、光亮度、缺陷数量、致密性、耐蚀性等)有很大的影响。建立化学镀动力学模型(即镀速方程)不仅可预测不同工艺条件下的反应速率，以便选择适宜的工艺参数进行操作，达到所需的镀层厚度和确保镀层的质量，而且可以满足反应过程开发和反应器设计的需要。一般化学反应的动力学模型主要以幂函数或双曲线两种形式表达[1]，而化学镀自催化反应的动力学模型通常以幂函数表示[2-7]。笔者课题组最近通过响应面实验方法建立了化学镀镍-磷-硼的多元二次动力学模型[8]，这是一种新的化学镀动力学模型的表达形式，但未将它与幂函数型动力学模型进行比较，也未见有相关文献报道。本文通过在石英光纤表面化学镀镍-磷动力学的研究，分别建立了幂函数型和多元二次型动力学模型，并对两个模型的可靠性和各自特点进行了分析和比较。

1 实验

1. 1 原材料

石英光纤外径125 μm，保护层厚度25 μm。化学药品见参考文献[9]。

1. 2 设备和仪器

设备和仪器见参考文献[9]。

1. 3 光纤表面预处理

石英光纤表面的预处理见文献[9]。

1. 4 工艺参数

取镀液中硫酸镍浓度(cA)、次磷酸钠浓度(cB)、丙酸浓度(cC)、硼酸浓度(cD)、pH或镀液中氢离子浓度(cE)和镀液温度(热力学温度T或摄氏温度t)作为镀速的影响因素，各因素的实验值范围[9]如下。

水平1 水平2 水平3 水平4 水平5c/ ( m o l / L )： 0 . 0 9 5 1 0 . 1 1 4 1 0 . 1 3 3 2 0 . 1 5 2 2 0 . 1 7 1 2 Ac/ ( m o l / L )： 0 . 1 8 8 7 0 . 2 2 6 4 0 . 2 6 4 2 0 . 3 0 1 9 0 . 3 3 9 6 Bc/ ( m o l / L )： 0 . 1 6 2 2 0 . 2 1 6 2 0 . 2 7 0 3 0 . 3 2 4 3 0 . 3 7 8 4 Cc/ ( m o l / L )： 0 . 3 2 2 6 0 . 3 8 7 1 0 . 4 5 1 6 0 . 5 1 6 1 0 . 5 8 0 6 Dc/ ( × 1 0-3m o l / L ) (或p H )： 1 . 0 ( 3 . 0 ) 0 . 3 1 6 ( 3 . 5 ) 0 . 1 ( 4 . 0 ) 0 . 0 3 1 6 ( 4 . 5 ) 0 . 0 0 1 ( 5 . 0 )T/ K (或t/ ° C )： 3 5 5 . 5 ( 8 2 . 5 ) 3 5 7 . 0 ( 8 4 . 0 ) 3 5 8 . 5 ( 8 5 . 5 ) 3 6 0 . 0 ( 8 7 . 0 ) 3 6 1 . 5 ( 8 8 . 5 ) E

1. 5 镀速的测定

采用称重法测定镀速：取10 cm长的裸光纤，施镀前先称其质量(m1)，施镀结束后再称裸光纤和镀层的总质量(m2)，根据m1和m2计算出镀层质量，换算成物质的量后计算出镀速v[单位为mol/(cm·min)]。

1. 6 幂函数型动力学模型实验方法

将化学镀镍-磷幂函数型动力学模型的表达式[10]如下：

两边取对数，得

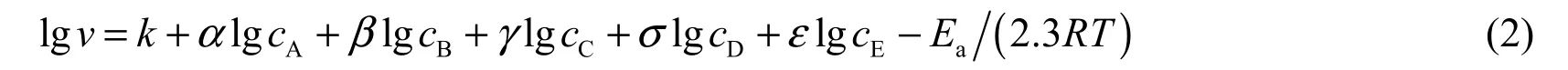
式中：Ea为反应活化能，J/mol；R为气体常数，8.314 J/(mol·K)。

分别固定式(2)中任意5个因素的水平，试验考察某一因素水平对镀速的影响，并通过作图lgv-lgcA，lgv-lgcB，lgv-lgcC，lgv-lgcD，lgv-lgcE和lgv-1/T，分别获得各斜率α、β、γ、σ、ε和Ea，将它们代入式(1)，再求出反应速率常数k，即可得到幂函数型动力学模型。

1. 7 多元二次型动力学模型实验方法

采用响应面试验法建立化学镀镍-磷的多元二次型动力学模型。根据1.4节的工艺参数范围，设计和编制响应面试验的因素、水平和编码，如表1所示。

表1 化学镀镍-磷响应面试验因素、水平和编码Table 1 Factors, levels, and codes of response surface test

将表1中的数据输入到Design-Expert 7.00软件中的Response Surface(Box-Behnken)程序中，可设计出54个试验点(其中6个是相同水平组合的中心点，故共49个不同水平的试验点)，根据各试验点进行试验，并把实验数据代入程序进行回归拟合，自动输出化学镀镍-磷的多元二次型动力学模型。

2 结果与讨论

2. 1 幂函数型动力学模型

按照1.6节，建立的化学镀镍-磷幂函数型动力学模型为：

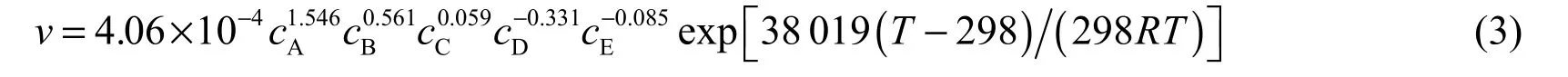
式中k的单位为L1.704/(mol0.704·cm·min)。

用于建立幂函数型动力学模型的30个试验点的试验值和模型计算值列于表2。

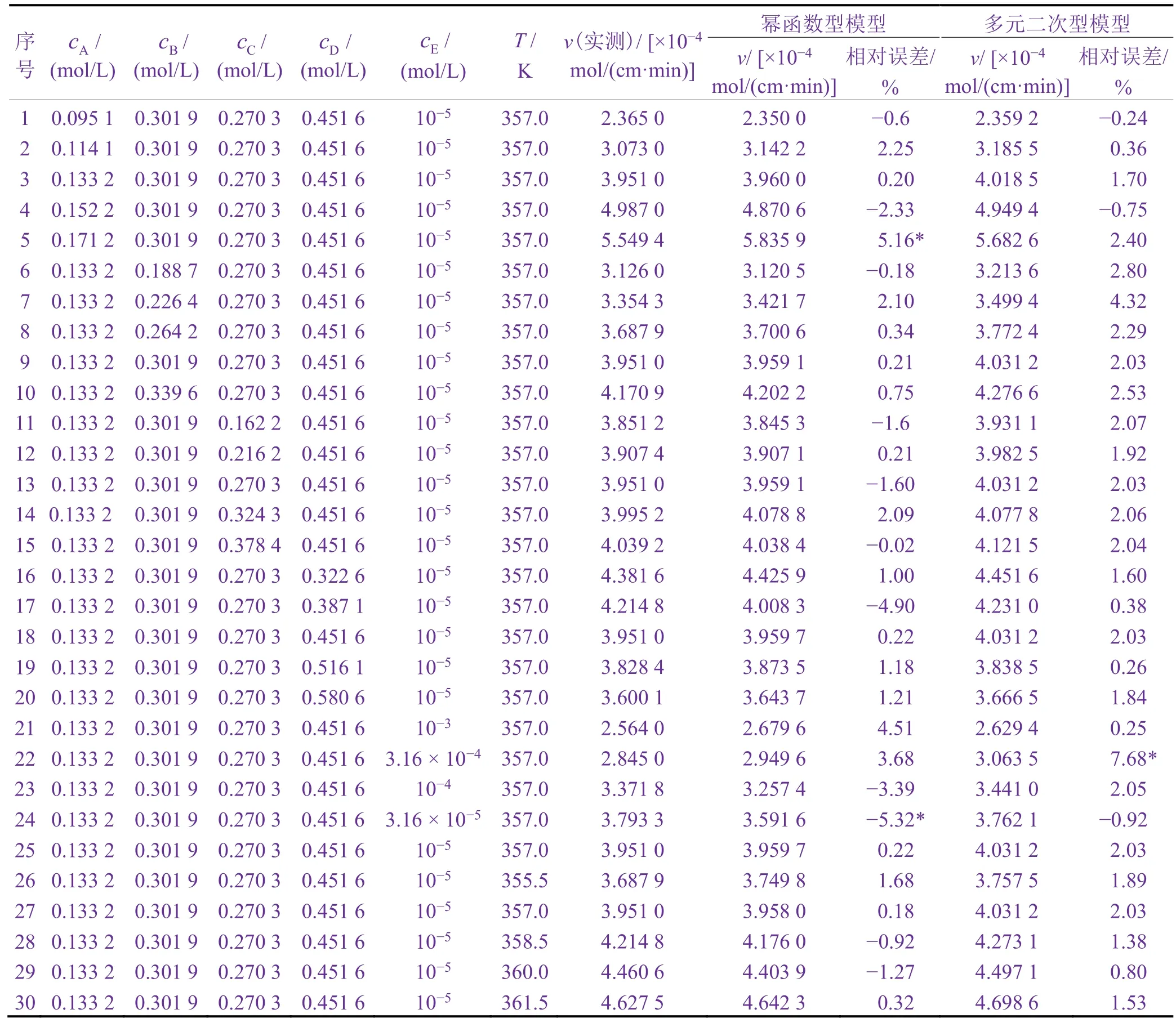
表2 不同工艺条件下幂函数型动力学模型计算的镀速和试验值Table 2 Deposition rates calculated by power function kinetic model and the tested values under different process conditions

由表2可见，30个试验点的模型计算值与试验值的相对误差中，绝对值小于1%的有13个(占43.3%)，介于1%与5%之间的有15个(占50%)，大于5%(右上角带*号)的有2个(占6.7%)，说明建立的化学镀镍-磷幂函数型动力学模型与试验结果有较好的吻合度，较为可靠。

2. 2 多元二次型动力学模型

根据1.7节的方法，由Design-Expert 7.00软件的Response Surface(Box-Behnken)程序自动拟合的化学镀镍-磷多元二次型动力学模型表示如下：

用于建立多元二次型动力学模型的54个试验点的试验值和模型计算值列于表3。

表3 不同工艺条件下多元二次型动力学模型计算的镀速与试验值和幂函数型动力学模型计算值的对比Table 3 Deposition rates calculated by multivariate quadratic kinetic model and their comparison with those calculated by power function kinetic model and the tested values under different process conditions

续表3 不同工艺条件下多元二次型动力学模型计算的镀速与试验值和幂函数型动力学模型计算值的对比Table 3 (continued) Deposition rates calculated by multivariate quadratic kinetic model and their comparison with those calculated by power function kinetic model and the tested values under different process conditions

由表3可见，49个不同试验点的模型计算值与试验值的相对误差绝对值均小于5%，其中小于1%的有43个(占比87.8%)，说明建立的多元二次型动力学模型与试验结果的吻合度非常高，该模型十分可靠。

2. 3 两种动力学模型的比较

2. 3. 1 模型的可靠性

将多元二次型动力学模型的49个试验点的参数值分别代入幂函数型动力学模型，计算值和试验值的相对误差值见表3。相对误差绝对值小于1%的有14个(占28.6%)，介于1%和5%之间的有25个(占51.0%)，大于5%的(右上角带*号)有4个(占8.2%)，大于10%的(右上角带**号)的有6个(占12.2%)，其中最大的是 13.86%。可见幂函数型动力学模型的计算值与该 49个试验点的试验值的吻合度不够高，该模型的可靠性较差。

将建立幂函数型动力学模型所用的30个试验点的参数值代入多元二次型动力学模型，计算值与试验值的相对误差见表2。相对误差绝对值小于1%的有8个(占26.7%)，介于1%和5%之间的有21个(占70.0%)，大于5%(右上角带*号)的只有1个(占3.3%)。这说明多元二次型动力学模型的计算值与该30个试验点的试验值也有较好的吻合度，该模型较为可靠。

2. 3. 2 方程的特点

建立化学镀镍-磷幂函数型动力学模型时，镀液中各组分用量以浓度(mol/L)表示，pH应转换成镀液中的氢离子浓度(可按pH = -lgcH+计算)，温度单位为K，金属沉积量以物质的量(单位为mol)来表示。模型的可靠性主要根据试验值与模型计算值的相对误差来判断，各因素对镀速影响的显著程度无法判断。模型中的常数必须通过手算或编程计算才能获得。

建立化学镀镍-磷多元二次型动力学模型时，镀液中各组分用量以浓度或质量浓度表示均可，pH不必转换成氢离子浓度，温度的单位可用K或°C。各因素采用不同单位时，方程中各常数不同，镀速的单位也不同。如要与幂函数型模型比较，则镀液组分用量、温度和镀速的单位应与幂函数型模型一致。化学镀镍-磷多元二次型动力学模型及其各模型项的可靠性通过它们的显著性来判断，而显著性可由程序给出的F和P值来确定，见表4。

当P(Prob ＞ F )≤0.01、0.01≤P(Prob ＞ F )≤0.05、0.05≤P(Prob ＞ F )≤0.1和P(Prob ＞ F )≥0.1时，它们对镀速的影响程度分别为极其显著、显著、有一定影响和无影响。P(Prob ＞ F )值越小，对镀速的影响越显著。P(Prob ＞ F )值相同时，F值越大，显著性越强。

根据上述原则，可知本文所建立的多元二次型动力学模型是极其显著的，可靠性很高，这与通过试验值和模型计算值之间的相对误差来判断所得到的结果是一致的。多元二次型动力学模型中的各项对镀速影响的显著程度也可根据表4中的P(Prob ＞ F )和F值来判断。

3 结论

在相同试验范围内分别建立了化学镀镍-磷幂函数型动力学模型和多元二次型动力学模型，并通过79组试验数据对这两种模型进行验证。前者的计算值与试验值的相对误差的绝对值小于5%的有67个，大于5%的有4个，大于10%的有6个，最大值为13.86%；后者的计算值与试验值的相对误差的绝对值小于5%的有78个，大于5%的只有1个(7.68%)。由此可见，本例中的化学镀镍-磷多元二次型动力学模型与试验结果的吻合程度比幂函数型动力学模型更好，可靠性更高。多元二次型动力学模型及其模型项的显著程度可直接由软件程序识别，而幂函数型动力学模型则无法判断。

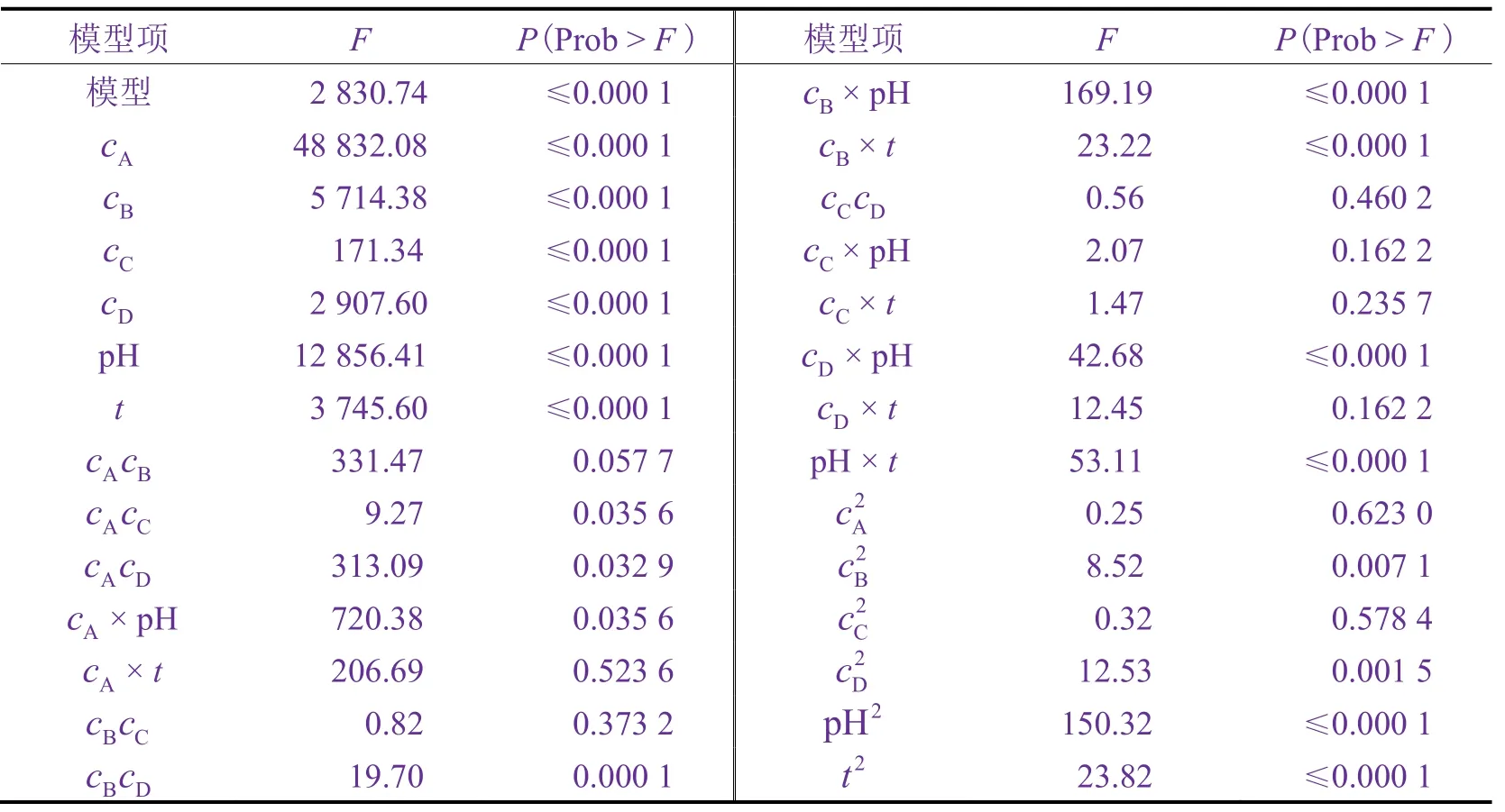
表4 多元二次型动力学模型及其各项的F和P值Table 4 F and P values of multivariate quadratic kinetic model and its terms

[1] 朱丙辰. 化学反应工程[M]. 5版. 北京： 化学工业出版社, 2012： 9-10.

[2] 李宁. 化学镀实用技术[M]. 2版. 北京： 化学工业出版社, 2012： 44.

[3] 郭敏, 郑玉峰. 化学镀制备碳负载型多孔钯及其动力学研究[J]. 材料导报, 2013, 27 (4)： 56-59.

[4] 周英智, 刘峥, 张京迪. 涤纶织物上化学镀铜镍合金的动力学研究[J]. 电镀与涂饰, 2012, 31 (5)： 30-33.

[5] 李忠, 王丽娜, 王桂雪, 等. 负载型Ni-Co-P/CNFs催化剂的制备及释氢性能[J]. 燃料化学学报, 2015, 43 (3)： 372-378.

[6] 闫操, 戴玉林, 徐宏, 等. Fe粉表面化学镀Ni-P的热力学与动力学[J]. 化学工程, 2011, 39 (1)： 73-76, 97.

[7] 杨余芳, 衷明华, 黄俊生. 化学镀锡反应动力学特性研究[J]. 表面技术, 2014, 43 (6)： 64-68.

[8] 刘停, 李敏, 蒋柏泉, 等. 化学镀镍-磷-硼自催化反应多元二次回归动力学方程研究[J]. 电镀与涂饰, 2015, 34 (20)： 1155-1159.

[9] 蒋柏泉, 李春, 白立晓, 等. 石英光纤表面化学镀Ni-P的工艺研究及其表征[J]. 南昌大学学报(工科版), 2008, 30 (3)： 205-208.

[10] 蒋柏泉, 肖琳, 彭健, 等. 石英光纤表面化学镀Ni-P-B工艺及其动力学[J]. 南昌大学学报(理科版), 2008, 32 (5)： 452-456.

[ 编辑：温靖邦 ]

Comparison between two kinetic models for electroless nickel-phosphorous deposition

CHEN Zheng-ping, WAN Li-juan, ZOU You-qin, JIANG Bo-quan*

The kinetic study on electroless Ni-P deposition on the surface of quartz optical fiber was carried out. A power function model and a multivariate quadratic model were separately established within the same experimental range. The reliability of the two models were compared based on 79 groups of the combinations of different factors at different levels. The results showed that the number of relative errors between the deposition rates calculated by the power function model and experimental values is 67 for ＜5%, 6 for 5%-10% and 6 for ＞10%, and the maximum relative error is 13.86%. The relative errors of the multivariate quadratic model are all less than 5% except that one is 7.86%. The multivariate quadratic model is more reliable than the power function model. As compared with the power function kinetic model, the multivariate quadratic model can be established automatically by using response surface (Box-Behnken) program in Design-Expert 7.00 software, and its reliability and the significance of the effect of individual term on deposition rate identified.

nickel-phosphorous alloy; electroless plating; kinetic model; power function; multivariate quadratic polynomial; response surface methodology; deposition rate

Department of Biology and Chemistry, College of Science and Technology, Nanchang University, Nanchang 330029, China

TQ153.2

A

1004 - 227X (2017) 12 - 0617 - 06

10.19289/j.1004-227x.2017.12.002

2017-02-28

2017-04-07

江西省重大科研专项计划（20124ABE02104）。

陈正平（1962-），男，江西进贤人，副教授，主要从事电化学研究。

蒋柏泉，教授，(E-mail) jbq_win@163.com。