关于大学物理中电势、场强微分关系教学的一点讨论

何 健

(绵阳师范学院数理学院,四川 绵阳 621000)



关于大学物理中电势、场强微分关系教学的一点讨论

何 健

(绵阳师范学院数理学院,四川 绵阳 621000)

目前大学物理教学中关于电势、场强微分关系的讨论主要是借助场线与等势面的几何关系，从方向导数入手进行的。这一方法直观性好，但不够深刻，尤其针对诸如“法线”“方向导数”等概念的刻画较为模糊。本文尝试直接通过全微分导出电势与场强关系的直角坐标表示，在此过程中遇到一些细节问题，例如“难以直接获得关于法线方向的表示”等。通过分析造成困难的原因，指出关键点在于如何牢牢抓住“法向基矢n的实质就是一长度为1的有向线段”这一问题，引入其首尾两点坐标，将其表示细化，进而给出完整证明，并对教学进行了一些反思。

梯度；方向导数；全微分；电势；电场强度

目前，无论是物理专业的《电磁学》教学，还是《大学物理》的电磁学部分教学中，关于静电场的电场强度(下简称场强)与电势的微分关系的讲解中，几乎都是清一色从方向导数入手，借助场线与等势面的几何关系，最后给出电势梯度在三维直角坐标系中的表达。这样的方法避免了繁杂的运算，从“讲原理，重物理”这个层面上来讲，无可厚非。但同时也会带来一些问题，比如：教学中，老师鼓励学生的发散性思维，支持学生运用所学知识进行一些实际演练，这样会有一部分同学尝试着从梯度的方向导数表示直接通过全微分给出经典的直角坐标表示，而在此过程中，遇到了一些问题，笔者认为有必要把这些问题整理出来与大家共同探讨。

1 经典的操作方法

静电场中电场强度E与电势U的积分关系式为[1]

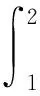
(1)

设任意静电场中，取两个十分邻近的等势面1和2，电势分别为U,U+dU,并设dU>0。则，当一正试探电荷q0从等势面1上的P1点沿dl到达等势面2上的P2点(图1所示)时，电场力做功为:dA=q0(U1-U2)=q0[U-(U+dU)]=-q0dU；而由式(1)，这个功又可以写作

q0E·dl=q0Ecosφdl

(2)

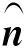
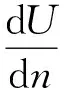
(3)

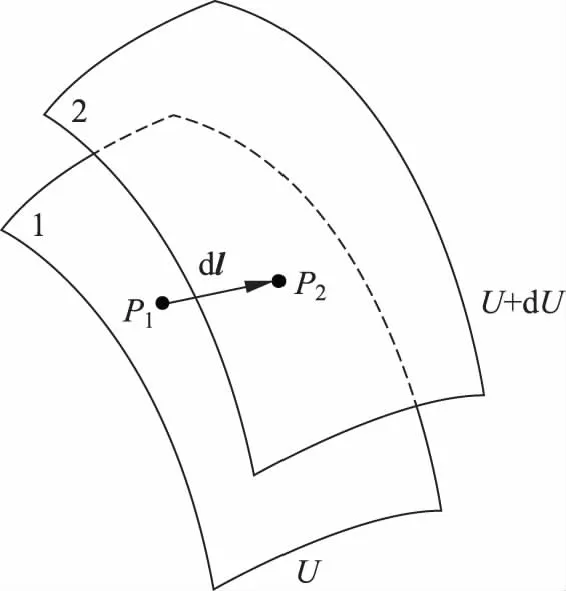
图1 电场力做功示意图

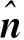
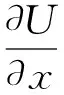
(4)

故，直角坐标系中电场强度E可写成[3]

(5)

以上是目前《大学物理》及《电磁学》教材中比较普遍的推导方法。

2 全微分表示的直接推导法

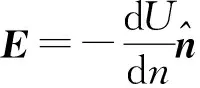
(6)

由此可得

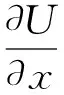
故

(7)

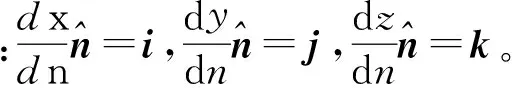
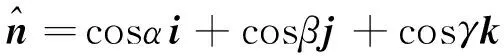
(8)

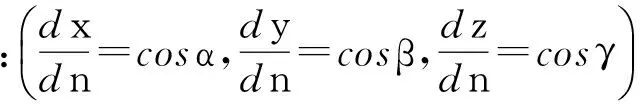
(9)

到此我们当然希望能够通过方向余弦公式cos2α+cos2β+cos2γ=1化简上式以得出最终表达式(5)，然而计算结果却得到如下复杂表示

显然与预期结果相去甚远，这不禁让人感到有些奇怪，按理说这样的结论无论实验还是理论都是非常成功的，但是当我们换一条道路走时，却困难重重，这是为什么呢？

我们尝试从矢量的特性出发，再回到式(7)，将矢量标积拆分还原，得

(10)

再由式(9)，可得

(11)

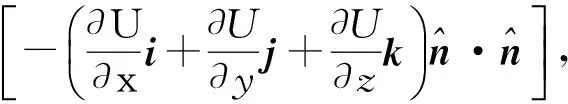
(A×B)×C=(C·A)B-(C·B)A

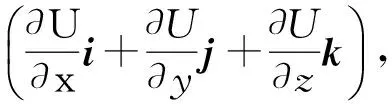
条件是

(12)

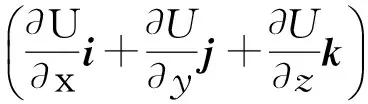
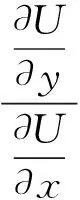
(13)

下面以第一个等式为例给出证明。显然，由于x并非y的函数(彼此独立)，直接求这样的偏导数无意义，可以尝试化为

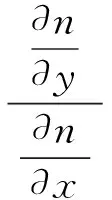
(14)

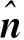
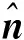
=(x2-x1)i+(y2-y1)j+(z2-z1)k

(15)

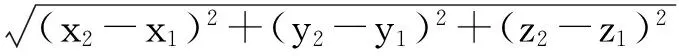
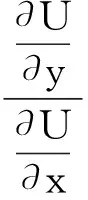
(16)

3 思考与启示

问题至此已告一段落，给我们的思考却很多：

2) 电磁学中对于法线方向与梯度方向关系来历的描述总是模棱两可，一般会用语言表达“……电势梯度，在方向上与等势面法线方向相同……”但是关于其本源，内在联系往往讲解含混，容易造成理解不畅。这些也都反映出作者在撰写教材时的一些想法：不希望将物理教材写得太过数学化，用较少的数学讲明白物理；其初衷是好的，但是也不能忘记：数学的语言是最简洁最有力最不易犯错的，很多时候遇到容易混淆的概念时，将其数学化反而更好。

3) 本文是从电场强度的矢量表达入手，分析得出证明关键式(13)，另外也可让学生从电场强度大小(标量)与电势关系入手进行讨论，给出结论并进行对比分析。

[1] 赵凯华,陈熙谋.电磁学上册[M].2版.北京：高等教育出版社,1998:89-91.

[2] 程守洙，江之永.普通物理学上册[M].6版.北京：高等教育出版社,2006:280-281.

[3] 贾秀敏.均匀带电圆环片的空间静电场[J].大学物理,2010(08):29-30. Jia Xiumin. Space electrostatic field of evenly-charged round ring[J] .College Physics, 2010, 29(8): 29-30. (in Chinese)

■

A DISCUSSION ON THE TEACHING OF THE DIFFERENTIAL RELATIONSHIP BETWEEN ELECTRIC POTENTIAL AND ELECTRIC FIELD STRENGTH IN COLLEGE PHYSICS

He Jian

(School of Physics and Electronics Engineering, Mianyang Normal University, Mianyang Sichuan 621000)

The current discussion on the differential relationship between the Electric potential and the field strength is carrying out by means of the geometric relations between the field line and the potential surface and Starting with the directional derivative. This method is intuitive, but it is not deep enough, especially the description of the concepts such as “normal” and “directional derivative” is relatively Ambiguous. In this paper, we try to directly express the relationship between the electric potential and the field strength by means of the total derivative. In this process, Some of the details encountered, such as “it is difficult to get the representation of the normal direction directly”. By analyzing the cause of the problem, we find the key point that “The essence of normal basis vector is a directed line segment with a length of 1”, introduce both the two coordinates, represent the refinement, and then give a complete proof. Finally, we have some reflection on the teaching.

gradient vector; directional derivative; total differential; electric potential; field strength

2016-04-01

绵阳师范学院2016年科研启动课题，编号：QD2016A002。

何健，男，讲师，主要从事物理教学科研工作,研究方向为光学、大学物理教学论，27992598@qq.com。

何健. 关于大学物理中电势、场强微分关系教学的一点讨论[J]. 物理与工程，2017，27(3)：63-66.