一种基于改进形状分析的黏滞特性检测方法研究

孔杰，田学民，尚林源

(中国石油大学(华东) 信息与控制工程学院，山东 青岛 266580)

一种基于改进形状分析的黏滞特性检测方法研究

孔杰，田学民，尚林源

(中国石油大学(华东) 信息与控制工程学院，山东 青岛 266580)

调节阀黏滞特性是导致工业过程中控制回路振荡的主要原因之一。现有的调节阀黏滞特性检测方法大多都以特定假设为前提，只适用于特定的范围。针对面积峰值法仅适用于自衡对象的限制，提出了一种改进的形状分析法，基于自衡对象和积分对象回路输出形状的差异，对振荡回路偏差信号的二阶导数信号与原信号的较大差异性进行区分，从而进行黏滞特性检测。该方法克服了面积峰值法只适用于特定范围的局限性，通过仿真研究验证了该方法的有效性。

黏滞特性 振荡诊断 调节阀 非线性特性

回路振荡是过程工业中常见的现象，据统计约33%的控制回路处于振荡状态中[1]，该现象会直接导致控制性能变差、产品质量降低、能源的损耗增大等问题产生[2]。

引起控制回路产生振荡现象的原因主要包括： 控制器参数整定不当、阀门黏滞和外部周期性干扰[3]。研究表明[4]： 有20%～30%的回路振荡是由调节阀引起的，调节阀死区、饱和以及黏滞等非线性特性都会不同程度地影响控制回路性能，其中尤以调节阀黏滞特性最为常见。因此，研究调节阀黏滞特性，对石油化工等工业过程安全、稳定、高效的生产有着非常重要的意义。

近年来，关于调节阀黏滞特性检测的研究成果不断涌现，Capaci和Scali[5]对黏滞特性检测方法进行了综述。张波[6]将这些方法分为四大类： 基于互相关函数法，基于形状分析法，基于非线性检测法以及基于模型的算法[7-10]。基于形状分析算法主要包括基于OP-MV形状分析法[11-12]、面积峰值法[13]和曲线拟合法[14-15]；基于非线性检测算法主要有双相干法[16]和替代数据分析法[17]。

Horch[18]提出了利用控制器输出信号与过程输出信号的互相关函数的奇偶性来判断黏滞存在情况，但此方法仅适用于PI控制器下的非积分过程。Rossi&Scali[14]提出了曲线拟合法，通过拟合回路中第一个积分环节后的变量信号，分别比较与正弦信号和三角信号的拟合度，判断是否存在调节阀黏滞特性。双相干方法对信号中非稳态缓慢变化的趋势非常敏感，需要进行维纳滤波；替代数据分析法[17]至少需要12个周期数据并且对非末端匹配数据非常敏感，原则上结合椭圆拟合法也可用于黏滞检测。Daneshwar和Noh[19]提出了基于模糊聚类的方法进行黏滞特性检测，仅应用于流量控制系统。基于OP-MV形状分析法[11-12]是利用控制器输出OP和阀门输出MV之间的关系所绘制二维图的形状来判断黏滞特性，该类方法容易理解、执行简单，但需要得到阀门输出MV信号，应用范围受到限制。面积峰值法通过计算回路偏差信号过零点间峰值前后的面积比值来判断回路中是否存在黏滞特性，该方法需要对过零点和峰值检测，只适用于自衡对象。

目前，调节阀黏滞检测方法比较多，通常都是以特定的假设为前提，因而只适用于特定的范围。针对面积峰值法仅适用于自衡对象的限制，笔者对其进行了改进，使其可适用于自衡对象和积分对象，同时能够更高效地进行黏滞特性检测，通过仿真研究验证了该方法的有效性。

1 调节阀黏滞特性

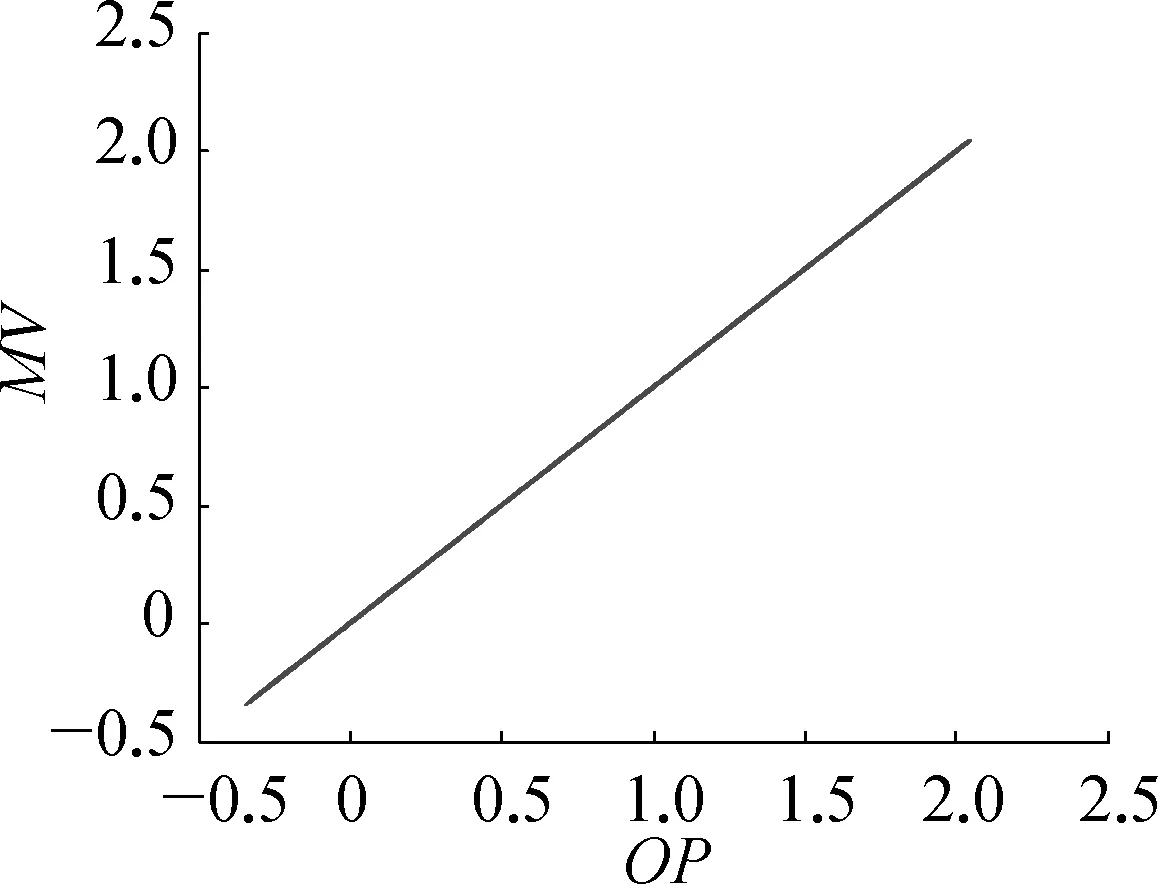
调节阀常见的非线性特性主要有死区、饱和、黏滞等，其中黏滞特性又最为常见，如图1所示，图中OP是控制器输出信号，MV是调节阀输出信号，S表示死区(AB段)加黏性区(BC段)参数，J表示滑动跳跃(CD段)参数。

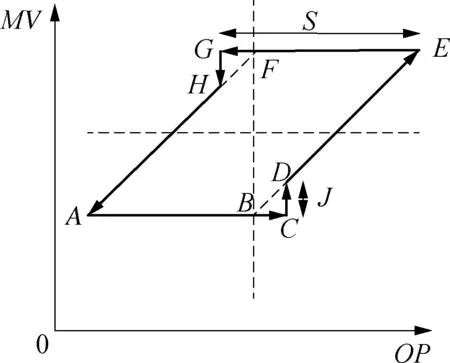
图1 典型阀门黏滞特性示意

图1中，当阀门黏滞引起回路振荡时，黏性阀门的运动可以明确地划分为四个阶段： 死区阶段(AB段)，黏性阶段(BC段)，滑动跳跃阶段(CD段)和连续运动阶段(DE段)。

假设阀门初始位于A点，同时闭环回路稳定运行，由于负载扰动的存在，使得回路产生控制偏差时，控制器输出OP开始增加。如果OP信号不在阀门能够响应的输入范围之内，阀门由A点进入死区阶段，MV不会随着OP的增大而运动，也不会积累势能。OP信号继续增大，并在B点进入有效输入范围之内，此时阀门由死区阶段过渡到黏性阶段，阀门能够感觉到OP的控制作用，但由于OP所产生的作用力小于静摩擦力，阀门无法对控制作用做出响应，因而虽然会积累势能，但仍然会保持静止状态。当到达C点时，OP产生的作用力超过了静摩擦力，阀门进入滑动跳跃阶段，阀门位置突然变化。由D到E是阀门的连续运动阶段，此时阀门位置会随着OP的增大而连续滑动，产生控制作用，减小控制偏差。当偏差减小到一定程度，OP开始减小，此时阀门试图反向运动，但这种运动趋势再次被摩擦力阻止，阀门由E点再次进入黏性阶段，并重复上述的运动过程，最终回路发生振荡。

2 基于改进形状分析的黏滞特性检测方法

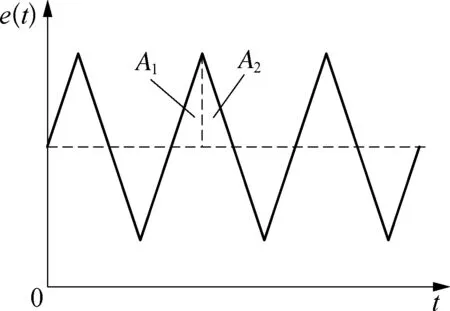
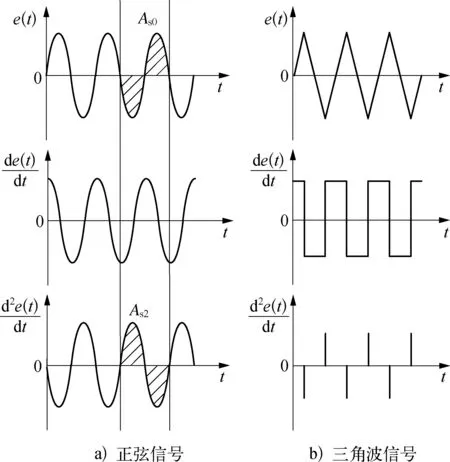
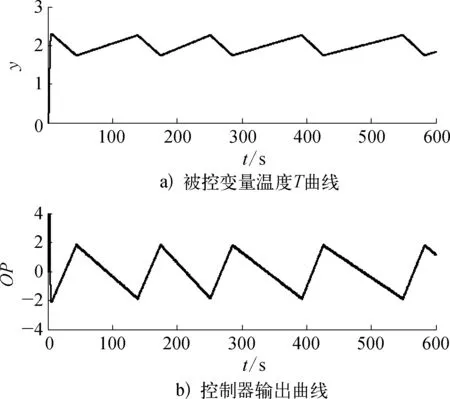
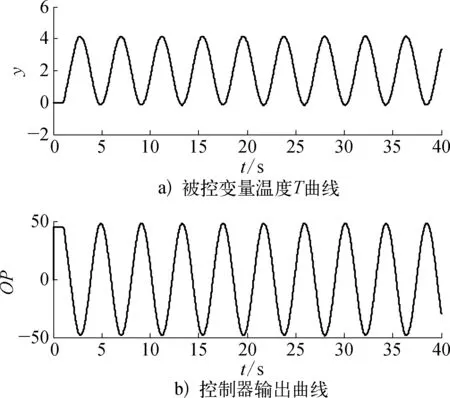
研究表明： 不同原因导致的控制回路振荡，过程输出的偏差信号也不同。在调节阀黏滞特性的作用下，自衡对象的偏差信号表现为近似方波信号，如图2所示；对于有积分作用的非自衡对象，偏差信号表现为三角波信号，如图3所示；由控制器参数整定不当导致的振荡，偏差信号表现为正弦波信号，如图4所示。

对于自衡对象，有黏滞特性的控制回路波形具有不对称性，如图2所示，文献[13]针对这个性质提出了峰值前后面积比较的指标R：

(1)

式中：A1——峰值与峰值前过零点之间的曲线与横轴围成的面积；A2——峰值与峰值后过零点之间的曲线与横轴围成的面积，通过R的大小来判断是否存在黏滞特性。如果比值大于1则表明控制回路波形不对称即回路中存在黏滞特性；如果约等于1表明不存在黏滞特性。判断规则如下，记为规则一：

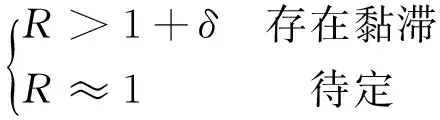
(2)

式中：δ——阈值，它的大小取决于黏滞特性检测方法的灵敏性。δ值越小，对检测方法灵敏性要求越高，同时判断结果的准确率也会降低；反之，δ值越大，则对检测方法灵敏性要求越低，判断结果的准确率会增加。为了更好地权衡两者之间的关系，δ的值通常取0.5～1.0[13]。

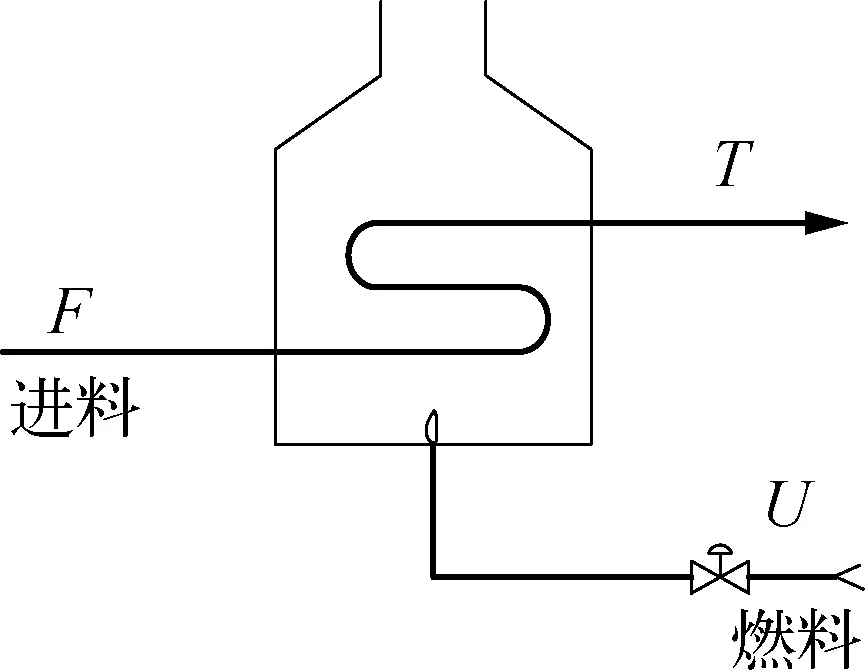
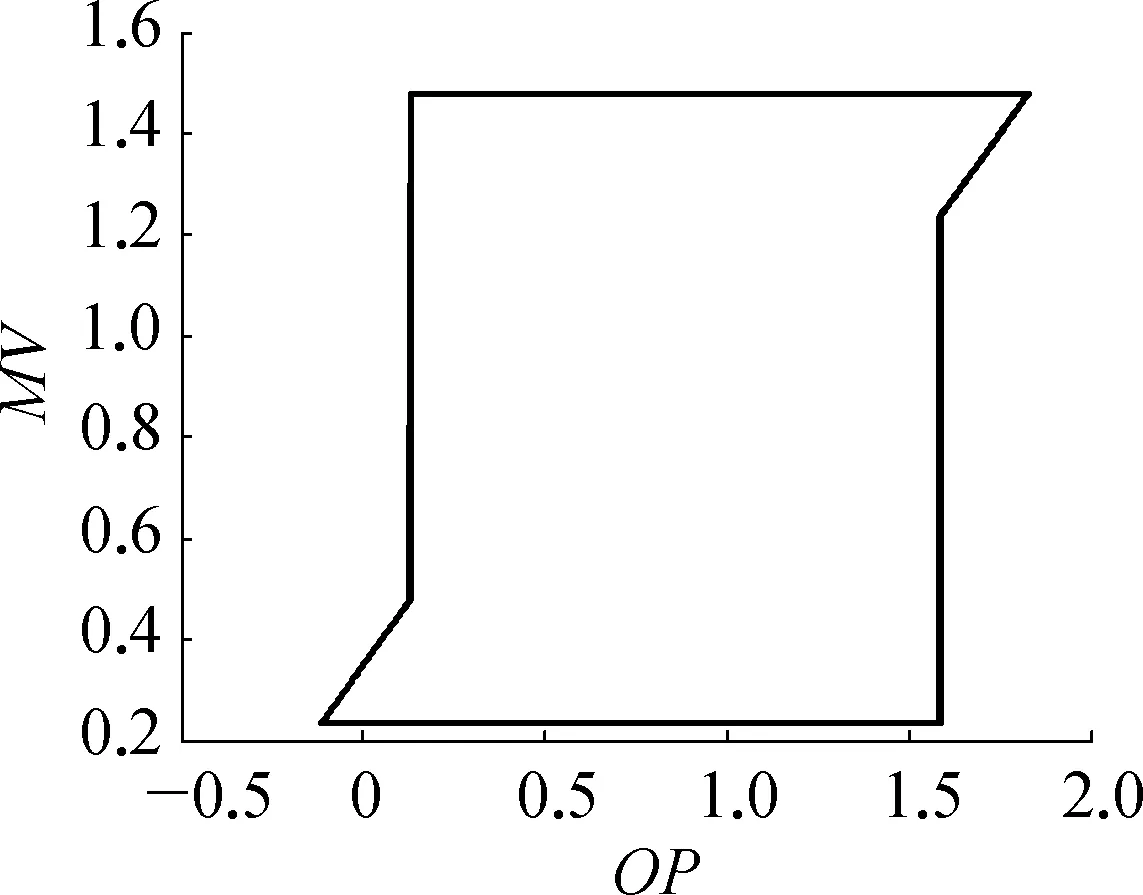
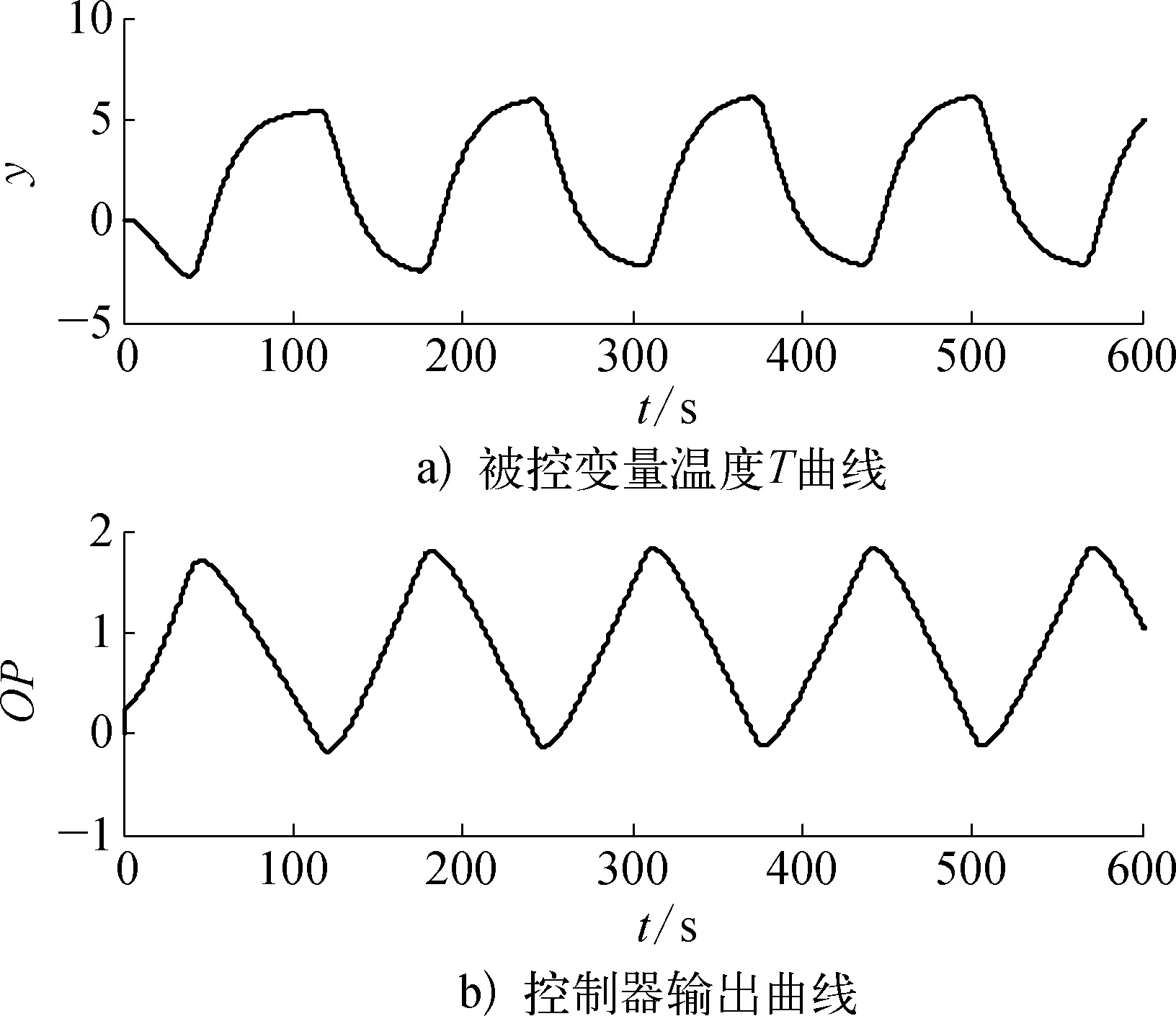
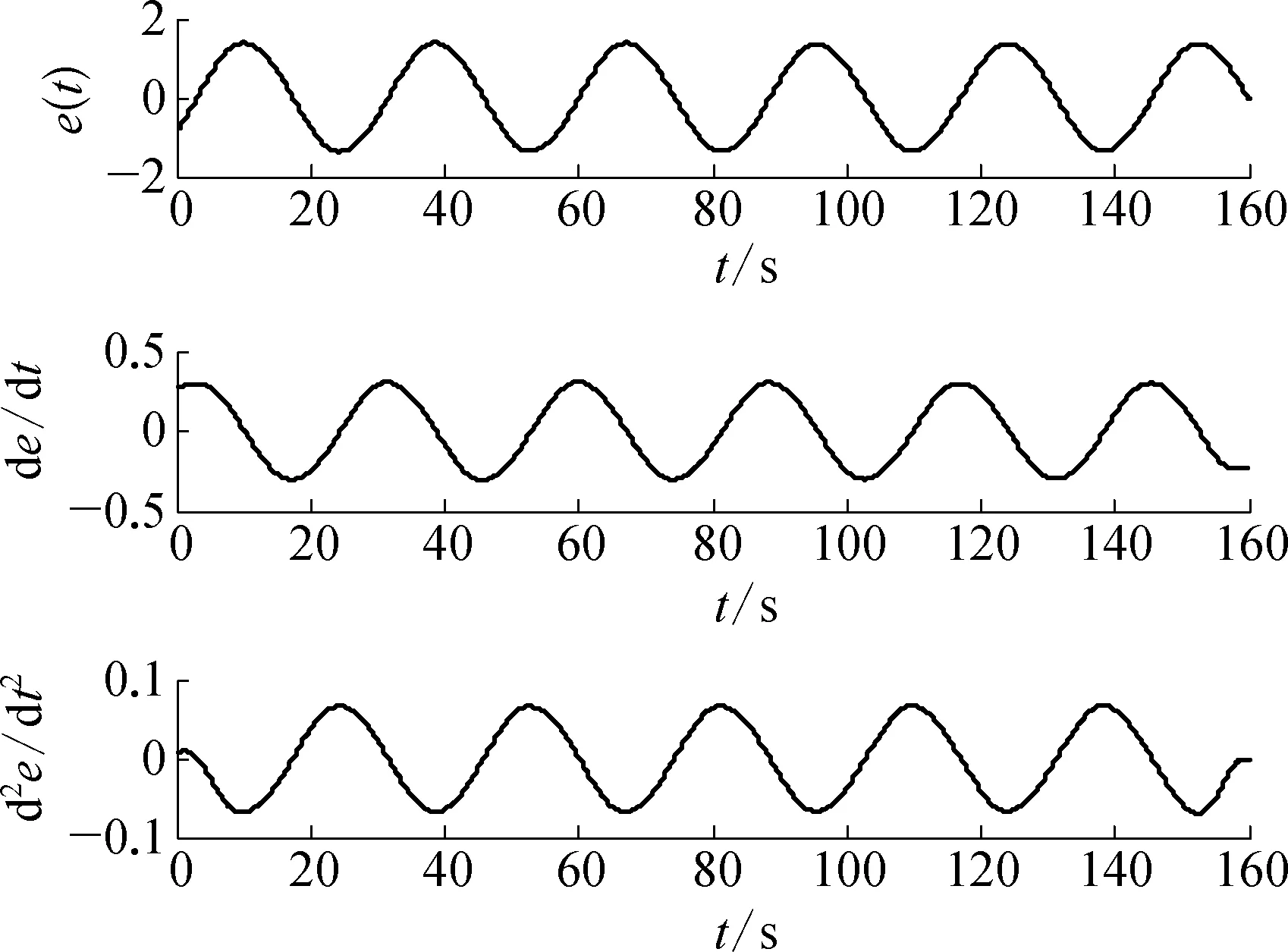
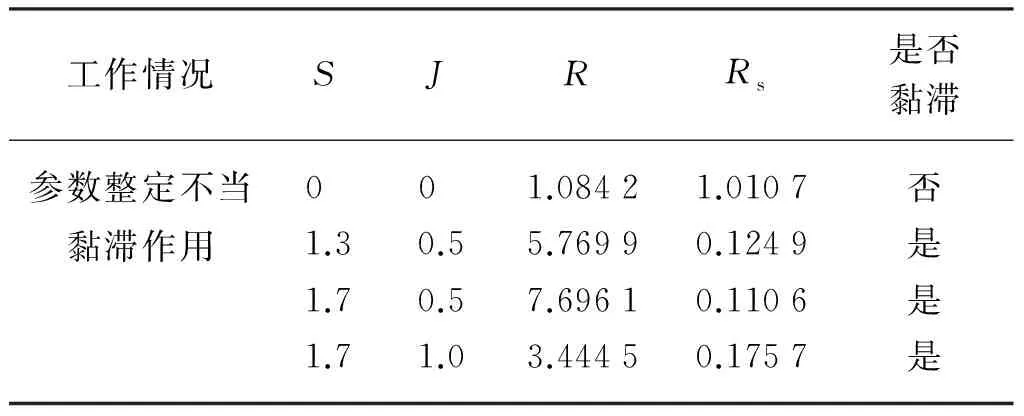
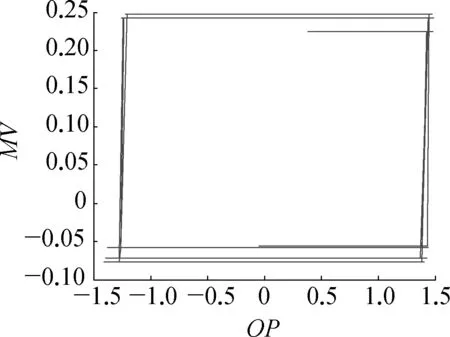
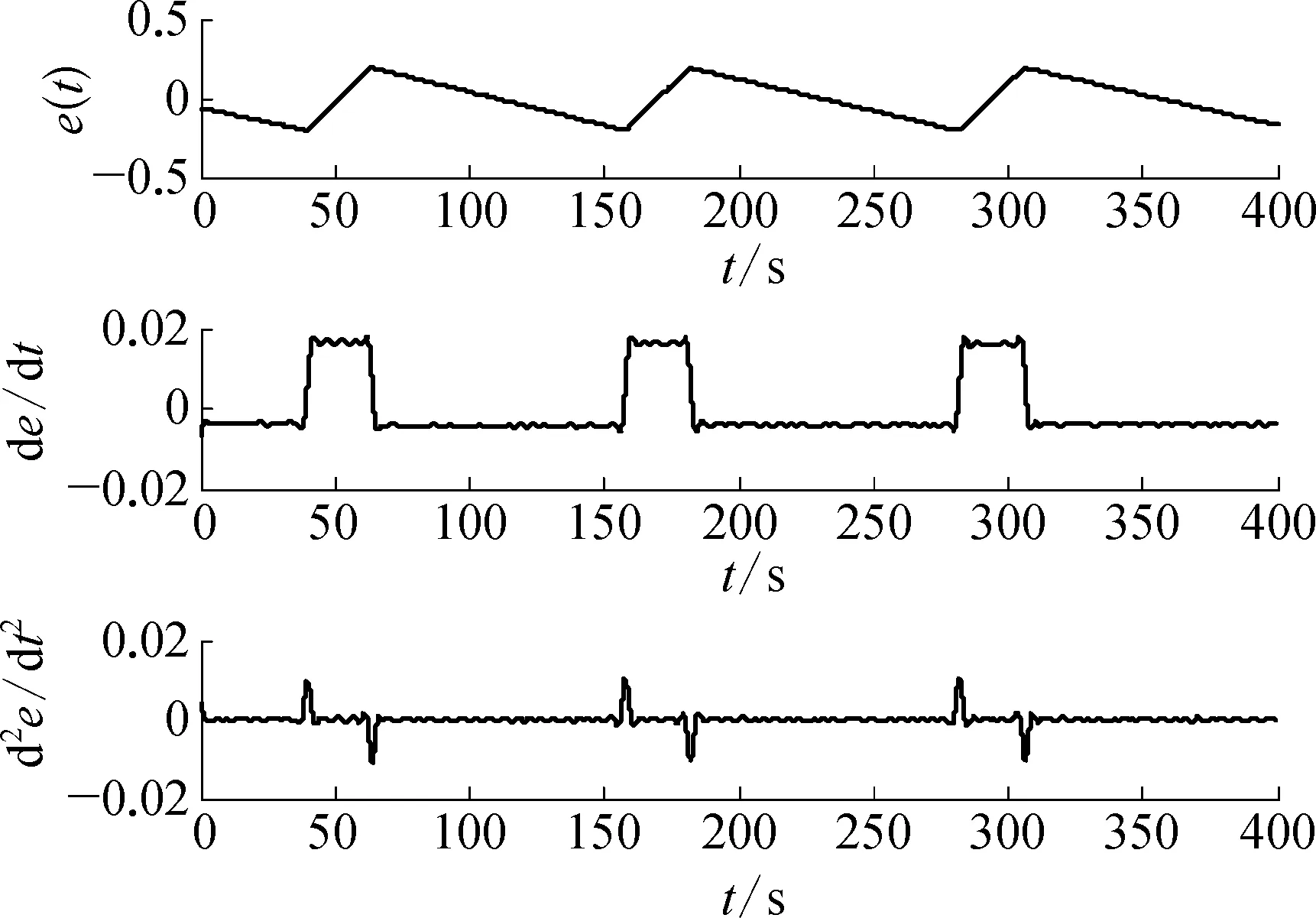
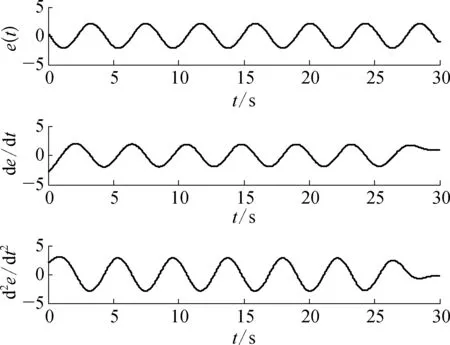
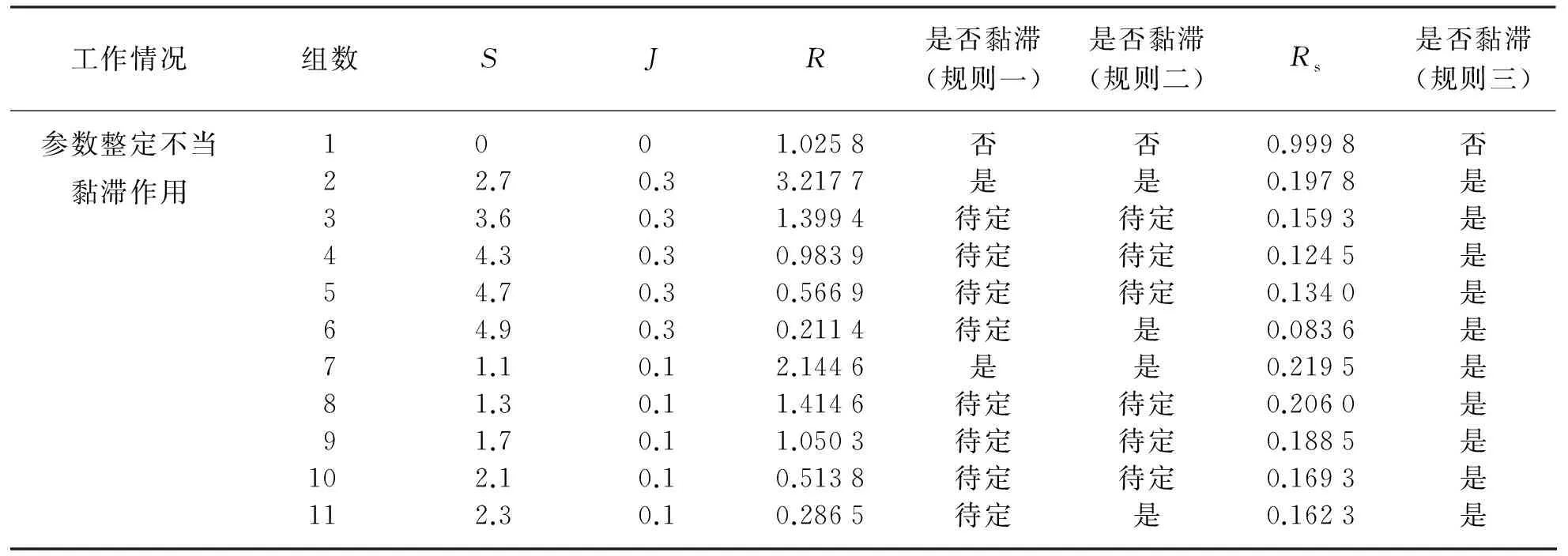
由于调节阀黏滞特性参数取值的不同，回路波形的不对称性包括A1>A2和A1

(3)

然而，由图3和图4可知，对于积分对象中的黏滞特性所导致的三角波信号和控制器参数整定不良导致的正弦信号，在采用式(3)的判断规则进行判断时均可能会得到R≈1的结果，即不能正确地检测到相应的黏滞特性和控制器参数整定不当。为解决上述问题，利用正弦信号与三角波信号二阶求导后所得信号的较大差异性进行检测判断，如图5所示。正弦信号经二次求导后成为相角发生偏移的正弦信号；而三角波信号经二次求导后成为正负交替的脉冲信号。基于此差异做进一步的检测。

由于周期信号求导后的幅值与原信号幅值成一定倍数关系，比值为角频率，因而提出基于二阶求导信号与原信号在1个振荡周期内面积比值的指标：

(4)

式中：As0——振荡回路偏差信号幅值归一化后所得信号在1个周期内与横轴围成的面积；As2——振荡回路偏差信号经过二阶求导后所得信号在1个周期内与横轴围成的面积。通过以上分析可知，如果Rs约等于0表明控制回路振荡信号近似为三角波信号，即调节阀存在黏滞作用；如果Rs约等于1表明回路振荡是由控制器参数整定不当所致，调节阀不存在黏滞作用。

因此对规则二进一步完善如下：

(5)

考虑到实际过程数据通常受到噪声干扰，且噪声信号的导数对指标影响较大，为易于工程应用，需要将各阶导数信号进行滤波且将上述规则描述如下，记为规则三：

(6)

图2 自衡对象存在黏滞特性时的偏差信号示意

图3 积分对象存在黏滞特性时的偏差信号示意

图4 控制器参数整定不当导致的偏差信号示意

图5 不同波形信号的二阶导数信号示意

其中检测阈值尚没有理论方法确定，往往只能通过反复试验的方式确定。由上面分析可以知道，改进的面积比值法可以适用于自衡对象和积分对象，克服了文献[13]的使用范围的局限性。下面的仿真实验验证了该方法的有效性。

3 仿真实验

3.1 自衡对象仿真研究

以某典型工业加热炉为仿真对象，其结构如图6所示，假设进料F恒定，通过调整燃料U来保证出口温度T恒定，建立模型如下：

采用PID控制器对加热炉回路进行控制，将进料值设置为F=1，设定值r=2，且控制回路运行良好时PID控制器参数为KP=0.11,KI=

0.008 5,KD=0，设置信噪比为70的高斯白噪声，分别在存在黏滞特性以及控制器参数整定不当的情形下进行仿真研究。

图6 典型工业加热炉结构示意

1) 调节阀存在黏滞特性时的情况。设置不同的调节阀黏滞参数使得回路发生振荡，当S=0.4,J=0.5时，图7为调节阀存在黏滞特性时的特性曲线，图8a)为被控变量温度T的曲线图，图8b)为控制器输出曲线图，图9为滤波后偏差的各阶导数数据，计算2个指标R和Rs进而判断引起回路振荡的原因，不同仿真参数下的指标结果见表1所列。

图7 自衡对象黏滞特性存在时阀门特性曲线示意

图8 自衡对象黏滞特性存在时回路数据示意

图9 自衡对象黏滞特性存在时 偏差各阶导数的数据示意

2) 控制器参数整定不当时的情况。将控制器参数设置为KP=0.817 5,KI=0.008 5,KD=0，此时回路发生振荡，图10为回路在控制器参数整定不当时调节阀的特性曲线，图11a)为被控变量温度T的曲线图，图11b)为控制器输出曲线图，图12为滤波后偏差的各阶导数数据，计算2个指标R和Rs进而判断引起回路振荡的原因，所得指标结果见表1所列。

图10 自衡对象控制器参数整定不当时 阀门特性曲线示意

图11 自衡对象控制器参数整定不当时 回路数据示意

图12 自衡对象控制器参数整定不当时 偏差各阶导数数据示意

工作情况SJRRs是否黏滞参数整定不当0 0 1.08421.0107否黏滞作用1.30.55.76990.1249是1.70.57.69610.1106是1.71.03.44450.1757是

通过表1得到的仿真结果，可以判断出第1组数据所对应的回路振荡是由控制器参数整定不当导致，而后3组数据所对应的回路振荡是由阀门黏滞特性引起，结论与振荡源的设置一致。

3.2 一阶积分对象仿真研究

考虑单回路控制，控制对象采用文献[20]中的一阶积分仿真对象，其传递函数为

采用PID控制器对回路进行控制，设定值r=2，且控制回路运行良好时PID控制器参数为KP=7,KI=0,KD=0，设置信噪比为50的高斯白噪声，分别在存在黏滞特性以及控制器参数整定不当情形下进行仿真研究。

1) 调节阀存在黏滞特性时的情况。设置不同的调节阀黏滞参数使得回路发生振荡，当S=2.3,J=1时，图13为调节阀存在黏滞特性时的特性曲线，图14a)为被控变量温度T曲线，图14b)为控制器输出曲线回路数据，图15为滤波后偏差的各阶导数数据，计算2个指标R和Rs进而判断引起回路振荡的原因，不同仿真参数下的指标结果见表2所列。

2) 控制器参数整定不当时的情况。将控制器参数设置为KP=22.44,KI=0,KD=0，此时，回路发生振荡，图16为回路在控制器参数整定不当时调节阀的特性曲线，图17a)为被控变量温度T曲线，图17b)为控制器输出曲线回路数据，图18为滤波后偏差的各阶导数数据，计算2个指标R和Rs进而判断引起回路振荡的原因，所得指标结果见表2所列。

图13 积分对象黏滞特性存在时阀门特性曲线示意

图14 积分对象黏滞特性存在时回路数据示意

图15 积分对象黏滞特性存在时偏差 各阶导数数据示意

图16 积分对象控制器参数整定不当时 阀门特性曲线示意

图17 积分对象控制器参数整定 不当时回路数据示意

图18 积分对象控制器参数不当时 偏差各阶导数数据示意

工作情况组数SJR是否黏滞(规则一)是否黏滞(规则二)Rs是否黏滞(规则三)参数整定不当10 0 1.0258否否0.9998否黏滞作用22.70.33.2177是是0.1978是33.60.31.3994待定待定0.1593是44.30.30.9839待定待定0.1245是54.70.30.5669待定待定0.1340是64.90.30.2114待定是0.0836是71.10.12.1446是是0.2195是81.30.11.4146待定待定0.2060是91.70.11.0503待定待定0.1885是102.10.10.5138待定待定0.1693是112.30.10.2865待定是0.1623是

通过表2得到的仿真结果，可以判断出第1组数据所对应的回路振荡是由控制器参数整定不当导致，后面10组数据是设置阀门黏滞特性引起的回路振荡，然而如果利用规则一进行判断，只有第1，2，7组能够给出准确的结论，其他情况下均待定；如果通过规则二进行判断，第1，2，6，7，11组能够给出准确的结论，相比规则一准确率增大；如果通过规则三进行判断，数据均能给出正确结论。结合指标Rs可以确切地判断振荡是由阀门黏滞特性引起，即该指标可检测积分对象，弥补了峰值前后面积比值法的不足。

4 结束语

针对面积峰值法应用范围的局限性，文中利用自衡对象和积分对象回路输出信号二阶导数的较大差异性，提出了一种改进的形状分析方法，能够高效且全面地进行黏滞特性检测，解决了许多检测方法仅适用于某一种对象的问题，但该方法计算过程中峰值的检测易受噪声影响，此时需要采用滤波方法提高准确性。仿真结果表明： 该方法可以准确可靠地对黏滞特性进行检测。

[1] Hägglund T. A Control-Loop Performance Monitor[J]. Control Engineering Practice, 1995, 3(11)： 1543-1551.

[2] Ender D B. Process Control Performance： Not as Good as You Think[J]. Control Engineering, 1993, 40(10)： 180-190.

[3] Årström K J. Assessment of Achievable Performance of Simple Feedback Loops[J]. International Journal of Adaptive Control Processing, 1991, 5(01)： 3-19.

[4] Taha O, Dumont G A, Davies M S. Detection and Diagnosis of Oscillations in Control Loops[C]//Decision and Control Proceedings of the 35th IEEE Conference： IEEE, 1996(03)： 2432-2437.

[5] Capaci R D, Scali C. Review on Valve Stiction. Part I： From Modeling to Smart Diagnosis[J]. Processes, 2015, 3(02)： 422-451.

[6] 张波.控制回路振荡、阀黏滞综合诊断平台的实现及工业应用研究[D].南京： 东南大学，2014.

[7] Choudhury M A A S, Shah S L, Thornhill N F, et al. Automatic Detection and Quantification of Stiction in Control Valves[J]. Control Engineering Practice, 2006, 14(12)： 1395-1412.

[8] Farenzena M, Trierweiler J O. Valve Stiction Estimation Using Global Optimisation[J]. Control Engineering Practice, 2012, 20(04)： 379-385.

[9] Capaci R B D, Scali C. Valve Stiction Quantification： a Robust Methodology to Face Most Common Causes of Loop Perturbations[C]//International Conference on Chemical and Process Engineering. Italy： Italian Association of Chemical Engineering, 2013： 1201-1206.

[10] Romano R A, Garcia C. Valve Friction Quantification and Nonlinear Process Model Identification[J]. IFAC Proceedings Volumes, 2010, 43(05)： 115-120.

[11] Kano M, Maruta H, Kugemoto H, et al. Practical Model and Detection Algorithm for Valve Stiction[C]//IFAC Symposium on Dynamics and Control of Process Systems. Holland： Elsevier, 2004： 5-7.

[12] Maruta H, Kano M, Kugemoto H, et al. Modeling and Detection of Stiction in Pneumatic Control Valve[J]. Transactions-society of Instrument and Control Engineers, 2004(40)： 825-833.

[13] Singhal A, Salsbury T I. A Simple Method for Detecting Valve Stiction in Oscillating Control Loops[J]. Journal of Process Control, 2005, 15(04)： 371-382.

[14] He Q P, Jin W, Pottmann M, et al. A Curve Fitting Method for Detecting Valve Stiction in Oscillating Control Loops[J]. Industrial & Engineering Chemistry Research, 2007, 46(13)： 4549-4560.

[15] Kalaivani S, Aravind T, Yuvaraj D. A Single Curve Piecewise Fitting Method for Detecting Valve Stiction and Quantification in Oscillating Control Loops[C]//Proceedings of the Second International Conference on Soft Computing for Problem Solving. Springer India, 2014： 13-24.

[16] Choudhury M A A S, Shah S L, Thornhill N F. Diagnosis of Poor Control-Loop Performance Using Higher-Order Statistics[J]. Automatica, 2004, 40(10)： 1719-1728.

[17] Thornhill N F. Finding the Source of Nonlinearity in a Process With Plant-Wide Oscillation[J]. IEEE Transactions on Control Systems Technology, 2005, 13(03)： 434-443.

[18] Horch A. A Simple Method for Detection of Stiction in Control Valves[J]. Control Engineering Practice, 1999, 7(10)： 1221-1231.

[19] Daneshwar M A, Noh N M. Detection of Stiction in Flow Control Loops Based on Fuzzy Clustering[J]. Control Engineering Practice, 2015(39)： 23-34.

[20] Kano M, Maruta H, Kugemoto H, et al. Practical Model and Detection Algorithm for Valve Stiction[C]//IFAC Symposium on Dynamics and Control of Process Systems. Holland： Elsevie, 2004： 5-7.

Study on Stiction Characteristics Detection Methods With an Improved Shaped Analysis

Kong Jie, Tian Xuemin, Shang Linyuan

(College of Information and Control Engineering, China University of Petroleum(East China), Qingdao, 266580, China)

Valve stiction is one of the main causes for control loop oscillation in industrial processes. Most of the existing control valve stiction detection methods are based on specific assumptions. It is only applicable for a specific scope. Aiming at the limitation that area peak method is only applicable to self-regulating object, an improved shaped analysis method is presented. Based on shape difference of loop output for self-regulating object and integral object, the larger difference for second derivative signal of vibration loop error and original signal are distinguished to conduct stiction characteristics detection. The method overcomes the limitation of area peak method only applicable to a particular range. The simulation experiment validates effectiveness and reliability of proposed method.Key words： stiction characteristics; oscillation diagnosis; control valve; nonlinear characteristics

国家自然科学基金(61273160，61403418)；山东省自然自然科学基金(ZR2014FL016，ZR2016FQ21)；中央高校基本科研业务费专项资金资助(13CX05021A，15CX06063A)。

孔杰(1990—)，女，黑龙江人，在读硕士研究生，主要研究方向为控制回路的振荡检测及诊断方法。

TP273

A

1007-7324(2017)03-0024-07

稿件收到日期： 2017-01-11，修改稿收到日期： 2017-03-06。