地下管线探测中全站仪偏心测量的方法及其精度分析
2017-07-05马道鸣


摘 要: 在地下管线探测的工程管线点坐标采集工作中,经常要对路灯、消防栓等柱状管线设施进行坐标采集,在采集此类管线点坐标时,由于棱镜无法直接置于点位上,需要进行偏心测量,进而取得设施中心点坐标,为了理清偏心测量对坐标精度造成的影响,并且为以后工作提供作业依据,笔者对偏心测量进行了一系列试验,得出了一些对测量工作有益的结论。
关键词: 偏心测量; 精度分析;地下管线探测
绪言
在地下管线探测工程中,需要对管线点坐标进行采集,目前主要依靠全站仪来进行采集,全站仪集测距、测角及微处理于一身,可直接进行三维坐标的测量。在全站仪采集坐标的过程中,经常会遇到柱状管线特征点或管线点被路灯、树木、车辆等障碍物遮挡的情况,这样就会用到偏心测量。本文介绍了全站仪在偏心测量中的观测原理及观测方法,并分析揭示了影响观测精度的主要因素和误差来源,同时为了理清偏心测量对点位采集精度造成的影响,并为在以后工作中提供作业依据,笔者也对单距偏心测量进行了一系列的试验,得到了一些对测量工作有益的结论。
1. 偏心测量的方法和原理
所谓全站仪偏心测量就是棱镜无法到达的点位,可通过观测与其相邻的可视点位后,通过相对关系,如角度和距离推算出这些视线无法到达的点位坐标,根据给定条件的不同,目前全站仪偏心测量有角度偏心测量、单距偏心测量、圆柱偏心测量和双距偏心测量4种方法。
1.1 角度偏心测量
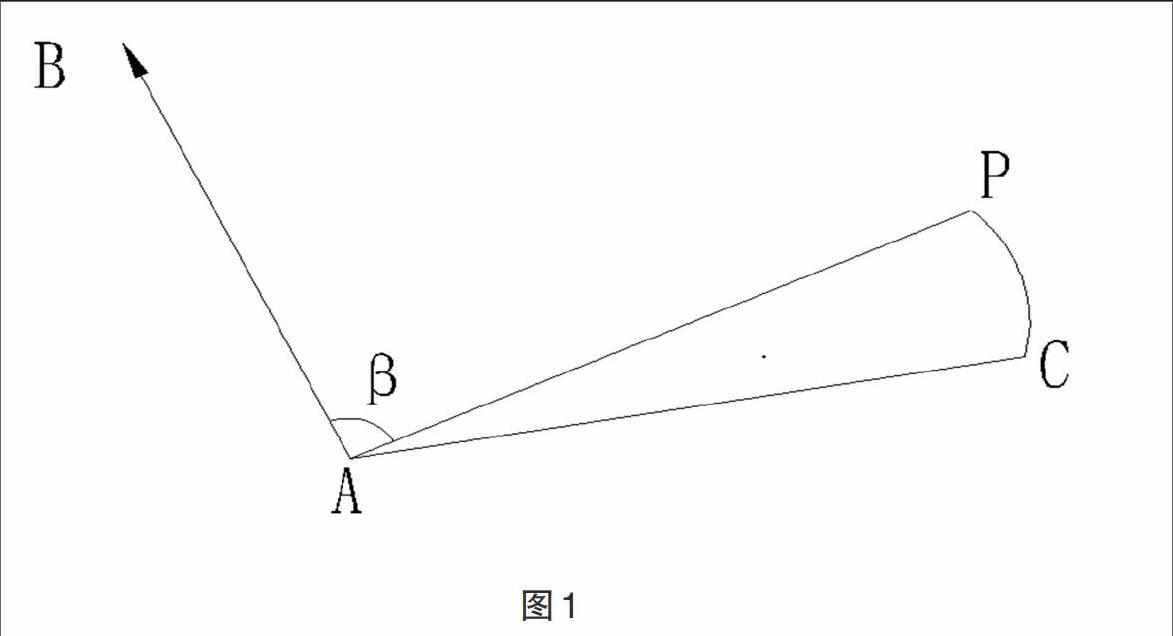
全站仪安置在某一已知点A,并照准另一已知点B进行定向;然后将偏心点C设置在待测点P的左侧(或右侧),并使其到测站点A的距离与待测点P到测站点的距离相当;接着对偏心点进行测量;最后再照准待测点方向,仪器就会自动计算并显示出待测点的坐标。其计算公式如下:
式中,和分别为测站点到偏心点(棱镜)的斜距和竖直角;,为已知点的坐标;为已知边的坐标方位角;为未知边与已知边的水平夹角;当未知边在已知边的右侧时,上式取“”。角度偏心测量适合待测点与测站点通视但其上无法安置反射棱镜的情况。
如图1所示:
在管线测量中角度偏心一般用在施测路灯杆,通信上杆等镜头无法立在点位中心的情况下。
1.2 单距偏心测量
如图2所示,待测点与测站点不通视。欲测定点,将全站仪安置在已知点,并照准另一已知点进行定向;将反射棱镜设置在待测点的附近一适当位置。然后输入待测点与偏心点间的距离和与的夹角,并对偏心点进行观测,仪器就会自动计算出待测点的坐标,或测站点至待测点的距离和方位角。计算公式如下:
式中,,为偏心点的坐标;为边与已知边的夹角;当和为右角时,上式取“”和“”。单据偏心测量适合于待测点与测站点不通视的情况。
在管线测量中单距偏心测量一般用在目标管线点被障碍物遮挡不通视,但是遮挡又不太严重偏移镜头离点位很近的距离就可以看见的情况下。
1.3 圆柱偏心测量
圆柱偏心测量是单距偏心测量的一个特殊情况,即待测点为某一圆柱形物体的圆心,如图3所示。观测时,全站仪安置在某一已知点,并照准另一已知点进行定向;然后,将反射棱镜设置在圆柱体的一侧点,且使与圆柱体相切;当输入圆柱体的半径,并对偏心点进行观测后,仪器就会自动计算并显示出待测点的坐标(,)或测站点至待测点的距离和方位角。其计算公式与单距偏心测量相同,只不过用和90°代替和。
由于圆柱的半径不一,又难以量取,在管线测量中圆柱偏心测量一般用角度偏心测量代替。
1.4 双距偏心测量
双距偏心测量,即棱镜无法到达的目标点,与两个棱镜杆构成3点一线的情况下,通过观测1号棱镜和2号棱镜后,再量取2号棱镜到目标点的距离,全站仪可推算出目标点的坐标。或者通过观测1号棱镜和2号棱镜后,水平转动望远镜瞄准目标点的方向,基于偏移的角度亦可推算出目标点的坐标,如图4所示,将全站仪安置在某一已知点,并照准另一已知点进行定向;然后将两点式觇牌对准待测点,分别测量和并输入点到待测点的距离,仪器便可计算并显示出待测点的坐标(,)或测站点至待测点的距离和方位角。
具体计算公式分别为
点的坐标
式中,和分别为边和边与已知边的水平夹角;当未知边和边在已知边的右侧时,上式取“”和“”;为两觇牌的间距。其他符号与前面公式相同。
由于双距偏心测量需要利用专制的两点式觇牌,携带不便在管线测量中很少用到。
2. 精度分析
从前面的介绍可知,全站仪偏心测量可有多种方式,其相应的计算公式亦有所不同;但他们都有一个共同的基本公式。为此,我们先分析这个公式的误差情况。
对公式取全微分并转换为中误差(不顾及已知数据误差),可得点的点位中误差为
式中,和分别为竖直角和水平角的测角中误差;为测距中误差。
现设=,又因≤1,所以上式可写成
若取mm,时,但=100m,mm;
当S=1000m,mm。
由此可見,仅顾及测角和测距误差,全站仪极坐标法测定一点的平面精度完全可以满足一般测量工作的要求。但在此基础上形成的全站仪偏心测量,其精度还需要进一步分析。如角度偏心测量,公式中的和分别为测站点到偏心点(棱镜)的斜距和竖直角,并非是测站点到待测点的斜距和竖直角;代替的前提是测站点到待测点和到偏心点的距离相当,即;若不等,将直接影响待测点的点位中误差,影响值即为偏差值。因此,角度偏心测量的主要误差来源于偏心点位置的选取。同样,对于单距偏心测量,其主要误差来源于偏心距和偏心角的测定误差;对于圆柱偏心测量,其主要误差来源于半径的测定误差和偏心点位置的选取(即与是否垂直)。至于利用专制的两点式觇牌进行的双距偏心测量,由于和可以精确量取,其测定误差主要来源于全站仪测定和的误差;但应注意:由于值较小(一般为0.5m),为了保证必要的精度,最大测程不要超过100m。
3.对单距偏心测量的进一步精度分析
前面提到,在管線测量中对管线点的采集主要用到了角度偏心测量与单距偏心测量,由于角度偏心测量一般可以看见目标点的中心,只要把握好偏心位置,尽量让偏心点与待测点距测站的距离相当,精度相对较好控制。但是单距偏心测量因为看不到目标点,不同的偏距和视距在实际操作中对精度的影响较大,为了研究偏心距离与视距对偏心点精度的影响,笔者以拓普康系列全站仪做了如图5所示实验:在距离设站点一条直线上设定5m、10m、25m、50m、100m5个点位,每个点位按照不同的偏距进行距离偏心观测,由于此类仪器的距离偏心只需输入左右偏距和前后偏距,角默认为90°,为了贴近日常生产情况,所以在设置偏心点时,采用在仪器与原点基线垂线上选点的方法。通过偏心测量所测坐标与原点位坐标进行比较计算出两点距离的较差,并经过多次测量取得误差平均值,具体结果见下表。
通过上表可以看出,随着测量距离的缩短和偏心距离的扩大,偏心的误差会逐步扩大,在管线探测工程的国家规范中,地下管线点的测量精度:平面位置测量中误差不得大于±5cm(相对于临近控制点),因此在通常情况下视距大于10米偏心距离小于50cm时,可以满足管线点的测量精度。
但在管线探测实际工作中,由于地形的复杂,以及偏心点的选择前后位移可能较大,这些都会影响测量精度,因此在实际工作中应尽量少用或不用偏心测量,以提高测量精度,如一定需要偏心测量时,应该尽量准确的选取偏心点位量,并且控制好视距与偏距。
参考文献:
[1] 焦文海, 魏子卿. 1985国家高程基准相对于大地水准面的垂直偏差[C]// 中国科协2002年学术年会测绘. 2002:196-200.
[2] 顾旦生, 张莉. 我国大地坐标系发展目标[J]. 测绘通报, 2003(3):1-4.
[3] 陈俊勇. 关于中国采用地心3维坐标系统的探讨[J]. 测绘学报, 2003, 32(4):283-288.
[4] 郭宗河, 郑进风. 全站仪面积测量及其精度分析[J]. 测绘通报, 2002(3):30-31.
[5] 姚姝娟, 宝力杰, 沈文慧. 地下管线三维信息系统在城市规划中的现实意义[J]. 西部资源, 2015(2):176-178.
[6] 郝洋洲, 周长军. 城市地下管线横断面的设计与绘制[J]. 西部资源, 2013(1):162-164.
