高斯函数定权的改进KNN室内定位方法
2017-07-05毕京学汪云甲刘笑笑
毕京学,甄 杰,汪云甲,刘笑笑
(1. 中国矿业大学,江苏 徐州 221116; 2. 中国测绘科学研究院,北京 100830)
高斯函数定权的改进KNN室内定位方法
毕京学1,甄 杰2,汪云甲1,刘笑笑1
(1. 中国矿业大学,江苏 徐州 221116; 2. 中国测绘科学研究院,北京 100830)
室内某些区域无线访问接入点(AP)布设稀疏,以及信号指纹的时变特性等因素,均使得无线信号接收信号强度(RSSI)序列与射电地图(radio map)相应RSSI序列完全相同成为可能,计算得到信号空间的欧氏距离为0或非常小。利用欧氏距离定权的加权质心算法解算会出现错误,无法得到定位结果;取K个参考点坐标均值的KNN算法以1/K为权值,定位精度相对较低。本文提出了高斯函数定权的KNN定位算法,对K个最近邻欧氏距离进行了标准化处理,利用高斯函数分配权值,得到加权坐标值。与KNN和WKNN算法的定位结果相比,该方法提高了鲁棒性和定位精度。
信号接收强度;欧氏距离;高斯函数;定权;K最近邻;室内定位
室内定位技术是基于位置服务的研究热点,许多研究机构、公司和大学利用红外线[1]、超声波[2]、射频识别[3](radio frequency identification,RFID)、ZigBee[4]、无线局域网[5](wireless local area network,WLAN)、蓝牙[6]、微机电系统(micro electro mechanical systems,MEMS)传感器[7]、超宽带[8](ultra-wideband,UWB)、地磁[9]、可见光通信[10]、计算机视觉[11]、伪卫星[12](Pseudolites)等技术开展了大量研究工作,开发了相应的室内定位系统,并结合文献[13]总结了不同定位技术的定位精度,如图1所示。
自微软研究院推出基于WiFi技术的RADAR[14]室内定位系统以来,基于WiFi接收信号强度室内定位技术由于不需要添加额外设备,容易开展试验,且方便推广,在理论和商业应用方面取得了较大成果。其中,K最近邻(K-nearest neighbor,KNN)算法由于算法简单、易于实现被广泛研究。在KNN定位算法的基础上,有些研究人员对KNN算法在权值分配和自适应K值作了改进。Dudani[15]首先将加权投票机制引入KNN中,称为距离加权KNN。Lionel[16]等在KNN算法的基础上提出了K加权近邻法(weighted K nearest neighbors,WKNN),以待测点与参考点之间在信号空间的欧氏距离分配权重进行加权处理得到加权均值坐标,提高了定位精度。但是该算法中的K值固定不变,无法兼顾所有测试点的定位精度,Beomju[17]测试发现在KNN和WKNN算法中以K值取5时的定位结果最优;同时,针对固定K值会引入实际距离偏离待定点较远的参考点问题,提出了动态加权EWKNN算法,该算法设定了初始阈值,动态选择K值,提高了定位精度[18]。陈国良[19]将聚类分析方法应用到指纹定位,有效缩短了计算时间;王磊[20]利用平均加权KNN算法与地图约束相结合,提升了30%的定位精度;牛建伟[21]提出了属性加权K近邻算法,将无球访问接点(access point,AP)之间的相关性用于权值分配上,在AP数量较多的情况下有较好的定位效果。但是忽略了欧氏距离很小或为0的情况,而且指纹库几何位置边缘或参考点稀疏区域权值分配不合理。本文提出基于高斯函数定权的KNN室内定位方法,对K个欧氏距离进行标准化处理,利用高斯函数分配权值,以提高定位精度。

图1 已有室内定位技术定位精度示意图
1 KNN室内定位
1.1 基于无线接收信号强度(RSSI)指纹匹配定位原理
RSSI(received signal strength indicator,RSSI)指纹匹配定位分离线(offline phase)与在线(online phase)两个阶段,如图2所示。离线阶段主要是信息采集和样本训练,利用参考点的已知位置数据和接收到的接入点的RSSI信号特征值(RSSI、MAC地址、最值、均值、方差、方向、概率等)建立位置—指纹数据库,从而建立空间位置与RSSI序列的映射关系;在线定位过程则是利用接收到的目标点RSSI序列与位置指纹数据库进行匹配,运用某一定位算法,解算出待定点的位置信息。

图2 基于RSSI指纹匹配定位原理
1.2 KNN室内定位
Bahl[14]等首次将KNN法应用到基于RSSI的室内定位研究中,利用实测RSSI均值与位置指纹数据库进行搜索匹配运算,计算出参考点与待测目标在信号空间(signal space,SS)中的距离,选择K个最小信号空间距离对应的参考点坐标取均值作为当前待测目标的估计位置。
RSSI均值作为特征量,构建位置指纹数据库D=(Li,Fi),i=1,2,…,n,n为参考点个数。其中,Li为第i个参考点的坐标向量,Fi为第i个参考点的RSSI信号特征矩阵,mac为搜索到AP的硬件地址(medium access control,MAC),μ为RSSI均值,由于AP布设、建筑物结构的不同,不同参考点可搜索到的AP在名称与个数上不一致,因此Fi应是变维矩阵。
(1)
以欧氏距离作为参考点与待测目标点相似性的衡量,欧氏距离越小,两点越临近。假设待测点扫描到m个AP且与第i个参考点的位置指纹库中AP的MAC地址均一致,则欧氏距离计算公式为

(2)

(3)
2 高斯函数定权的KNN
提出的高斯函数定权KNN方法有以下几个步骤:计算欧氏距离、降噪处理、标准化处理、高斯函数定权、加权均值。
2.1 降噪处理
利用指纹匹配定位原理可得到信号空间的欧氏距离di(i=1,2,…,n),n为当前指纹库的参考点个数,如果指纹库是经过聚类处理的,则n为聚类指纹库中参考点的个数。由于移动终端扫描到的RSSI为随机信号,因此计算得到的欧氏距离是随机变量。假设欧氏距离服从正态分布,计算均值和中误差的公式分别为
(4)
以2倍中误差作为偶然误差的允许误差,剔除式(5)范围内的欧氏距离和参考点坐标,生成新的欧氏距离和参考点序列,并利用式(4)重新计算均值μd和中误差σd。
(5)
2.2Z-score标准化和高斯函数定权
利用式(6)对K个近邻欧氏距离进行Z-score标准化处理,其中j=1,2,…,K,则符合标准正态分布,利用高斯函数式(7)计算权值
(6)
(7)
2.3 加权均值
选取K个最近邻欧氏距离对应的参考点,利用式(8)计算得到加权坐标均值
(8)
高斯函数定权的KNN定位算法伪代码如下
(1) 计算扫描指纹到参考点的欧氏距离:
for i=1 to n
di=0
for j=1 to m
ifFingerPrinticontains mac

else

end
end
(2) 降噪处理(得到了n个欧氏距离序列):
for i=1 to n
从欧氏距离序列中删除di,删除对应参考点
end
对新的欧氏距离序列取均值和中误差,得到K个最近邻距离Dknn及对应坐标Pknn。
(3) 标准化及定权处理:
for i=1 to K
end
(4) 加权均值为
3 试验测试
3.1 试验描述
试验场设置在北京市东直门内北小街北京帝测科技有限公司,安装有14个2.4 Hz/5 Hz双频AP,可以实现公司办公区域内信号全覆盖,如图3所示,黑色五角星代表部署的AP。利用自主开发的指纹采集软件扫描并存储数据,如图4所示。由于含有办公桌椅,并不是严格按照2 m间隔取点。在离线采样阶段,以1 s的频率采集AP的RSSI,每次采集30 s,取其均值作为信号特征值存储到指纹数据库中,参考点共有150个。
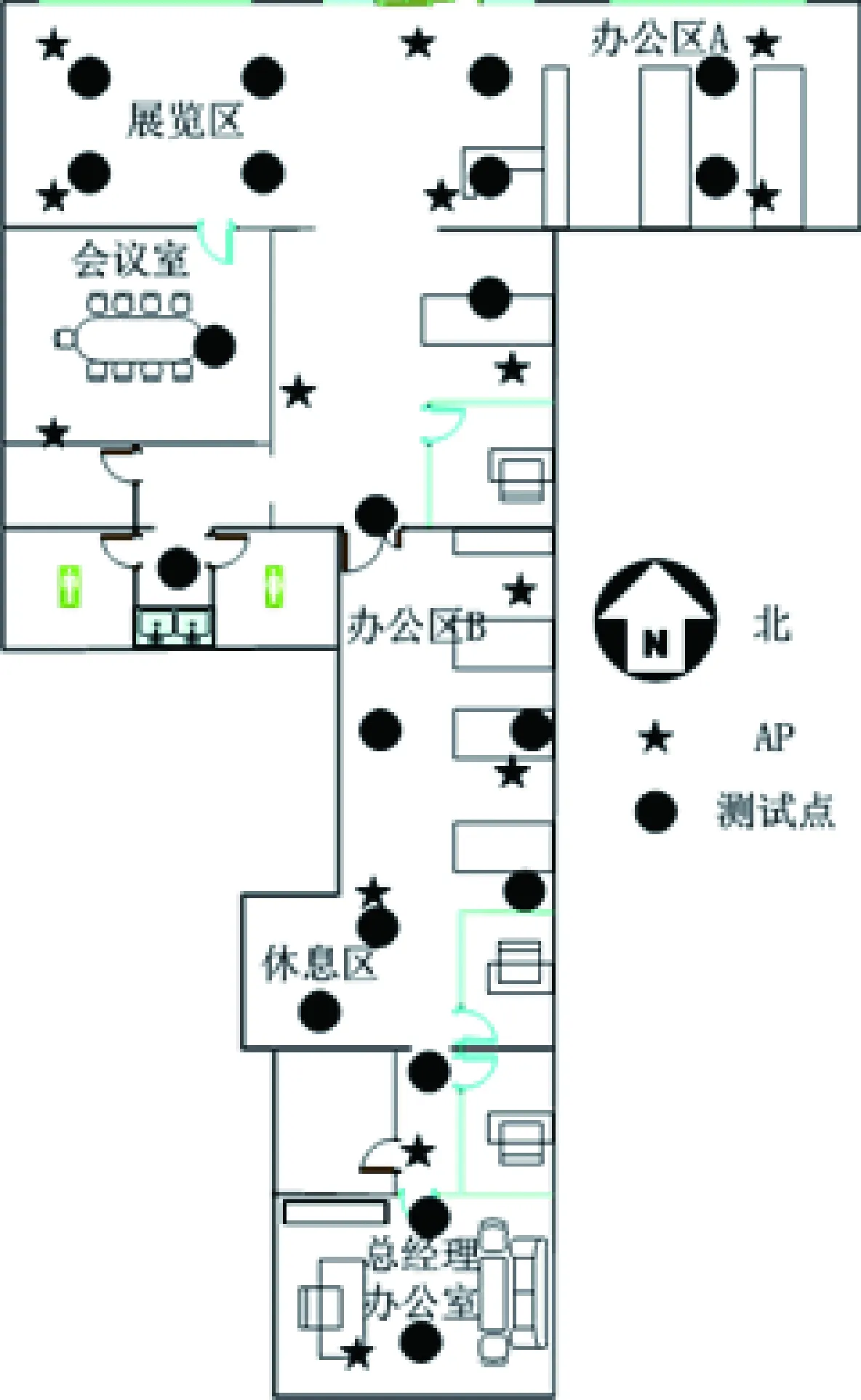
图3 试验区域

图4 指纹采集软件
3.2 试验结果与分析
在利用KNN指纹匹配法计算欧氏距离时,若指纹库中无扫描到AP,将RSSI值设定为-95 dBm[22]参与计算。如图5所示,在展览区、办公区A和B、会议室、休息区、总经理办公室等位置选取了20个测试点进行静态测试,与指纹采集时朝向一致。设定K为5,分别利用KNN、WKNN与GWKNN算法计算,比较定位结果并进行分析。

图5 定位误差累计概率分布
从图5中可以看出,GWKNN算法定位精度优于3 m的概率约为74%,而WKNN和KNN定位精度优于3 m分别为60%和40%;这是由于办公区域内布局复杂,含有桌椅等用品,同时,参考点分布不均匀,人员走动频繁,定位结果表现较差。
从表1可以看出,3种算法定位误差最大值均高于5.7 m,这是因为洗手间、会议室附近AP布设稀疏,采集参考点数目较少,计算过程中引入多余参考点增大了定位误差;从定位误差均值看来,GWKNN定位效果要比WKNN和KNN好。

表1 定位误差对比 m
由此可知,本文提出的GWKNN算法相对于WKNN和KNN算法,尽管算法复杂度提高了,但无论在定位稳定性还是在定位精度方面都有显著提高。
4 结 语
本文提出了高斯函数定权的加权KNN室内定位算法,该方法通过对欧氏距离进行降噪处理剔除允许误差(2倍中误差)外的欧氏距离和参考点,标准化处理后,利用高斯函数对K个最近邻欧氏距离分配权重,加权取均值。与KNN和WKNN室内定位算法相比,避免了直接利用欧氏距离定权的计算错误,提高了定位精度。试验中K取值为5,指纹库几何位置边缘或参考点稀疏区域会引入定位误差,自适应K值室内定位方法还需进一步研究。
[1] WANT R, HOPPER A, FALCAO V, et al. The Active Badge Location System[J]. ACM Transactions on Information Systems, 1992, 10(1): 91-102.
[2] PRIYANTHA N B, CHAKRABORTY A, BALAKRISH-NAN H. The Cricket Location-support System[C]∥Proceedings of the 6th Annual International Conference on Mobile Computing and Networking. [S.l.]: ACM, 2000: 32-43.
[3] CHAWLA K, MCFARLAND C, ROBINS G, et al. Real-time RFID Localization Using RSS[C]∥2013 International Conference on Localization and GNSS (ICL-GNSS). [S.l.]: IEEE, 2013: 1-6.
[4] SUGANO M, KAWAZOE T, OHTA Y, et al. Indoor Localization System Using RSSI Measurement of Wireless Sensor Network Based on ZigBee Standard[C]∥International Multi-conference on Wireless Optical Communications. Banff: IASTED/ACTA Press,2000.
[5] MAZUELAS S, BAHILLO A, LORENZO R M, et al. Robust Indoor Positioning Provided by Real-time RSSI Values in Unmodified WLAN Networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(5): 821-831.
[6] FELDMANN S, KYAMAKYA K, ZAPATER A, et al. An Indoor Bluetooth-Based Positioning System: Concept, Implementation and Experimental Evaluation[C]∥Proceedings of the International Conference on Wireless Networks. Las Vegas: [s.n.], 2003: 109-113.
[7] GLANZER G, BERNOULLI T, WIESSFLECKER T, et al. Semi-autonomous Indoor Positioning Using MEMS-based Inertial Measurement Units and Building Information[C]∥6th Workshop on Positioning Navigation and Communication, WPNC 2009. Hannover: IEEE, 2009: 135-139.
[8] ALAVI B, PAHLAVAN K. Modeling of the TOA-based Distance Measurement Error Using UWB Indoor Radio Measurements[J]. IEEE Communications Letters, 2006, 10(4): 275-277.
[9] INDOORATLAS L. Ambient magnetic field-based indoor location technology: Bringing the compass to the next level[J]. IndoorAtlas Ltd, 2012.
[10] ZHOU Z, KAVEHRAD M, DENG P. Indoor Positioning Algorithm Using Light-emitting Diode Visible Light Communications[J]. Optical Engineering, 2012, 51(8): 5009.
[11] WERNER M, KESSEL M, MAROUANE C. Indoor Po-sitioning Using Smartphone Camera[C]∥International Conference on Indoor Positioning Indoor Navigation. [S.l.]: IEEE, 2011: 1-6.
[12] BARNES J, RIZOS C, WANG J, et al. Locata: A New Positioning Technology for High Precision Indoor and Outdoor Positioning[J]. Journal of Chemical Physics, 2003, 118(15): 6717-6719.
[13] LIU H, DARABI H, BANERJEE P, et al. Survey of Wireless Indoor Positioning Techniques and Systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(6): 1067-1080.
[14] BAHL P, PADMANABHAN V N. RADAR: An In-building RF-based User Location and Tracking System[C]∥ Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies. [S.l.]: IEEE, 2000: 775-784.
[15] DUDANI S A. The Distance-weighted K-Nearest-Neighbor Rule[J]. IEEE Transactions on Systems, Man and Cybernetics, 1976, 6(4): 325-327.
[16] NI L M, LIU Y, LAU Y C, et al. LANDMARC: Indoor Location Sensing Using Active RFID[J]. Wireless Networks, 2004, 10(6): 701-710.
[17] SHIN B, LEE J H, LEE T, et al. Enhanced Weighted K-nearest Neighbor Algorithm for Indoor Wi-Fi Positioning Systems[C]∥2012 8th International Conference on Computing Technology and Information Management (ICCM). [S.l.]: IEEE, 2012: 574-577.
[18] 王培重, 郑南山, 张言哲. 基于动态 K 值及 AP MAC 地址筛选的室内定位算法[J]. 计算机科学, 2016, 43(1): 163-165.
[19] 陈国良, 张言哲, 汪云甲, 等. WiFi-PDR 室内组合定位的无迹卡尔曼滤波算法[J]. 测绘学报, 2015, 44(12): 1314-1321.
[20] 王磊, 周慧, 蒋国平, 等. 基于 WiFi 的自适应匹配预处理 WKNN 算法[J]. 信号处理, 2015, 31(9):1067-1074.
[21] 牛建伟,刘洋,卢邦辉,等.一种基于Wi-Fi信号指纹的楼宇内定位算法[J].计算机研究与发展,2013,50(3):568-577.
[22] 杨凯, 郭英, 毕京学. 基于安卓平台的室内实时定位[J]. 测绘科学, 2015, 40(6): 125-128.
引文格式: 朱添翼,范强,杜漫飞.一种遥感图像建筑物直线特征提取算法[J].测绘通报,2017(6):36-39.DOI:10.13474/j.cnki.11-2246.2017.0185.
The Method of Enhanced Gaussian Function Weighted KNN Indoor Positioning
BI Jingxue1,ZHEN Jie2,WANG Yunjia1,LIU Xiaoxiao1
(1. China University of Mining and Technology, Xuzhou 221116, China; 2. Chinese Academy of Surveying and Mapping, Beijing 100830, China)
Because of less deployed APs in some indoor areas and signal fingerprint time-varying characteristics, it is possible for the currently scanning RSSI vector to be similar to corresponding RSSI sequence which is stored with location in radio map. In these cases, the calculated Euclidean distance is usually 0 or very small. Error will occur when the Euclidean distance is used for weight value in weighted centroid algorithm, and no result will be obtained. And KNN algorithm, which supposes the value 1/Kas weight, will get the average of coordinates ofKreference points along with relative low positioning accuracy. Therefore, Gaussian weighted KNN (GWKNN) localization algorithm is proposed: standardization processes forKnearest Euclidean distances were made, then corresponding weights were distributed by Gaussian function, at last, the weighted positioning result is obtained. Compared with the positioning results of KNN and WKNN algorithm, this positioning method can get higher robustness and positioning accuracy.
RSSI;Euclidean distance;Gaussian function;assign weights;KNN; indoor positioning
毕京学,甄杰,汪云甲,等.高斯函数定权的改进KNN室内定位方法[J].测绘通报,2017(6):9-12.
10.13474/j.cnki.11-2246.2017.0179.
2016-09-20 基金项目: 国家重点研发计划(2016YFB0502102);国家863计划(2013AA12A201);江苏省普通高校学术学位研究生创新计划(KYLX16_0544)
毕京学(1991—),男,博士生,研究方向为室内外无缝定位。E-mail:bjx1050@163.com
汪云甲。E-mail:wyj4139@cumt.edu.cn
P228
A
0494-0911(2017)06-0009-04
