基于交通运输问题的模糊多目标规划模型

刘 睿，李 华，李钰蒙

(西安航空学院 理学院，陕西 西安 710077)

基于交通运输问题的模糊多目标规划模型

刘 睿，李 华，李钰蒙

(西安航空学院 理学院，陕西 西安 710077)

从销售商的角度出发，建立了生产-销售的模糊多目标交通运输模型。该模型以寻求最少交通时间，最低运输成本为目标。同时要求销售地的进货量尽可能的满足市场需求量且不超过仓库存储能力，销售地的总进货量尽可能不大于生产地的预计供货能力且不超过生产地的最大供货能力，商品购买成本与运输费用之和尽可能不大于预算成本。并引进不确定分布函数与隶属度函数将该模型转换为确定型多目标规划模型。其次，借助maxmin法将该确定型模糊多目标规划模型转换为单目标线性规划模型进行求解。最后，借助于台湾某公司的实例来验证了所提出模型与求解方法的有效性和可行性。

模糊多目标规划；不确定分布函数；隶属度函数；maxmin法

0 引言

面对当前市场经济下的激烈竞争，各个企业为了增强企业竞争力，提高企业利润，都在致力于降低商品的成本。而商品成本是由商品的生产成本与运输成本共同构成。降低商品的生产成本需要从采购原材料、提高生产质量、减少机械折旧率等方面入手，需要投入大量的人力物力。而在现有条件下降低运输成本，只需制定出产地与销地之间合理的运输方案，以降低运输成本、加快运输速度、保证有效运输量。该方法不失为一种更加切实可行的方案。故如何制定生产-销售的交通运输方案对大多数企业来说是急需解决的问题。

传统的运输问题一般指单目标运输问题，其目标是最少的运输成本，是一类特殊的线性规划问题，可以用表上作业法来求解[1]。但在实际的商品运输中，企业需要考虑的因素不仅仅是降低运输成本，同时还需要尽可能的缩短运输时间、提高运输安全及运输可靠性，而这些因素之间是相互矛盾对立的，无法归一为单目标运输规划问题。因此建立多目标运输规划问题就显得十分必要。

而在市场经济的大环境中，市场的需求量(销售量)及商品的可供应量虽然可以做出预估计，却极有可能因为一些不可抗因素或者市场供需关系的变化而变化。商品的运输成本、运输时间、运输可靠性等虽然也会有一个预计量，但其也会随着路况的变化而变化。综上所述，将生产-销售的交通运输方案建立为模糊多目标线性规划更符合实际情况。

Zimmermann首次使用maxmin法来求解模糊多目标线性规划问题[2]。但是，该方法求得的解并不是唯一有效的[3-5]，故很多研究者致力于寻找一种更加有效的求解方法。其中，Lai和Hwang[4]提出了参数最大最小法，Selim和Ozkarahan[6]改进了Werner法[7]。Torabi和Hassini结合了Lai和Hwang[4]的参数maxmin法与Selim和Ozkarahan[6]的改进Werner法，提出了新的单阶段模糊法来求解模糊多目标线性规划。Chana[8]提出了交通运输的明确值模型、区间值模型及模糊模型并讨论了其求解方法。Shih针对台湾提出了交通运输的模糊线性规划模型。Liu和Kao[9]借助于隶属度函数来求解交通运输模糊模型。Zadeh[10]将模糊交通问题转换为一对数学规划问题。Liang[11]提出了交互式模糊多目标线性规划来求解模糊多目标交通问题。

在求解模糊交通规划问题时，大多数研究者都借助于了隶属度函数[12]。介绍了很多种可用于求解模糊交通规划的隶属度函数。本文借助于不确定函数来求解模糊多目标规划问题。

1 模型建立

模型假设，现有m个生产地，依次记为Si，i=1，2，…，m，n个销售地，依次记为Dj，j=1，2，…，n。Qij，i=1，2，…，m，j=1，2，…，n表示从生产地Si到销售地Dj的运输量。pi，i=1，2，…，m表示从生产地Si生产的货物的单位出厂价格。cij，i=1，2，…，m，j=1，2，…，n表示从生产地Si到销售地Dj的单位运价。tij，i=1，2，…，n表示从生产地Si到销售地Dj的单位货物运输时间。如图1所示。

而在市场经济中，先购买再出售，故市场的需求量(销售量)是可以做出预估计的，并不是一成不变的。同时，生产地的预期供货量也可能因为劳动力缺乏或过剩、生产机器的维修、停水停电等不可抗因素而造成改变。商品的出厂价格与商品预算最高进价，也会因为市场供需变化而发生变化，商品的运输时间也会随着天气、道路、交通状况等的变化而不断变化。故对于销售地来说，商品成本与运输时间是在不断变化的。

综上所述，生产-销售的交通运输计划是致力于寻找最少交通时间及最低运输成本。与此同时，销售地的进货量还应该尽可能的满足市场需求量且不超过仓库存储能力，商品的购买量尽可能不大于生产地的预计供货能力且不超过生产地的最大供货能力，商品购买成本与运输费用之和尽可能不大于预算成本。由此可知，生产-销售的交通运输计划模型应为模糊多目标规划模型，其模型建立如下：

Qij≥0 i=1，2，…，m，j=1，2，…，n

2 模型求解

模型(1)为模糊多目标规划模型，直接求解的难度很大。本文采用的处理方法是先将模糊参数确定化，即将(1)转化为确定型多目标规划，再求解多目标规划。

2.1 模糊数据确定化

不确定分布函数也可作为隶属度函数，故本文采用不确定分布函数与隶属度函数来将模糊数据确定化。

(2)

首先，分别针对销售地的商品购买成本及运输时间对货物流通之前的数据进行统计，获得数据并计算其不确定分布函数为：

(3)

(4)

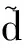
(5)

(6)

(7)

故(1)可转化为多目标规划：

(8)

2.2 求解多目标规划

对于确定型多目标规划的求解方法主要有四种，第一种是通过加权求和的方法将多目标规划转化为单目标规划再求解，第二种是采用maxmin方法将多目标规划转化为单目标规划再求解，第三种是采用遗传算法直接求解多目标规划，第四种是采用神经网络直接求解多目标规划。前两种算法都是致力于将多目标规划转化为单目标规划进行求解，操作简单，计算复杂度低，会得到确定的解，但会牺牲解的多样性。后两种算法，可求得多目标规划的最优解，会得到多样性的解，缺点是无法得到确定的解，需要从最优解中寻找合适的解，计算复杂度高，且当目标函数的个数超过三个时，求解难度较大。针对本文所转换而得到的多目标规划(8)，其中含有五个目标函数，故采用前两种方法求解更加合适。而加权求和法，权重需要在求解之前明确给出，而权重数是由研究者根据自身经验得到的，有很强的主观性，并且权重的取法会直接影响到最优解的求取结果。而maxmin法中没有主观参数，更加简单有效。综上所述，本文采用maxmin法求解多目标规划。

将(8)转化为如下单目标规划：

minλ

s.t. λ≥φz(x)

λ≥φt(x)

λ<1

Qij≥0

(9)

3 算例说明

台湾某公司主要商品为软饮料及低温食品。近期，该公司准备开发东南亚市场并增加其在中国市场所占的比重。该公司的茶饮料有四个主销售地：台中市、花莲市、高雄市和台北市。该公司的生产基地位于彰化市、斗六市和新竹市。表1给出了该公司的基本交通数据。表2给出了三个生产基地的生产数据。

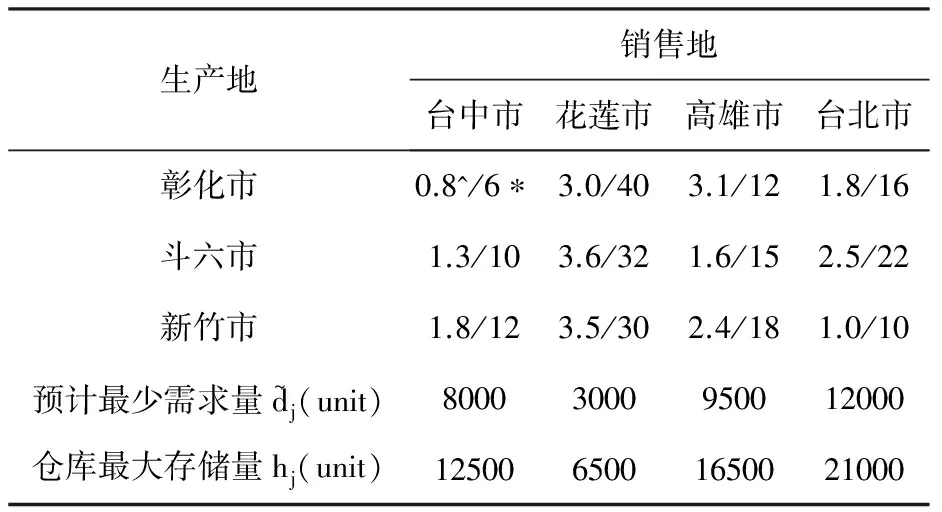
表1 交通数据

*注：“^”为商品运输费用cij($/unit)；“*”为商品运输时间tij(h/unit)

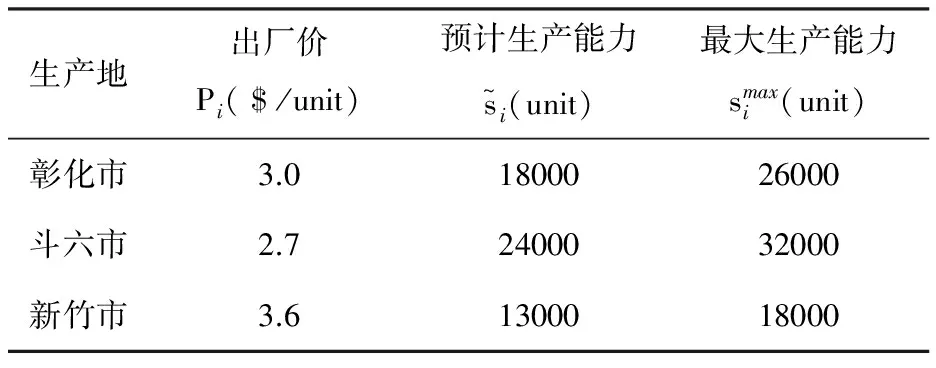
表2 生产数据

将上述数据带入模型(1)中，并转换为模型(9)，然后应用lingo10软件对现行规划进行求解，可得到运输方案如表3所示。

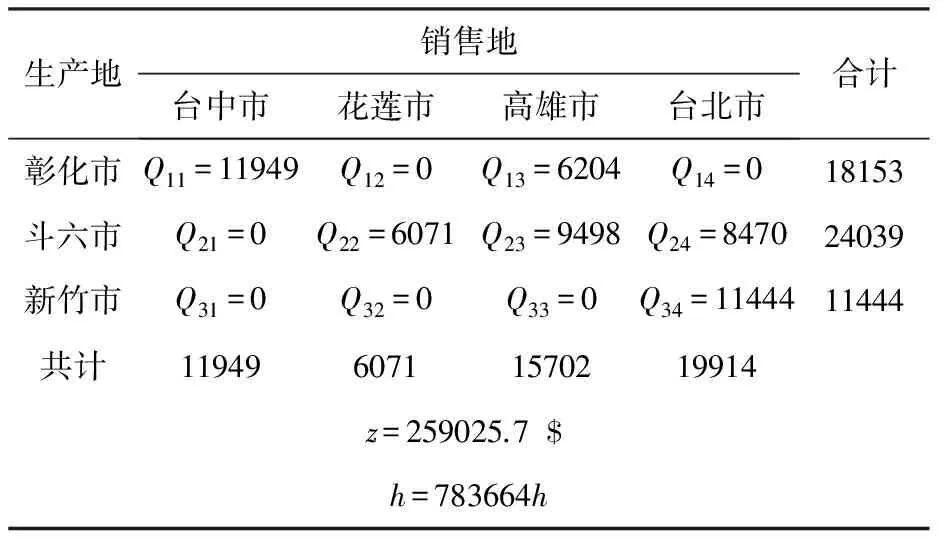
表3 计算结果

4 结语

本文以最少交通时间与运输成本为目标，建立了生产-销售的模糊双目标交通运输模型。该模型中包含五个约束，分别为三个不确定约束及两个确定性约束。其次，通过引进不确定分布函数、隶属度函数与maxmin法将该模糊多目标规划模型转换为确定型多目标规划模型，并进一步转换为单目标线性规划模型，并使用lingo软件对该单目标线性规划模型进行求解。最后，通过一个实例来验证本文所提模型与求解方法的有效性和可行性。在今后的研究中，应尽可能增加对转运问题的考虑。

[1] 韩伯棠.管理运筹学[M].北京:高等教育出版社,2015:135-167.

[2] ZIMMERMANN H J.Fuzzy programming and linear programming with several objective functions[J].Fuzzy Sets and Systems,1978,1(1):46-55.

[3] LAI Y L,HWANG C L.Fuzzy Multiple Objective Decision Making:Methods and Applications[M].Berlin:Springer-Verlag,1994.

[4] LAI Y L,HWANG C L.Possibilistic linear-programming for managing interest-rate risk[J].Fuzzy Sets and Systems,1993,54(2):135-146.

[5] LI X Q,ZHANG B,LI H.Computing effcient solutions to fuzzy multiple objective linear programming problems[J].Fuzzy Sets and Systems,2006,157(10):1328-1332.

[6] SELIM H,OZKARAHAN I.A supply chain distribution network design model:an interactive fuzzy goal programming-based solution approach[J].International Journal of Advanced Manufacturing Technology,2008,36(3):401-418.

[7] WERNERS B.Aggregation models in mathematical programming[M]//MITRA G,GREENBERG H J,LOOTSMA F A,et al.Mathe-matical Models for Decision Support.Berlin:Springer-Verlag,1988:295-305.

[8] CHANAS S,DELGADO M,VERDEGAY J L,et al.Interval and fuzzy extensions of classical transportation problems[J].Transportation Planning and Technology,1993,17(2): 203-218.

[9] LIU S T,KAO C.Solving fuzzy transportation problems based on extension principle[J].European Journal of Operational Research,2004,153(3):661-674.

[10] ZADEH L A.Fuzzy sets as a basis for a theory of possibility[J].Fuzzy Sets and Systems,1978,1(1):9-34.

[11] LIANG T F.Distribution planning decisions using interactive fuzzy multi-objective linear programming[J].Fuzzy Sets and Systems,2006,157(10):1303-1316.

[12] WATADA J.Fuzzy portfolio selection and its applications to decision making[J].Tatra Mountains Mathematics Publication,1997(13):219-248.

[责任编辑、校对：周 千]

Fuzzy Multi-objective Programming for Transportation Planning

LIURui,LIHua,LIYu-meng

(Faculty of Science,Xi′an Aeronautical University,Xi′an 710077,China)

From the perspective of sellers, this paper proposed a fuzzy multi-objective model for transportation planning.The aims of the proposed model are to minimize the transportation time and cost,which is under the condition that the retail purchases of sellers should meet the market demand and must not exceed the maximum inventory;the sum of the retail purchases of sellers should not exceed the estimated output of producers and must not exceed the maximum output;the sum of purchase cost and transportation cost of goods should not be higher than the budget cost.Then,the fuzzy data are described by introducing the uncertain distribution function and membership function,and the model is solved by maxmin method.At last,an example of a company in Taiwan is given to illustrate the effectiveness and feasibility of the proposed model and solving method.

fuzzy multi-objective programming;uncertain distribution function;membership function;maxmin method

2017-04-10

刘睿(1984-)，女，陕西西安人，博士，讲师，主要从事模糊多目标规划的应用与算法研究。

022

A

1008-9233(2017)03-0069-04