南京市溧水区万元GDP用水量影响因子研究

曹惠娟 杨钟宇 周心刚

(南京市溧水区水务局， 江苏 南京 211200)

南京市溧水区万元GDP用水量影响因子研究

曹惠娟 杨钟宇 周心刚

(南京市溧水区水务局， 江苏 南京 211200)

本文研究了溧水区万元GDP用水量的影响因子，通过理论分析及专家咨询确定了14个影响因子，并构建评价指标体系。在收集溧水区2005—2015年各指标数据基础上，运用主成分分析和逐步回归的方法，建立溧水区万元GDP用水量与其影响因子的数学模型，找出5个最重要影响因子并进行分析总结。

万元GDP； 用水量； 影响因子； 分析

1 引 言

我国人均淡水资源占有量约2100m3，仅为世界平均水平的28%，目前全国城市有约2/3缺水，约1/4严重缺水，水资源短缺已成为制约我国社会经济持续发展的重要因素之一[1]。同时，我国水资源利用方式粗放、用水效率不高，万元GDP用水量约为世界平均水平的2.5倍[2]。

溧水区位于江苏省南京市南部，属缓丘漫岗地区，总面积1066.94km2，其中丘陵面积773.5km2(含岗土旁地)，占总面积的72.5%。全区受旱概率高，春、夏旱发生概率55%，伏秋旱发生概率85%；多年平均降雨量1089.3mm，蒸发量1038mm；多年平均地表径流总量4.22亿m3[3]。干旱年份, 只能靠河沟、库塘蓄水或从外区江、河引提水才能基本满足全区生产生活用水需要。随着经济和城市化的发展，用水问题日益凸显，人水矛盾更加尖锐。根据溧水区用水现状，以万元GDP用水量作为效率评价目标，研究水资源的利用效率问题，找出影响这一效率目标的关键因子并进行分析，对于深刻认识溧水区水资源问题，制定切合实际的水资源战略及政策具有重要的现实意义。

2 溧水区万元GDP用水量评价体系的构建

指标体系构建遵循全面性、客观性、可获得性的建立原则[4]，采用理论分析和专家咨询相结合的方法，根据溧水区的实际情况进行分析、比较、综合，在初步拟定的基础上，征询专家意见，并进行调整。

溧水区万元GDP用水量评价体系可分为人口因素、资源因素、经济因素、管理因素、利用因素五个方面，共14个影响因子组成(见表1)。

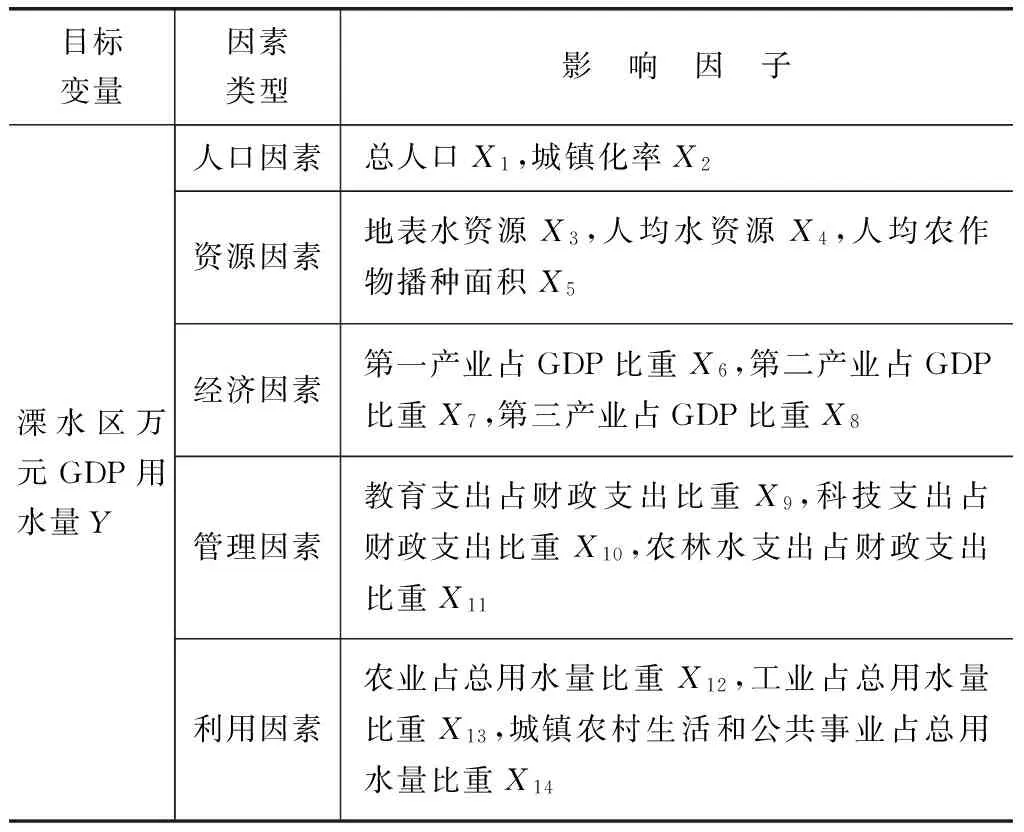
表1 溧水区万元GDP用水量影响因子

3 模型构建

为了量化研究影响因子与目标变量之间的关系，建立基于主成分分析的多元线性回归模型，为溧水区万元GDP用水量的调控提供参考依据。

3.1 主成分分析法

溧水区万元GDP用水量的影响因子较多，且因子间具有较强的相关性，直接建立回归模型，易形成模型的多重共线，造成虚假回归，增加了研究难度。为此，在回归分析之前采用主成分分析，在不损失或很少损失原有变量信息的前提下，将原多个彼此相关的变量用线性组合方法，转换为少数彼此独立的综合变量，起到 “降维”的作用，使回归模型不受变量多重共线性的影响。

3.2 多元线性回归分析法

多元回归是研究变量之间函数关系较为成熟的模型。利用主成分分析结果，把主成分作为自变量，万元GDP用水量作为因变量，采用逐步回归法建立回归模型。

3.3 影响因子换算

通过逐步回归法建立模型，自变量为主成分，但可视化程度不高，不方便直接研究，要根据14个影响因子在主成分上的投影系数，分解主成分获得14个影响因子的回归系数，得到新的回归模型。

4 模型计算

根据2005—2015年溧水县统计年鉴和南京市水资源公报[5-6]，收集溧水县2005—2015年万元GDP用水量及其影响因子数据(见表2和表3)。

表2 溧水县万元GDP用水量

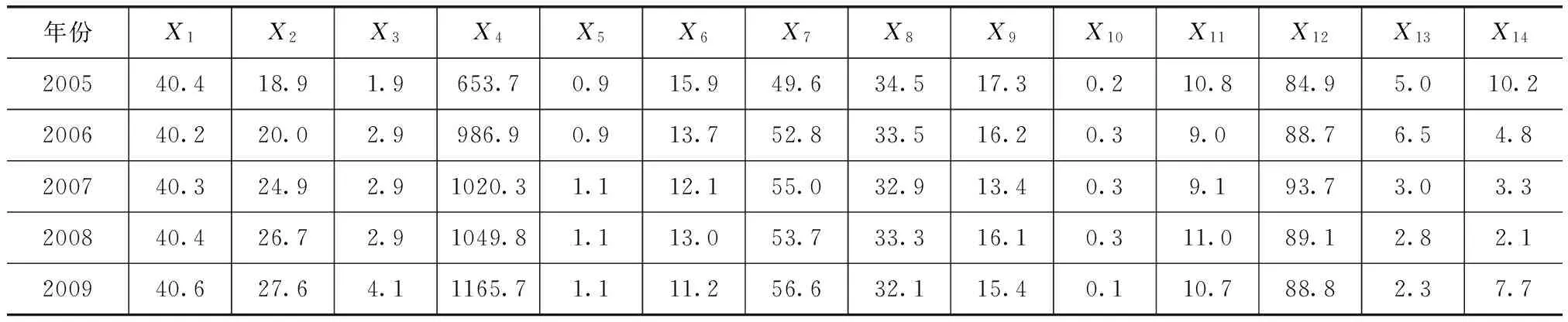
表3 溧水县万元GDP用水量影响因子数据

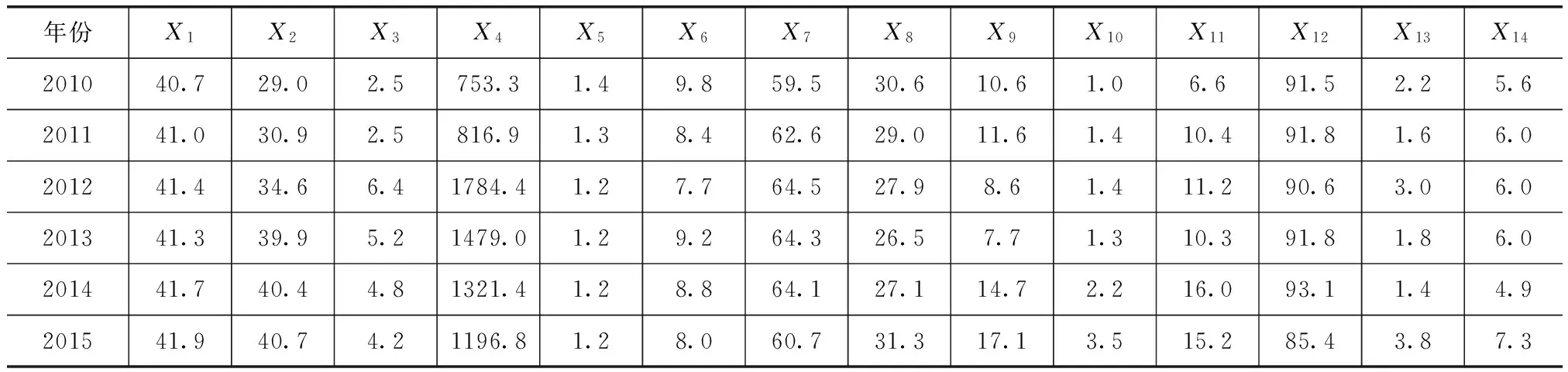
续表

4.1 数据标准化处理

鉴于影响因子之间的度量单位不同，取值范围差异大，首先考虑对数据的标准化处理，然后做主成分分析。

(1)

利用SPSS进行数据的标准化处理。

4.2 主成分分析

依据最大保留原始信息原则，对标准化后的数据运用SPSS做主成分分析。从表4看出，除地表水资源(0.599)、工业占总用水量比重(0.685)两因子在60%左右，其他各个原始因子都在75%以上。表5显示各主成分解释原始因子总方差，常规保证特征值大于1的基础上，当累计贡献率达到85%，就可保证主成分对原始信息的提取。本文研究中取3个主成分，集中了14个原始因子84.8%的信息，效果较好。

解释的总方差见表5。

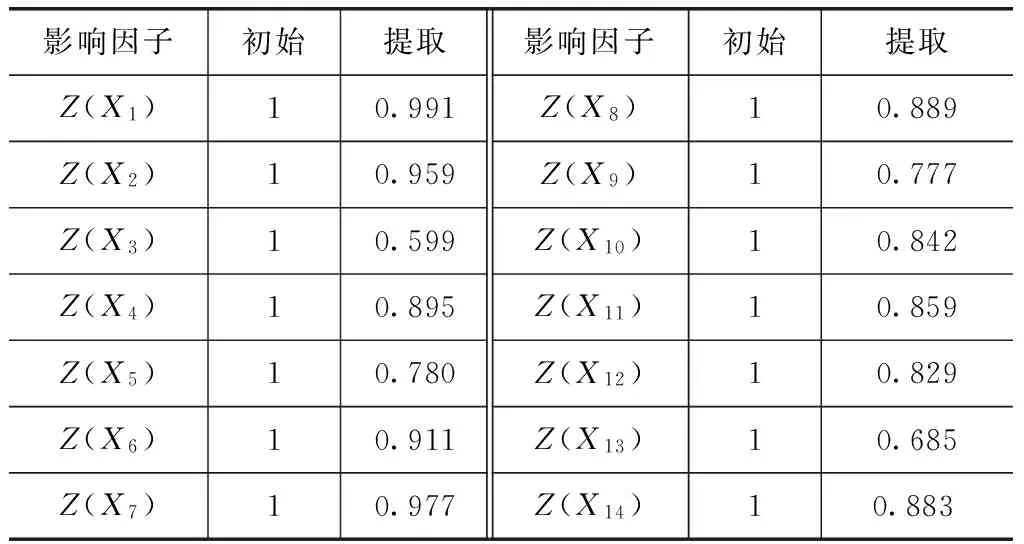
表4 标准化后因子方差提取

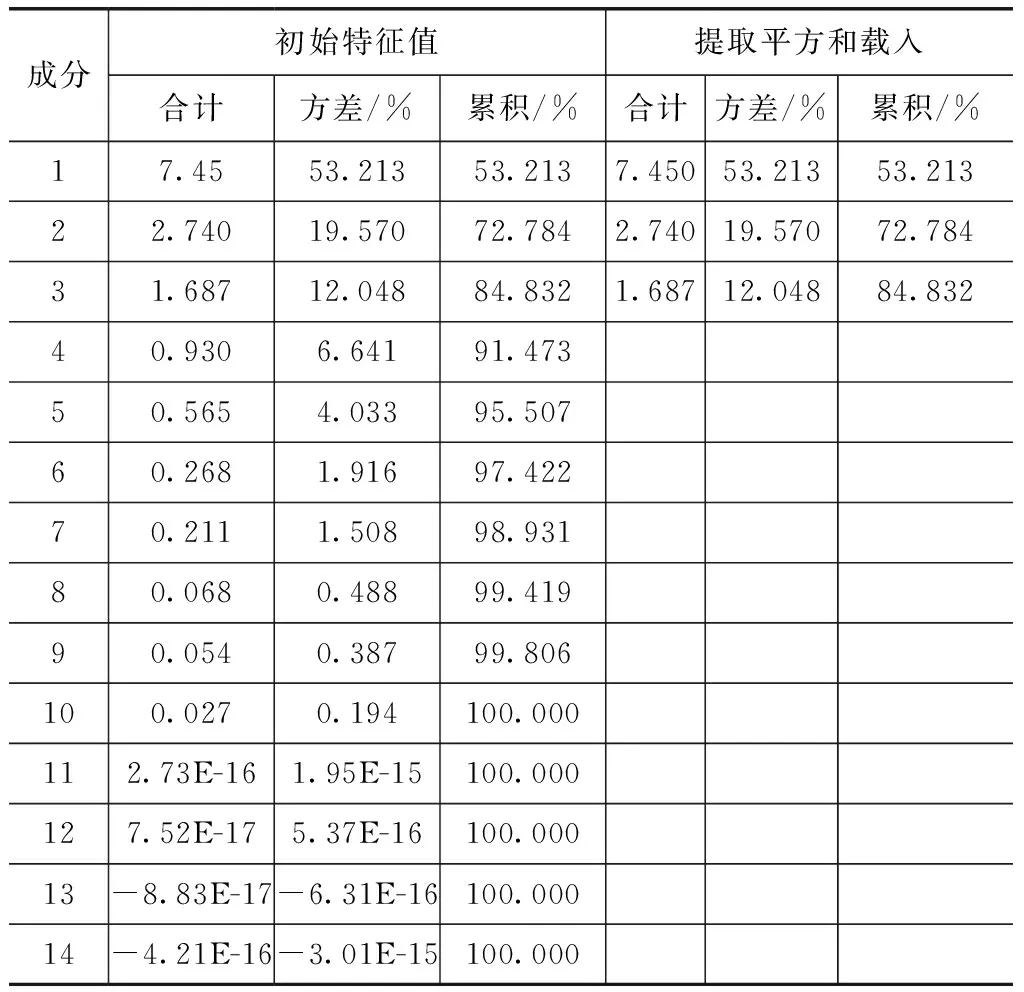
表5 解释的总方差

表6 主成分得分系数

主成分得分系数见表6。将影响因子代入，得到3个主成分(F1、F2、F3)表达式：

F1=0.204X1+0.171X2+0.149X3+0.103X4-0.053X5-0.085X6+0.072X7-0.051X8+0.116X9+0.218X10+0.284X11-0.103X12+0.041X13-0.011X14

F2=0.044X1-0.009X2+0.004X3+0.111X4-0.195X5+0.094X6-0.114X7+0.127X8+0.236X9+0.085X10+0.199X11-0.210X12+0.180X13+0.044X14

F3=-0.04X1+0.041X2+0.109X3+0.506X4-0.106X5+0.024X6-0.012X7+0.005X8+0.024X9-0.020X10+0.093X11+0.182X12+0.031X13-0.467X14

4.3 多元线性逐步回归分析

将3个主成分作为自变量，溧水区万元GDP用水量作为因变量，应用SPSS做多元线性回归分析，用逐步回归法建立模型。表7中模型调整R2=0.605说明模型对样本的拟合较好，F统计量的概率小于0.05, 说明模型对因变量影响显著。表8中回归系数T统计量的概率小于0.05，说明各自变量对应变量影响显著。DW检验和White检验：当α=0.05、n=11、k=2，查表dL=0.927、dU=1.324、χ2=5.96，则DW>dU，模型不存在自相关性；χ2>nR2=2.06，模型不存在异方差。

表7 回归模型

a. 预测变量：常量，F1；应变量(Y)：Z(万元GDP用水量)。

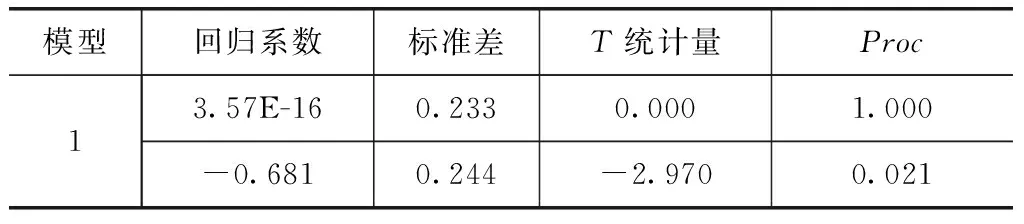
表8 回归系数

多元线性回归方程：

Y=-0.681F1

(2)

将F1带入式(2)，得出溧水区万元GDP用水量与其14个影响因子的回归方程：

Y1=-0.139X1-0.117X2-0.102X3-0.07X4+0.036X5+0.058X6-0.049X7+0.035X8-0.079X9-0.149X10-0.193X11+0.07X12-0.028X13+0.007X14

5 结 论

a. 从模型回归系数绝对值大小(表9)可看出，影响溧水区万元GDP用水量最大因子是农林水支出占财政支出比重(X11)、科技支出占财政支出比重(X10)，其次是总人口(X1)、城市化率(X2)和地表水资源(X3)5个影响因子。

表9 多元线性回归模型的回归系数绝对值

b. 影响溧水区万元GDP用水量最大5个因子分别集中于管理因素、人口因素和资源因素三方面。农林水支出占财政支出比重为影响作用最大的主因子，呈现正相关，因此从政府宏观管理角度，未来需要改善和调整农业与林业产业结构，提高农林用水效率，减少农林用水总量，从而降低万元GDP所需用水量；另外，当地政府仍需继续加大对水利事业的投入，完善规划、促进节水型社会建设、优化用水结构、加快工程建设、加强水资源保护；科技发展是用水效率提高的有效途径，继续加大科技投入，优化二、三产业布局和结构，淘汰高耗水高污染行业，满足溧水区人口、资源、环境与经济协调发展对水资源在时间、空间、数量和质量上的要求。

c. 城市化率和总人口是宏观经济发展的指标，在推进城市化进程中，政府加强对城乡空间的规划管理，把资源节约和环境保护放在城市化发展的重要战略地位，突出节地、节能、节水、节材，促进城镇的可持续发展。

d. 地表水资源是溧水区可用水资源的主体，在保持现状水资源开发利用格局和发挥现有供水工程潜力的情况下，考虑节水措施，抑制不合理用水需求，通过优化用水结构、加大过境水的利用、充分利用南京市区域辐射供水、加强中水回用等措施调整供水方案，进行水资源的合理配置。fffffd

[1] 云默.中国人均淡水资源占有量仅为世界平均水平的28%[EB/OL].(2012-02-13).http://news.china.com.cn/txt/2012-02/13/content_24625293.htm.

[2] 中国科学院可持续发展战略研究组.2007中国可持续发展战略报告——水:治理与创新[M].北京:科学出版社,2007.

[3] 曹惠娟,王平.溧水县水资源供需分析[J].水利经济，2012,30(2):46-48.

[4] 方诗标.农业灌溉水利用效率影响因素研究[D].扬州：扬州大学，2013.

[5] 溧水县统计局.溧水县统计年鉴(2005—2015)[M].溧水:溧水县统计局,2015.

[6] 南京水利局，江苏省水文水资源勘测局南京分局.南京水资源公报(2005—2015)[M].南京:南京水利局,2015.

[7] 曹惠娟，张启权，王平，等.水资源优化配置的探讨[J].江苏水利，2010(11):39-41.

Research on ten thousand Yuan GDP water consumption impact factors in Nanjing Lishui District

CAO Huijuan, YANG Zhongyu, ZHOU Xingang

(NanjingLishuiDistrictWaterDepartment,Nanjing211200,China)

The impact factors of ten thousand Yuan GDP water consumption in Lishui District are studied. 14 impact factors are determined through theoretical analysis and expert consultation. An evaluation index system is constructed. Principal component analysis and stepwise regression methods are applied to establish the mathematical model of ten thousand Yuan GDP water consumption and impact factors thereof in Lishui District on the basis of collecting index data in Lishui District from 2005 to 2015. Five most important impact factors are discovered, analyzed and summarized.

ten thousand Yuan GDP; water consumption; impact factor; analysis

10.16616/j.cnki.10-1326/TV.2017.06.009

TV213.9

A

2096-0131(2017)06- 0035- 04