结合投影与近邻操作的支持向量快速筛选方法

李蒙蒙，尚志刚，李志辉

(郑州大学 电气工程学院，河南 郑州 450001)

结合投影与近邻操作的支持向量快速筛选方法

李蒙蒙，尚志刚，李志辉

(郑州大学 电气工程学院，河南 郑州 450001)

为减少支持向量机(SVM)的计算负担,提高运算效率，并保证分类精度,提出一种结合投影与近邻操作的支持向量快速筛选方法.该方法利用Fisher投影轴的全局特性将其作为SVM最优分类面的近似法方向，在该方向快速筛除大量非支持向量，将分类边界附近的样本集作为备选支持向量集，同时为解决投影操作未考虑样本局部结构信息造成的误删支持向量的问题，结合近邻操作回选样本空间中备选支持向量的近邻样本更新扩充备选支持向量集，以该子集中的样本作为SVM的输入.在多个UCI标准数据集上的实验结果表明，该方法在充分保证分类精度的前提下有效降低了SVM的计算负担，具有较好的推广性.

支持向量机；支持向量；Fisher投影；k-近邻；快速筛选

0 引言

支持向量机(support vector machine，SVM)是建立在统计学习VC维理论和结构风险最小化基础上的机器学习方法，其学习过程实际是求解一个二次规划问题，需用到所有训练样本的Hessian矩阵，故遇到样本集较大的学习问题时，传统方法内存消耗过大且学习速度缓慢，从而影响了它的实用价值和推广.针对这一问题，近年出现了许多改进算法提高SVM对大样本集的学习速度.一种思路是改进优化方法，以Keerthi等提出的循环最近点算法[1]、Platt提出的序贯最小优化算法最具代表性.另一种思路是通过某种处理缩减样本集得到规模较小的替代集而又不影响分类精度，如文献[2-3]提出的局部支持向量机算法，利用K均值聚类生成的样本中心点集作为替代；文献[4]提出基于距离排序的快速支持向量机分类算法；文献[5]提出基于k-近邻法的快速训练算法；文献[6]提出了基于Fisher鉴别分析的训练样本缩减策略.上述算法筛除了冗余样本，减少了无谓运算，提高了运算速度.但由于数据压缩往往会误删一部分支持向量，破坏原分类边界，造成一定程度的精度下降.考虑到SVM确定的支持向量均靠近分类边界并最终决定最优分类面，而其他大量非支持向量则属于冗余样本，故如何在保持原样本集分类边界较完整的条件下，快速筛除与分类无关的非支持向量具有重要的研究价值.

为快速准确地筛除大量非支持向量，提高SVM确定支持向量的计算效率，笔者提出一种结合投影与近邻操作的方法，利用Fisher投影的全局特性，快速粗略地筛除大量远离分类边界的冗余样本以减少计算量，结合邻域选择可以保留数据局部结构信息的优势，进行样本回选以避免对支持向量的误删，保证分类边界信息的完整性.

1 支持向量机的原理与问题

SVM基于结构风险最小化理论在样本空间中构造最优超平面.对线性可分样本集，必然存在最优超平面保证在分类间隔最大的条件下正确划分所有训练样本，这同时保证了经验风险最小和结构风险最小，从而达到期望风险最小化[7—9].

设数据集中的两类样本分别可标记为{xi,yi},i=1,…,l，其中，l为样本的总数，yi为类别标签且yi∈{-1,1}.SVM的求解问题是一个对于不等式约束的条件极值问题，引入非负的拉格朗日系数αi，可表述为如下的拉格朗日方程：

(1)

将上式转化为较简单的“对偶”形式为：

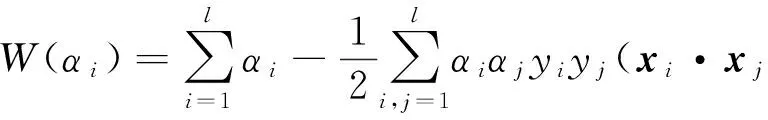
(2)

2 结合Fisher投影与近邻法的支持向量快速筛选方法

SVM中靠近分类边界的支持向量对确定最优分类面较重要，而远离边界的样本可视作冗余样本进行筛除.Fisher最佳投影轴可近似视为SVM分类面的法方向，故可将其引入SVM中快速筛除冗余样本以缩减样本集，从而更快筛选出支持向量.但由于Fisher投影侧重样本集的全局结构信息，而未考虑局部结构信息可能误删支持向量，故笔者拟采用结合投影和近邻操作的方法解决这一问题，以快速准确筛选出潜在支持向量.

2.1 Fisher投影筛除非支持向量

(3)

为求满足上式的投影方向w，引入拉格朗日乘子求解无约束极值问题，得到最佳投影方向：

(4)

所有样本向w投影得对应投影值，但这种向一维空间的特征压缩不像SVM考虑了分类面附近的局部结构信息，故推理知在此基础上筛除冗余样本会不可避免地误删一部分潜在支持向量.

笔者采用数值实验验证上述推理，Fisher投影筛除方法如下：对X中任一样本x，其投影表示为z=wTx.选取两类样本最靠近边界者的均值为基准点，记作z0，逻辑推理知远离z0的是非支持向量冗余样本，反之则更有可能是SVM确定的支持向量.记z0两侧投影点对应的原始样本集为X+和X-，分别计算它们与z0的距离，记：

(5)

(6)

其中，1，2，…,n1；1，2，…,n2是排序前的序号.

对D+和D-排序，以(1),(2),…,(k1),…,(n1)；(1),(2),…,(k2),…,(n2)作为排序后的新序号，记：

(7)

(8)

(9)

以Iris数据集为例做上述处理，结果见图1.其中l1为样本集X在Fisher最佳投影轴上的分布，l2为SVM确定的支持向量集S的分布，l3为用上述方法处理得到的备选支持向量集G的分布.

图1 仅采用Fisher投影筛除非支持向量的效果Fig.1 The effect of filtering out non-support-vector using Fisher projection only

从图1可看出，仅采用Fisher投影筛除冗余样本会误删部分支持向量，故需考虑G的扩充更新，为此引入k-近邻法从样本空间回选备选支持向量的近邻补充合并为新的备选支持向量集.

2.2k-近邻法回选扩充备选支持向量集

k-近邻法是基于距离的度量方法[13].采用欧氏距离作为确定近邻的测度，在原始样本空间中回选k个与备选支持向量距离最近的样本更新扩充备选集.遍历备选支持向量集G，对其中任一元素g，计算其与F中样本之间的距离，记：

dj=norm(g-Fj)={d1,d2,…,dj}.

(10)

对dj排序，记：d(1)≤d(2)≤…≤d(j)，设定近邻样本回选参数k(1≤k)，从中选取前k个较小值对应的样本，即距离g最近的k个样本组成回选更新集g*，合并所有备选支持向量的更新集作唯一化处理剔除重复样本，得到的合集记为G*，则G∪G*即为补偿更新后的备选支持向量集.

结合近邻操作回选更新备选支持向量集后的非支持向量筛除效果如图2所示，l4为采用上述方法更新备选支持向量集后的投影分布.

对比图1与图2表明对G进行上述回选更新后可更准确地提取潜在支持向量，进而更好地保留数据集的边界信息，为确定最优分类面提供可靠支持.笔者将这种结合Fisher投影和k-近邻法快速筛选支持向量的方法称为Fisher Projection-kNearest Neighbor_Support Vector Filter，记作FP-kNN_SVF.

图2 结合近邻操作回选更新后的非支持向量筛除效果Fig.2 The effect of filtering out non-support-vector combining nearest neighbor selection with Fisher projection

2.3 FP-kNN_SVF方法的步骤

笔者提出的FP-kNN_SVF方法流程见图3.具体步骤表述如下：

(1) 输入数据集，设定筛除率r和近邻参数k；

(2) Fisher投影得到投影值并计算基准点；

(3) 计算各投影值与基准点的距离并排序，按r由式(9)筛除非支持向量得到备选支持向量集；

(4) 计算每个备选支持向量与筛除样本间的距离并排序，按k回选备选支持向量的近邻更新备选支持向量集，得到新的备选支持向量集.

3 数值实验与结果分析

为考察FP-kNN_SVF方法在不同数据集上的应用性能，包括其计算速度、分类精度与鲁棒性，以及参数r和k对实验结果的影响，笔者开展了相关数值实验.文中所有计算均采用MATLAB软件编程实现，实验条件为Intel(R) Pentium(R) D CPU 3.20 GHz/4.00 GB/ Windows XP/MATLAB 8.0.

图3 FP-kNN_SVF方法流程图Fig.3 The flow chart of the FP-kNN_SVF method

3.1 FP-kNN_SVF方法的有效性评估

考虑在样本数量和特征数量上多样化的条件下对比结果差异，选取UCI数据库中6个数据集进行实验.采用交叉互验证，随机选取每个数据集70%的样本作训练集，30%作测试集，随机抽样10次分别实验，以10次的平均结果作为3种方法的最终结果加以比较，分类效果如表1所示.(其中Iris和Wine数据集均原有3类，分别将两者的第一类作为正类，其余两类合并作为负类.)

实验结果表明：①F_SVM和笔者提出的F-k_SVM都可以快速筛除样本，并较大幅度降低运行时间，F_SVM运行时间只占SVM的28%以下，F-k_SVM的运行时间也都只占SVM的64%以下，F_SVM在的表现更突出；②3种方法中，F_SVM的分类精度最低，而F-k_SVM的分类精度高于F_SVM，与原始SVM相当甚至高出SVM，且其鲁棒性也高于其他两种方法.

综合以上两点说明:F-k_SVM在不同数据集上均有良好的表现，能够充分保证分类的准确性和鲁棒性，并提高计算效率.

表1 SVM、F_SVM和F-k_SVM在6种数据集上的分类效果比较

注：不筛除样本的方法记作SVM，文献[8]中仅采用Fisher投影筛除样本后结合SVM的方法记作F_SVM，笔者提出的FP-kNN_SVF方法结合SVM记作F-k_SVM.

3.2 筛除率r对结果的影响

对于样本筛除率r的选择，笔者以Australian 数据集为例，分别令r=10,30,50,70,90，各进行10次重复随机抽样实验，记录10次的平均运行时间与分类精度，取k=5，结果如图4所示.

图4 不同r值下的实验结果(k=5)Fig.4 The test results with different r (k=5)

图4表明,平均运行时间随r的增大而降低，这是由于r越大，保留的需处理样本越少，运算时间也对应降低；r为10～70时平均分类精度变化不大，而r为90时精度明显下降，这是由于筛除了过量样本造成支持向量损失严重引起的.故针对不同数据集，应根据其实际的数据结构设置不同的r以获得时间与精度之间最好的折衷.

3.3 参数k对结果的影响

对近邻参数k的选择，笔者仍以Australian 数据集为例，分别令k=3,5,7,9,11,13,15，各进行10次随机抽样实验，记录平均运行时间与分类精度，r为25和90时的结果如图5、图6所示.

图5 不同k值下的实验结果(r=25)Fig.5 The test results with different k (r=25)

图6 不同k值下的实验结果(r=90)Fig.6 The test results with different k (r=90)

图5、图6的结果表明：r取25时， 平均运行时间和分类精度随k的变化仅发生较小波动，即k对结果无较大影响；r取90时，平均运行时间和分类精度随k的变化均呈上升趋势，即此时k对结果产生了一定的影响.这是因为，r取25时样本筛除结果相对安全，较多支持向量被保留，而近邻回选得到的多数结果相互重合，造成不同k值下更新后的备选支持向量集相差不大，故实验结果波动不大；而r取90时由于筛除过程过于贪婪，误删了一部分支持向量造成分类精度的下降，而通过逐渐增大k，可以扩充备选支持向量集恢复已被破坏的数据结构，这一方面增加了分类的准确性，但也因运算量的增加造成运行时间的上升.故实际操作中应根据不同的r下的结果确定k的取值以改善算法性能，即r取值合适时应尽量选取较小的k减少运算；r取值过大时应尽量选取较大的k值以保证精度.

4 结论

笔者利用Fisher投影的全局性质与k-近邻法保留局部结构信息的作用，提出了一种结合投影与近邻操作的支持向量快速筛选新方法，通过在实际数据集上的应用得到如下结论：

(1)笔者提出的F-k_SVM可以快速准确筛选支持向量以提高运行速度，并能获得更高的分类精度和鲁棒性，有效解决了F_SVM精度下降的问题，具有较好的推广性.

(2)对不同数据集设置合适的筛除率r可同时保证较少的运行时间与较高的分类精度.

(3)设定不同的筛除率时，应根据实际情况进行参数k的选择以获得较好的实验效果.

笔者提出的F-k_SVM基于线性层面解决大样本集问题，扩展到核空间可能会更好解决复杂非线性问题；另外，文中筛除率r是事先设定的，如何根据数据集的结构自适应地确定r也很有意义,故上述两点将成为笔者下阶段的主攻方向.

[1] KEERTHI S S, SHEVADE S K, BHATTACHARYYA C, et al. A fast iterative nearest point algorithm for support vector machine classifier design[J]. IEEE transactions on neural networks, 2000, 11(1): 124-136.

[2] 田新梅,吴秀清,刘莉. 大样本情况下的一种新的SVM迭代算法[J]. 计算机工程, 2007, 33(8): 205-207.

[3] 浩庆波,牟少敏,尹传环,等. 一种基于聚类的快速局部支持向量机算法[J]. 山东大学学报(工学版), 2015, 45(1): 13-18.

[4] 胡志军,王鸿斌,张惠斌. 基于距离排序的快速支持向量机分类算法[J]. 计算机应用与软件, 2013, 30(4): 85-87.

[5] 孙发圣,肖怀铁. 基于K最近邻的支持向量机快速训练算法[J]. 电光与控制, 2008, 15(6): 44-47.

[6] 饶刚,刘琼荪. 基于Fisher鉴别分析的支持向量机训练样本缩减策略[J]. 计算机工程与应用, 2012, 48(3): 156-157.

[7] 顾亚祥,丁世飞. 支持向量机研究进展[J]. 计算机科学, 2011, 38(2): 14-17.

[8] NANDHINI K, SANTHI B. Retrospection of SVM classifier[J]. Journal of theoretical and applied information technology, 2012, 38(1): 83-88.

[9] 张震,张英杰. 基于支持向量机与Hamming距离的虹膜识别方法[J]. 郑州大学学报(工学版), 2015, 36(3): 25-29.

[10]VAIDYA J, YU H, JIANG X. Privacy-preserving SVM classification[J]. Knowledge & information systems, 2008, 14(2): 161-178.

[11]张炎亮,刘阳,王金凤. 基于改进SVM的煤矿水灾害救援组织系统可靠性预测[J]. 郑州大学学报(工学版), 2015, 36(3): 115-119.

[12]陈立江,毛峡, ISHIZUKA M. 基于Fisher准则与SVM的分层语音情感识别[J]. 模式识别与人工智能, 2012, 25(4): 604-609.

[13]曹根,葛孝堃,杨丽琴. 基于K-近邻法的局部加权朴素贝叶斯分类算法[J]. 计算机应用与软件, 2011, 28(9): 267-268.

Fast Method to Filter Support Vectors Combined with Operation of Projection and Nearest Neighbors’ Selection

LI Mengmeng, SHANG Zhigang, LI Zhihui

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

To reduce computational burden and improve operation efficiency of support vector machine (SVM) while ensuring classification accuracy, a fast method to filter support vectors combined with operation of projection and nearest neighbors’ selection was proposed. Considering the global characteristics of Fisher projection, it could be viewed as the approximate normal directions of SVM optimal hyperplane and filtered out a large number of non-support-vectors in this direction. The samples near the classification obtained boundary were regarded as alternative support vectors set. Neighborhood operation was combined to solve the problem that some support vectors might be filtered out mistakenly regardless of the local structure information. A number of nearest neighbors of the alternative support vectors were selected backward from the samples space to update and expand the alternative support vectors set. The sets was treated as the SVM input. The experimental results on several UCI standard data sets showed that the fast method had good generalization performance and reduced the computational burden effectively under the premise of fully guaranteed classification accuracy.

SVM; support vector; fisher projection;k-nearest neighbor; rapid filter

2016-06-08；

2016-08-18

国家自然科学基金资助项目(U1304602;61473266),河南省高等学校重点科研资助项目(15A120016)

尚志刚(1975— )，男，甘肃兰州人，郑州大学副教授，博士，主要从事生物医学信息与模式识别研究，E-mail：zhigang_shang@zzu.edu.cn.

1671-6833(2017)03-0049-05

TP391.4

A

10.13705/j.issn.1671-6833.2016.06.003