积分变换法在求解静电场边值问题中的应用

齐 宁， 许哲翔， 张 强

(天津大学 1. 求是学部 2. 电气与自动化工程学院，天津 300072)

积分变换法在求解静电场边值问题中的应用

齐 宁1， 许哲翔2， 张 强2

(天津大学 1. 求是学部 2. 电气与自动化工程学院，天津 300072)

静电场边值问题一般采用直接积分法、分离变量法、镜像法等常规方法求解析解。本文基于积分变换法求解微分方程的思想，运用傅里叶变换等积分变换方法，得出在一定条件下采用积分变换法求解静电场边值问题具有可行性和简便性，为求解相似问题探索出一条新的途径。

静电场边值问题；积分变换法；有限傅里叶变换

0 引言

电磁场的边值问题在电磁场理论中具有重要的地位，而静电场的求解是电磁场教学中的首要内容。在“工程电磁场导论”中，静电场边值问题的解法主要有两大类：解析法和数值法，其中解析法又包括直接积分法、分离变量法、镜像法和电轴法[1]。由于镜像法和电轴法只适用于求解特殊边界条件下的静电场边值问题，而直接积分法和分离变量法在某些问题下求解过程较为复杂。若能将静电场中的泊松方程或拉普拉斯方程中的自变量个数减少一个，即将原来的偏微分方程变换为常微分方程，再通过反演得到原始问题的解，将大大降低求解难度。

基于这一思想，本文采用积分变换法求解静电场边值问题，针对多种边界条件情况，运用积分变换方法，使问题的求解过程由繁到简。

1 积分变换简介

积分变换是将一个函数通过积分运算变换成另一个函数，主要用来求解复杂的微积分方程，使得求解过程简单化。常见的积分变换有两种：傅里叶(Fourier)变换和拉普拉斯(Laplace)变换，通过这些变换方法，并结合反演公式和变换的一些基本性质，求得目标函数的解析式。

本文主要运用傅里叶变换来求解静电场边值问题。

2傅里叶与拉普拉斯变换的分析与应用

2.1 傅里叶变换与拉普拉斯变换的分析

理论上拉普拉斯(Laplace)变换对于函数性质的要求弱于傅里叶(Fourier)变换。拉普拉斯(Laplace)变换可以用于含时间参数的偏微分方程定解问题的求解，适合求解时变场的边值问题，对于系数与时间t无关的偏微分方程，通过积分变换可以减少自变量t，变换偏微分方程为常微分方程，再通过反演，即求逆变换求得原函数，而逆变换的难易度取决于具体问题。

傅里叶(Fourier)变换是对空间变量进行积分变换，根据空间变量的变化区间，可选用正弦变换、余弦变换(自变量变化区间为半无界区域)，或者有限正弦和余弦变换(适用于自变量变换区间有界的情况)。

由于实际问题中区间绝大部分为有界情况，因而采用有限的傅里叶变换更具有实际意义。有限傅里叶变换分为有限正弦和有限余弦变换，简写为DST和DCT。有如下表达式：

DST：

n=1,2,… (1)

反演后得到函数表达式为

(2)

DCT：

(3)

反演后得到函数表达式为

(4)

对于多元函数，以二元函数为例，对φ(x,y)中的x进行有限正弦变换得到Φ(x,y)。

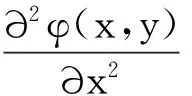
n=1,2,… (5)

n=1,2,… (6)

同理也可以得到相关有限余弦变换的表达式:

(7)

(8)[4]

可以看到对应正弦变换需要的边值条件为第一类边值条件，而对于余弦变换需要第二类边值条件，所以应当根据具体问题选择适当的方法，原则如下[3]：

(1)所涉及的自变量的变化区间应该与该变换的区间要求一致；

(2)未知函数的该种积分变换存在；

(3)要求函数f(x)及其各项导数的在该变换下有简单的代数关系；

(4)所涉及的未知函数及其低阶导数的特殊值正好由定解条件给出。

2.2 一道经典电磁场问题的求解

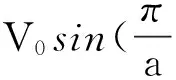
根据已知条件，可以得到金属槽内的电势满足拉普拉斯方程，并且得到所求场域的第一类边界条件：

(9)

φ(x,y)|x=0=0

(10)

图1 接地金属槽的截面

φ(x,y)|x=a=0

(11)

φ(x,y)|y=0=0

(12)

(13)

(1)采用分离变量法求解

设φ(x,y)=φ1(x)φ2(y)，代入式(9)得到

(14)

解之，得电位函数的一般形式：

φ(x,y)=(A0+B0x)(C0+D0y)

(15)

采用待定系数法，由边界条件式(10)、式(11)、式(12)得到

(16)

再将式(13)代入得

(17)

最终得到电势分布

(18)

通过这一例子可以看出采用分离变量法求解静电场简单边值问题的复杂性。

(2) 采用积分变换法求解

对原问题的边值问题的变量x进行有限正弦变换，并将边值条件代入化简可得到：

(19)

(20)

C2=-C1=0n=2,3,…

(21)

得到电势的最终表达式：

(22)

通过以上计算可以发现离散的傅里叶变换与分离变量法在本质上是相似的，都需要把电势函数进行离散化处理，但是通过比较可以发现离散的傅里叶变换能够大大简化表达式中系数的计算，相比之下分离变量法需要确定系数太多，容易造成分析错误。

3 积分变换法求解静电场边值问题

的局限性探索

问题：如图2所示，在均匀外电场E0中，有一半径为a、介电常数为ε2的无限长均匀介质圆柱体，其轴与E0垂直，柱外充满介电常数为ε1的均匀介质。求柱内柱外的电位分布。

图2 均匀外电场中的介质圆柱体

(1)采用分离变量法求解[1]

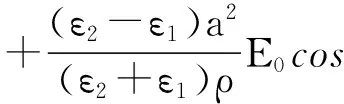
(23)

(24)

(2)采用傅里叶变换求解

首先列写出边值问题的方程组：

(25)

经过化简得：

(26)

其中C1,C2,A1,A2为待定常数，可以发现，由于边值条件带有三角函数，则其像函数会出现广义函数δ(t)，这样常数的求解可能比较特殊，对分离变量法得到的解进行傅里叶变换，发现它的像函数是带有广义函数，而傅里叶变换求解的表达式中未待定函数为指数形式，由于方程两边都是无界的，说明常数项可能带有广义函数的形式，甚至无法求解。对于这种情况可以通过Matlab进行处理或者直接进行数值计算。因此，如果边值条件带有需要变换参量的三角函数，可利用积分变换法化简为常微分方程再利用计算机辅助求解。

4 结语

积分变换法与分离变量法相比，在求解一定条件下的静电场边值问题能够大大降低求解难度。对不同的边界条件问题，针对性地采用傅里叶变换或拉普拉斯变换等积分变换方法，能够有效解决一些静电场的边值问题，但各种解法都有一定的局限性。本文为求解静电场边值问题提供了一个新的思路，扩充了静电场边值问题的求解方法。

[1] 冯慈璋,马西奎. 工程电磁场导论[M]. 北京:高等教育出版社,2000.6

[2] 彭丽,张玲玲,任淑青,等. 积分变换与场论[M]. 北京:中国铁道出版社,2015.8

[3] 吴崇试. 数学物理方法[M].2版. 北京：北京大学出版社,2003,12.

[4] 段汕. 有限Fourier变换在偏微分方程中的应用[J]. 武汉:中南民族学院学报(自然科学版), 1999, 18(4):62-67

The Application of Integral Transform Method to Solve the Boundary Value Problem of Electrostatic Field

QI Ning1，XU Zhe-xiang2，ZHANG Qiang2

( 1.SchoolofQiushiHonorsCollege,TianjinUniversity,2.SchoolofElectricalEngineering&Automation,TianjinUniversity,Tianjin300072,China)

Generally, the solving methods for boundary value problem of electrostatic field to get analytical solutions are direct integral method, separation of variables, image method and so on. Applying integral transform method for solving differential equations, this paper has used Fourier Transform and other integral transform methods, and reaches a conclusion that under certain conditions the application of integral transform method to solve the boundary value problem of electrostatic field is feasible and simple, and explores a new way to solve similar problems.

boundary value problem of electrostatic field; integral transform method; finite Fourier transform

2016-06-05;

2016-09- 01

齐 宁(1996-)男，在读本科生，研究方向为电工电子专业，E-mail:tjuqining@163.com 许哲翔(1996-)男，在读本科生，研究文向为电气工程及其自动化专业，E-mail: 670414xujj@gmail. com 张 强(1979-)，男，博士，讲师，主要从事电路和电磁场教学工作，E-mail:zhangqiang@tju.edu.cn

G642.4

A

1008-0686(2017)02-0079-04