基于遗传算法的智能电能表配送路径优化研究与应用

田 广，罗 蓬，刘朋辉，李铁成

(1.国网河北省电力公司，石家庄 050021；2.国网河北省电力公司电力科学研究院，石家庄 050021)



基于遗传算法的智能电能表配送路径优化研究与应用

田 广1，罗 蓬2，刘朋辉1，李铁成2

(1.国网河北省电力公司，石家庄 050021；2.国网河北省电力公司电力科学研究院，石家庄 050021)

针对省级计量中心超大规模智能电能表集中配送业务需求，提出一种基于遗传算法的智能电能表配送路径优化选择方法。以河北省南部电网二级库房配送路径规划应用为例，在车辆载容、电能表需求量、最大里程数等约束条件下，建立集中配送业务的规划路径数学模型，以配送成本最小化为目标，实现了配送路径的全局寻优，为省级计量中心建立经济高效的智能电能表配送方案提供了科学的依据，仿真实验的结果验证了该方法的有效性。

智能电能表；配送；遗传算法；路径优化

0 引言

城市配送系统是多约束条件路径规划问题的一个典型应用[1]，其概念是在一个有限的区域范围内，通过统筹管理和动态调度的物流配送路线，将货物送至有需求的地点的综合服务系统，核心业务包括生产调度、交通运输、货物存储以及信息化管理等[2]。在城市配送体系的优化管理研究中，配送中心和运输线路的集成管理与优化是一个首要问题，而供电企业电能表配送业务是城市配送系统车辆路径优化问题(Vehicle Routing Problem，VRP)的一个典型应用[3]。

对于省级计量中心，合理安排好配送路线，不仅可以极大地节约成本，而且还可以大幅提高效率。目前，针对该问题的研究已成为行业热点，文献[4]采用启发式算法对一些相对简单的VRP问题进行了探索，文献[5-6]采用逐次逼近的扫描法寻找配送车辆调度优化方案。然而上述方法均无法求得问题的最优解，且算法鲁棒性较差，当编码方案较为简单时，扫描类算法求解质量劣化严重。以下针对省级电力计量中心智能电能表集中配送的路径选择问题，建立涵盖全部二级库房的配送规划路径数学模型，采用遗传算法(Genetic Algorithm，GA)的选择、交叉、变异等算子对目标函数进行规划[7]，获取适应性强的选择方案并将其优秀特征遗传到下一代，最终获得最优配送路线，为建立经济高效的智能电能表配送方案提供了科学的依据。

1 遗传算法简述

遗传算法是目前较为常用的一种全局优化算法，通过模仿自然界中生物进化的规律来建立寻优方案，采用概率化的寻优方法，能够自动获取和指导优化的搜索空间。该算法的特点是可靠性高、收敛速度快，而且可以不依赖于数学模型的梯度信息，是一种自适应全局随机优化方法。

在遗传算法中，染色体对应的是数据或数组，通常由一维的串结构数据来表示，串上各个位置对应基因取值。基因组成的串就是染色体，或者称为基因型个体。一定数量的个体组成群体，群体中个体的数目称为种群大小，或称为种群规模。各个体对环境的适应程度称为适应度(fitness)。遗传算法的基本运算过程如下。

a. 编码。遗传算法在进行搜索之前，需要将解空间转换到遗传空间。编码就是将实际的解空间映射为相应的可以被遗传算法处理的遗传空间的过程，遗传算法的编码就是解的遗传表示，它是应用遗传算法解决问题的第一步。

b. 初始化种群。遗传算法解决问题时，需要随机产生N个初始串并进行迭代搜索，初始串的集合及每次迭代生成的一代新串数据就构成了一个种群。遗传算法以这N个串结构数据构成的种群为初始种群，即由该初始种群作为起始点开始进化。

c. 适应度评价。适应度是度量种群中个体在优化计算中可能达到或接近于最优解的优良程度，用来评价种群中个体的优劣，是遗传操作的依据，一般是通过将目标函数映射成适应度函数来对其进行计算并评价。

d. 选择运算。选择运算是在适应度评价的基础上进行的，种群中个体的适应度决定了被选择的概率，适应度越高的个体被遗传到下一代的概率较高。选择过程充分体现了达尔文的“适者生存”原则，常见和应用较多的选择策略是轮盘赌选择。

e. 交叉运算。交叉运算也称为“基因重组”，在遗传算法中起着非常关键的作用，决定了遗传算法的全局搜索能力。交叉运算是对群体中的个体进行随机配对，将2个配对的个体按某种方式相互交换其部分基因，形成2个新个体。

f. 变异运算。变异运算是指个体编码中的某些基因用其它等位基因来替换，产生新个体的操作。变异运算主要为了改善遗传算法的局部搜索能力，维持群体多样性，防止出现早熟现象。由于在生物界中发生变异的情况很少，所以变异概率一般较低。

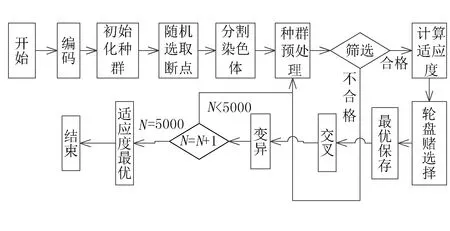
图1 遗传算法流程

2 智能电能表配送路径规划模型

根据河北省南部电网智能电能表配送实际情况，将配送车辆路径规划抽象为典型数学模型，并作如下假设：

a. 智能电能表配送过程专指从省级计量中心一级库房到各市县供电公司二级库房的过程；

b. 只有省计量中心一个一级库房，每辆车均从省计量中心出发，完成本车路径上配送任务后直接返回省计量中心；

c. 只有一种车型，每辆车的载容已知，单个供电公司的需求量不超过单车载容；

d. 一级库房与二级库房的地理坐标已知，即省计量中心与地市供电公司之间的距离已知；

e. 二级库房的智能电能表配送需求只能由一辆车配送，每辆车所走的路线不重复；

f. 每辆配送车根据智能电能表需求单位在做好区分标示的前提下可以进行混装；

g. 每辆配送车的最大行驶距离已知，不能超过该最大里程；

h. 配送成本与行驶里程呈正比关系，车辆行驶路径决定车辆行驶里程，当路径距离最短时配送成本最优。

根据上述描述和相关假设，以车辆行驶路程最小为目标建立配送车辆路径规划数学模型为[1]

目标函数

(1)

约束条件：

(2)

(3)

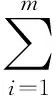
(4)

(5)

上述模型中，计量中心编号为0，各市县公司二库房为1,2,…,k；i,j为二级库房序号，s为车辆序号，gi为二级库i的智能表需求量，m为车辆总数，q为每辆车载容量，cij表示点i到点j的运输成本；xij为决策变量，表示车s是否由i驶向j，如果是xijs值为1，否则为0；yis为决策变量，表示二级库i的任务是否由车s完成，如果是yis值为1，否则为0。

目标函数(1)要求合理安排配送车辆路径，使得运输成本最小。约束条件式(2)为每辆配送车的载容量；式(3)保证了每个二级库房的配送任务仅由1辆配送车来完成，而所有的配送任务则由m辆车共同完成；式(4)和(5)限制了到达和离开某一个二级库房的配送车有且仅有一辆，并对xijs和yis的取值分别进行了限制。

3 最优路径问题求解

在算法模型构建后，应用Matlab工具对上述问题进行求解。以河北南网计量中心向衡水地区各单位配送电能表为例，实际配送路线见图2。结合配送车辆日常实际配送里程，建立各二级库房之间的等效配送距离表见表1。

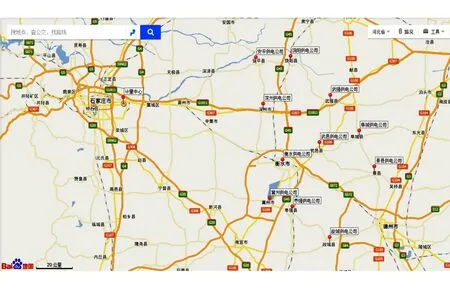
图2 省计量中心实际配送路线图

根据等效配送距离表，将地理图转换为坐标图，并设省计量中心坐标为(0,0)，二级库房数量为11个，车辆载容为1万只，各二级库房的需求总量为1.9万只，见表2。在配送分布图上进行模拟找到合理派发车辆数和最佳配送路径。

表1 二级库房等效配送距离 km

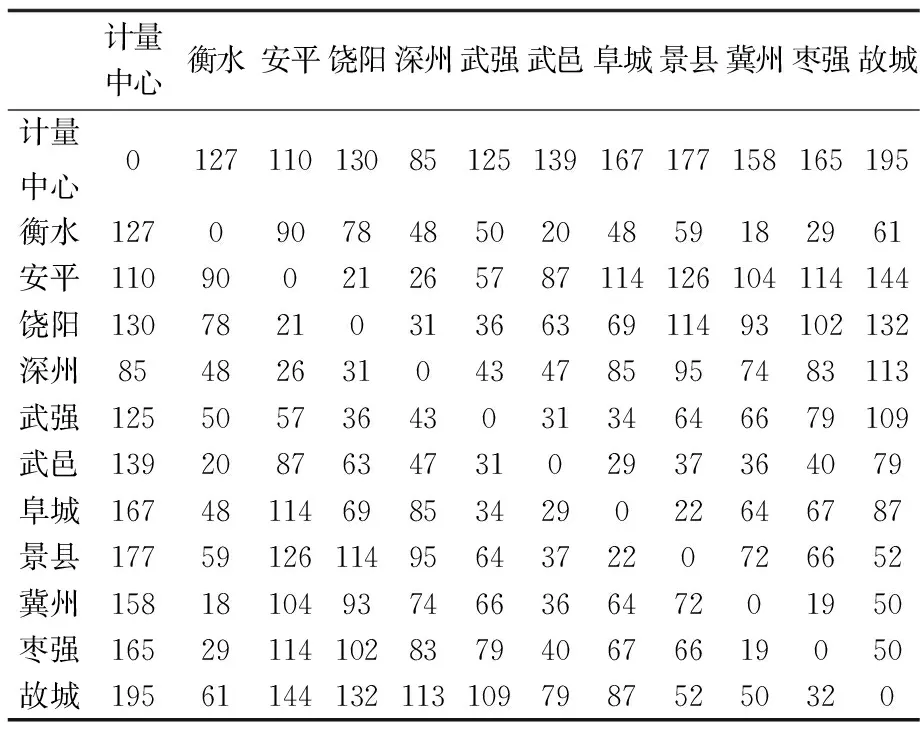
计量中心衡水安平饶阳深州武强武邑阜城景县冀州枣强故城计量中心012711013085125139167177158165195衡水127090784850204859182961安平11090021265787114126104114144饶阳130782103136636911493102132深州854826310434785957483113武强1255057364303134646679109武邑139208763473102937364079阜城1674811469853429022646787景县17759126114956437220726652冀州1581810493746636647201950枣强16529114102837940676619050故城1956114413211310979875250320

表2 各二级库房位置坐标及需求量情况

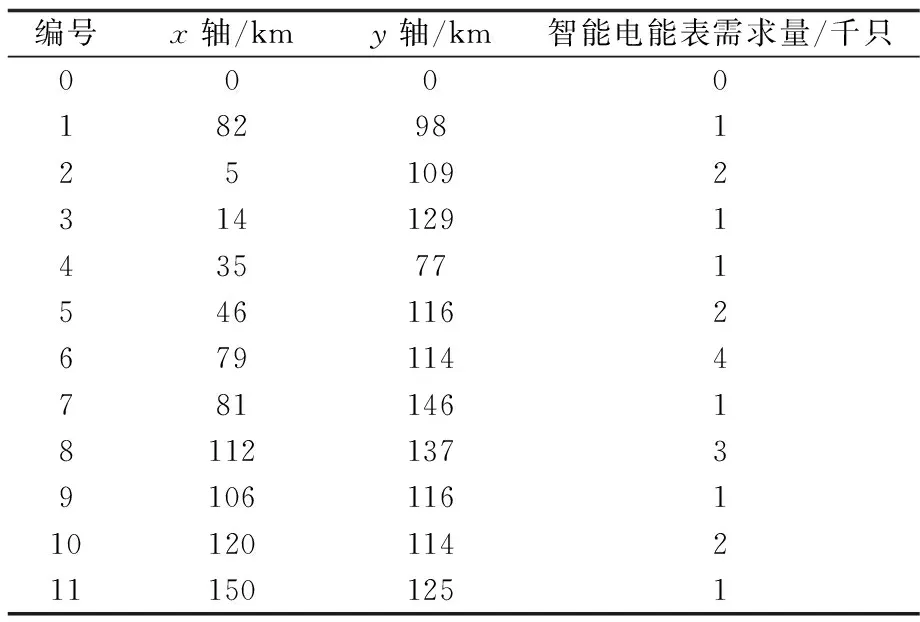
编号x轴/kmy轴/km智能电能表需求量/千只000018298125109231412914357715461162679114478114618112137391061161101201142111501251

4 路径规划优化分析

用Matlab对该优化问题进行模拟运算，设置种群规模n=500，迭代次数C=500，交叉概率Pc=0.8，变异概率Pm=0.2，经过50次蒙特卡洛模拟计算，得到的优化路径结果如图3所示。

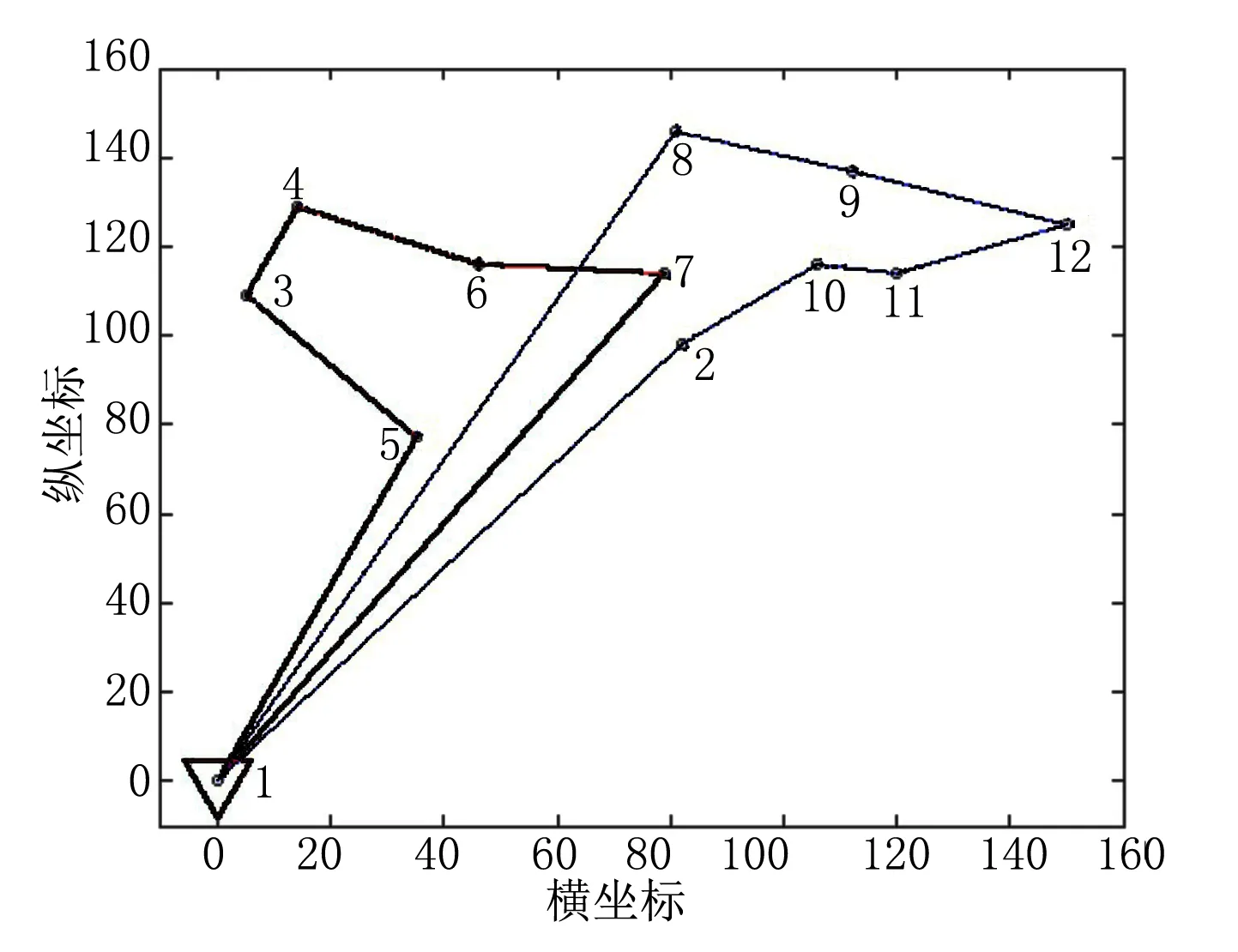
图3 智能表配送路线优化结果(12节点)

通过结果的计算可知，利用该文算法得到的优化配送路径为0→4→2→3→5→6→0→7→8→11→10→9→1→0，总里程799.644 5 km，明显优于随机法得到的结果1 025 km。图4为目标函数在约束条件下的迭代优化过程，可以看出，最优适应值在约100次迭代后即趋于收敛，表明了该算法的有效性。

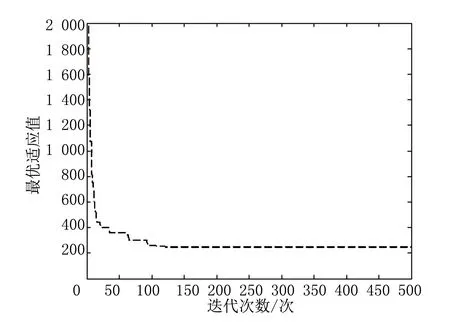
图4 适应值遗传优化过程

为了进一步验证算法性能，将二级库房数目增加至17个，按照石家庄周边分布，调整车辆容载等限制条件，重新进行试验，结果如图5所示。

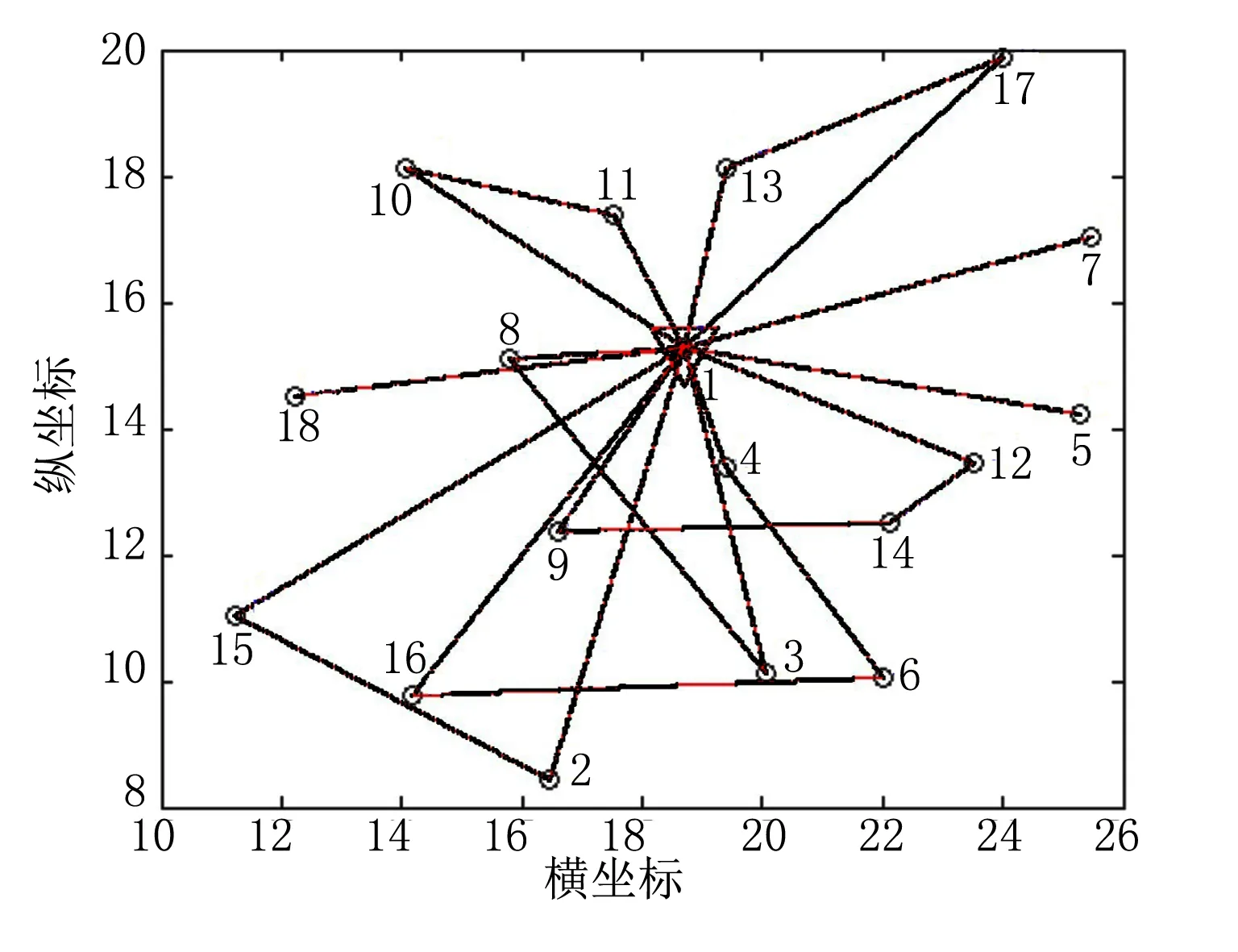
图5 智能表配送路线优化结果(18节点)

结果表明，该算法在多节点中心分布情况下仍能良好工作，将取得的结果与电能表配送日志系统进行比对，结果表明算法能够较为正确地反映配送方案的优化趋势。

5 结束语

从计量中心向n个二级库房配送会有n!个可选的路径方案，考虑到所有路径均双向可逆，文中11!个方案中每个方案都存在另一个与之重复的方案，因此实际可行解的数量为0.5×11！=19 958 400个，但是使用遗传算法可以方便地从中寻找到最优路线方案，当库房个数继续增加时，所需要的仅仅是改变编码的长度而已，设计难度基本不变，具有很好的可推广性。

根据实际运行情况统计和测算，自2015年8月正式推广应用以来，在未增加车辆和配送费用的情况下，月度平均配送效率提升18%，百km配送成本降低11%，仅2015年一年节约配送费用42.3万元，具有非常好的经济性和可推广性，建议进一步优化算法和程序，开发出适合智能表配送需求的路径自动优化系统，进一步推广应用。

[1] 李 军, 郭耀煌. 物流配送车辆优化调度理论与方法[M]. 北京: 中国物资出版社, 2001.

[2] 蒋琦玮, 陈治亚. 物流配送最短径路的动态规划方法研究[J]. 系统工程, 2007, 25(4): 27-29.

[3] 刘慧美, 董富贵, 贾朝辉. 基于遗传算法的智能电能表配送车辆优化调度[J]. 华北电力技术, 2012, 11(8): 21-25.

[4] S.Salhi, G.Nagy. Heuristic algorithms for single and multiple depot vehicle routing problems with pickups and deliveries[J]. European Journal of Operational Research, 2005, 162(1): 126-141.

[5] Z Fu, R.Eglese, L Li. A new tabu search heuristic for the open vehicle routing problem[J]. Journal of the Operational Research Society, 2005, 56(3): 267-274.

[6] 钟石泉, 杜 纲. 基于核心路径禁忌算法的开放式车辆路径问题研究[J]. 计算机集成制造系统, 2007, 13(4): 827-832.

[7] 孙小年, 陈幼林, 杨东援. 装卸一体化车辆路径问题的遗传算法研究[J]. 系统工程理论与实践, 2007, 27(2): 149-152.

本文责任编辑：王洪娟

Research and Application on Distribution Routing Optimization for Intelligent Electric Meter Based on Genetic Algorithm

Tian Guang1,Luo Peng2,Liu Penghui1,Li Tiecheng2

(1.State Grid Hebei Electric Power Company,Shijiazhuang 050021,China;2.State Grid Hebei Electric Power Research Institute,Shijiazhuang 050021,China)

To meet the demand of super large scale intelligent electric meter distribution of provincial metering center,a novel optimization selection method for intelligent electric meter distribution routing is proposed,which is based on genetic algorithm.With the application in subordinate warehouse path planning for southern Hebei network,under the restrained conditions for vehicle capacity, electric meter requirement and maximum mileage,mathematical model of distribution routing is constructed,then the global optimization of distribution path by minimizing the total cost,which providing a scientific basis for the establishment of economical and efficient distribution scheme.The simulation results verifies the efficiency of this method.

intelligent electric meter;distribution;genetic algorithm;routing optimization

2017-01-12

田 广(1983-)，男，高级工程师，主要从事督察督办管理工作。

TM763

A

1001-9898(2017)03-0007-03