基于IHB法分裂导线次档距振荡的极限环特性
2017-07-01于洋洋郭虎伦曹树谦陈予恕
于洋洋, 郭虎伦, 曹树谦, 刘 彬, 陈予恕,5
(1.天津大学力学系 天津,300072) (2.天津大学仁爱学院 天津,301636)(3.天津市非线性动力学与混沌控制重点实验室 天津,300072)(4.中国电力科学研究院 北京,100192) (5.哈尔滨工业大学航天学院 哈尔滨,150001)
基于IHB法分裂导线次档距振荡的极限环特性
于洋洋1,2,3, 郭虎伦1,3, 曹树谦1,3, 刘 彬4, 陈予恕1,3,5
(1.天津大学力学系 天津,300072) (2.天津大学仁爱学院 天津,301636)(3.天津市非线性动力学与混沌控制重点实验室 天津,300072)(4.中国电力科学研究院 北京,100192) (5.哈尔滨工业大学航天学院 哈尔滨,150001)
分裂导线中的背风子导线在尾流激振作用下会出现大幅的次档距振荡,是威胁高压输电线路安全运行的重要故障之一。针对此问题,首先,给出了背风子导线在尾流激振下,含气动非线性的两自由度次档距振荡动力学模型方程;其次,采用增量谐波平衡法推导了求解次档距振荡高阶极限环响应的方程,得到了次档距振荡极限环响应的前三次谐波响应,结果表明,导线次档距振荡只存在于一个风速区间范围内,随谐波次数的增加,高次谐波的影响明显减弱,其中一次谐波能够较好地吻合Runge-Kutta数值计算结果;最后,分析了档距和背风子导线的初始位置对次档距振荡的影响,为避免或抑制次档距振荡的发生提供技术支持。
分裂导线;次挡距振荡;极限环;增量谐波平衡法
引 言
微风振动、覆冰舞动和次档距振荡是危害输电导线安全运行的3种重要故障。次档距振荡只存在于分裂导线中,是一种由迎风侧子导线的尾流诱发背风侧子导线振动的现象。次档距振荡的振动频率约为1~3Hz,振幅为导线直径的3~20倍,会造成子导线间的相互碰撞和鞭击、磨损导线,严重的将导致导线疲劳断股[1]。当前,随着长距离、大跨度、多分裂高压输电技术的广泛应用,分裂导线中存在的次档距振荡的危害性也愈发凸显。因此对分裂导线次档距振荡动力学特性的深入研究有助于次档距振荡抑制技术的开发,避免次档距振荡的发生。
当前针对次档距振荡动力学特性的研究最直接的方法是实验研究,此外还有数值方法、解析方法和半数值半解析的方法。背风子导线受尾流激振时的气动升力和气动阻力的模拟是研究次档距振荡的基础,实验研究必不可少。Bokaian[2]通过实验测得背风子导线在尾流激振作用下的气动升力和气动阻力,并用幂级数的形式拟合出气动升力和气动阻力的表达式,其拟合结果与实验非常相近。Wardlaw[3]用风洞实验以分裂导线的节段弹性支撑模型研究其次档距振荡的稳定性条件,并得到较好的平均气动力结果。但实验研究的缺点是需要大量的物力,尤其风洞实验耗费巨大。随着计算技术的发展,尤其是商用软件的成熟,数值方法在次档距振荡中得到越来越多的应用。Lilien等[4]用有限元方法研究了两分裂三档距系统的次档距振荡,采用模态分析的方法分析了子导线的间距、质量、频率比等参数对分裂导线次档距振荡的影响。陈元坤[1]利用计算流体动力学(computational fluid dynamics,简称CFD)计算仿真分裂导线的气动特性,得到分裂导线的平均气动力系数曲线。解析方法计算简便,一度成为学者们关注的焦点。文献[5-7]采用准定常线性颤振理论研究了次档距振荡系统的振动失稳边界。Rawlins[8]采用传递矩阵法研究导线的振动特性,并结合波传递理论预测了分裂导线发生次档距振荡时的振动响应。准定常线性颤振理论、稳定性理论和传递矩阵法都是研究的次档距振荡线性模型。文献[9-10]在准定常理论研究的基础上,采用中心流行定理和正规形理论降维,研究了背风子导线非线性系统的次档距振荡。文献[11-12]采用平均法研究了背风子导线两自由度非线性系统的解析解,并分别与数值积分结果和其他文献的实验结果进行了对比,结果吻合良好。但是解析方法在求解高维非线性系统或者非线性项较多的多维系统时存在很大的求解困难,甚至无法求解。半数值半解析的方法结合了数值法和解析法的优点,能够较好地解决这一问题。增量谐波平衡法(incremental harmonic balance method,简称IHB)是一种发展较为成熟、应用较为广泛的半数值半解析的方法。唐南[13]将IHB应用于求解多自由度Van der pol自治系统,为解决多自由度系统的自激振动提供了很好的范例。晏致涛等[14]将IHB应用于覆冰输电线舞动——非线性自激振动系统的极限环求解,其结果与数值积分结果吻合良好。次档距振荡系统中存在复杂的非线性因素,采用IHB法能够很好地分析分裂导线的次档距振荡特性,既拓宽了IHB法的应用范围,又为强非线性的次档距振荡分析提供了一条新的途径。IHB法在研究强非线性的振动分析中合理可靠,且有足够的精度。
笔者考虑背风子导线气动载荷中的非线性因素,建立背风子导线尾流激振下的两自由度动力学方程,利用增量谐波平衡法研究了两分裂导线次档距振荡系统,得到次档距振荡系统随风速变化的曲线及两个失稳风速之间的极限环响应,并用Runge-Kutta数值结果验证了IHB的结果,最后分析了结构参数对次档距振荡极限环响应的影响。
1 分裂导线次档距振荡建模
如图1所示,背风子导线假定为一长度为l、直径为d、质量为m的刚性圆柱体,圆柱体被认为在迎风子导线的尾流中,圆柱体被弹簧和阻尼器支撑,数学模型考虑为背风子导线的平面运动。设背风子导线没有振动时的位置为(x0,y0),振动后为(x0+x,y0+y)。

图1 两分裂导线次档距振荡Fig.1 Subspan oscillation of two bundled conductors
根据图1背风子导线受力建立动力学方程
(1)
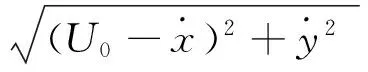
笔者采用Oliveira等[11]给出的升力和阻力的表达式
(2)
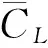
用背风侧导线位置坐标的幂级数拟合实测气动力曲线,可得CL和CD的表达式
(3)
其中:X0=x0/d;Y0=y0/d;X=x/d;Y=y/d。
其他系数分别为:c0=1.2,A01=-1.78,A11=0.127,A21=-0.002 38,A02=1.944,A12=-0.115 2,A22=0.002 304,B01=B11=B12=B52=0.0,B21=0.928,B31=-0.827,B41=0.233,B51=-0.023 9,B02=0.740,B22=-0.007 12,B32=-0.105,B42=0.026 6。
按X和Y的幂级数展开,气动力可写为
(4)
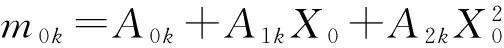
m1k=A1k+2A2kX0;m2k=A2k;
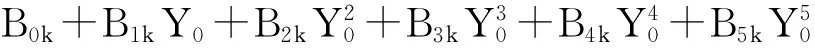

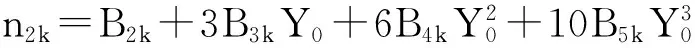
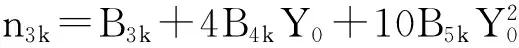
n4k=B4k+5B5kY0;n5k=B5k;k=1,2。
忽略CL和CD3次以上的非线性,可得
CL=m01n01+m11n01X+m01n11Y+
m21n01X2+m11n11XY+m01n21Y2+
m21n11X2Y+m11n21XY2+m01n31Y3
(5a)
CD=c0-m02n02-m12n02X-m02n12Y-
m22n02X2-m12n12XY-m02n22Y2-
m22n12X2Y-m12n22XY2-m02n32Y3
(5b)
升力和阻力为X和Y的函数,没有常数项,即由式(5)可得
(6)
因此背风子导线次档距振动方程为
(7)

(8)
其中:
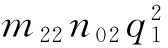
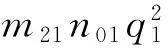
2 IHB分析
次档距振荡为自激振动,设自激振动频率为ω。令τ=ωt,则方程可无量纲化为
ω2Mq″+ωCq′+Kq+Nf(q,ωq′)=0
(9)
其中:()′和()″分别为对无量纲时间τ的一阶导数和二阶导数。
设q0和ω0为式(9)的解,其邻近状态以增量形式表示为
q=q0+Δq
(10)
ω=ω0+Δω
(11)


(12)
其中
(13)
(14)
(15)
式(13)、式(14)和式(15)中各元素的表达式为
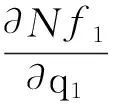
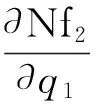
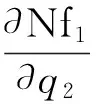
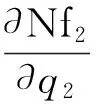
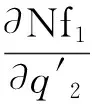
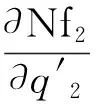
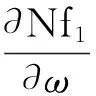
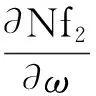
将式(10),(11),(12)代入式(9),并略去高阶小量,可得
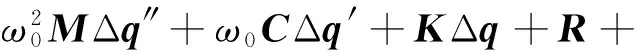
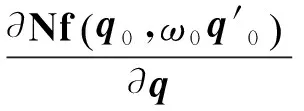

(16)
其中
(17)
为误差向量。
下面进行谐波平衡,首先设式(9)的稳态周期解为
(18)
其对应的增量可表示为
(19)
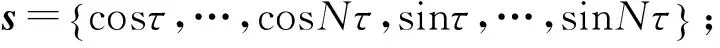
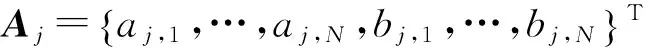
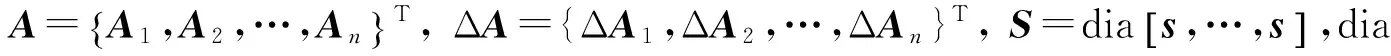
q0=SA
(20)
Δq=SΔA
(21)
将增量方程(16)左乘δ(Δq)T,并对τ在[0, 2π]上积分,可得
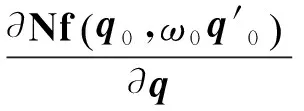
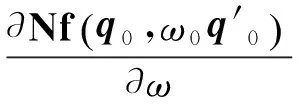
(22)
将式(20)和式(21)代入式(22)可得

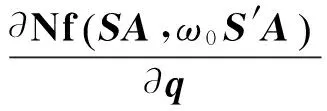
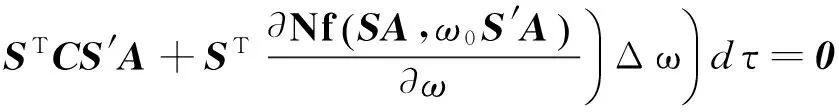
(23)
S为τ的函数,可令
(24)
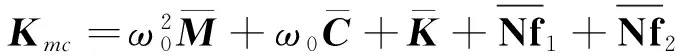
(25)
(26)
(27)
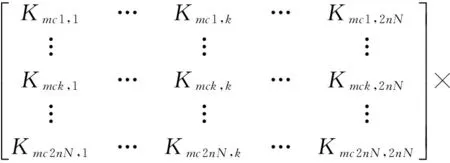
(28)
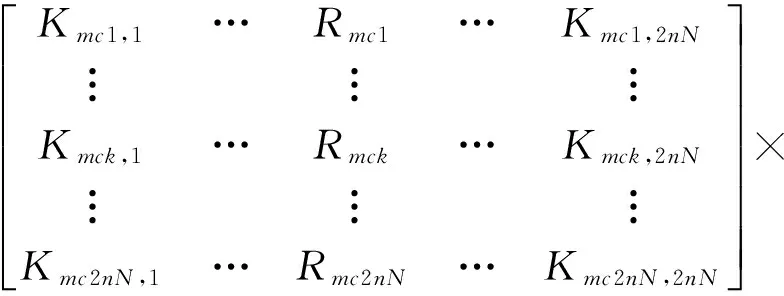
(29)

3 次档距振动特性分析
图2和图3分别为X和Y的一次谐波与数值解的幅值随风速U0的变化关系。由图可知,次档距振荡零平衡位置存在2个失稳速度U10=8.86和U20=12.62。这与文献[1]所得2个Hopf分岔点的结论和文献[11]实验结果吻合一致。当U0<
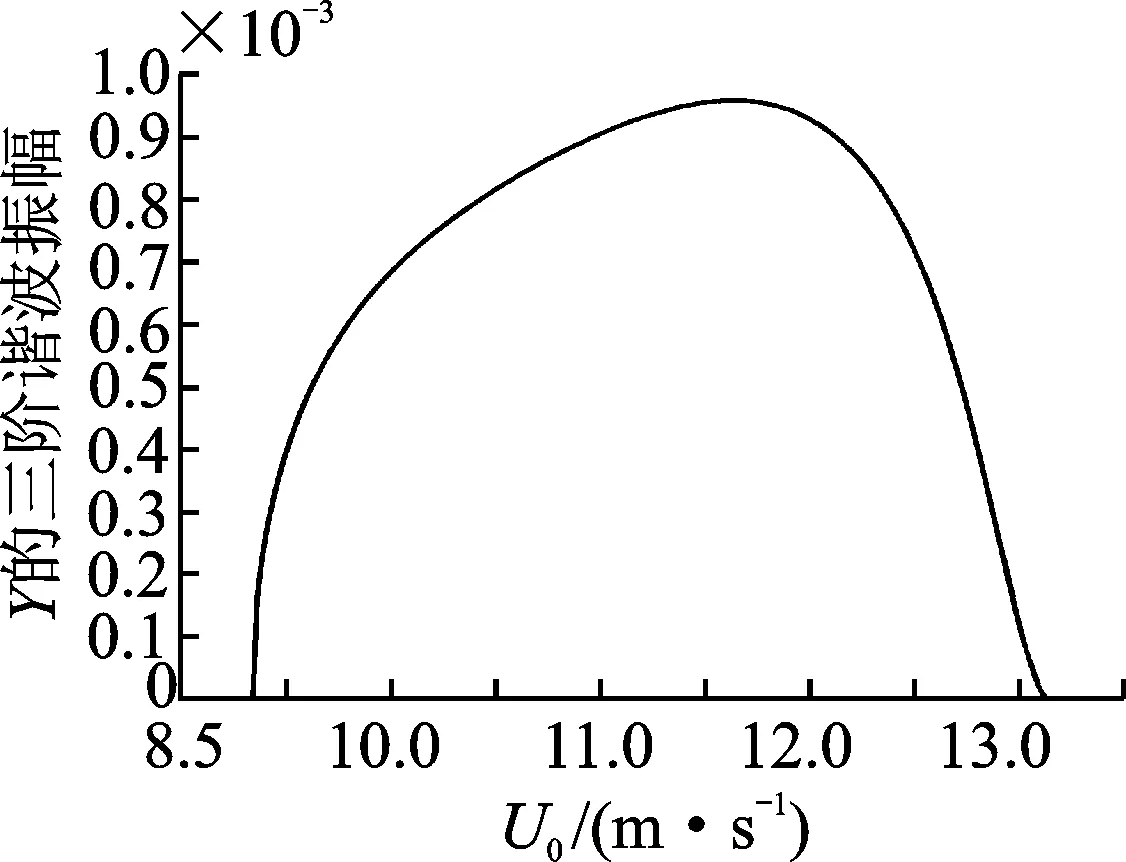
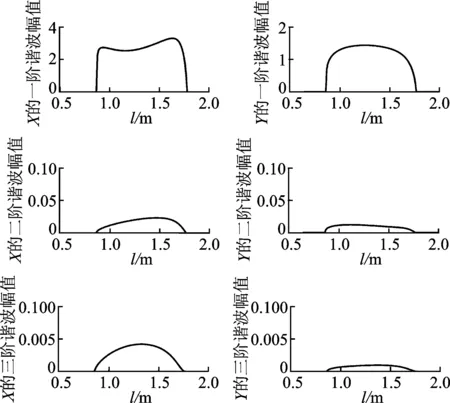
U10时,系统不存在极限环响应,系统收敛到稳定的零解上;当U10
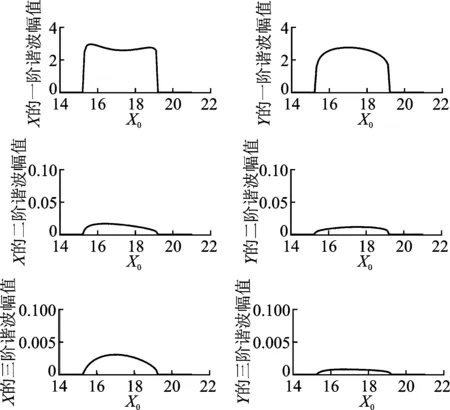
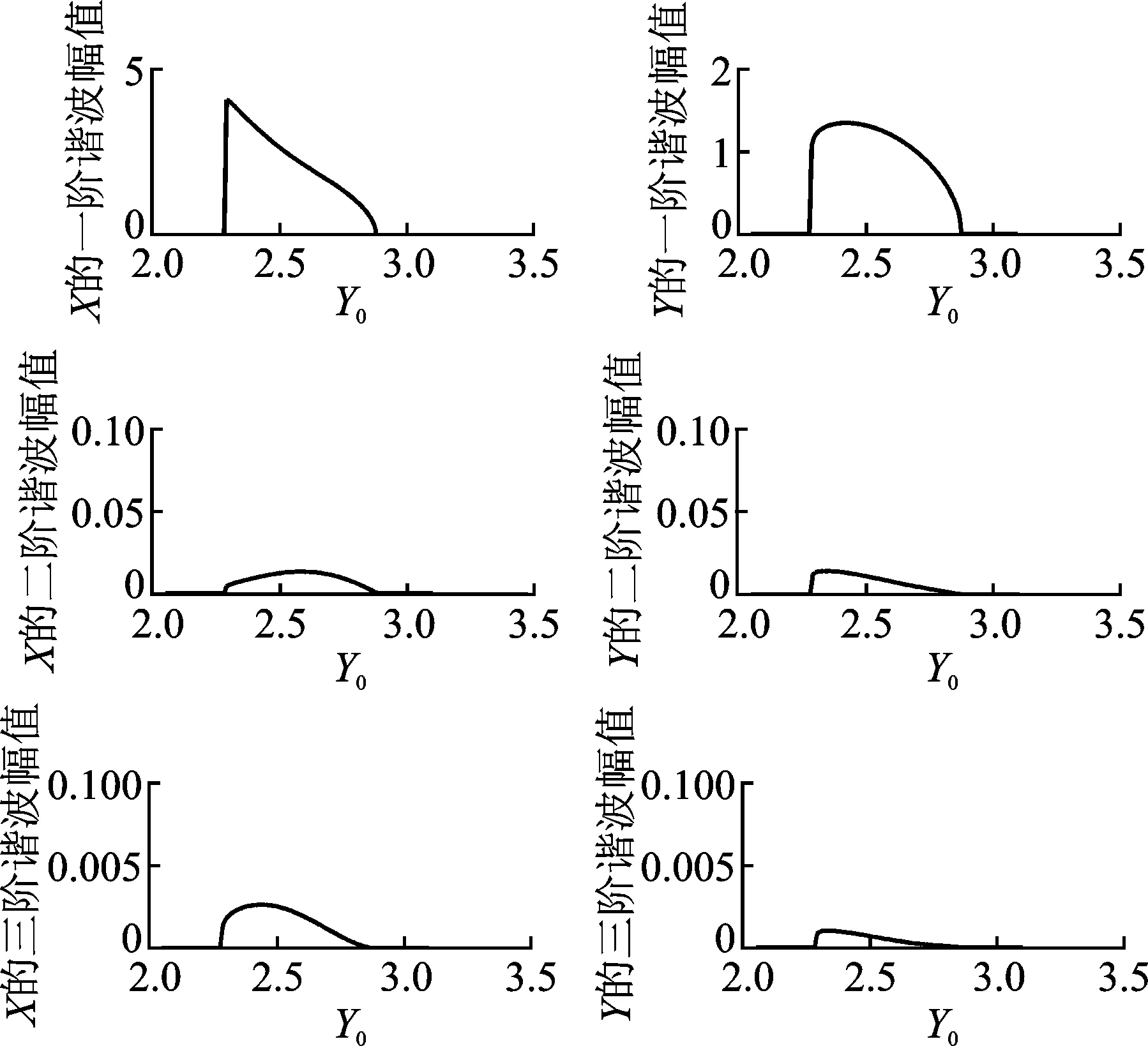
图4~图7分别为X和Y的二次和三次谐波的幅值随风速U0的变化关系。对比分析一次、二次和三次谐波的响应曲线可知,其动力学变化趋势是一致的,都是在U0< 8.86或U0>12.62时,收敛到零解;而在8.86 Fig.2 Amplitude for the first order and numerical solution ofXwith wind speedU0 图3Y的一次谐波和数值解的振幅随U0的变化 Fig.3 Amplitude for the first order and numerical solution ofYwith wind speedU0 图4X的二次谐波的振幅随U0的变化 Fig.4 Amplitude for the second order ofXwith wind speedU0 图5 Y的二次谐波的振幅随U0的变化 Fig.5 Amplitude for the second order ofYwith wind speedU0 图6X的三次谐波的振幅随U0的变化 Fig.6 Amplitude for the third order ofXwith wind speedU0 图7Y的三次谐波的振幅随U0的变化 Fig.7 Amplitude for the third order ofYwith wind speedU0 分析结构参数对次档距振荡振幅的影响,可以为防止次档距振荡的措施提供依据。取参数值U0=9.5m/s,其他参数同第3节所取。通过以上分析,取X和Y的三次谐波,可得结构参数背风子导线初始位置X0,Y0和档距l对次档距振荡的影响,如图8~图10所示。 图8 X和Y的振幅随X0的变化Fig.8 Amplitude of X and Y with X0 图9 X和Y的振幅随Y0的变化Fig.9 Amplitude of X and Y with Y0 图10 X和Y的振幅随l的变化Fig.10 Amplitude of X and Y with l 图8为X和Y的一、二、三阶谐波幅值随尾流中背风子导线初始水平距离X0的变化。其他参数不变,随X0的增加,当X0=15.2时开始存在次档距振荡极限环响应,当X0=19.2时极限环响应消失,即15.2 1) 次档距振荡系统的零平衡位置存在两个失稳速度,两个失稳速度区间之内,系统存在次档距振荡,收敛到稳定的极限环上,失稳速度区间之外,系统收敛到稳定的零解上。 2) 次档距振荡系统各阶谐波响应的失稳速度一致,且失稳区间内极限环幅值都是随风速的增大呈现出先增大后减小的趋势。 3) 各阶谐波响应随谐波阶次的增加,幅值衰减明显,二次谐波幅值远小于一次谐波,三次谐波幅值又小于二次谐波。一次谐波解能够较好地反映分裂导线的次档距振荡。 4) 当结构参数变化时,其对次档距振动振幅的影响规律为:随尾流中背风子导线初始水平距离X0、初始垂直距离Y0、档距l的增加而先增大后减小直到振动消失。因此,实际线路中应兼顾经济性与合理性的要求,将这3个参数尽可能地选择小些或者尽可能大一些,这有助于避免出现大幅的次档距振荡。 [1] 陈元坤. 分裂导线的微分振动与次档距振荡研究[D]. 武汉: 华中科技大学, 2011. [2] Bokaian A. Galloping of a circular cylinder in the wake of another[J]. Journal of Sound and Vibration, 1989, 128(1): 71-85. [3] Wardlaw R L, Cooper K R, Ko R G, et al. Wind tunnel and analytical investigations into the aeroelastic behaviour of bundled conductors [J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(2): 642-654. [4] Lilien J L, Snegovski D. Wake-induced vibration in power transmission line parametric study [C]∥Flow Induced Vibration. Paris:de Langre & Axisa,2004:6-9. [5] Simpson A. Wake induced flutter of circular cylinders: aeronautical aspects [J]. Aeronautical Quarterly, 1971, 22(2): 101-118. [6] Cooper K R. Wind tunnel and theoretical investigations into the aerodynamic stability of smooth and stranded twin-bundled power conductors [R]. Canada:National Research Council of Candat, 1973. [7] Price S J. Wake induced flutter of power transmission conductors [J]. Journal of Sound and Vibration. 1975, 38(1): 125-147. [8] Rawlins C B. Fundamental concepts in the analysis of wake induced oscillation of bundled conductors[J]. IEEE Transactions on Power Apparatus and Systems, 1976, 95(4): 1377-1393. [9] Kern G, Maitz A. Self-excited wind-induced vibrations and limit cycles in bundled conductors[J]. Meccanica, 1998,33:243-253. [10]Kern G, Maitz A. Normal form transformation and an application to a flutter-type of vibration[J]. International Journal of Non-Linear Mechanics, 1998, 33(5): 741-751. [11]Oliveira A R E, Mansour W M. Nonliner analysis of wake-induced oscillations[J]. IEEE Transactions on Power Apparatus and Systems, 1985,104(3): 727-732. [12]Price S J, Maciel Y. Solution of the nonlinear equations for wake-induced flutter via the Krylov and Bogoliubov method of averaging [J]. Journal of Fluids and Structures,1990, 4(5): 519-540. [13]唐南. 应用于范德波方程的增量谐波平衡法 [J]. 中山大学研究生学刊:自然科学版, 1995, 16(2): 43-50. Tang Nan. The incremental harmonic balance method applied to Van der pol equations [J]. Natural Science Journal of the Graduates, Sun Yat-Sen Uniersity:Natural Science Edition, 1995, 16(2): 43-50. (in Chinese) [14]晏致涛, 张海峰, 李正良. 基于增量谐波平衡法的覆冰输电线舞动分析[J]. 振动工程学报, 2012, 25(2): 161-166. Yan Zhitao, Zhang Haifeng, Li Zhengliang. Galloping analysis of iced transmission lines based on incremental harmonic balance method [J]. Journal of Vibration Engineering, 2012, 25(2): 161-166. (in Chinese) 10.16450/j.cnki.issn.1004-6801.2017.03.028 国家自然科学基金资助项目(11302145); 高等学校博士学科点专项科研基金资助项目(20130032120035) 2016-02-01; 2016-04-18 TH133.3 于洋洋,男,1989年2月生,硕士生。主要研究方向为输电导线次档距振荡。曾发表《两分裂导线次档距振荡Hopf分岔研究》(《机械科学与技术》2016年第35卷第8期)等论文。 E-mail: yangyang80233@126.com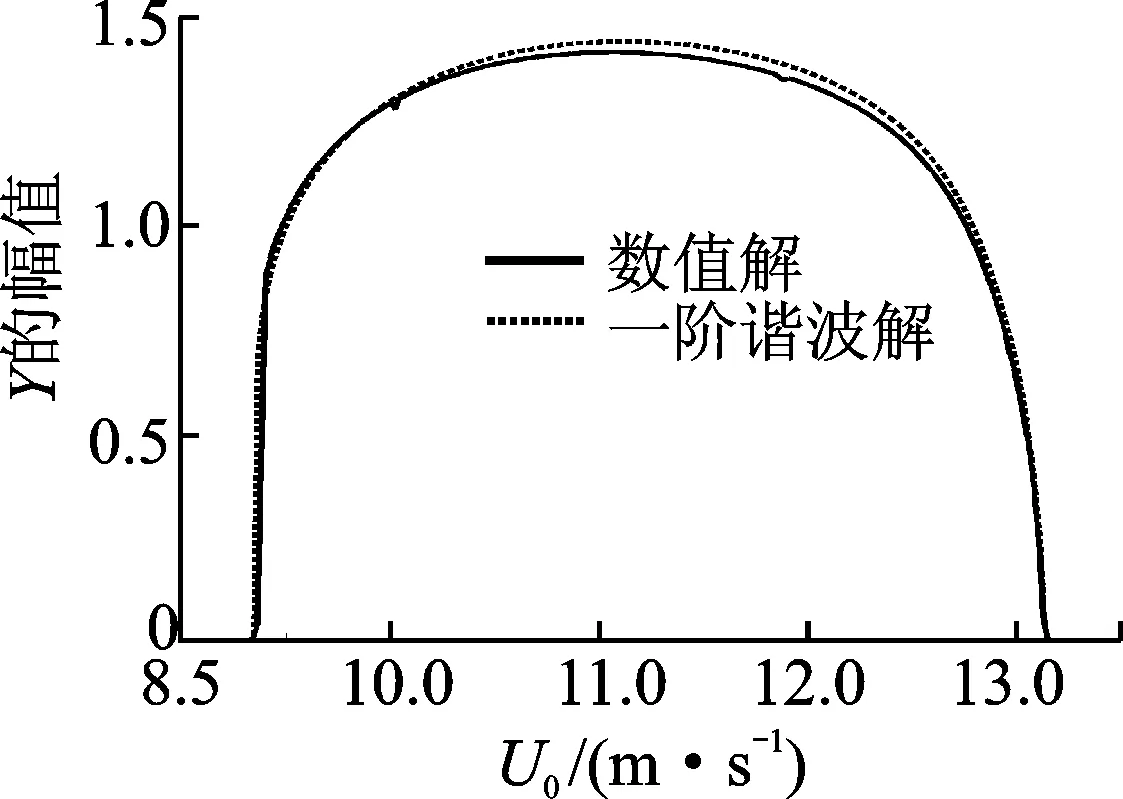



4 次档距振动结构参数分析
5 结 论

