优化支持向量机及其在智能故障诊断中的应用

2017-07-01王保建张小丽傅杨奥骁陈雪峰

振动、测试与诊断 2017年3期

关键词：齿轮轴承故障诊断

王保建，张小丽，傅杨奥骁，陈雪峰

(1.西安交通大学机械基础国家级实验教学示范中心西安， 710049)(2.长安大学道路施工技术与装备教育部重点实验室西安， 710064)

优化支持向量机及其在智能故障诊断中的应用

王保建1，张小丽2，傅杨奥骁1，陈雪峰1

(1.西安交通大学机械基础国家级实验教学示范中心西安， 710049)(2.长安大学道路施工技术与装备教育部重点实验室西安， 710064)

单一支持向量机在轴承齿轮故障诊断中精度较低，为了提高支持向量机在轴承齿轮故障诊断中的精度，对支持向量机的样本特征提取方法以及支持向量机参数优化的方法进行了研究。首先，通过核主成分分析方法构造支持向量机的输入样本，可以减少数据间的冗余，提取数据的高维信息；其次，通过粒子群优化算法优化支持向量机核函数参数和惩罚因子；最后，使用优化后的支持向量机模型进行故障诊断。通过实际轴承齿轮故障诊断对比实验，结果表明，所提方法相比一般的支持向量机诊断方法诊断精度大幅提高，验证了该混合智能诊断方法的有效性和优势。

支持向量机;核主成分;粒子群优化算法;故障诊断

引言

随着中国制造2025的提出，自动化、智能化成为我国制造业的发展方向。故障诊断技术已经发展到了智能故障诊断阶段，其中支持向量机(support vector machine，简称SVM)作为智能故障诊断技术领域的热点之一，以其基于统计学习理论的特点，非常适合故障诊断这种典型的小样本问题。目前，支持向量机在轴承、齿轮、电机等机械状态监测与故障诊断中得到了广泛应用，取得了良好的效果。根据文献[1-2]，将改进核函数的支持向量机智能诊断方案用于轴承的故障诊断，将局部均值分解与支持向量机相结合用于电机的故障诊断，以及将主成分分析和SVM结合的方法用于内燃机的故障诊断等都取得较好结果。文献[3-6]将神经网络和SVM的超参数优化用于离心泵的故障诊断，将基于物理模型的SVM用于滚动轴承的故障诊断，也取得了较好的效果。但是，目前标准的支持向量机算法通常对样本的分布假设过于理想，样本构造复杂，样本间数据存在冗余、无法提取数据间高维信息及预测速度慢、预测精度低的问题，在处理工程实际问题时容易出现问题。SVM 的性能取决于训练样本数据的质量和SVM核函数参数g和惩罚因子C的选择，因此，笔者对支持向量机的样本特征提取方法以及支持向量机参数优化的方法进行了研究。

1 SVM基本理论介绍

SVM是一种针对小样本和少样本情况下的机器学习的新方法。支持向量机不同于传统的基于经验风险最小化原则的学习方法，它是基于结构风险最小化的原则，在解决小样本、非线性及高维问题时表现出很多独特的优势[7-8]。

支持向量机的基础是寻找在线性可分条件下的最优分类超平面。首先给定一个样本集

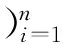
其中：xi为数据；yi为数据所属的类别。

若超平面方程wx+b=0达到了最优分类平面的标准(即在分类间隔最大的情况下将样本正确地分开)，则求解最优分类平面的问题可以转换为下述目标函数和约束条件

(1)

其中：w为权重向量；b为偏置向量。

在许多情况下，一些样本往往不能被正确地分类，为了确保分类的准确性，这里引入了松弛因子ξi≥0,i=1,2,…,n,则优化问题可以表示为

(2)

其中：C为惩罚因子。

由于算法复杂程度与分类精度之间的矛盾，通过调节惩罚因子的大小来实现折中。式(2)则变成了一个二次规划问题，通过求拉格朗日函数的鞍点得到问题的最优解。

由最优化条件(karush-kuhn-tucker,简称KKT)定理得知最初的求解最优超平面的问题被转换为求解二次优化问题

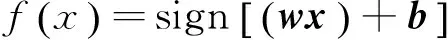
至于非线性条件下的分类问题，支持向量机的基本思想是通过核函数实现从低维向高维的映射，然后在高维特征空间中使用支持向量机进行线性分类，其具体是通过核函数来实现。现在常用的核函数包括线性核函数、高斯径向基核函数、多项式核函数及指数径向核函数等，使用不同的核函数所产生的支持向量机会得到不同的分类和预测结果。

2 智能故障诊断方法

在轴承与齿轮的故障诊断中，最常用的方法是使用各种现代信号处理方法去提取被检测信号中的故障特征频率部分。通常情况下，轴承、齿轮的故障特征频率可以通过各种一般公式直接求得；但是也有一些情况下，其故障特征频率不容易求得，或者即使求得了故障特征频率，在故障早期及噪声大的情况下也很难准确分析出特征频率。智能诊断方法不求特征频率，而是从信号的指标上进行自学习及分类。笔者采用的基于核主成分及粒子群参数优化的支持向量机智能故障诊断方法是针对设备振动信号的诊断方法，首先，采集设备振动信号；然后，采用信号的时域指标直接构造故障样本，故障样本采用核主成分进行降维及减少冗余处理，处理后的样本用于SVM训练样本，支持向量机的惩罚因子C和核函数参数g采用粒子群算法进行优化；最后，使用优化SVM对测试样本进行分类诊断。具体的方法流程图见图1。

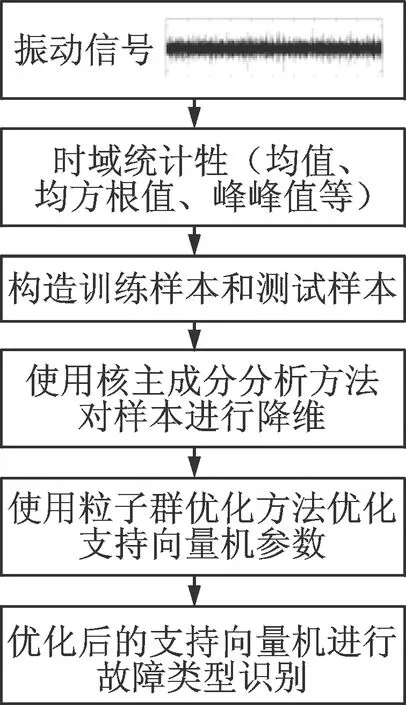
图1 方法流程图Fig.1 Method flow chart

2.1 样本构造

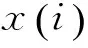
表1 几种时域统计特征

2.2 基于核主成分分析的样本处理方法

在构造时域统计特征训练样本时，时域变量(如均方根、峭度等)之间存在相关的关系，信息之间存在冗余，直接构造难免使得训练样本复杂化，进而影响分类精度。运用核主成分分析(kernel principal component analysis ，简称KPCA)方法提取这些统计特征样本的有效信息，去除冗余信息，同时减小数据的维数，可以减小计算量，加快分类速度[9-10]。

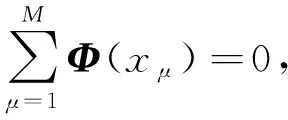
(4)

在特征空间中使用主成分分析方法，即求解方程Cν=λν中的特征值λ和特征向量ν，即有

(5)

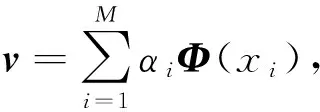
(6)

其中：v=1,2,…,M。

定义M×M的矩阵K

则式(6)可以简化为MλKα=K2α，通过对上式的求解，即可以得到所要求的特征值λ和特征向量ν。

支持向量机的惩罚因子C和核函数g的选择对预测分类精度影响很大，采用粒子群优化方法优化支持向量机参数C和g[11-13]。粒子群优化算法(particle swarm optimization algorithm，简称PSO)基本理论如下。

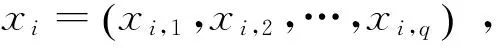
1) 自身搜索到的历史最优值

2) 全部粒子搜索到的最优值

之后每个粒子则会按照式(7)来更新自己所处的位置和此时的速度

(7)

其中：ω为惯性权重，是粒子保持自己之前的速度的权重系数；c1为粒子根据自身经验寻找最优值的权重系数，一般取2；c2为粒子根据群体经验寻找最优值的权重系数，一般也取为2；ξ,η为区间[0，1]之间均匀分布的随机数；r为约束因子，通常取1。

依据公式(3)引入产业创新速度的2次项估计其非线性效应，经检验采用固定效应模型，结果见表1。结果显示，所有变量均通过了统计检验，模型拟合优度为0.993。其中，产业创新速度二次项的弹性系数为－0.145，说明产业创新速度与创新效益之间呈倒U型曲线关系，产业创新速度弹性最高点取自然对数后为4.586，转换成产业创新速度为98.10%。即当产业创新速度小于98.10%时，产业创新速度越高，其弹性系数越大;当产业创新速度大于98.10%时，产业创新速度越大，其弹性系数越小。

粒子群优化算法流程见图2。

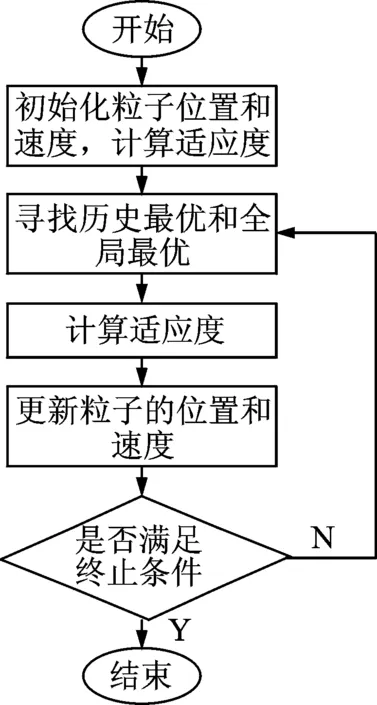
图2 粒子群优化算法流程图Fig.2 Flow chart of particle swarm optimization algorithm

3 轴承齿轮系统故障诊断实验

笔者所提方法经过仿真数据实验，结果表明本方法比直接用SVM诊断精度大为提高。为了进一步验证所提方法有效性，在故障模拟实验台上进行了轴承和齿轮的故障模拟实验。实验系统结构如图3所示，实物如图4所示。该系统主要包括SQI(MFS-PK4)故障模拟实验台(转子由2个轴承支撑，电机用过联轴器带动转子旋转，转子通过皮带轮带动齿轮箱运动)、PCB加速度传感器及东华数据采集系统。通过更换转子系统的支撑轴承来模拟不同故障的轴承，包括正常轴承、内圈故障、外圈故障、滚动体故障及混合故障5种情况；通过更换齿轮箱的齿轮来模拟不同齿轮故障，包括正常齿轮、齿轮缺齿、齿轮断齿及齿轮均匀磨损4种情况，其中齿轮均匀磨损有一个专用的齿轮箱来模拟。一个加速度传感器置于右端轴承座上方(按照径向方向)采集轴承振动信号，另一个置于齿轮箱上方采集齿轮振动信号，采样频率为12.8kHz。实验用故障轴承及故障齿轮如图5所示。

使用所采集振动信号的前一半样本作为训练样本集，后一半样本作为测试样本集，得到了70个训练集样本和70个测试集样本。由于径向基核函数(rbf)具有很好的学习能力，所以本研究中SVM的核函数均采用径向基核函数。

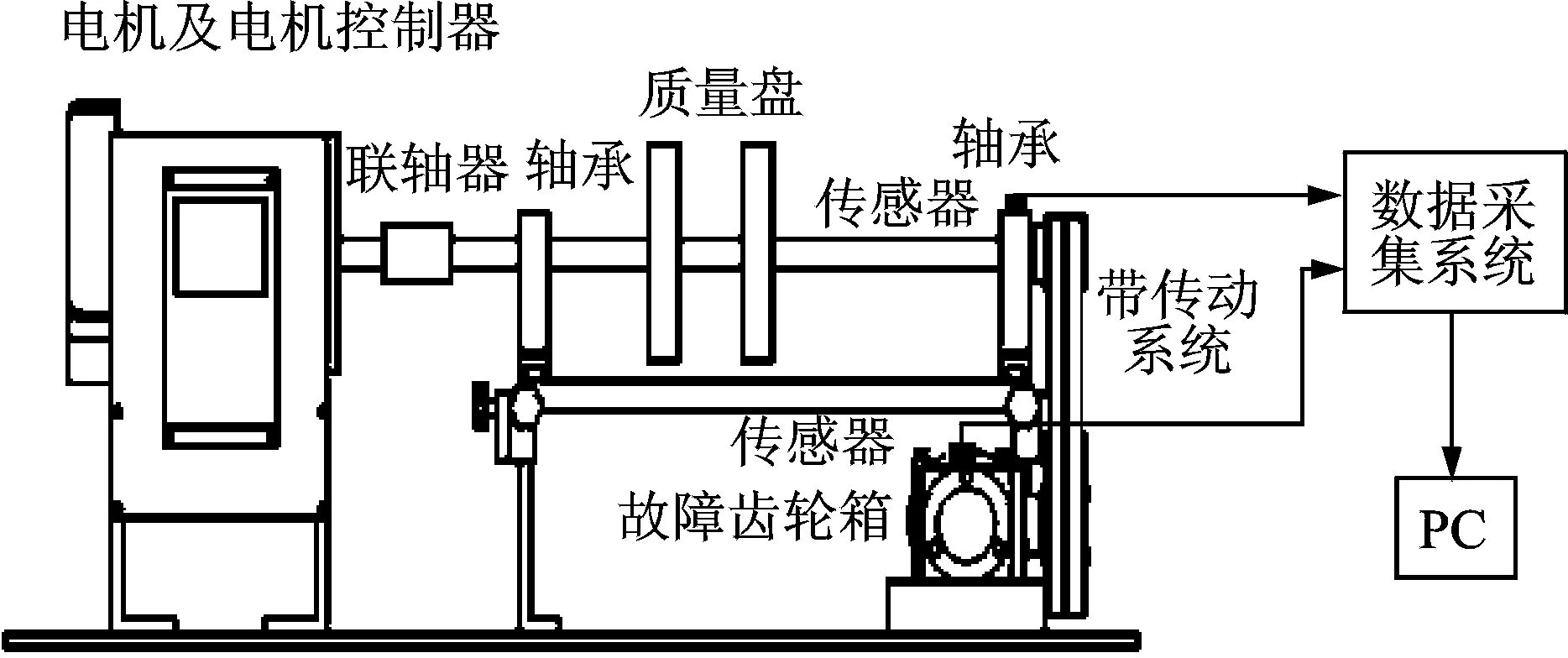
图3 实验系统结构示意图Fig.3 Schematic diagram of experimental system structure

图4 实验系统实物图Fig.4 Physical picture of experimental system

图5 故障轴承及故障齿轮Fig.5 Fault bearing and fault gear

为了验证所提方法的有效性，笔者采用了不同方法对比的研究思路，具体如下。

对比测试1：使用16个时域指标构造样本，直接使用不经过优化的支持向量机进行分类，参数为C=3，ker=rbf，g=2，实验分类精度Acc=87.14%(61/70)，如图6所示。其中：圈表示测试样本的标签；星号表示支持向量机判别的对应样本的标签。如果星号与圈重合，则判别正确；否则判别错误。

图6 轴承对比测试1的实验结果Fig.6 Experimental results of bearing contrast test 1

对比测试2：使用16个时域指标构造样本，使用经过粒子群优化的支持向量机进行分类，优化结果为C=4.487，ker=rbf，g=0.514，实验结果为Acc=92.86%(65/70)。

对比测试3：使用主成分分析方法重构样本，再使用粒子群优化参数后的支持向量机进行分类，参数优化后为C=56.45，ker=rbf，g=5.13，实验结果为Acc=97.14%(68/70)，如图7所示。

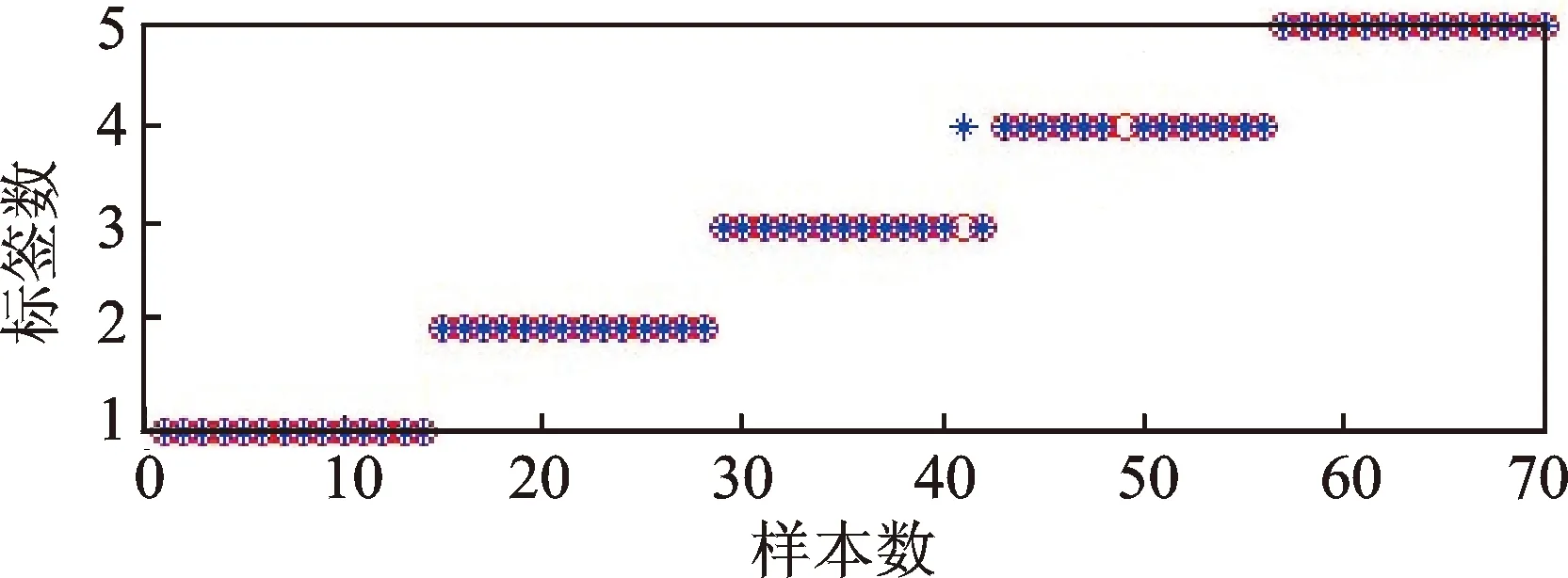
图7 轴承对比测试3的实验结果Fig.7 Experimental results of bearing contrast test 3

对比测试4：使用16个时域统计特征作为核主成分分析的输入矩阵，通过核主成分分析方法，选取主成分矩阵前l列累计贡献率达到95%的主成分作为支持向量机的输入样本，在轴承实验中前2列的累计贡献率达到99%，在齿轮试验中前4列的累计贡献率达到99%。轴承和齿轮的主成分累计贡献率如图8所示。

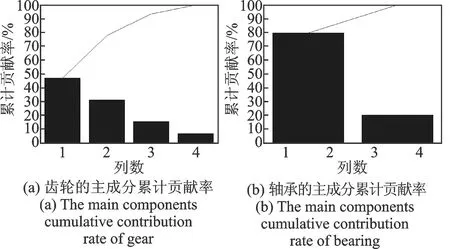
图8 轴承和齿数的主成分累计贡献率Fig.8 The main components cumulative contribution rate of bearing and gear

使用粒子群优化参数后的支持向量机进行分类，参数优化后为：C=33.2，ker=rbf，g=61.4，实验结果为Acc=100%(70/70)，如图9所示。从图中可以看出，所有的样本均被正确分类。

图9 轴承对比测试4的实验结果Fig.9 Experimental results of bearing contrast test 4

轴承故障诊断的4次对比测试结果汇总于表2，齿轮故障诊断的4次对比测试结果见表3。

表2 轴承对比实验结果

SVM为支持向量机;PSO为粒子群优化算法;PCA为主成分分析;KPCA为核主成分分析

表3 齿轮对比实验结果

从轴承和齿轮单独样本的故障诊断结果来看，粒子群算法优化支持向量机(PSO-SVM)的参数后，分类精度提高了。在此基础之上使用主成分分析方法构造样本(PCA-PSO-SVM)，去除了原有样本中的冗余信息，简化了样本的构造，精度进一步提高。使用核主成分分析构造样本时(KPCA-PSO-SVM)，较主成分分析而言，其能够提取样本数据之间高维的信息，进一步提高了精度。

4 结束语

采用核主成分加粒子群算法优化支持向量机参数的方法，构造了一套混合智能故障诊断系统。核主成分分析方法方便了样本矩阵的构造，减小了数据的冗余，提取了样本数据之间的高维信息，采用粒子群优化算法对支持向量机核函数参数g及惩罚因子C进行了优化，完成了机械故障模拟实验台上轴承和齿轮的故障诊断实验。通过与使用一般时域指标方法、使用主成分分析方法两种构造样本方法及SVM参数不优化和优化进行实验对比，结果表明，所提方法在轴承和齿轮两种数据样本上的诊断上精度非常高，证明了所提方法的科学性和有效性。

[1] 刘永斌,何清波,孔凡让. 基于PCA和SVM的内燃机故障诊断[J]. 振动、测试与诊断,2012,32(2):250-255.

Liu Yongbin,He Qingbo,Kong Fanrang. Fault diagnosis of internal combustion engine based on PCA and SVM[J]. Journal of Vibration,Measurement & Diagnosis,2012, 32(2):250-255.(in Chinese)

[2] 鞠华,沈长青,黄伟国. 基于支持向量回归的轴承故障定量诊断应用[J]. 振动、测试与诊断,2014,34(4):767-771.

Ju Hua,Shen Changqing,Huang Weiguo. Application of bearing fault quantify diagnosis based on support vector regression[J]. Journal of Vibration,Measurement & Diagnosis, 2014,34(4):767-771. (in Chinese)

[3] Azadeh A, Saberi M, Kazem A, et al. A flexible algorithm for fault diagnosis in a centrifugal pump with corrupted data and noise based on ANN and support vector machine with hyper-parameters optimization[J]. Applied Soft Computing, 2013, 13(3): 1478-1485.

[4] Gryllias K C, Antoniadis I A. A support vector machine approach based on physical model training for rolling element bearing fault detection in industrial environments[J]. Engineering Applications of Artificial Intelligence, 2012, 25(2): 326-344.

[5] Chen Fafa, Tang Baoping, Song Tao, et al. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization[J]. Measurement, 2014, 47: 576-590.

[6] Kuang Fangjun, Zhang Siyong, Jin Zhong, et al. A novel SVM by combining kernel principal component analysis and improved chaotic particle swarm optimization for intrusion detection[J]. Soft Computing, 2015, 19(5): 1187-1199.

[7] Shen Zhongjie. Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine[J]. Journal of Mechanical Engineering, 2013, 49 (2): 183-189.

[8] 郭明玮,赵宇宙,项俊平. 基于支持向量机的目标检测算法综述[J]. 控制与决策,2014(2):193-200.

Guo Mingwei, Zhao Yuzhou, Xiang Junping. A review of the target detection algorithm based on support vector machine[J]. Control and Decision,2014(2):193-200. (in Chinese)

[9] 彭令，牛瑞卿，赵艳南.基于核主成分分析和粒子群优化支持向量机的滑坡位移预测[J]. 武汉大学学报，2013，38(2)：148-452.

Peng Ling, Niu Ruiqing, Zhao Yannan. Landslide displacement prediction based on kernel principal component analysis and particle swarm optimization support vector machine [J]. Journal of Wuhan University,2013，38(2)：148-452. (in Chinese)

[10]李平,李学军,蒋玲莉. 基于KPCA和PSOSVM的异步电机故障诊断[J]. 振动、测试与诊断,2014,34(4):616-620.

Li Ping,Li Xuejun,Jiang Lingli. Fault diagnosis of induction motor based on KPCA and PSOSVM[J]. Journal of Vibration,Measurement & Diagnosis,2014,34(4):616-620. (in Chinese)

[11]聂立新,张天侠,赵波. 粒子群算法优化双核支持向量机及应用[J]. 振动、测试与诊断,2014,34(4):565-569.

Nie Lixin, Zhang Tianxia, Zhao Bo. Particle swarm optimization algorithm for dual core support vector machine and its application[J] . Journal of Vibration,Measurement & Diagnosis,2014,34(4):565-569. (in Chinese)

[12]谷文成,柴宝仁,滕艳平. 基于粒子群优化算法的支持向量机研究[J]. 北京理工大学学报,2014(7):705-709.

Gu Wencheng, Chai Baoren, Teng Yanping. Research on support vector machine based on particle swarm optimization algorithm[J] .Journal of Beijing Institute of Technology ,2014(7):705-709. (in Chinese)

[13]张周锁，侯照文，孙闯.应用粒计算的混合智能故障诊断技术研究[J]. 西安交通大学学报，2011，45(1)：48-53.

Zhang Zhousuo, Hou Zhaowen, Sun Chuang. Research on the technology of hybrid intelligent fault diagnosis based on granular computing[J]. Journal of Xi′an Jiaotong University，2011，45(1)：48-53.(in Chinese)