基于线性变换的测定电源电动势与内阻实验数据处理

王鹏

1引言

众所周知，图像绘制和数据分析是中学物理实验教学的重要内容。在具体的实验过程中，由于仪器设备及实验方法等主客观因素的存在，实验数据总呈现出不确定性。例如，在伏安法测定电源的电动势与内阻实验中，路端电压U和干路电流I的实验数据并不是确定的线性关系，只有在理想情况下才满足直线方程。另外，采用手工绘图和计算，不符合严格的统计理论，实验处理结果的真实性和准确性不高。

本文以“测定电源的电动势E与内阻r实验”为例，采用Ori gin软件建立散点图模型，同时进行相关性检验，拟合出最优的和最能代表试验数据的线性方程，从而准确地计算出电源的电动势与内阻。

2实验的模型与原理

“测定电源的电动势与内阻”实验常用的方法有4种：①电压表与电流表（伏安法）；②电流表与电阻箱（安阻法）；③电压表与电阻箱（伏阻法）；④电流表与电流表（安安法），实验电路如图1所示。上述实验方法，均通过线性变换，根据实验数据图像，利用斜率和截距法直观、准确地得出实验结果。

实验依据闭合电路的欧姆定律，其中U为路端电压，I为干路电流，E和r分别为待测电源的电动势和内阻。利用线性变换，得到上述物理模型对应的线性方程，以及方程的斜率k与截距b，见表1。

3基于线性变换处理实测数据

闭合开关，调节变阻器，使电表有明显示数变化，记录电流表和电压表相应的读数。

在Ori gin软件的工作表中输入实验数据，点击Plot/Scatter，软件就会自动画出如图2所示的相应数据的散点图。

从图2中可以看出，这些散点关系近似于直

线。选择1条直线来表示上述线性变量的关系，即y=kx+b。基于传统的数据处理方法，物理教师一般要求学生手工绘制这样1条直线，即尽可能多的点通过直线。但如此处理方法粗糙，实验误差较大，严格准确的做法是基于统计理伦，基于最小二乘法拟合计算出线性方程的斜率k和截距b。下面以伏安法为例，利用Ori gin求解电压U与电流I的线性回归方程的斜率和截距。

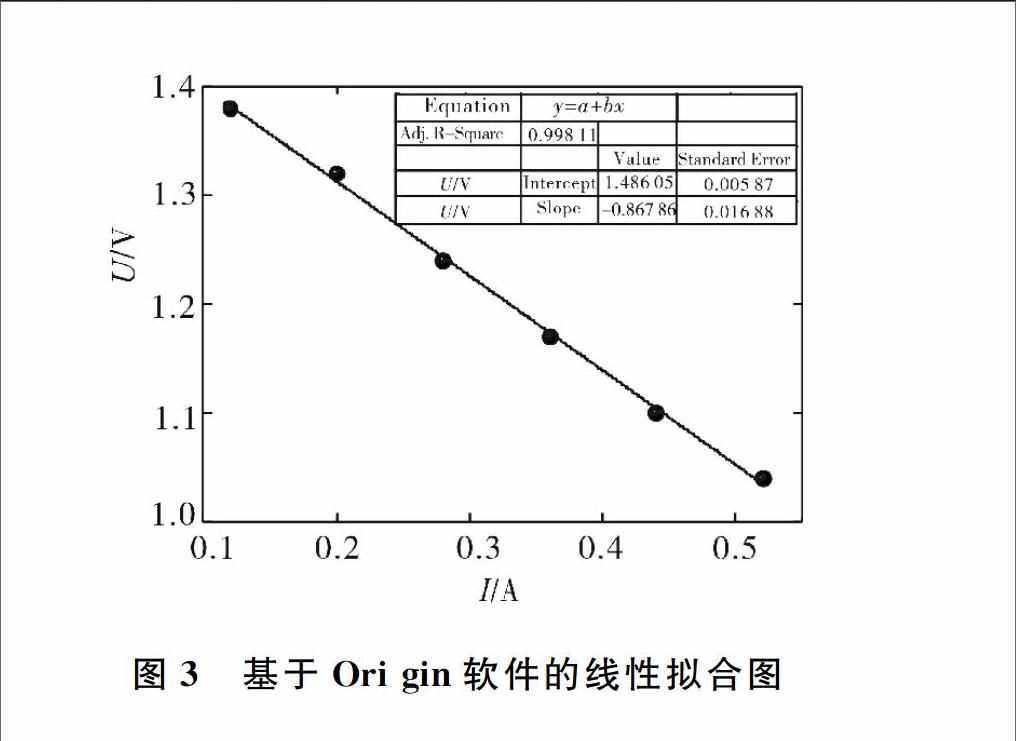
在Analysis菜单下点击“Fittin g/ Fit Linear + Open Dialo gue”，Ori gin软件自动对散点图进行线性拟合，同时给出拟合直线的斜率和截距及其誤差等相关参数，如图3所示。

如图3所示，相关系数R2=0.998 11说明公式y=kx+b中，x与y，即I与U的相互联系密切程度和拟合所得的线性方程的可靠程度较高，表明实验数据关系几乎是一条直线。线性回归直线方程为y=—0.867 86x+1.486 05，直线斜率k=-0867 86，截距b=1.486 05，而斜率和截距的物理意义分别为k=-r和b=E，可以求出r=0867 86 Ω，E=1.486 05 V。

4结论

应用Ori gin软件建立散点图模型，对测定电源的电动势与内阻实验数据进行线性变换处理，并对实验数据进行相关性检验。拟合得到符合统计规律的线性方程，从而准确地计算出电源的电动势与内阻，减小了手工绘图与计算引入的人为因素误差，极大地提高了数据处理的准确性与可靠性。