基于自适应变异差分进化算法的溶解氧浓度控制系统

汤 伟 白志雄 高 祥

(1.陕西科技大学电气与信息工程学院,陕西西安,710021；2.陕西科技大学机电工程学院,陕西西安,710021；3.陕西农产品加工技术研究院,陕西西安,710021)



·溶解氧控制系统·

基于自适应变异差分进化算法的溶解氧浓度控制系统

汤 伟1,3白志雄2,*高 祥2

(1.陕西科技大学电气与信息工程学院,陕西西安,710021；2.陕西科技大学机电工程学院,陕西西安,710021；3.陕西农产品加工技术研究院,陕西西安,710021)

溶解氧是造纸中段废水好氧处理过程中的重要参量,但溶解氧过程控制回路存在大时滞、非线性等问题,常规PID控制难以收到理想效果。本课题在分析差分进化算法的基础上,提出了一种自适应变异差分进化算法,用于PID控制器的参数优化,实现对溶解氧浓度的精准控制。MATLAB仿真结果表明，与常规PID控制和基于传统差分进化算法的PID控制相比,本算法具有响应速度快、超调量小的优点,能够收到良好的控制效果。本算法已经投入实际应用,CODCr去除率达到84.5%,BOD去除率达到93.4%,水处理系统运行良好,能够实现废水达标排放。

溶解氧；PID；差分进化算法；自适应变异

(*E-mail: 1070727987@qq.com)

制浆造纸工业中经过洗涤、筛选、漂白以及打浆过程中所排出的中段废水,一般采用厌氧加好氧的方法处理[1]。在好氧处理过程中(见图1),溶解氧(Dissolved Oxygen,DO)浓度是重要的控制变量[2]。通过对曝气池中鼓风量的控制可以实现对DO浓度的控制,但DO浓度控制系统具有时滞性、非线性、难以精确建模等特点[3],使得对DO浓度的控制难上加难,如何寻求合理控制DO浓度的控制算法及策略成为目前制浆造纸废水处理亟待解决的问题。

目前,DO的控制多采用传统的PID控制[4],由于PID控制不需要特别精确的数学模型,易于在线整定而被广泛应用。但是实际应用中PID参数的整定多采用人工经验整定的方法,其控制效果存在精度不高以及能耗过大的问题。近年来,采用智能优化算法对PID控制器参数整定已成为一大研究热点,如模糊控制、遗传算法、粒子群算法等[5-7]。本课题采用自适应变异差分进化算法优化DO控制PID参数,使系统运行中保持合适的瞬态参数,克服了传统PID控制器参数不可改变的缺点,提高了系统的鲁棒性和控制效果。

图1 好氧废水处理过程基本工艺流程图

1 DO浓度控制系统

1.1 DO控制系统组成

好氧处理过程中,曝气池中DO浓度直接影响微生物活性,因此需要向曝气池中不断鼓入氧气。根据经验,曝气生物滤池中DO浓度维持在2.0 mg/L曝气池中的生物活性最大,处理效果最佳[8]。实际的DO浓度控制是根据曝气池出口处DO浓度和设定值的差值,通过PID控制器调节风机的鼓风量来控制曝气池中的DO浓度,风机的转速由变频器进行调节。DO浓度控制系统原理见图2,由图2可知，该系统由PID控制器、变频器、风机、进出口DO检测仪、流量计等组成。

图2 曝气池溶解氧浓度控制原理

1.2 DO控制系统数学模型

首先根据物料平衡算式,质量净变化率=质量输入率-质量输出率+反应消耗率。得出DO浓度的动态模型[9]见式(1)。

(1)

式中,V为曝气池池容积；Q为空气流量；C为曝气池DO浓度；C0为鼓入空气的DO浓度；C1为曝气池出水中DO浓度；K为反应速率常数。

对式(1)进行拉普拉斯变换可得式(2)。

(2)

(3)

式(3)可近似认为是曝气过程的仿真模型,并且可以简化为一阶惯性环节串联一阶滞后环节,其传递函数一般描述为式(4)。

(4)

通过对某曝气池进行阶跃响应建模,得到如下模型参数[10]：R=1/2,T=1/2,τ=1。因为τ/T=2>0.5,因而可以看出DO浓度控制时一个大时滞过程。同时,当进水水质、曝气池的温度以及pH值发生变化时,都会对DO浓度产生影响,故DO浓度控制也具有时变非线性的特性。这就要求控制系统具有良好的鲁棒性,当被控对象的数学模型在一定范围变化时,其自适应能力及控制效果仍较好。

2 差分进化算法及改进

2.1 基本差分进化算法

(5)

(6)

(7)

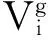
2.2 自适应变异差分进化算法

DE算法运行初期,种群多样性丰富,探索能力强,但随着演化代数的增加,群体之间的差异度减小,后期收敛速度变慢,容易陷入局部最优解。同时,DE算法的收敛速度和搜索鲁棒性之间发生冲突,难以同时得到良好的鲁棒性和快速的收敛速度。针对上述DE算法的缺点和不足,本课题主要针对变异和交叉操作进行改进,提出了自适应变异差分进化(AdaptiveMutationDifferentialEvolution,AMDE)算法。

2.2.1 基于群体相似度系数动态调整变异模式

(1)群体相似度系数的定义

群体相似度系数ε,通过定义群体中个体适应值与当前群体最优适应值的相似程度来间接衡量进化过程中种群的多样性,判断算法是否陷入停顿。ε→0,相似度高群体多样性丰富,ε→1,相似度低群体多样性差，见式(8)。

(8)

式中,fbest为种群最优适应值；fi为种群个体适应值。

(2)改进的变异操作模式

为了解决算法收敛速度和全局寻优能力之间的矛盾,本课题将两种变异模式进行结合使用,具体变异实现步骤为：

(a)引入新种群Y=[Y1,Y2,…YNP]T,其中每个个体为Yi=[yi,1,yi,2,…yi,D]。

(9)

(b)变异操作方式为：

(10)

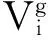
图3 群体相似度进化曲线图

2.2.2 基于变异个体优劣系数自适应交叉概率因子

(1)个体优劣系数的定义

个体优劣系数δ,通过定义种群中个体的适应值与当前种群平均适应值的比值来说明个体的优劣。以求解某函数最小值为例,δ<1表示当前个体较优,反之则个体较差。

(11)

式中，fi为当前种群中的个体适应值,favg为与当前种群平均适应值。

(2)改进的交叉操作模式

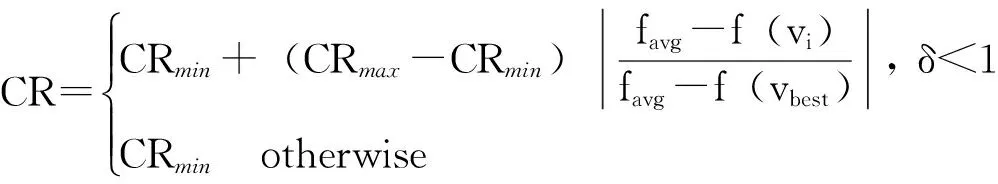
(12)

式中，favg代表当前变异矢量群体的适应度大小平均值,f(vi)表示当前变异矢量个体,f(vbest)表示当前变异矢量群体适应度最优值,CRmax和CRmin分别为CR取值的上下限。

式(12)说明,当δ<1,也就是当f(vi)小于当前变异矢量群体的平均适应值,说明此时产生的f(vi)变异矢量个体较优,实验矢量个体要以较大的概率取自变异矢量个体,那么相对应的CR值就越大。反之,δ≥1,则说明对应的变异矢量个体较差,CR取CRmin使得变异矢量对实验矢量贡献越小。图4为AMDE算法求解某函数最小化问题时基于变异个体动态交叉概率因子动态图。

图4 基于变异个体的动态交叉概率因子动态图

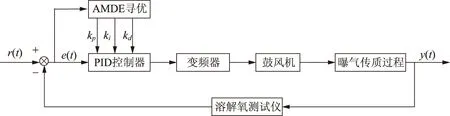
图5 基于AMDE算法的DO浓度控制系统结构

3 基于AMDE算法的DO浓度PID控制方案

3.1 DO浓度控制系统的结构

针对现有DO浓度控制系统存在的难点,本课题提出的DO浓度控制系统结构如图5所示。其中r(t)为DO浓度设定值,y(t)为DO浓度的当前值,e(t)为偏差。PID控制器由AMDE算法进行参数寻优。

3.2 基于AMDE算法的PID控制器参数优化

常规PID控制器一般形式为式(13)。

(13)

通过AMDE算法对PID参数优化,首先以待寻优的比例系数kp、积分时间常数ki和微分时间常数kd三个参数为分量构成一个三维行向量,进行浮点数编码,组成差分进化算法的个体X(kp,ki,kd)。以ZN法获得的参数为基准,按照式(14)向两边扩展作为算法的搜索空间。

(14)

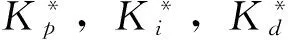
以系统的性能指标作为AMDE算法的适应度函数,目前在满足系统稳定的条件下常用的一些性能指标如下：

本课题采用常用的时间绝对偏差积分ITAE作为控制系统性能指标函数,PID参数设计的目的就是使得性能指标函数最小,由于AMDE算法具有较强的搜索能力,经过一系列寻优迭代,可以把需要优化的PID 参数放大,实现较大范围的搜索空间,摆脱了传统的PID 过于依赖经验值的缺陷。综上所述,基于AMDE算法的PID控制器参数寻优的流程如下：

(1)设定种群规模NP、变异因子F、交叉概率因子上限CRmax和下限CRmin、最大迭代次数G、PID三个参数kp,ki,kd的上下限,并随机产生初始种群。

(2)计算当前群体中个体适应值和群体相似度系数ε,得到最优个体,同时按照式(10)选择相应的变异操作模式。

(3)计算变异个体优劣系数δ,根据式(12)得到相匹配的交叉概率因子CR。按照式(6)进行交叉操作。

(4)适应度函数采用误差性能指标ITAE,按式(7)进行选择操作。

(5)如果满足最大迭代次数,则退出算法,得到最优解。否则,返回步骤(2)。

4 算法仿真

为了观察AMDE算法整定PID参数对DO浓度控制效果,在MATLAB中对本课题DO浓度控制回路方案进行了仿真研究,根据仿真得到的阶跃响应曲线来判断控制方案的优缺点,并与其他控制方案从超调量、调整时间、抑制干扰及控制系统鲁棒性等方面进行比较,体现本课题DO浓度控制方案的优越性。

当系统模型参数匹配时,根据式(4)在Simulink中搭建好仿真模型,设定AMDE算法参数,种群规模NP=50、变异因子F=0.8、交叉概率因子上限CRmax=0.9、下限CRmin=0.1、最大迭代次数G=1000、延拓系数α=0.3,β=5。在t=0 s时,给系统加入一个阶跃输入信号,并在仿真时间t=15 s时给系统加入一个阶跃干扰信号。为了验证AMDE算法优化PID控制方案的优越性,将其仿真结果与DE算法算法优化PID控制的仿真结果进行比较。常规PID控制、DE算法优化PID控制和AMDE算法优化PID控制下的3种不同的响应曲线如图6所示。

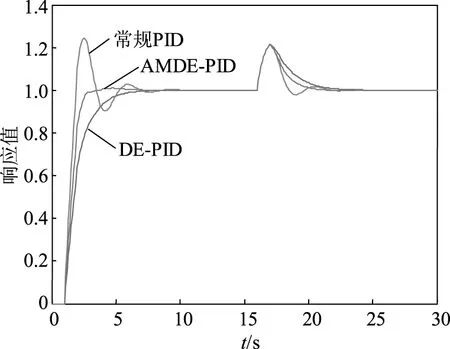
图6 模型参数匹配时3种控制方案阶跃响应曲线

图6中3种控制方案的阶跃响应曲线表明,AMDE算法优化PID控制方案的控制效果最好,超调量小,调节时间也相对较短,在稳态下抑制干扰的能力较好,可很快地达到平衡状态。DE算法优化PID控制方案控制效果较常规的PID控制方案好。常规PID控制超调较大,控制效果最次。3种方案具体的性能指标如表1所示。

在实际的DO浓度控制回路中,DO浓度的数学模型参数不可能是固定不变的,为了检验系统的鲁棒性,将对象比例增益R由0.5增加到0.55,惯性常数T由0.5增加到0.75,滞后时间τ由1增加到1.2,再用上述调整好的仿真模型对变化后的DO浓度数学模型进行仿真。3种控制方案的阶跃响应曲线如图7所示。

表1 3种控制方案模型参数匹配时性能指标

图7 模型参数失配时3种控制方案的阶跃响应曲线

图7中3种控制方案的阶跃响应曲线表明,在DO浓度的数学模型参数发生变化时,AMDE算法优化PID控制方案相较常规PID控制和DE算法优化PID控制同样具有较好的控制性能和鲁棒性。其结果充分证明了新的控制系统较常规PID控制系统在系统响应速度,超调量以及延迟时间、增强系统抗干扰能力等特性上均有明显优势。

5 控制系统实现及应用

本系统选用西门子S7—300系列PLC为开发平台[12]。在曝气池入水口和出水口处装设两台DO浓度测定仪,并以标准的(4～20)mA的信号上传到PLC的AI(模拟量输出)模块,通过OPC协议送入到MATLAB工作空间,经过MATLAB中的基于AMDE算法PID控制器处理,得出鼓风机变频器需要的频率大小。然后将结果通过OPC协议送回到PLC,经过AI模块输出到变频器,通过调节鼓风机频率的大小来调节鼓风量的大小,实现DO浓度的调节。根据工程实际,选择了2台罗茨风机(一用一备),为了实现变频控制的要求,选择2台MM430型变频器,该变频器是西门子专为风机、泵类负载设计的节能型变频器。监控功能由上位机实现,由西门子WINCC来实现,主要完成对现场DO浓度、变频器控制频率等的监控和初始值的设定以及对现场设备的开关控制等功能。

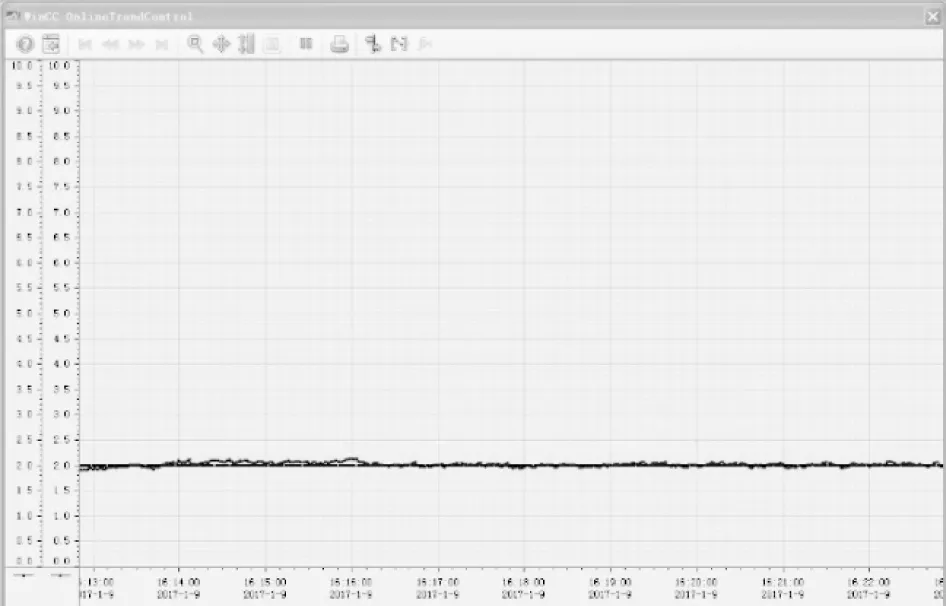
图8 DO控制系统实时运行曲线

本系统己在山东某造纸厂废水处理工段应用,图8为系统运行一段时间并稳定之后的DO浓度调节过程实时运行曲线。观察该图所示系统的调节效果,可以看出系统自调节能力很好,DO值基本稳定在2 mg/L左右基本能在较短时间内稳定在设定值,满足工程实际的需要。

6 结 论

本课题设计的基于自适应变异差分进化算法的曝气池溶解氧PID控制系统已在山东某造纸厂废水好氧处理控制系统中成功应用,并收到良好的控制效果。该系统结构简单、调节时间短、调节精度高、稳态性能好、超调量小,相较于常规PID控制能够很好的完成DO浓度的自动控制。当系统进水量为1700 m3/d、CODCr浓度为2058 mg/L,在该控制系统的作用下,CODCr去除率在84.5%,BOD去除率在93.4%,满足国家排放标准的出水要求。

[1] Kang Jia-yu. Research on modeling & control for pulp & paper wastewater biological treatment[D]. Xi’an: Shaanxi University of Science and Technology, 2011. 康家玉. 制浆造纸废水生物处理过程建模与控制[D]. 西安： 陕西科技大学, 2011.

[2] ZHANG An-long, PAN Hong-yan, FAN Di-Gang. Oxidation ditch process using low-pressure jet aeration system for the treatment of washing bleaching wastewater from a reed pulp mill[J]. China Pulp & Paper, 2010, 29(10): 34. 张安龙, 潘洪艳, 樊砥钢. 低压射流曝气氧化沟系统处理苇浆造纸中段废水[J]. 中国造纸, 2010, 29(10): 34.

[3] Du Xian-jun. Research on modeling optimization and control of activated sludge process in wasterwater biological treatment[D]. Lanzhou: Lanzhou University of Technology, 2013. 杜先君. 污水生物处理过程建模、优化与控制研究[D]. 兰州: 兰州理工大学, 2013.

[4] Xie Ji-rong, Wang Jia-wei. Study on optimization of aeration system based on cascade control of Do and air demand [J]. China Water & Wastewater, 2011, 21: 36. 谢继荣, 王佳伟. 基于溶解氧与需气量串级控制的曝气系统优化控制[J]. 中国给水排水, 2011, 21: 36.

[5] Carlos Alberto Coelho Belchiora. Dissolved oxygen control of the activated sludge wastewater treatment processusing stable adaptive fuzzy control[J]. Computers and Chemical Engineering, 37 (2012), 152.

[6] Zhong Wei-sheng, Ma Hong-jie, Wan Tao. Application of FNN-PID method based on GA to DO control[J]. Computer Measurement & Control, 2011(8)： 1908. 衷卫声, 马红杰, 万 滔. 基于遗传算法的FNN-PID控制技术在溶解氧控制中的应用[J]. 计算机测量与控制, 2011(8)： 1908.

[7] Shi Xiongwei, Qiao Jun-fei, Yuan Ming-zhe. Optimal control for wastewater treatment process based on improved particle swarm optimization algorithm[J]. Information and Control, 2011(5)： 698. 史雄伟,乔俊飞,苑明哲. 基于改进粒子群优化算法的污水处理过程优化控制[J]. 信息与控制, 2011(5): 698.

[8] Guan Feng, Tang Wei, Feng Qian, et al. Application of fuzzy expert control in pulping middle stage wasterwater aerobic treatment process[J]. Computer Measurement & Control, 2010(5): 1039. 关 锋, 汤 伟, 冯 茜, 等. 模糊专家控制在制浆中段废水好氧处理过程中的应用[J]. 计算机测量与控制, 2010(5): 1039.

[9] ZHANG Ai-juan, HU Mu-yi, HUANG Ya-nan. Dissolved oxygen concentration control system based on expert feed-forward and fuzzy PID feed-back control[J]. Transactions of China Pulp and Paper, 2016, 31(2): 43. 张爱娟, 胡慕伊, 黄亚南. 基于专家前馈-模糊PID反馈的溶解氧浓度控制方案研究[J]. 中国造纸学报, 2016, 31(2): 43.

[10] Liang Xi-ming, Zhou Wei, Li Shan-chun. Study of wastewater aeration system based on fuzzy control [J]. Control Engineering of China, 2012(2): 328. 梁昔明, 周 威,李山春. 基于模糊控制的污水曝气系统的研究[J]. 控制工程, 2012(2): 328.

[11] Xiaofen Lu, KeTang. A newself-adaptation scheme for differential evolution[J]. Neurocomputing, 2014, 146: 2.

(责任编辑：常 青)

Dissolved Oxygen Concentration Control System Based on the Adaptive Mutation Differential Evolution Algorithm

TANG Wei1,3BAI Zhi-xiong2,*GAO Xiang2

(1.CollegeofElectricalandInformationEngineering,ShaanxiUniversityofScienceandTechnology,Xi’an,ShaanxiProvince, 710021;2.CollegeofMechanicalandElectricalEngineering,ShaanxiUniversityofScienceandTechnology,Xi’an,ShaanxiProvince, 710021;3.ShaanxiResearchInstituteofAgriculturalProductsProcessingTechnology,Xi’an,ShaanxiProvince, 710021)

The parameter of dissolved oxygen is of great importance in the process of paper wastewater treatment. But the dissolved oxygen control process exists the problems of nonlinear and time-delay, the normal PID control is hard to get ideal effect. In this paper, based on the analysis of the differential evolution algorithm, an adaptive mutation differential evolution algorithm was proposed, and used to the parameter optimization of PID controller, in order to realize the dissolved oxygen concentration precise control. Through MATLAB simulation, compared with the normal PID control and the PID control based on the traditional differential evolution algorithm, this algorithm had the advantages of fast response, less overshoot and good control effect. In practical applications of this algorithm COD removal rate reached 84.5%, BOD removal rate reached 93.4%,Water treatment system was running well and the treated wastewater could meet the discharge regulation.

dissolved oxygen; PID; differential evolution algorithm; adaptive mutation

2017- 02- 23(修改稿)

陕西省重点科技创新团队计划项目(2014KCT-15)；咸阳市科技计划项目(2012K03- 01)。

汤 伟先生，博士，教授；主要研究方向：制浆造纸全过程自动化、工业过程高级控制、大时滞过程控制及应用。

TS736

A

10.11980/j.issn.0254- 508X.2017.06.010

*通信作者：白志雄,在读硕士研究生；主要研究方向：制浆造纸过程控制。