带限位器的冲击隔离器刚度计算模型
2017-06-29张明远冯麟涵
魏 来, 张明远, 计 晨, 冯麟涵
(1.沈阳工业大学 机械工程学院, 辽宁 沈阳110000; 2.海军装备研究院, 北京100161)
带限位器的冲击隔离器刚度计算模型
魏 来1, 张明远1, 计 晨2, 冯麟涵2
(1.沈阳工业大学 机械工程学院, 辽宁 沈阳110000; 2.海军装备研究院, 北京100161)
用数值方法模拟带限位功能的冲击隔离器一般采用双线性模型,即在限位器发挥作用前计算模型中的刚度为隔离器的冲击刚度,然而,众多研究表明,隔离器的静刚度、动刚度以及冲击刚度3者在数值上存在较大的差异。为探究2种计算方法在计算结果上的差异性,提高隔离器计算的准确性,对带限位器隔振装置的计算方法进行改进,将传统的双线性计算方法加以优化,采用多线性计算方法。建立结构模型,将隔离器以及限位器的接触部分简化为弹簧和阻尼器;选择合适的隔离器,加载与之相适应的冲击环境;对加速度和速度响应分别进行对比分析。得出结论:多线性计算方法与双线性计算方法计算结果有一定差异,多线性计算方法所计算的加速响应峰值较多线性方法有所降低,且振荡次数减少。多线性计算方法所计算的位移响应峰值略小于双线性计算方法的计算值,多线性计算方法使得响应脉宽出现先窄后宽的现象。
限位器;多线性计算方法;冲击环境;隔离器
0 引言
海军舰船在战斗时不可避免地会遭受水雷、鱼雷等敌方武器的攻击,由此产生的水下非接触爆炸一般不会击穿船体结构,却会造成舰用机电设备大范围的损坏,导致舰艇丧失生命力和战斗力。海上战例及实船爆炸冲击试验表明:机电设备是舰艇抗冲击能力的薄弱环节。舰用机电设备的冲击防护是各国海军十分关注的问题。采用隔离器来对设备进行防护是目前各国舰艇通常采用的方法,既可以起到减振降噪的作用,又可以隔离冲击。
由于隔离器的固有频率较低,在冲击载荷作用下,其产生的加速度响应较小而位移响应较大,甚至可能超出隔离器本身的变形极限,导致隔离器的弹性元件失效。因此,很多设备需要安装限位器来限制设备的位移。对于带限位器的冲击隔离问题,国内在带限位器的隔振系统抗冲击性能研究方面有所发展[1-2],汪玉等[2]通过有限元软件ANSYS建立带间隙的弹簧单元刚度矩阵, 用一系列的带间隙的弹簧单元叠加逼近限位器非线性刚度曲线和模拟限位器间隙,分析船舶设备非线性冲击响应。柳贡明等[3]建立了描述舰船柴油机双层隔振装置冲击响应的数理模型,并首次提出采用逐步积分法计算其响应。王官祥等[4]用模态分析方法对舰船设备的抗冲击性能进行了动力学仿真,该方法适用于论证和设计阶段及试验验收时对系统和设备进行抗冲击性能评估和预测。朱石坚等[5]提出一种计算具有3次方非线性刚度的单自由度隔冲系统最大响应的方法,将计算过程分成冲击作用阶段和自由衰减振动阶段。在冲击作用阶段中,认为系统的冲击刚度为常数;在自由衰减振动阶段中,考虑系统的刚度非线性,用迭代法推导出系统最大位移和最大加速度的一阶近似表达式。据此用数值计算的方法求出系统的最大位移和最大加速度。
现有资料[6-8]表明,用数值方法模拟带限位功能的冲击隔离器一般采用双线性模型,即在限位器发挥作用前计算模型中的刚度为隔离器的冲击刚度,在限位器发挥作用时,计算模型中的刚度为隔离器的冲击刚度与限位器刚度之和。然而,众多研究表明,隔离器的静刚度、动刚度以及冲击刚度3者在数值上存在较大差异。冲击发生时,隔离器虽然按照冲击刚度响应,然而极为短暂的冲击结束后,隔离器按照动态刚度响应,直到按静刚度平衡而静止。隔离器在冲击载荷结束后的动态响应过程,设备仍可能与限位器碰撞。因此,用双线性模型计算隔离系统的冲击响应是否会产生较大的误差,从而影响对设备冲击安全性的判断,仍未可知。
建议引入多线性模型,将隔离器的多线性刚度分为静刚度、动刚度和冲击刚度3段进行计算,并与双线性模型的计算结果进行对比。同时,加入带限位器计算模型,用于对比验证。
1 计算模型
1.1 结构模型建立
冲击隔离器上端与设备连接,下端固定在甲板上或设备的基座上。冲击隔离器的主体一般由橡胶或钢丝绳等弹性元件构成,其刚度和阻尼分别为K1、C1。为防止冲击过程中隔离器的弹性元件产生过大弹性变形,从而使用限位器。图1是带限位功能的冲击隔离器力学模型,图中:设备质量40kg,限位器的刚度和阻尼分别用K2、C2表示,预设定限位器的工作间隙U0= 30mm(双侧)。

图1 带限位的隔离器模型
1.2 隔离器选型
本文以带限位装置的6JX-400橡胶隔振器为研究对象,其力学性能参数:静刚度为285N/mm;动刚度为1 016N/mm;冲击刚度为1 650N/mm;z向额定载荷为4 000N;额定载荷下静变形为14mm±2mm;固有频率为7mm±1.5Hz;阻尼比为0.06;z向最大变形量为45mm。
1.3 多线性刚度力学模型建立
由于在冲击过程中系统的刚度矩阵是突变的(系统是非线性的),同时,由于橡胶不可被压缩,在冲击过程中,其刚度会随着不断被压缩而逐渐增大,在脱开过程中,其刚度则会逐渐减小,因此系统模型应当求导非线性刚度。带限位装置隔离器的双线性刚度曲线力学性能如图2所示,其中K1为隔离器计算刚度,K2为限位器刚度。结合6JX-400隔离器性能参数和限位器参数,带限位装置隔离器的多线性刚度曲线力学性能如图3表示,其中K3,K4,K5分别为隔离器的静刚度、动刚度和冲击刚度。此外,图2和图3中的刚度曲线为单侧刚度即拉伸刚度曲线,压缩刚度曲线与拉伸刚度曲线关于原点对称。
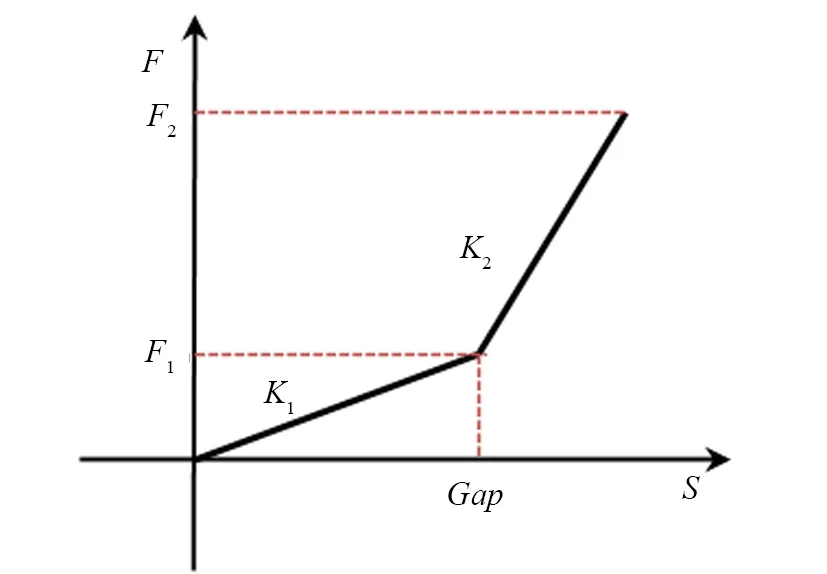
图2 双线性刚度曲线力学性能模型

图3 多线性刚度曲线力学性能模型
2 冲击环境
2.1 冲击响应谱
以弹簧振子的固有频率为横坐标,以最大响应为纵坐标绘制出冲击载荷的相对位移响应谱、伪速度响应谱和加速度响应谱,如图4所示。

图4 典型设计冲击谱
2.2 冲击输入
根据德国军标BV043-85中对设备冲击考核冲击环境的相关规定,将三折线谱转换为如图5所示双重正弦变化的冲击信号,该信号由正负2个面积相等的半正弦波组合而成,图5中横坐标为时间,纵坐标为加速度。

图5 双重正弦变化时间历程曲线
根据冲击响应谱,正半波的振幅约为谱加速度A0的二分之一,每个半波的面积约为谱速度v0的三分之二,此加速度历程经2次积分后得到冲击响应谱的最大相对位移D0,由此得到关系式(1)~式(5):
结合大量相关冲击试验的结果以及现有正负双波冲击机的承载能力,定制冲击环境主要参数如下:谱加速度A0= 800π;谱速度v0= 6m/s;谱位移D0= 5cm。
将A0、v0和D0这3个参数代入式(1)~式(5)中,计算得到双重正弦变化时间历程曲线中各个参数如下:a2= 400πm/s2;a4= 100πm/s2;t1= 5ms;t2= 20ms;v1=v2= 4m/s。
3 计算结果分析
3.1 双线性与多线性计算方法的位移响应
双线性和多线性计算方法在不同限位条件下的位移时间曲线如图6所示。从图6可以看出:在无限位装置的情况下,多线性计算方法所计算出的相对位移峰值略小于双线性计算方法的相对位移峰值,这是由于在没有限位器的情况下,设备的最大响应为

图6 位移响应曲线
而双线性计算方法中,刚度为隔振设备的冲击刚度。多线性计算方法中刚度为3个不同的值,其整体刚度可以理解为一个根据不同作用时间加权平均的刚度,从而造成加权后的刚度高于双线性计算过程中的固定刚度。
另外,通过对有限位和无限位2种情况下双线性和多线性的计算方法进行对比,发现多线性计算方法所得位移响应脉宽出现明显的先窄后宽,而双线性计算方法所得位移响应脉宽相对变化缓慢。在剧烈冲击阶段,隔离器发生较大变形,迅速达到冲击刚度;自由振荡阶段,由于阻尼存在,系统逐渐进入动刚度和静刚度起作用的阶段,刚度下降导致频率降低,因此出现上述先窄后宽的现象。双线性计算方法的刚度值恒定,导致其脉宽变化不大。
3.2 双线性与多线性计算方法的加速度响应
双线性和多线性计算方法在不同限位条件下的加速度-时间曲线如图7所示。在无限位器的情况下,采用双线性计算方法所计算出的加速度响应,其曲线更加平滑;而多线性计算方法所得出的加速度响应曲线,其恢复过程较快且加速度峰值较双线性计算方法略低,会更快地趋于平衡状态,但其波形由于采用多线性方法而出现过渡的痕迹。在有限位器情况下,仍然是多线性计算方法恢复过程较快且加速度峰值较双线性计算方法略低。

图7 加速度响应曲线
计算发现,在带限位器情况下,二次碰撞会使加速度响应明显增加,但其峰值依然低于输入加速度峰值。
4 结论
本文首先建立隔离系统结构模型,后通过对隔离器选型得到多线性刚度曲线,并采用非线性弹簧单元模拟具有非线性刚度的隔离器。计算结果表明:
(1) 多线性计算方法所计算的位移响应峰值要略小于双线性计算方法计算值,多线性计算方法使得响应脉宽出现先窄后宽现象。综合考虑加速度、位移响应,多线性计算方法所得响应更容易恢复平衡状态。
(2) 在同等条件下,多线性计算方法与双线性计算方法计算结果有一定差异,多线性计算方法所计算的加速度和位移响应的峰值较双线性计算方法有所降低,且振荡次数减少。
(3) 在一定的计算条件下,限位器会使二次碰撞后设备的加速度响应增加,同时增加系统振荡频率。
[1] 龚宪生, 谢志江,骆振黄,等.非线性隔振器阻尼特性研究[J].振动工程学报, 2001,3: 334-338.
[2] 汪玉, 胡刚义, 华宏星,等. 带限位器的船舶设备非线性冲击响应分析[J]. 中国造船,2003,2: 39-44.
[3] 柳贡民, 刘志刚.以逐步积分法计算舰船柴油机隔振装置冲击响应[J]. 哈尔滨工程大学学报, 1997,4: 19-24.
[4] 王官祥,汪玉.模态分析在冲击动力学分析中的应用[J].噪声与振动控制, 2001,3: 10-12.
[5] 朱石坚,何琳,翁雪涛.非线性隔冲系统最大响应的计算方法[J].海军工程大学学报, 2001,13(1): 11-13.
[6] 黄映云,何琳,谭波,等.橡胶隔振器冲击刚度特性试验研究[J].振动与冲击, 2006,1: 77-78.
[7] 赵应龙, 何琳, 黄映云,等.限位器对隔振系统抗冲击性能的影响[J]. 振动与冲击, 2005,2: 71-76.
[8] VALENTE A X, MCCLAMROCH N H, MEZIC I. Hybrid dynamics of two coupled oscillators that can impact a fixed stop[J]. International Journal of Nonlinear Mechanics,2003,38(5): 677-689.
Calculation Model of Shock Isolator with Limiter
WEI Lai1, ZHANG Mingyuan1, JI Chen2, FENG Linhan2
(1.Mechanical Engineering School, Shenyang University of Technology, Shenyang 110000,Liaoning, China; 2.Navy Equipment Research Institute, Beijing 100161, China)
Shock isolator with limiting function is simulated by bilinear model commonly, the stiffness of which is calculated as the impact stiffness of the isolator before the limiter works. However, many researches show that there is great difference in numerical value among isolator static stiffness, dynamic stiffness and impact stiffness. In order to explore the differences between the two calculation methods in the calculation results, and improve the accuracy of the isolator calculation, the calculation method of the vibration isolation device with limit device is improved. Traditional bilinear calculation method is optimized, and the method of multilinear calculation method is proposed. The structure model is established, and the isolator and contact part limiter are simplified as springs and dampers. After the selection of isolator equipment, adaptive impact environment is loaded. The acceleration and the velocity response are analyzed through the comparison of the output results. It can be concluded that there are some differences between the results of the multilinear calculation method and the bilinear calculation method. The peak value of the acceleration and displacement response calculated by the multilinear method is lower than the calculated value of the multilinear method. The multilinear method makes the response pulse appear the phenomenon of being narrow first and wide later and reduce the number of oscillations.
limiter; calculation method of multilinear; impact environment; isolator
青年科学基金“舰艇机械设备在瞬态冲击作用下的动力学模型可靠性研究(编号:51209215)
魏 来(1990-),男,硕士研究生,主要从事舰船设备抗冲击设计与研究
1000-3878(2017)03-0034-05
U662
A
