基于iBeacon的室内定位算法优化研究

林信川, 游贵荣

(1.福建商学院 信息管理工程系，福建 福州 350012；2.福建商学院 信息网络中心，福建 福州 350012)

基于iBeacon的室内定位算法优化研究

林信川1, 游贵荣2

(1.福建商学院 信息管理工程系，福建 福州 350012；2.福建商学院 信息网络中心，福建 福州 350012)

针对无线传感网络中室内定位算法定位精度不高、算法收敛慢的问题，依托基于BLE 4.0的iBeacon基站设备，为提升室内定位算法精度和效率，提出IIDWC定位算法。该算法结合基于测距的RSSI技术、加权质心算法和倒数距离加权插值定位思想，在确定多个广播重叠区域加权质心坐标及其权重系数的过程中，反复利用倒数距离加权插值方法，通过提升关键锚节点在确定加权质心坐标过程中的重要性，进一步优化权重系数，在仿真环境中提升了定位精度和收敛速度。通过合理设置锚节点的功率、通信半径、部署密度和测量时间，该算法的定位精度能够达到0.8 m，满足了多数室内定位场景的技术要求。

无线传感网络; iBeacon锚节点; RSSI; 加权质心

随着数据业务和多媒体业务的飞速增长，基于无线传感器网络(Wireless Sensor Networks，WSNs)[1]进行室内精确定位的技术已成为当前研究的一个新热点。室内节点定位作为无线传感网络的一项关键技术，其基本要求是获取室内节点的位置坐标。当前广泛使用的GPS定位技术主要应用于室外场景，对于室内定位场景，有可能出现多径现象导致定位结果不准确或无法定位。目前常用的室内定位技术有基于超声波、红外线、超宽带的定位技术和射频识别定位技术(WLAN、ZigBee)等。考虑到测量过程中，不同节点间的角度数据或距离数据的关联性，测距(range-based)算法和测距无关(range-free)算法[2]是比较常见的两类定位算法。前者在收集节点间的距离或角度信息的基础上，待测节点的位置可通过三边测量法、三角测量法或最大似然估计法[3]进行计算，RSSI、TOA、TDOA和AOA等[4]都是此类算法的代表，此类算法对硬件有一定要求，但定位精度相对较高。后者分析过程中不依赖于距离和角度数据，通常利用网络对通性等数据进行分析，常见的有质心算法、Amorphous算法和DV-Hop算法[5]等。虽然此类算法对硬件要求较低，但反射、散射和绕射现象往往对定位误差影响较大。

目前国内外研究者针对基于WSNs的室内定位算法和方案进行了大量研究。石欣等[6]提出了改进的RSSI多维标度室内定位算法，通过建立各节点信号强度的相异性矩阵，相继应用多维标度法、平面四参数模型记性坐标计算和转换、粒子群算法确定了优化参数，最终计算出移动节点坐标。余刨等[7]通过设定平均分布的三类基准点获取测试场景内具有不同定位标签的RSSI向量，在依据判定规则确定基准点后，利用无线信号室内传播模型得到移动权值，用于计算待测节点的坐标数据。李石荣等[8]提出了一种基于RSSI概率统计分布的加权K最近邻算法，利用SPD方法和SVM算法，进行指纹节点RSSI向量区间构建和K个近邻指纹点选择，并利用测试点RSSI向量到每个近邻指纹点的最小欧氏距离，通过WKNN算法获取定位结果。黄海辉等[9]提出了W-Centroid加权质心算法，采用测距倒数之和替代测距之和的倒数，并将其作为减小定位误差的权重，强化了关键节点的因子。丁恩杰等[10]提出了WR-Centroid算法，将RSSI与加权质心算法相结合，相较加权质心算法在提升定位精度的同时降低了通信节点的成本。刘云等[11]提出了WCBD算法，通过优化权重系数，加快了算法的收敛速度，进一步论证了其对于定位算法结果精度的重要性。

iBeacon是由苹果公司于2013年发布的基于低功耗蓝牙4.0(BLE 4.0)的技术，目前已普遍用于各类室内定位场景，但存在定位方式单一、定位精度不高的问题，且针对其定位精度和效率优化的研究成果较少。本文研究和仿真环境主要基于配备DA14850芯片的iBeacon基站设备，结合基于测距的RSSI技术、加权质心算法和插值定位思想，通过进一步优化iBeacon在室内通信过程中的权重系数，提出IIDWC算法。

1 RSSI测距技术

iBeacon的通信过程遵循无线电通讯模型，因此在本文将利用无线信号传播路径损耗模型中的对数-常态分布模型[12]进行研究。该模型定义如下：

PL(d)=PL(d0)+10nlg(d/d0)+ε,

(1)

其中d和d0为待测节点位于不同位置时与锚节点间的欧式距离，PL(d)和PL(d0)分别为传输距离为d和d0时的接收功率，其单位为dBm；n为信号的衰减因子，与无线传感网络环境密切相关；ε为一个均值为0且同时服从高斯分布的随机变量。在iBeacon室内定位技术中将d0固定为1 m，那么PL(d0)即为距离iBeacon锚节点1 m处的接收功率，对于采用确定芯片的iBeacon锚节点，其值将为固定值。可将以上传播模型简化为iBeacon在室内环境下的信号传播模型：

RSSI=T-10nlgd+ε,

(2)

其中T表示距离iBeacon锚节点1 m处的无线信号强度RSSI值，T和n需要通过对大量测量数据进行拟合后得到。当前位置与不同锚节点间的RSSI值可通过蓝牙终端测得，d为通过计算得到欧氏距离，以下分析中将其与实际距离进行比较进而确定算法误差。

2 加权质心定位算法模型

三角质心定位算法[13]和多边形质心定位算法[14]是基于RSSI的常见定位算法。加权质心算法[15]是在常见质心算法的基础上，利用待测节点和锚节点间距离信息值(RSSI值)，计算出该锚节点的权重系数，该值可用于衡量每一个锚节点对质心位置的影响力，并反映出待测节点和锚节点间的内在关系。

加权质心算法可以表示为：

(3)

其中(x,y)为待测节点的坐标，锚节点共N个，第i个的坐标为(xi,yi)，其中1≤i≤N，ωi为第i个锚节点对应的权重系数。常见的权重系数的取值为待测节点与锚节点之间距离d的函数，通常该函数满足d越大权重系数ωi越小的规律。若待测节点不在测量范围内，则相应锚节点的权重系数值为0。

3 改进的加权插值定位算法

本文提出的IIDWC(Improved Inverse Distance on Weighted Centroid)算法，是在倒数距离加权插值[15]的基础上，首先分别取得各锚节点位置与广播边界交点的距离倒数之和，作为确定广播重叠区域质心的权重系数，进而得到经过加权优化计算的该区域的加权质心坐标。通过上述所得的多个加权质心坐标，可反复利用倒数距离加权插值的方法，基于各锚节点的位置优化各加权质心的权重系数，最终可通过加权质心算法计算得到待测节点的理论坐标。此举进一步使距离较近的锚节点在定位过程中起到更加主要的作用，即锚节点与待测节点的距离越近，传播路径损耗值越小，在权重系数的计算过程中影响力就越大。这就避免了一些算法中非关键锚节点对定位结果产生的干扰。

首先在待测节点M(x,y)的四周部署4个iBeacon锚节点A、B、C、D，坐标分别为OA(xA,yA)、OB(xB,yB)、OC(xC,yC)、OD(xD,yD)，4个锚节点持续性地向待测节点M发送广播信号，d1为锚节点A与待测节点M间的欧式距离，d2为锚节点B与待测节点M间的欧式距离，d3为锚节点C与待测节点M间的欧式距离，d4为锚节点D与待测节点M间的欧式距离。

分别以其中的3个锚节点A、B、C为圆心，d1、d2和d3为半径作圆。假设3个圆存在广播重叠区域，且边界交点分别为O1、O2和O3。其中交点O1坐标(xO1,yO1)的计算方法为：

(4)

O2(xO2,yO2)和O3(xO3,yO3)的坐标值同理可得。以O1、O2和O3为顶点可构成一个三角形。多数研究方法通过求得的O1、O2和O3的坐标，利用三角质心算法得到该区域的三角质心坐标。此举未充分考虑待测节点与各锚节点之间的距离对后续定位算法精度的影响，因此本文也对该区域的质心坐标的计算过程进行了改进。

通过A、B、C三点和O1的相对位置，可得O1的优化后的权重系数为

(5)

其中dAO1、dBO1和dCO1分别为O1到锚节点A、B、C的欧式距离。同理分别将O2和O3视为待测节点，那么

(6)

则以O1、O2和O3为3个顶点的三角形区域的加权质心坐标N1(x1,y1)为

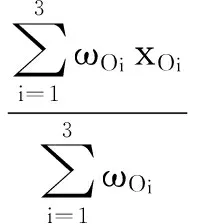
(7)

图1 定位模型

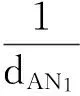
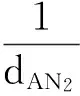
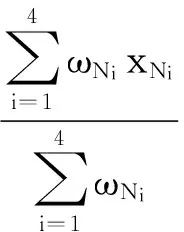
(8)

4 算法过程

4.1 算法步骤

由以上的定位模型分析，将本文提出的IIDWC算法的实现步骤归纳如下：

1)将待测节点部署在多个锚节点的广播范围内，已部署的多个锚节点均按照一定频率持续进行广播，其广播数据包中包含其ID及其位置信息；

2)待测节点对接收到的来自各锚节点的数据包进行滤波和数据拟合，根据iBeacon在室内环境下的信号传播模型，利用式(2)分别通过测得的RSSI值计算出待测节点与其附近锚节点的欧式距离；

3)将以上步骤求得的多个欧氏距离值按照升序排列，优先选取与待测节点距离最近的4个锚节点，若其中任意3个锚节点无法构成图1所示区域，那么可使用与待测节点间欧式距离更大的锚节点代替该节点，直到可构成图1所示区域为止；

4)利用以上步骤中4个锚节点中的任意3个进行待测节点定位，广播重叠区域交点的坐标通过式(4)可得，进而通过改进的加权插值定位算法求出重叠三角区域的加权质心坐标；

5)重复步骤(4)，将余下锚节点中的任意3个反复组合，可求得另外3个重叠三角区域的加权质心坐标；

6)通过式(8)对步骤(4)和步骤(5)中所得的4个加权质心节点，重复利用倒数距离加权插值定位算法，计算待测节点的理论坐标值；

7)比较待测节点的计算所得的理论坐标与实际坐标之间的误差。

4.2 误差分析

可通过公式(9)计算本算法的误差:

(9)

其中(x,y)和(xe，ye)分别为待测节点的实际坐标和理论坐标。若存在n个待测节点，则可通过平均误差E衡量本算法的精度，表述如下:

(10)

5 仿真分析

5.1 测距并拟合

选择一个80 m×80 m的空旷场所作为测试场所完成iBeacon传播模型的测定实验。首先将1个iBeacon锚节点固定在房间中的一个位置，然后分别距离该锚节点2、6、10、…、78 m处设置40个测试点，通过在每个待测节点处使用支持BLE 4.0的蓝牙设备采集RSSI值，每个测试点采集100组样本数据。反复采集80个不同锚节点的样本数据经处理后进行高斯滤波，将滤波后的样本的平均值作为该位置的RSSI值，最后使用MATLAB 2015b对RSSI值与距离值d之间的关系，通过式(2)进行拟合，拟合曲线如图2所示，得到拟合函数为：

RSSI=-20lgd-67。

(11)

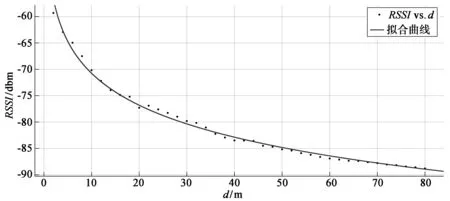
图2 RSSI值与距离d拟合关系

5.2 仿真论证

使用MATLAB2015b针对IIDWC算法进行仿真，实验环境相同。与一些分析过程中信号衰减因子n多以经验值进行假设分析不同，本文根据式(11)可知信号衰减因子n=2.0，信道中的随机高斯噪声在5～10之间。在80 m×80 m场所内分别均匀布置10、20、30、40、50、60、70、80个iBeacon锚节点，同时在该场所内随机选取100个点作为待测节点位置。对W-Centroid算法、WR-Centroid算法、WCBD算法和本文提出的IIDWC算法进行仿真，如图3—图5所示。

图3 平均误差随时间变化

图3在锚节点数量和锚节点通信半径固定不变的前提下，4种算法的平均误差虽然都随时间呈现出逐渐下降并最终收敛的趋势，但IIDWC算法的收敛速度明显快于其他3种算法，在28 s后基本收敛，且最终收敛后的平均误差达到1.4 m，与其他3种算法相比，定位精度明显提高。

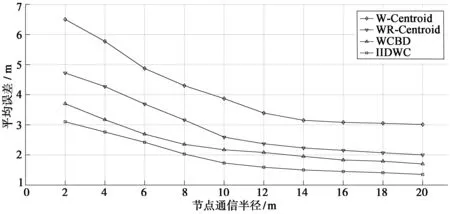
图4 平均误差随通信半径变化

图4在锚节点数量和采样间隔时间固定不变的前提下，通过逐步调整锚节点的通信半径，4种算法的定位精度都不断提高并呈现收敛的趋势。IIDWC算法的平均误差值均小于其他3种算法，且在锚节点通信半径达到10 m时平均误差已收敛于1.7 m以内，随着锚节点通信半径增加，其该算法的定位精度还将进一步提升。

图5在锚节点的通信半径设定为30 m且采样间隔时间固定不变的前提下，通过增加均匀部署的锚节点的数量，可以有效提升4种算法定位的精确度。当均匀部署的锚节点的数量达到45个时，IIDWC算法的精度已经控制在1 m以内，较之误差仅次于该算法的WCBC算法定位精度提高了41.6%。在锚节点数量多于50个时，平均误差明显开始收敛，其收敛时机要早于其他3种算法。

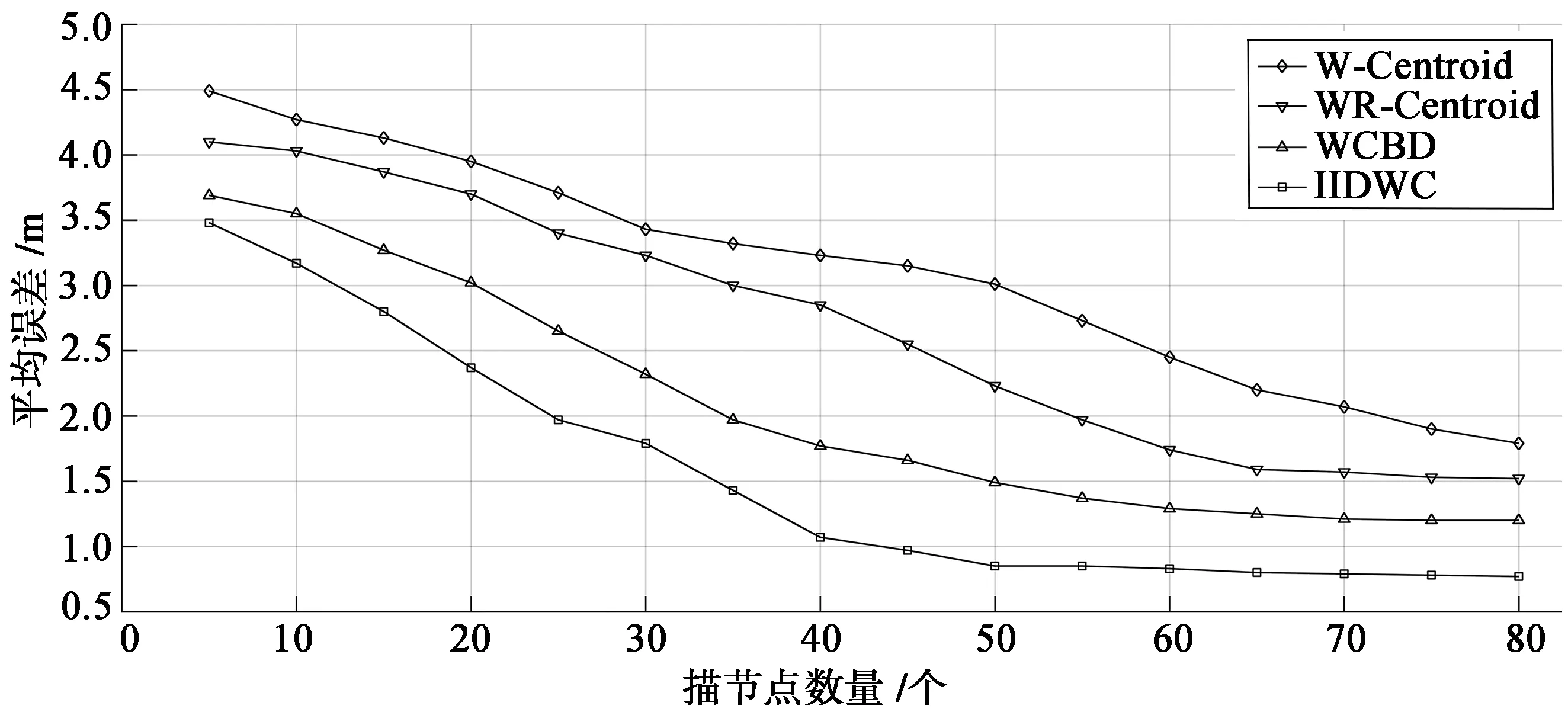
图5 平均误差随锚节点数量变化

6 结 语

无线传感网络中室内定位算法研究的主要问题集中在如何提升算法的定位精度以及收敛速度两个方面。本文基于iBeacon技术，结合RSSI技术、加权质心算法和倒数距离加权插值定位思想，利用定位过程中起主要作用的锚节点与待测节点的位置关系，优化了加权质心坐标及其权重系数的计算方法，提出了IIDWC算法。由仿真结果可知本算法在同等条件下，较其他定位算法具有更快的收敛速度和更高的定位精度。在后续的工作中，准备将本算法应用于实体的室内定位项目，以进一步验证和改进，为以后的空间精确定位算法起一定的指导作用。

[1] 马晓贤,彭力.一种改进的无线传感器网络DV-Hop定位算法[J].计算机工程与应用,2015,51(21):97-101.

[2] 郄剑文,贾方秀,李兴隆,等.基于组合测距的无线传感器网络自定位算法[J].传感技术学报,2016,29(5):739-744.

[3] 金艳,李曙光,姬红兵.基于柯西分布的跳频信号参数最大似然估计方法[J].电子与信息学报,2016,38(7):1696-1702.

[4] 张怡,席彦彪,李刚伟,等.基于卡尔曼滤波的TDOA/AOA混合定位算法[J].计算机工程与应用,2015,51(20):62-66.

[5] 向满天,王胜,杨友华.基于阈值机制与距离校正的WSN改进DV-Hop定位算法[J].传感技术学报,2016,29(6):920-926.

[6] 石欣，印爱民，陈曦.基于RSSI的多维标度室内定位算法[J].仪器仪表学报,2014,35(2):261-268.

[7] 余刨，战荫伟.基于RSSI的移动权值定位算法[J].计算机应用研究,2016,33(5):1450-1452.

[8] 李石荣,李飞腾.基于RSSI概率统计分布的室内定位方法[J].计算机工程与应用,2016,52(11):119-124.

[9] 黄海辉,李龙连.WSN中一种基于RSSI的移动节点改进定位算法[J].电子技术应用,2015,41(1):86-89.

[10] 丁恩杰，乔欣，常飞，等．基于RSSI的WSNs加权质心定位算法的改进[J]，传感器与微系统，2013，32(7)：53-56．

[11] 刘云,刘菁原.基于RSSI的加权质心定位算法优化研究[J].华中师范大学学报(自然科学版),2016,50(3):358-362

[12] 尹海峰.基于移动信标节点的无线传感器网络定位算法设计[D].南京：南京理工大学,2014.

[13] 赵大龙,白凤山,董思宇,等.一种基于卡尔曼和线性插值滤波的改进三角质心定位算法[J].传感技术学报,2015(7):1086-1090.

[14] 崔法毅,邵冠兰.基于RSSI多边定位误差的加权质心定位算法[J].红外与激光工程,2015,44(7):2162-2168.

[15] 樊子德,李佳霖,邓敏.顾及多因素影响的自适应反距离加权插值方法[J].武汉大学学报(信息科学版),2016,41(6):842-847.

[责任编辑：张存凤]

Study on optimization of indoor location algorithm based on iBeacon

LIN Xin-chuan1,YOU Gui-rong2

(1. Department of Information Management and Engineering,Fujian Commercial College,Fuzhou 350012,China;2. Information Network Center,Fujian Commercial College,Fuzhou 350012,China)

Aiming at the problems of low localization accuracy and slow convergence of wireless sensor networks,this paper proposes a newly improved algorithm named IIDWC based on iBeacon technology to improve the precision and efficiency. This algorithm is based on RSSI ranging technology,weighted centroid algorithm and inverse distance weighted interpolation ideas. In the process of determining multiple broadcasts overlapped the weighted centroid coordinates and their weights,by repeatedly using the inverse distance weighted interpolation method,it optimizes the weight coefficient,and promotes the weight of key anchors for calculating the weighted centroid coordinates. In the simulation environment by setting power,communication deployed RADIUS,density of anchor nodes and the measurement of time,localization accuracy of the algorithm can achieve less than 0.8 m. It can meet the requirements for the indoor location project.

wireless sensor networks; iBeacon anchor node; RSSI; weighted centroid

2096-3998(2017)03-0067-07

2016-11-21

2017-03-13

福建省教育厅A类基金资助项目(JA15730)

林信川(1981—),男，福建省福州市人，福建商学院讲师，硕士，主要研究方向为物联网、移动互联网构建；游贵荣(1974—)，男，福建省龙岩市人，福建商学院副教授，主要研究方向为智能信息处理。

TP212.9； TP391

A