极限学习改造稀疏自动编码机及其在故障诊断中的应用

宋坤骏 林建辉 丁建明 西南交通大学

极限学习改造稀疏自动编码机及其在故障诊断中的应用

宋坤骏 林建辉 丁建明 西南交通大学

传统栈式稀疏自动编码机的全局权值微调算法基于反向传播，由于深度神经网络损失函数的非凸性质，反向传播算法极易陷入局部极小值，且前几层网络的权值往往得不到充分训练。为此引入极限学习算法到深度神经网络的训练中来，将多个通过二阶Hessian-Free方法训练后的稀疏自动编码机层叠起来，然后通过正则化ELM算法确定最后输出层的权值。结果表明二阶Hessian-Free方法克服了最速下降法存在的锯齿型收敛问题,并保留了牛顿方法计算Hessian矩阵的时间和空间开销。将机车振动数据分别用离散傅里叶变换和量子傅里叶变换转换到频域后作为特征输入网络,检测结果表明网络的泛化能力和训练速度都有了可观的提升。

极限学习；稀疏自动编码机；滚动轴承；故障

1 引言

机车走行部中的滚动轴承是故障频发的一个部件。目前各种故障诊断方法在提取特征的时候主要基于人工经验或专家知识，例如简易诊断中，主要选择了时域波形峭度系数参数、加速度有效值参数两个指标作为故障判断参数，精密诊断方法则进一步考虑了故障的特征频率，利用不同零部件故障的特征频率不同实现故障定位。这些人工选取的特征能够满足多数场合下故障诊断系统的需要。但通常轴承及转向架的故障模式复杂，实际信号中各种噪声混杂，普通的信号处理方法除需要提取特征外，还要过滤各种噪声，而有研究表明机器学习算法中加入噪声实际上起到了一种正则化的作用，可以增加网络的泛化性能。因此噪声如何去除，以及去除多少实际上是相当需要技巧的一门学问。基于深度学习理论的去噪自动编码机可以自动学习一些特征并能在学习特征过程中自动完成降噪。可以说是达到了噪声消除和提高泛化能力之间的平衡，同时省去了研究各种去噪算法的精力和计算特征的耗时。

当前在故障诊断领域类似极限学习的快速学习算法和类似深度学习的无需先验知识的特征学习方法的研究包括：严文武等人采用独立成分分析(ICA)提取故障特征，并用ELM算法进行工业过程故障分类,通过与概率神经网络和支持向量机等的对比研究表明ICA-ELM方法有更快的训练速度和更高的分类准确率。秦波等人先对信号进行EMD分解，然后提取与原信号相关度较大的IMF分量的能量作为特征向量送入BP、SVM、PSO-SVM与 GA-SVM和ELM等分类器中，通过对比试验证明了ELM方法在实时性和准确率上都胜过上述传统机器学习算法。庞荣等人将离散傅里叶变换后的转向架故障信号送入降噪自动编码机进行特征学习，并将学到的特征送入BP神经网络进行故障辨识，对转向架关键部件非全拆故障识别正确率能够达到100%。

此外本文分别用经典快速傅里叶变换和量子傅里叶变换将机车振动数据转换到频域后再输入所得深度网络，对比结果表明量子傅里叶变换能够有效削弱噪声对于信号特征提取的干扰，显著减少网络的输入维数。

2 代价敏感学习

通常机器学习算法的损失函数不论是交叉熵还是误差平方和损失函数都没有体现出不同类别间的代价敏感性,而在实际应用特别是故障诊断中，不同类别错分类的代价恰恰是差异悬殊的。例如漏判故障远比将正常情况误判为故障工况的损失要大。本文引进代价敏感性的方法是取加权误差平方和作为损失函数,其对应的最优权值可由加权最小二乘法求出解析解。加权最小二乘线性回归问题中系数的最优估计由下式给出

这里矩阵H∈Rm×m的第i行第j列元素（1≤i≤m.1≤j≤m）为第j个基函数hj在第i个采样点xi上的取值，W是各个权重组成的对角矩阵diag（W1，W2，...，Wm），而Z是函数采样值向量。是自变量采样点向量α2，...，αm）是各个采样点对应的叠加系数组成的向量。

加权最小二乘法的损失函数为最小的充分必要条件是HTWH是正定矩阵。

假设给定特征x的条件下，样本属于类Ci的几率是P(Ci| x)，那么将该样本归为类Cj的风险等于条件损失L（Cj|Ci）关于上述条件几率的加权和。

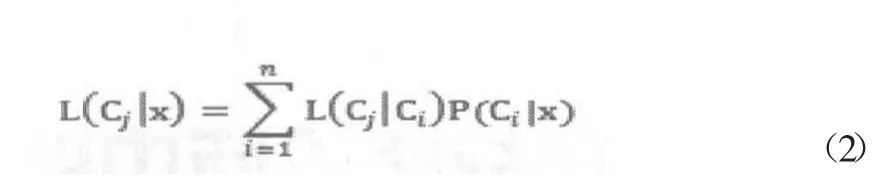
代价敏感性体现在对于固定的i和流动的j，损失函数 L（Cj|Ci）是不同的。条件损失矩阵L（Cj|Ci）是预先给定的算法输入，这跟神经网络的权值是通过后天训练得到的是不同的。因此说任何不包含先验信息的损失函数 (例如上面的交叉熵损失函数)都不可能体现代价敏感性。为将损失函数改造成代价敏感的，可在原有损失函数基础上引进权重因子，其中的权重Wi可以理解为几率P（Ci|x）。已知交叉熵损失函数是专门为解决迭代学习权值过程中收敛速率饱和的问题而设计出来的一种损失函数，但是如果能够直接求出最优权值的解析解，那么就不存在迭代学习的必要了，因而此时选用误差平方和代替交叉熵函数也是可以的，以下小节中就是这么做的。

3 极限学习机理论

极限学习机是一种新型的单隐层前馈神经网络训练算法，其输入层的权值和偏置参数是随机指定的无需通过迭代计算得到，因此其计算效率较传统BP网络有了大幅提高，同时其泛化能力没有下降反而有所提升。最原始的ELM算法流程十分简单，其输出层表达式为

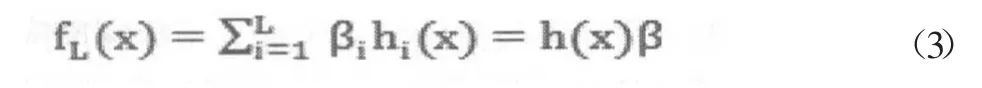
这里h(x)=[h1(x)，h2(x)，...hL(x)]是隐含层激活函数向量，第i个分量函数hi(x)同隐藏层第i个神经元的权值和偏置参数(ai，bi)有关。而β=[β1，β2，...，βn]是待求的隐藏层输出权值，由如下最小二乘问题求出：

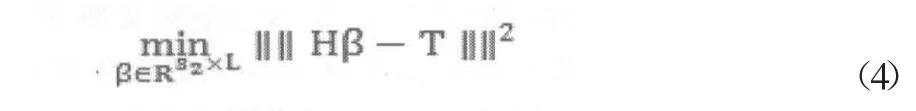
Bartlett关于前馈神经网络泛化能力的研究表明：众多满足误差范数最小的最小二乘解中，回归系数向量的范数越小，则网络的泛化能力越好，因此满足权值平方和最小的Moore-Penorse最小二乘解是所有最小二乘解中泛化能力最好的，取其为ELM隐层输出权值的计算公式如下

这里关于m个输入样本的隐层输出矩阵定义为

而关于m个输入样本的训练数据目标矩阵则由下式定义

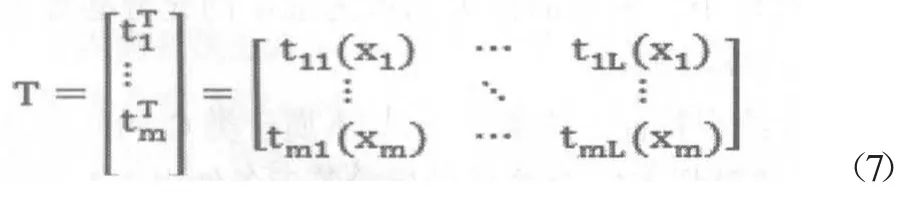
上述基于经验风险的算法可能存在对样本数据的过拟合，为此加入一项正则化项到ELM损失函数的表达式中，同时将上一小节的加权最小二乘理论加以运用以改造损失函数提现代价敏感性，最终得到代价敏感正则极限学习机输出层权值的公式为

其中I是维数等于隐层神经元数目的单位矩阵。

4 稀疏去噪编码机理论

深度表示学习中一种常见的无监督学习算法是稀疏自动编码机，表示的稀疏性是指隐藏层的输出神经元中大多数神经元的值都低于激活阈值，通常利用平均激活度

来表达，其输出表达式为

其中hw,b(x)=[h1(x→),h2(x→),...,hm(x→)]是输出层向量，其第i个分量为

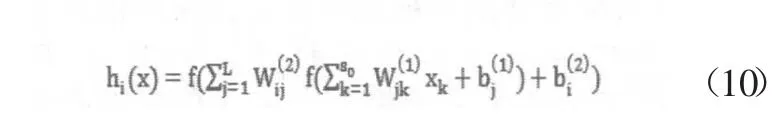
这里我们取激活函数f为tanh函数，相比sigmoid函数来说，在权值更新时没有同步增大和同步减小的偏向性。为体现出稀疏性约束,只需添加一项基于KL-Divergence的惩罚项惩罚过大的激活度即可，由此得到完整的损失函数为

5 量子傅里叶变换

通常需要将原始时域信号变换到频域作为特征输入神经网络中进行故障诊断。变换方法可以是经典傅里叶变换也可以是量子傅里叶变换。量子傅里叶变换充分利用了量子力学的态叠加原理，使得在一次变换中可以同时完成所有变换系数的计算。相比经典傅里叶变换其计算速度能有指数级别的增加。

QFT对于任意量子位态矢的作用由如下态叠加式定义

式中n=2m,而m是量子态位数，态 代表信号的数值，其在基础矢量展开式上的展开系数就等于整数j的二进制表示中的各位数字，这些数字取值只能为0或1，而 的量子傅里叶变换后所得态矢量在同一组基础矢量上的展开式系数则可以取复数值。

上述量子计算方法的过程如下所示：

①初始化：将输入输出寄存器都初始化为0

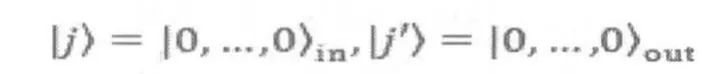
②for时刻t=0到p，do：

③振动信号转为量子态表示：为与量子线路兼容，需将采集到的振动信号以二进制表示，并放置在输入输出寄存器中

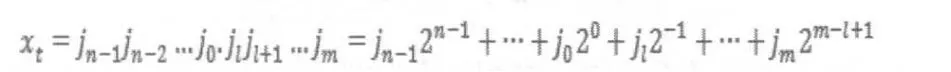
为避免对整数和小数部分分别进行量子傅里叶变换，上述振动信号统一取小数点后l位，再将所有采样点上测量数值乘以10l化为整数。这个预处理的开销很小，但是能够显著降低算法的执行时间。

④QFT变换：每一制备的量子态 ，实施QFT变换，得到，并存储在寄存器out中

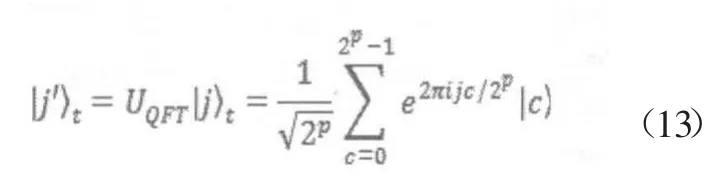
其中p=m+n是量子位数，量子态 的数目为2p。上式同时完成了2p-1次计算。

⑤特征提取：对输出寄存器的量子态 ，进行测量，使其塌缩到固定值，得到对应样本的概率分布，其公式为

图5和图6所示为量子傅里叶变换后所得频谱，为了比较的方便已和经典傅里叶变换所得频谱归一化到同一标度，由图可见，量子傅里叶变换能够更加凸显出信号的特征频率，将输入网络的特征取为概率幅度大于0.5的概率幅值对应的频率后可以看到，量子傅里叶变换提取的特征频率对应的概率幅值比起经典傅里叶变换给出的功率幅值更能体现出信号中的干涉效应，能够达到消除噪声更加良好的结果。然而量子傅里叶变换最大的优势还是在于其计算的并行性质，以及阈值设定的便利性和显著的特征降维效果。

虽然量子算法提取出的特征比起经典傅里叶变换少了许多，但是由于其所得特征同故障关联度较高，因而网络的训练速度不但没有下降反而有所上升，且分类准确率也有所上升。说明量子傅里叶变换在并行计算大大改善网络训练速度的同时能够有效提高网络的预测性能。

6 基于极限学习的栈式稀疏自动编码机

实验所取栈式稀疏自动编码机模型的参数如下表1所示。

表1 SDAE模型参数

将前一稀疏自动编码机的隐层输出作为后一个稀疏自动编码机的输入即得栈式稀疏自动编码机，直接套用代价敏感正则化ELM输出层公式求出栈式稀疏自动编码机中最后一层的输出权值最优解为 (假设一共有N层隐藏层)

上式中H是最后一层隐藏层的输出矩阵。

上述稀疏自动编码机的输出还需要送入分类器进行故障识别和分类。这里选用的分类器是另一个代价敏感的正则化极限学习机，同时还选用了其他分类器如支持向量机，BP算法训练的单隐层神经网络做对比研究，研究结果请参见下一小节。

7 实验数据分析

将上述算法应用到滚动轴承的故障诊断中，采用的数据为青岛四方机车厂的振动加速度数据。采样频率为10 kHz，采样时段为机车速度从30 km/s加速到100 km/s的过程，在30 km/s、50 km/s和100 km/s各采集10 s的振动数据。分别测量横向、纵向和垂向三个方向的加速度分量。故障模式分为外圈内面故障和滚柱烧蚀故障两种。原始信号数据先做归一化处理。然后再做离散傅里叶变换得到频域特征后送入深度网络进行学习。

将每一故障信号分成多段，每段含有256个数据点作为一个样本。取前2/3的数据作为训练集，取后1/3数据作为测试集。训练集和测试集均由两个轴承两种故障工况信号样本混合而成，均先进行离散傅里叶和量子傅里叶变换得到频域表示后再送入极限学习机进行辨识。仿真得到两种故障工况下时域信号波形如图1、图3所示；频域信号波形如图2、图4所示；量子傅立叶变换后所得频谱如图5、图6所示。

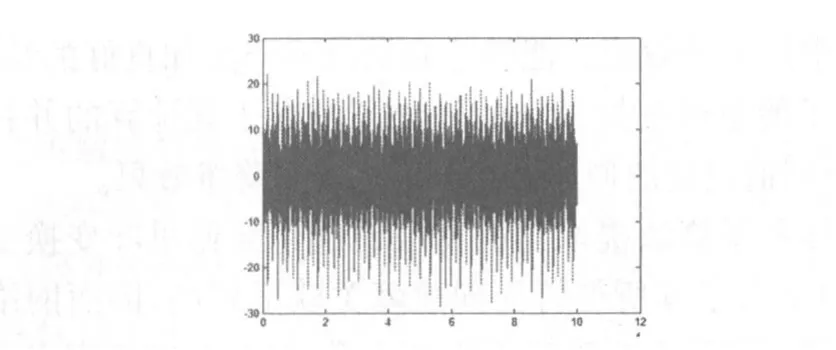
图1 外圈内表面故障工况下轴承时域振动波形

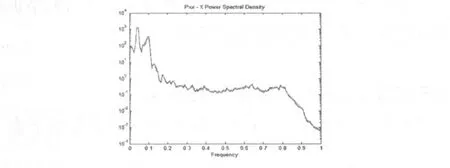
图2 外圈内表面故障工况下轴承频域振动波形(垂向加速度)

图3 滚柱烧蚀故障工况下轴承时域振动波形(垂向加速度)

图4 滚柱烧蚀故障工况下轴承频域振动波形(垂向加速度)

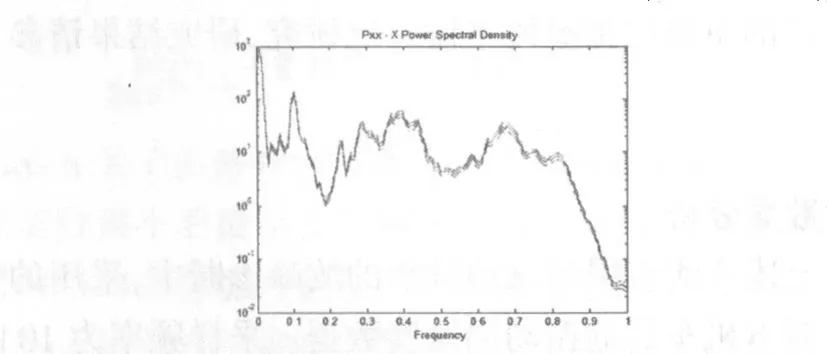
图5 外圈内表面故障工况下量子傅里叶变换后所得频谱(垂向加速度,已将概率幅值归一化为同经典快速傅里叶变换同一标度)

图6 滚柱烧蚀故障工况下量子傅里叶变换后所得频谱(垂向加速度,已将概率幅值归一化为同经典快速傅里叶变换同一标度)

对比量子傅里叶变换提取的特征和经典傅里叶变换提取的特征可以知道量子变换算法能够更加有效地凸显频谱的中频段部分,对于故障特征频率发生在中频段的故障不失为一种很好的特征提取算法。

将变换后频谱输入如表2所示3种故障模型中训练，可得各次实验故障识别率和运行耗时，从中可见各种算法的识别率以ELM-SAE为最高,SVM次之，而传统的BP算法最低,而在运行耗时上批量式的ELM算法最低，其次是在线式的ELM和SVM，最慢的是批量式的BP算法。

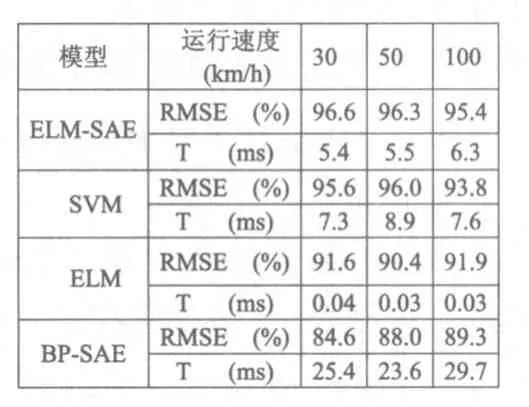
表2 各次实验的故障识别率和运行耗时

图7所示为模型深度同隐藏层神经元数的关系，由图可见，随着隐层神经元数目的增加，模型预测准确率基本呈现单调增加趋势。

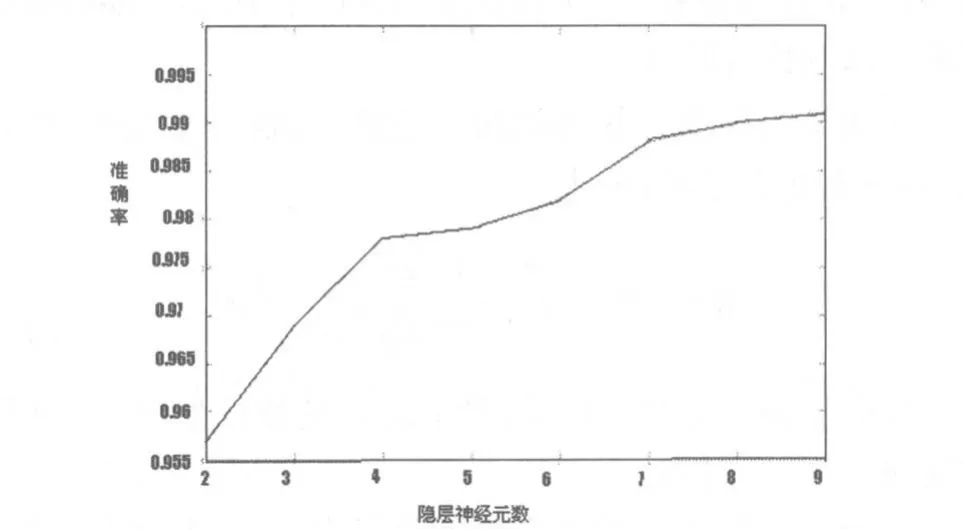
图7 模型准确率同隐层神经元数关系

8 结束语

本文将极限学习机同稀疏自动编码机有机结合，利用极限学习算法的性能优势很好地改进了堆叠稀疏自动编码机的训练速度，同时也免除了反向传播算法容易陷入局部极小的缺点。此外本文分别利用经典傅里叶变换和量子傅里叶变换算法提取特征,结果表明量子算法能够同时对比实验结果表明所提出的算法相比其他一些传统算法有效地改进了训练的准确度，不失为一种较为实用的在线故障诊断算法。

[1]Martens J Deep learning via Hessian-free optimization[C] International Conference on Machine Learning.2010：735～742.

[2]Vincent P,Larochelle H,Bengio Y,et al.Extracting and composing robust features with denoising autoencoders[C]//International Conference. 2008：1096～1103.

[3]Daniel J W.The Conjugate Gradient Method for Linear and Nonlinear Operator Equations[J].Siam Journal on Numerical Analysis,1967,4(1)：10～26.

[4]Bartlett P.The sample complexity of pattern classification with neural networks：the size of theweights is more importantthan the size of the network[J].IEEE Transactions on InformationTheory.1998,44(2)：525～536.

[5]Vincent P,Larochelle H, Lajoie I, et al. Stacked Denoising Autoencoders：Learning Useful Representations in a Deep Network with a Local Denoising Criterion[J].Journal of Machine Learning Research, 2010,11(12)：3371～3408.

[6]Zhenbing Zhao,Ning Liu,and Le Wang."Localization of multiple insulators by orientation angle detection and binary shape prior knowledge."IEEE Transactions on Dielectrics and Electrical Insulation, 22(6),2015：3421～3428.

[7]何星,王宏力,陆敬辉,等。基于优选小波包和ELM的模拟电路故障诊断[J]。仪器仪表学报,2013,34(11)：2614～2619。

[8]严文武,潘丰。基于ICA-ELM的工业过程故障分类[J]。计算机工程, 2015,41(10)：290～294。

[9]秦波,刘永亮,王建国,等.基于极限学习机的滚动轴承故障诊断方法[J].组合机床与自动化加工技术,2016(5)：103～106.

[10]庞荣,余志斌,熊维毅,等.基于深度学习的高速列车转向架故障识别[J].铁道科学与工程学报,2015(6)：1283～1288.

[11]潘峰,赵海波.Online Sequential Extreme Learning Machine Based Multilayer Perception with OutputSelfFeedback for Time Series Prediction[J].Journal of Shanghai Jiaotong University(Science),2013,18 (3)：366～375.

责任编辑：许耀元

来稿日期：2017-02-17