基于KPCA遗传算法的预报模型及其应用

王崇荣，阚海玉，静丽贤，陈丽芳

(1.华北理工大学 以升创新教育基地，河北 唐山 063210；2.华北理工大学 理学院，河北 唐山 063210)



基于KPCA遗传算法的预报模型及其应用

王崇荣1，阚海玉1，静丽贤1，陈丽芳2

(1.华北理工大学 以升创新教育基地，河北 唐山 063210；2.华北理工大学 理学院，河北 唐山 063210)

核主成分分析(KPCA)；遗传算法(GA)；RBF神经网络；健康度评价

针对数据的相关性、网络参数初始化的随机性对神经网络模型效率和精度的影响，本课题提出采用核主成分分析和遗传算法，优化RBF神经网络结构和参数。首先，采集与人体健康度有关的指标，应用核主成分分析对其进行降维处理；然后，针对RBF网络初始权值、扩展常数设置随意性大的不足，用MATLAB编程实现遗传算法对RBF网络初始参数的优化，并用收集到的数据进行模型的训练和仿真；最后，将该模型与未进行网络优化的模型进行比较。分析和对比表明，该预报模型消除了指标间的相关性，并且提高了预报精度和速度，为预报问题的处理提供了新的研究思路。

随着人们生活水平的不断提高，自身健康受到越来越多的关注。如何构建健康评价体系，全面客观地反映个体健康状况，已成为重要的研究课题。因此，构建体质健康综合评价系统具有重大的指导意义和现实意义。

王国军[1]引入模糊数学法对人体体质健康进行综合评价，解决了评价标准在大面积推广和使用时部分指标临界点上下数值相差不大但等级相差很大、与事实不符的问题。刘励[2]采用层次分析法和模糊综合评价进行个体健康评价。刘秀伶[3]等利用扩展的卡尔曼滤波辅助方法进行预处理及特征提取，将模糊逻辑引入神经系统，设计了一种基于动态生理信息融合的健康评价系统。刘伟[4]针对在健康评价中评价信息的模糊性和随机性，提出了基于自然语言的多属性群决策云模型集结方法。

分析学者们的健康评价体系，均将人体健康状况进行了有效的量化。但忽略了影响人体健康状况指标间的相关性，并且模糊数学的引入具有很大的主观性。本项目提出了人体健康评价体系模型，通过应用KPCA，消除了影响人体健康状况指标间的相关性；引入RBF神经网络对人体健康程度进行预测，消除了模糊数学的主观性。并且应用遗传算法优化神经网络参数，使网络避免陷入局部极小值，获得了更高的预报精度。

1 基本理论

1.1 核主成分分析(KPCA)

KPCA[5,6]是一种基于核函数的能够有效地解决非线性问题的主成分分析方法。它将原变量空间 通过一个非线性变换 映射到高维特征空间 ，在特征空间进行内积运算后提取特征值和特征向量再进行降维。

1.2 遗传算法

遗传算法[7](Genetic Algorithm)是一种启发式算法。其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和良好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向。

1.3 RBF神经网络

RBF神经网络[8,9]只有一个隐层，且隐层神经元与输出层神经元的模型不同。隐层节点激活函数为径向基函数，其净输入是输入向量与节点中心的距离(范数)而非向量内积，且结点中心不可调。结点的非线性变换把线性不可分问题转化为线性可分问题。输出层节点激活函数为线性函数。

隐层节点参数确定后，输出权值可通过解线性方程组得到，RBF网络结构如图1所示。

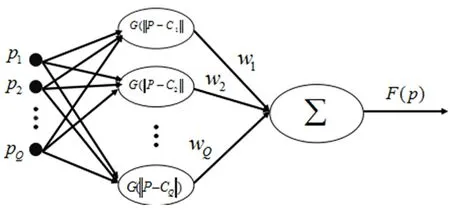
图1 RBF网络结构

2 模型构建

首先将核主成分分析后的分量作为RBF网络的输入[10,11]，其次用遗传算法优化的权值和扩展常数确定RBF网络的参数[12,13]，并对网络进行训练，然后进行网络仿真，测试模型的精度，最后通过和未经优化的模型进行对比，对模型的性能进行评价。建模流程如图2所示。

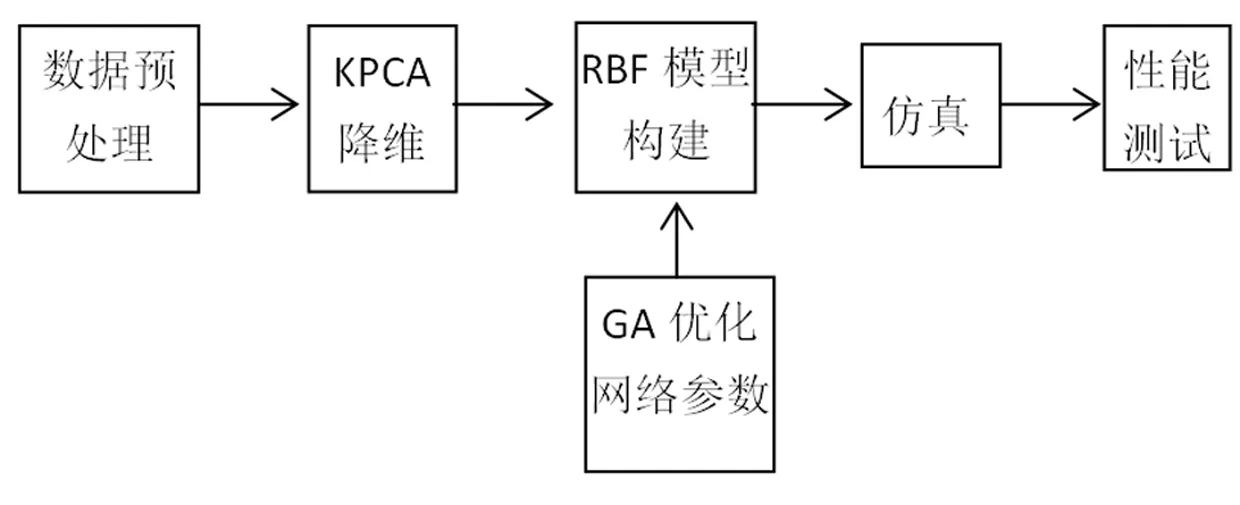
图2 基于KPCA遗传算法的RBF网络建模流程

2.1 数据分析与预处理

对数据进行核主成分分析(KPCA)，提取计算核主成分分量；降低输入的维数，简化RBF神经网络结构。

(1)输入原始数据X；

(2)将原始数据进行标准化处M理：

(1)

其中:

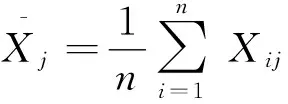
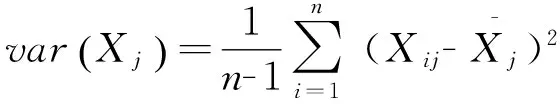
(2)

(3)将核函数映射到高维空间，得到矩阵K

(4)求解原矩阵K的转置矩阵K'，

K'=K-AijK-KAij+AijKAij

(3)

(4)

(5)计算矩阵K'/n的特征值λi(i=1,2…m)和特征向量vi(i=1,2…m)；

(6)找出m个主元对应的特征值λr和特征向量vr(i=1,2…m)；

(7)求出特征值的贡献率和累积贡献率；

(8)利用提取的核主成分作为输入输出综合指标。

2.2 遗传算法优化RBF网络参数

RBF神经网络在开始训练前将隐藏层到输出层的连接权值随机初始化为[0,1]之间的值，这种未经过优化的随机初始化会使RBF神经网络的收敛速度慢，且容易陷入局部最优解。采用遗传算法优化可以对初始权值、扩展常数进行优化，使RBF神经网络具有更高的精度。

初始化遗传算法参数，需要初始化的参数有最大迭代次数maxgen、群体规模sizepop、参数个数D、选择算子、交叉算子、交叉概率Pc、变异概率Pm.

根据实际求解的问题确定RBF神经网络的拓扑结构，建立网络初始模型；并根据网络的拓扑结构，计算待优化参数的个数D：

D=hiddennum*outputnum+1，其中，hiddennum和outputnum分别为RBF神经网络隐层节点数和输出层节点数。

输入网络的训练样本，将遗传算法待优化参数按照顺序组成一个向量，作为RBF网络连接初始权值、扩展常数，进行网络训练，计算实际输出和预测输出的均方误差，并以均方误差作为目标函数。

目标函数表示为:

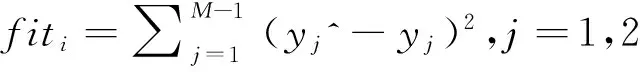
(5)

式中，为训练输出值；yj为训练期望输出值；

遗传算法优化RBF神经网络建模如下：

(1)读取前面步骤中保存的数据data；

(2)对数据进行归一化处理；

(3)参数设置；

(4)对种群进行实数编码，并将预测数据与期望数据之间的误差作为适应度函数；

(5)循环进行选择、交叉、变异、训练RBF神经网络,计算适应度，直到达到进化次数，或精度满足设置要求，停止循环操作；

(6)用得到的最佳权值和扩展常数构建RBF神经网络；

(7)用测试数据测试神经网络，并将预测的数据反归一化处理；

(8)分析预测数据与期望数据之间的误差。

3 人体健康评价模型

3.1 数据收集与处理

通过对50份体检数据整理筛选，去除异常数据。得到47份数据作为样本，部分样本如表1所示。

表1 部分原始数据表

健康度是用来定量描述人体健康水平的数值，影响健康度的指标主要有营养、中毒、免疫抑制、过敏、炎症、耗散。

3.2 KPCA优化网络输入

将数据归一化后，利用Cross-Validation方法，选取不同的核函数，经多次试验，采用指数型径向基核函数

(6)

当σ>200时，累计贡献率趋近于稳定，并且在选取的所有核函数中为最大，达到89.5%。图3所示为当σ∈[1,1 000]时累计贡献率。

图3 当 时累计贡献率

将营养、中毒、免疫抑制、过敏、炎症、耗散分别记为 。

此时选出的分析主元有2个：

F1=0.0164x1+0.3290x2+0.4556x3+0.7352x4+0.2987x5+0.2328x6

(7)

F2=0.1421x1+0.3881x2+0.4098x3+0.3174x4+0.2782x5+0.6950x6

(8)

3.3 遗传算法优化RBF神经网络参数

RBF学习的3个参数：

(1)基函数的中心ti；

(2)方差(扩展常数)σi；

(3)隐含层与输出层间的权值wij。

当采用正归化RBF网络结构时，隐节点数即样本数，基函数的数据中心即为样本本身，参数设计只需考虑扩展常数和输出节点的权值。

根据KPCA得到的结果，隐含层为2个神经元，可以计算出粒子的维数D=2*1+1=3。

选取40组新的数据作为训练样本。经多次试验，误差最小时，得到的平均误差为8.3%。

此时GA的基本参数为：

(1)群体规模sizepop=10；

(2)粒子维数D=3；

(3)最大迭代次数maxgen=100次；

(4)选择操作采用保留最优个体的随机采样法；

(5)交叉操作采用均匀的交叉算子，交叉概率为 ；

(6)变异概率为pm=0.1-[1:1:sizepop]×0.1/sizepop；

(7)终止条件：循环达到终止迭代次数或最优适度值连续迭代500次，计算结果差值小于0.000 01；

(8)群体适应度函数使用预测值和输出值的均方误差来定义。采取每15次显示1次网络参数，在第54次时得到全局最优结果。寻优结果动态如表2所示。

表2 寻优结果动态

3.4 仿真验证和预报

选取剩余的7组数据进行仿真。得到平均相对误差为9.2%。将仿真结果与原始数据进行对比。得到误差如图4所示。

图4 KPCA-GA-RBF网络仿真误差图

4 效率对比分析

为进一步评价KPCA-GA-RBF网络模型的仿真效果，与采用传统的BP神经网络模型、KPCA-BP网络模型分别进行训练仿真。

(1)单纯RBP网络预报：经多次试验，在RBF网络进行训练均方差最小时，扩展常数为0.45；训练精确度为0.000 01。

(2)KPCA-RBF网络模型预报：用KPCA进行数据预处理，将原来的6个指标综合成2个指标后，在RBF网络进行训练均方差最小时，扩展常数为0.52；训练精确度为0.000 01。

在3个模型分别达到最优时，用剩余的7组数据进行仿真，相对误差对比如图5所示。

图5 3个模型精度对比图

由图5可以看出，RBF、KPCA-RBF和KPCA-GA-RBF网络预测的相对误差分别浮动在30%、25%和15%以内。KPCA-GA-RBF模型相对误差明显优于其它2个模型，说明了模型在预测精度上的优越性。

模型训练性能对比结果如表3所示。

表3 模型训练性能对比表

由表3可以看出，KPCA-GA-RBF网络训练步数仅仅为54时就已经收敛，而KPCA-RBF网络和单纯的RBF网络，在训练步数达到最大时还未收敛，证明了KPCA-GA-RBF网络在收敛性上的优越性。因此，对于同一组学习样本集，应用KPCA-GA-RBF网络混合算法，能够大大减少迭代次数，加快训练速度。

对比分析表明：与传统RBF方法和KPCA-RBF神经网络法相比，该项目所研究的方法具有输出稳定性好、收敛性快、预测精度高等优点，将KPCA结合遗传算法，对RBF网络预报模型进行精简和优化，大大缩短了训练时间，提高了训练效率和预报精度。

5 结论

(1)分析了影响预报模型效率和精度的主要原因：数据的相关性和网络初始参数设置的任意性，提出通过应用KPCA，实现数据的降维，从而精简网络结构。

(2)应用遗传算法优化参数，使网络避免陷入局部极小值，从而获得更高的预报精度和更快的预报速度。从模型优化的角度，具有一定的理论意义和应用价值，为指导人们的生产生活提供了理论依据。

[1] 王国军.健康管理理念下公务员体制健康评价系统的研究与应用[D].上海：上海体育学院,2013.

[2] 刘励.儿童青少年健康的综合评价及影响因素研究[D].武汉：华中科技大学,2009.

[3] 刘秀伶,杨国杰,王洪瑞.动态生理信息融合在人体健康评价系统的应用[J].计算机工程与应用.2010,46(16):226-228.

[4] 刘伟.基于BIA的人体健康监测与智能评价系统研究[D].合肥，合肥工业大学,2013.

[5] 高宏宾,候杰,李瑞光.基于核主成分分析的数据流降维应用[J].计算机工程与应用.2013,49(11):105-110.

[6] 赵丽红,孙宇舸,蔡玉，等.基于核主成分分析的人脸识别[J].东北大学学报(自然科学版).2006，27(8)：847-850.

[7] 张启义,邱国庆,寇学智，等.两阶段遗传算法在求解TSP问题中的应用[J] 解放军理工大学学报(自然科学版),2011,12(1): 79-83(1): 12-15.

[8] 蒋吉丽.基于BP神经网络的强对流天气预报模型研究[J].电子科技大学，2010，03(2):11-29.

[9] 王兰霞.基于RBF神经网络的PM10污染预测研究[D].西安：西安建筑科技大学，2008.

[10] 孙志娟,赵京,戴京涛.采用KPCA-BP神经网络的并联机构全局综合性能评价方法研究[J].现代制造工程,2014,11(11):18-24.

[11] 李琳娜.基于核主成分分析(KPCA)和神经网络的单目红外图像深度估计[D].上海：东华大学,2013.

[12] 李敏强,徐博艺,寇纪淞.遗传算法与神经网络的结合[J].系统工程理论与实践.1999(12):16-20.

[13] 李勇,李妍琰.改进粒子群优化BP神经网络的洪水智能预测模型研究[J].西南师范大学学报(自然科学版),2014,05(19):75-80.

Prediction Model Based on KPCA and Genetic Algorithm and Its Application

WANG Chong-rong1,KAN Hai-yu1,JING Li-xian1,CHEN Li-fang2

(1.Yi-sheng Innovation Education Base,North China University of Science and Technology,Tangshan Hebei 063210,China;2.College of Science,North China University of Science and Technology,Tangshan Hebei 063210,China)

kernel principal component analysis; genetic algorithm; RBF neural network; health degree evaluation

Based on the correlation of data and the accuracy and efficiency of predicting model under the influence of network parameters initialization randomness,the Kernel Principal Component Analysis (KPCA) and Particle Swarm Optimization (PSO) algorithm were put forward to optimize neural network structure and parameter and improve the efficiency and precision of the forecast model.First of all,the KPCA was applied to the acquisition of indicators related to human health,reduce the data dimension and eliminate the correlation between attributes,which makes the selection of influence factors more scientific and reasonable,and the model structure more compact.Then,in view of the default of initialization parameter setting arbitrary in BP network large,RBF neural network was applied to optimize network initial parameters,so as to avoid early convergence of premature in network learning process in local minimum values.MATLAB was applied to realize the training and simulation of the model.The analysis and comparison results show that the prediction model constructed through the method can eliminate the correlation among the indexes,and greatly improve the forecasting precision and speed.It provides a new research approach for solving the prediction problems.

2095-2716(2017)03-0109-07

2016-12-26

2017-05-06

华北理工大学校级大学生创新创业训练计划项目(X2016303)。

O242.1

A