修正S变换与常规时频分析方法的对比

阮清青，张会星，王 昊，李凯瑞

(中国海洋大学 海底科学与探测技术教育部重点实验室，山东 青岛 266100)



修正S变换与常规时频分析方法的对比

阮清青，张会星，王 昊，李凯瑞

(中国海洋大学 海底科学与探测技术教育部重点实验室，山东 青岛 266100)

地震信号往往是非线性、非平稳信号，基于平稳信号理论的常规傅里叶变换方法不能刻画任一时刻的频率成分，而时频分析技术能同时展示信号在时间域和频率域的局部化特征。修正S变换作为一种较新的时频分析方法，是针对S变换窗函数相对固定、时频分辨率不能调节的问题提出的。通过对修正S变换与常规时频分析方法如短时傅里叶变换(STFT)、小波变换(WT)和S变换的对比，分析了修正S变换在时频分析方法中的作用。根据合成信号以及实测地震记录的时频分析可知：修正S变换较常规的时频分析方法具有更好的时频分辨率和能量聚集性，更有利于对非平稳信号的处理。

时频分析；修正S变换；S变换；小波变换；短时傅里叶变换

0 引言

在地震勘探中，地震波的传播会受到不同的岩性、物性和含流体地层的影响，导致地震信号具有非线性、非平稳特征，即实际地震资料的频谱成分及信号的各种统计特性是随时间而变化的。传统的傅氏变换是一种整体变换，只能了解信号在时间域或者频率域的全局特征，无法起到时频定位作用。时频分析( Time-Frequency Analysis)作为一种新兴的信号处理方法，它将信号从时间域变换到时间-频率域，不同频率分量的时间关联特性能够在时频平面上有效地表示出来，而且信号在任意时刻的能量都聚集在瞬时频率附近，其逆变换则可以得到等效的时间信号[1]。在时频分析研究和发展的短短几十年时间里，它已经在地震勘探数据分析的多个方面得到了重要的应用[2-5]。

常用的时频分析方法有短时傅里叶变换、S变换、小波变换、Wigner-Ville分布等[6-9]。短时傅里叶变换(STFT)是通过滑动时窗来计算其频谱，因而它的时间分辨率和频率分辨率受Heisenberg测不准原理约束[10]。小波变换继承了STFT局部化分析信号的思想，但选取的是窗口形状可变的窗函数，在分析时变非平稳信号时较STFT具有更理想的效果。1996年，美国地球物理学家Stockwell[7]综合了短时傅里叶变换(STFT)和小波变换(WT)的特点，首次提出了一种加时窗傅里叶变换方法——S变换，以较高的时频分辨率而备受关注[11-13]。S 变换是对短时傅里叶变换和连续小波变换的继承与发展，它综合了两种变换的优点，却弥补了它们的不足。然而，S变换具有时间和频率的分辨率不能同时提高的问题，而且标准S变换高斯窗口随频率的变化固定，导致其时频谱的时间分辨率较低[14]。

由于S变换的基本小波是固定不变的，使得S变换的应用受到限制，许多学者通过改进基本小波或窗函数得到了改进的S变换，并取得了良好的应用效果[15]。Mansinha 等[16]用(f/r)代替f，得到调谐的高斯函数，允许使用者自定S变换在时频面上时间和频率的分辨率。Pinnegar 等[17]提出用非对称的双曲窗代替高斯窗，用于地震波的P波首波时间的判定。高静怀等[18]用4个待定参数的调幅简谐波来代替S变换中的基本小波，用于薄层及薄互层的地震探测。陈学华等[19]引入调节参数λ和p对S变换的窗函数进行改造，用于信号的提取和抑噪。Duan Li和John Castagna[20]在2013年提出一种修正的S变换新方法，对标准S变换中的高斯窗函数进行改进，利用一个线性频率方程代替高斯窗的频率，调节时窗宽度随频率呈反比变化的速度，提高了S变换在具体应用中的实用性和灵活性。本文将修正S变换与常规的时频分析方法进行对比分析，通过对几种合成信号的频谱分解，研究修正S变换在时间分辨率、频率分辨率和能量聚集性方面的特点。

1 时频分析算法

1.1 短时傅里叶变换(STFT)

Dennis Gabor[6]针对傅里叶变换在时频分析的不足，提出了短时傅里叶变换。其基本思想是：引入一个时间局部化的窗函数，假定信号在窗函数内是平稳的，采用傅里叶变换分析窗内的信号，以确定窗内存在的频率成分，在信号时间方向移动窗函数，得到频率随时间的变化关系，即所需要的时频分布。短时傅里叶变换的定义为：

(1)

式中：x(t)为输入信号，f是频率，g(t)为窗函数，不同的窗函数得到的时频分布也不相同。

1.2 小波变换(WT)

小波变换继承和发展了短时傅里叶变换的局部化思想，同时又克服了窗口大小不随频率变化的缺点，是处理时变非平稳信号比较理想的工具，该方法分别采用了窄时窗及宽时窗对高频及低频信号进行处理。信号f(t)的小波变换定义[8]为：

〈f(t),Ψa,b(t)〉

(2)

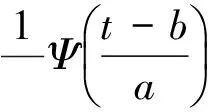
1.3 S变换(ST)

Stockwell[7]在前人研究时频分析方法的基础上，提出了S变换。S变换组合了短时傅里叶变换和小波变换的优点,同时也克服了它们的不足,采用与频率有关的可变高斯窗函数,而基本小波不必满足容许性条件。时域连续信号h(t)的S变换定义如下：

(3)

式中：h(t)为信号时间函数，f为频率，t为时间，τ控制高斯函数在时间轴上的位置。e-i2πft是傅里叶变换为S变换的振荡部分提供的指数函数，当τ随着时间移动时它不随规范化高斯窗口变化。

在S变换中，高斯窗函数和基本小波分别定义为：

(5)

由式(4)可知，S变换采用宽度可变的高斯窗函数,其时窗宽度随频率f呈反比变化。低频时，时窗较宽，从而获得较高的频率分辨率；高频时，时窗较窄，故可获得较高的时间分辨率。

1.4 修正S变换(MST)

对某一非平稳信号进行时频分解，由于S变换的窗函数是以固定的趋势随频率变化的，所以获得的时频谱是唯一的，其时频分辨率有限，因此需要对高斯窗进行改进[21-23]。为提高S变换对信号的时频分辨率，在高斯窗中加入一个调节参数δ，δ为频率的一阶线性方程：

δ(f)=mf+n

(6)

其中，m、n为常数，共同控制高斯窗的宽度，m、n两个参数均为正数，即调节参数δ随着频率f的增大而线性增大。

高斯窗函数则变为：

(7)

将式(7)代入式(3)得到修正后的S变换的表达式[20]：

(8)

信号经修正S变换得到的是一个时频二维矩阵，行代表时间，列代表频率。根据Heisenberg测不准原理，变换无法实现时频分辨率同时提高，可以通过优化选取参数m、n的数值，获得较高的时频分辨率。

2 时频分析方法对比

为了从时间分辨率、 频率分辨率和能量聚集等方面比较各种时频分析方法的应用效果，利用短时傅里叶变换、小波变换、S变换以及修正S变换方法分别对合成信号进行时频分析。

图1是不同频率的雷克子波合成的理论地震记录，主频从20～70Hz，得到的时频谱如图2。从图2a～图2d可以看出， STFT的分辨率较为单一，而且成像模糊，能量较为分散。虽然小波变换和S变换都具有多分辨率分析的特点，但对比两者发现小波变换的时间分辨率不如S变换。选取参数m=1,n=12得到信号的修正S变换时频谱，和其他三种方法进行对比，发现修正S变换较其他三种变换在时间和频率分辨率上皆有提高，高低频主频明显分辨，且在低频(10～20Hz)处，MST的时间分辨率提高显著，能量也更为集中，消除了相邻频率造成的干扰，效果更好。

图3是人工合成的地震信号，该信号由四种频率成分组成：15Hz、20Hz、30Hz、50Hz，采样点数为1024，采样时间间隔是0.002s。对比4种方法的时频谱图(图4a～图4d)可以看出：短时傅里叶变换虽然可以给出信号的联合时频特征， 但由于时间窗函数固定，直接导致其时间和频率分辨率是固定不变的，整体上呈现分辨率较低现象，这对低频和高频信号的检测是很不利的；而小波变换结果则呈现多分辨率分析的特点，但频散较为严重，与S变换相比存在一定的差异；由于S变换采用的高斯窗函数可以根据信号的频率不同做不同调整，即高频段采用高斯窗函数较窄，低频段采用高斯窗函数较宽，因此在时频谱上与短时傅里叶变换和小波变换相比，其时间分辨率和频率分辨率都有明显的改善；而修正S变换作为S变换的一种改进，通过调整参数m、n的值来控制高斯窗口的宽度，使得其时频谱在低频段的时间分辨率得到与S变换相比有明显提高(如在0.4～0.5s，两个能量团分开)，相邻频率的干扰有一定的抑制作用。因此，修正S变换在时间分辨率和频率分辨率上较短时傅里叶变换、S变换和小波变换等线性时频分析方法具有更佳的时频聚集性，可以更好地适用于非平稳地震信号的分析。

3 实际资料计算对比

图5是实际采集的一道地震记录，该地震记录有5000个采样点，采样时间间隔为0.4ms。分别用STFT、WT、ST和MST时频分析方法对该记录进行了时频特性分析(图6a～图6d)。从图6a～图6d中可以看出，短时傅里叶变换和小波变换虽然容易得到时频分析谱，但是它们的时频分析精度较低，短时傅里叶的分辨率单一。S变换采用的是随频率可变的窗函数，分别利用宽时窗和窄时窗在低高频时分析信号，得到的时频分析谱(图6c)较好地改善了时频局部化精度，较STFT和WT具有更高的时频分辨率。 MST时频分析方法基于ST的优良性质， 并修正了其时窗的缺陷， 使得MST在时频谱(图6d)的分辨率高于STFT、WT和ST。对比图6a～图6c与图6d，在图6～图6c中，位于1.6s处与1.7s附近的能量团黏连在一起区分不开；而通过优化参数(m=4/3,n=10)后的MST时频谱时间分辨率明显提高，黏在一起的能量团不仅区分开来(1.6～1.7s处)，而且整体具有更好的时频聚集性，这更有利于地震资料的处理和解释。

图1 雷克子波合成信号Figure 1 Ricker wavelet signal

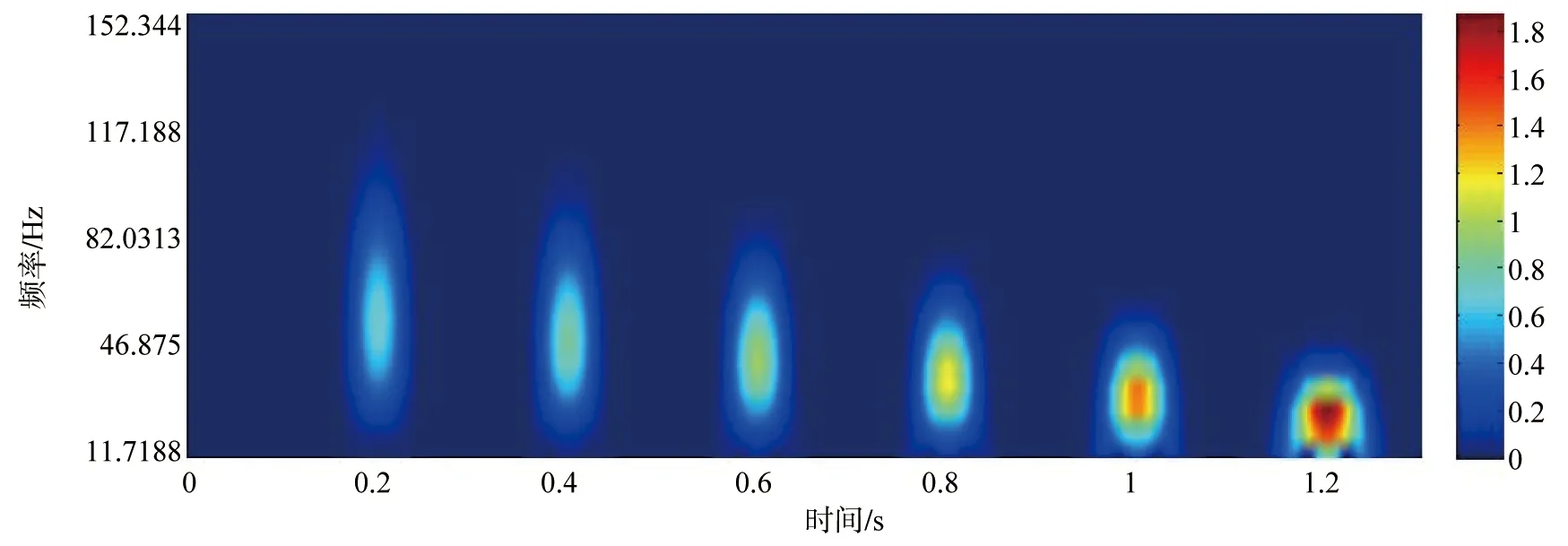
(a)stft时频图

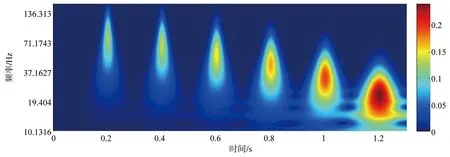
(b)小波时频图

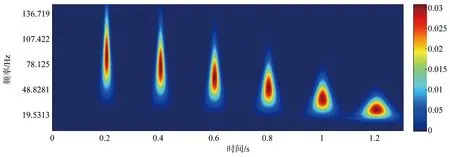
(c)S变换时频图

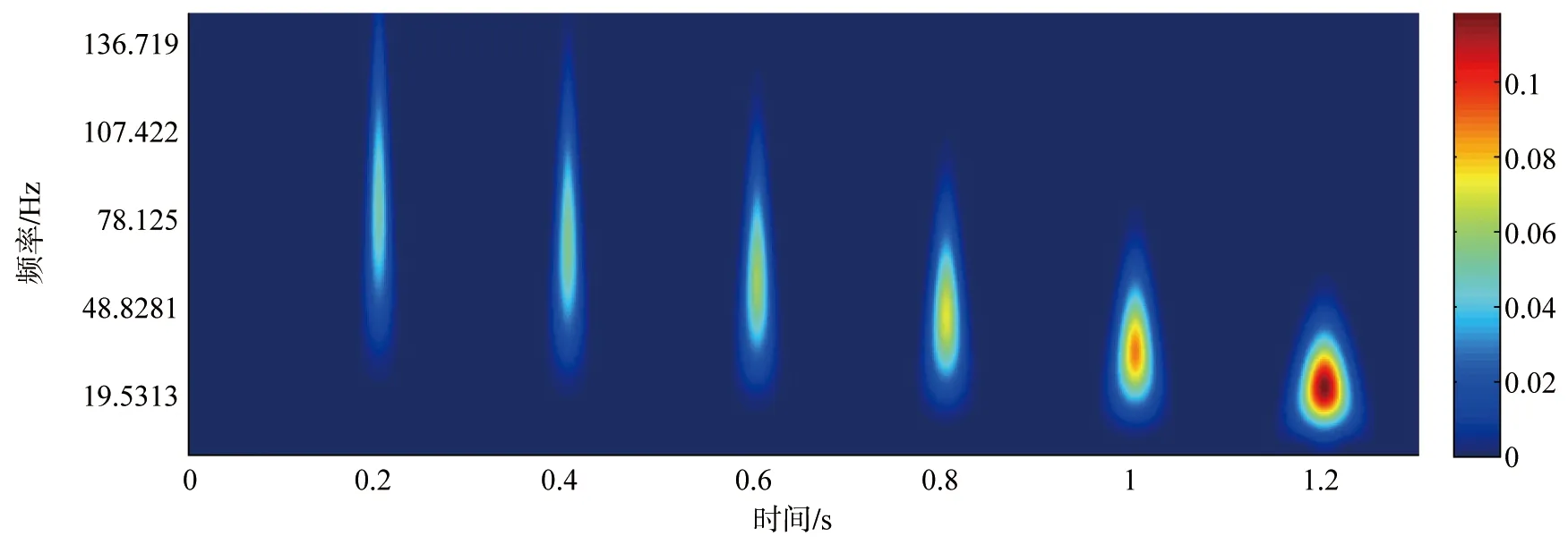
(d)MST时频图图2 雷克子波合成信号时频谱Figure 2 Time-frequency spectrum of Ricker wavelet synthetic signal

图3 人工合成地震信号Figure 3 Synthetic signals

图4 人工合成地震信号时频谱

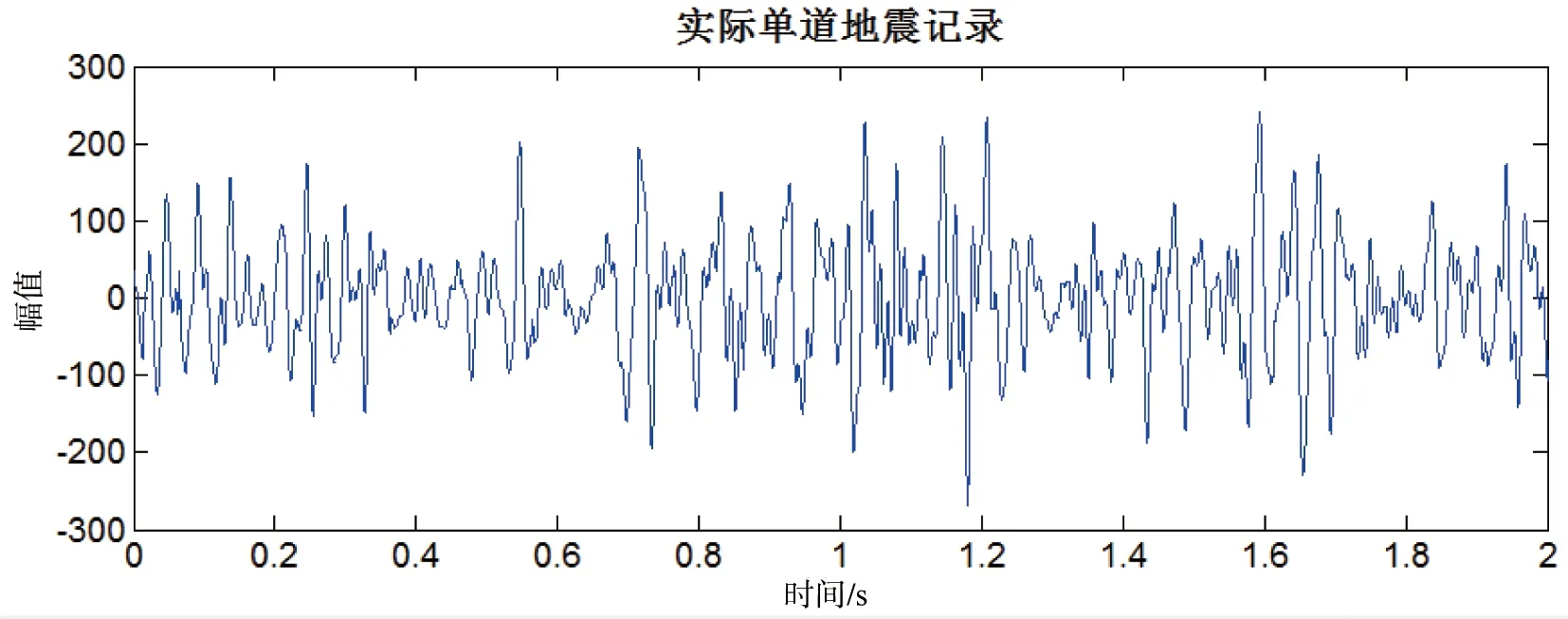
图5 实际单道地震记录Figure 5 Actual single channel seismogram

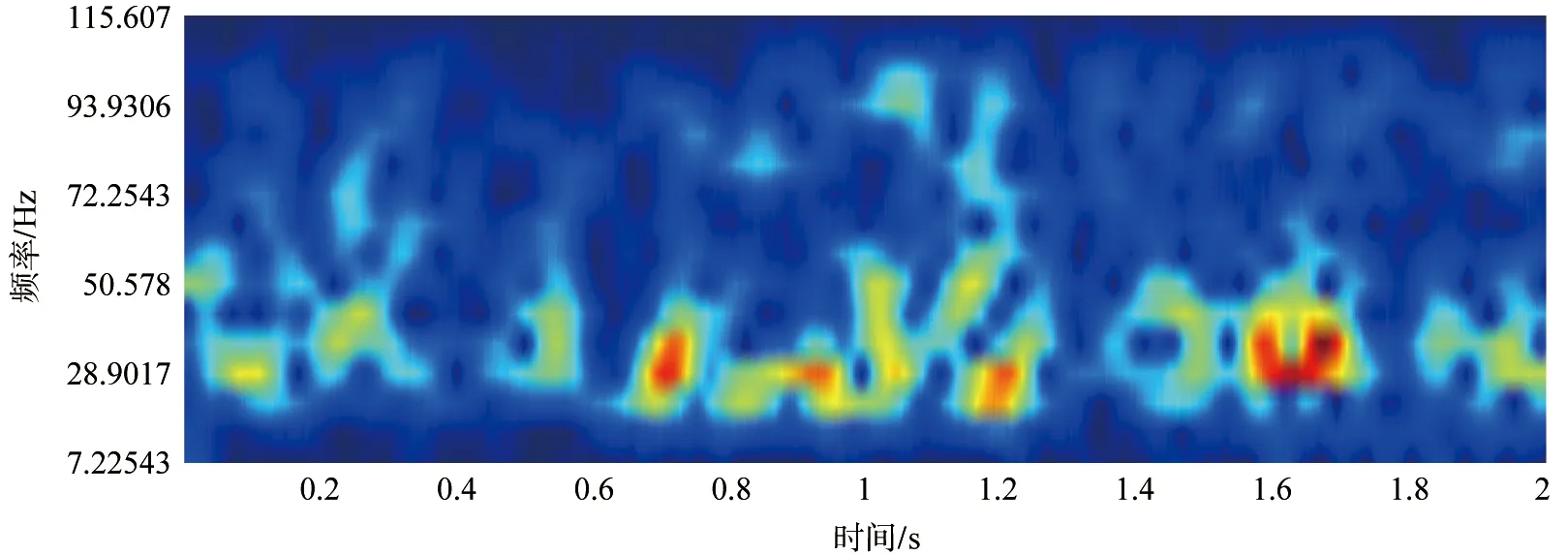
(a)stft时频图

(b)小波时频图

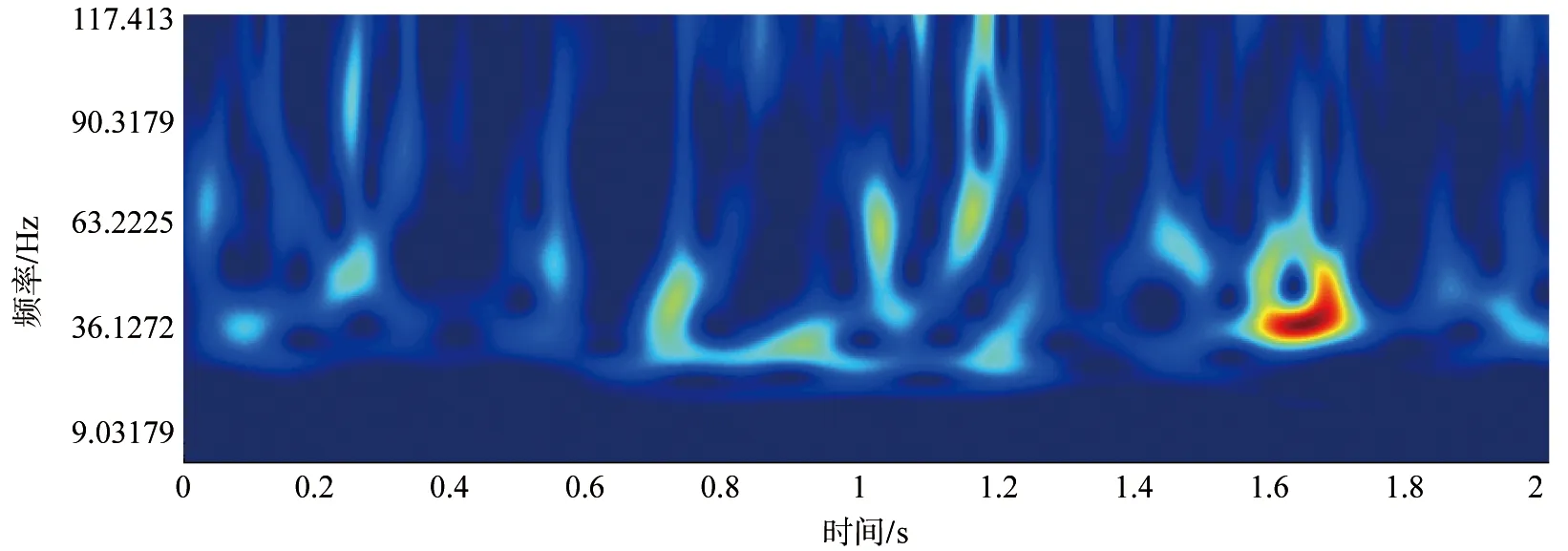
(c)S变换时频图

(d)MST时频图图6 实际地震记录时频谱Figure 6 Time-frequency spectrum of actual seismic record

4 结论

本文研究了修正S变换与常规时频方法在时频分析中的效果对比。修正S变换利用一个频率相关的一阶线性方程δ(f)代替S变换中的归一化高斯窗口的频率f，对传统S变换高斯窗函数相对固定的缺陷进行了修改。通过优化选取两个实数参数m、n的值，灵活地调控高斯窗函数宽度的变化速度。文中对雷克子波模拟信号、合成地震信号以及实际地震资料进行了多种时频分析，结果表明:相比较常规的时频分析方法，修正S变换能够对信号进行多分辨率分析，可以根据待分析信号的特点选择参数，具有更好的灵活性和更高的时频分辨率，改善了时频分布的聚集性，大大提高了地震信号时频谱的可读性和适应性，能更好地应用到不同需求的实际情况中。

[1]Boashash B,White L B. Instantaneous frequency estimation and automatic time-varying filtering [J]. Acoustics, Speech, and Signal Processing, 1990. ICASSP-90, 1990 International Conference on. IEEE, 1990: 1221-1224.

[2]刘葵, 刘招君. 时频分析在石油地球物理勘探中的应用[J]. 世界地质, 2000, 19(3): 282-285.

[3]刘喜武, 刘洪, 李幼铭, 等. 基于广义S变换研究地震地层特征[J]. 地球物理学进展, 2006, 21(2): 440-451.

[4]邓攻. S变换在地震时频分析中的对比研究[J]. 科技创新与生产力, 2011 (4): 73-76.

[5]黄忠来, 张建中. 同步挤压S变换[J]. 中国科学: 信息科学, 2016, 5: 007.

[6]Gabor D. Theory of Communication[J]. Journal of the IEEE.1946, 93:429-497.

[7]Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on signal processing, 1996, 44(4): 998-1001.

[8]Daubechies I. The wavelet transform, time-frequency localization and signal analysis[J]. IEEE Transactions on information theory, 1990, 36(5): 961-1005.

[9]Ville J. Théorie et applications de la notion de signal analytique[J]. Cables et transmission, 1948, 2(1): 61-74.

[10]胡明顺, 潘冬明, 徐红利, 等. 几种时频分析方法对比及在煤田地震勘探中的应用[J]. 物探与化探, 2009, 33(6): 691-695+ 709.

[11]Livanos G,Ranganathan N,Jiang J. Heart sound analysis using the S-transform [J]. IEEE Computers in Cardiology,2000,27:587-590.

[12]Mansinha L, Stockwell R G, Lowe R P. Pattern analysis with two-dimensional spectral localisation: Applicationsof two-dimensional S transforms[J]. Physica A: Statistical Mechanics and its Applications, 1997, 239(1): 286-295.

[13]崔伟雄, 李德春, 徐荣华. 煤田岩溶塌陷正演模拟及属性应用[J]. 物探与化探, 2011, 35(5): 648-651.

[14]张繁昌, 李灿灿, 徐旺林. 改进 Stockwell 变换法识别碳酸盐岩溶洞——以鄂尔多斯盆地奥陶系溶洞发育段为例[J]. 石油学报, 2015, 36(2): 182-187.

[15]刁瑞, 单联瑜, 尚新民, 等. 微地震监测数据时频域去噪方法[J]. 物探与化探, 2015, 39(1): 112-117.

[16]Mansinha L, Stockwell R G, Lowe R P, et al. Local S-spectrum analysis of 1-D and 2-D data[J]. Physics of the Earth and Planetary Interiors, 1997, 103(3): 329-336.

[17]Pinnegar C R, Mansinha L. Time-local spectral analysis for non-stationary time series: the S-transform for noisy signals[J]. Fluctuation and Noise Letters, 2003, 3(03): L357-L364.

[18]高静怀, 陈文超, 李幼铭, 等. 广义 S 变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532.

[19]陈学华, 贺振华, 黄德济. 基于广义 S 变换的信号提取与抑噪[J]. 成都理工大学学报 (自然科学版), 2006, 33(4): 331-335.

[20]Li D, Castagna J. Modified S-transform in time-frequency analysis of seismic data[C]//2013 SEG Annual Meeting. Society of Exploration Geophysicists, 2013.

[21]赵淑红,朱光明. S 变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4): 402-406.

[22]齐春艳, 李彦鹏, 彭继新, 等. 一种改进的广义 S 变换[J]. 石油地球物理勘探, 2010 (2): 215-218.

[23]陈学华, 贺振华. 改进的 S 变换及在地震信号处理中的应用[J]. 数据采集与处理, 2005, 20(4): 449-453.

Comparison of Modified S-transform (MST) and Traditional Time-Frequency Analysis Methods

Ruan Qingqing, Zhang Huixing, Wang Hao and Li Kairui

(Key Laboratory of Submarine Geosciences and Prospecting Techniques, Ministry of Education,Ocean University of China, Qingdao 266100)

Seismic signals are usually non-linear and non-stationary. The traditional Fourier transform based on stationary signal processing theory is difficult to depict frequency components at any moment. However, the time-frequency analysis technique has the capability of describing the partial features of signal both in time and frequency domains. The modified S-transform is a new method of time-frequency analysis, which was proposed due to the problems of the window function invariant and time-frequency resolution unadjustable in the S-transform. In this paper, we study and analyze the modified S-transform by comparing with the traditional time-frequency decomposition methods, such as short time Fourier transform (STFT), wavelet transform (WT) and S-transform. The time-frequency results of synthetic signals and field seismic data show that: the modified S transform has higher time and frequency resolution and better energy aggregation than the traditional time-frequency analysis methods. Therefore, it is more conducive to the processing of non-stationary signals.

time-frequency analysis; modified S-transform; S-transform; wavelet transform; short time Fourier transform

10.3969/j.issn.1674-1803.2017.04.14

1674-1803(2017)04-0066-07

国家科技重大专项(2016ZX05027-002)；国家自然科学基金(41204089)；大学生创新训练项目(201510423056X)。

阮清青(1991—)，男，中国海洋大学2014级硕士研究生，主要从事时频分析方法研究。

张会星，博士，副教授，Email:zhhuixing@sina.com

2017-03-10

文献标识码：A

责任编辑：孙常长