基于二次星座聚类提取信号特征参数的方法
2017-06-27单剑锋岳震林
单剑锋,岳震林
(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
基于二次星座聚类提取信号特征参数的方法
单剑锋,岳震林
(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
针对传统单一的聚类算法在低信噪比时对调制信号识别率低,以及进行特征提取的算法复杂并且难以实现的问题,为了提高星座调制信号在低信噪比的识别率,在对比了不同的MPSK和MQAM的星座图的差异性的基础上,提出了一种二次星座聚类提取信号特征值的方法。其利用改进核函数的DENCLUE(基于密度的聚类)提取信号星座图中密度最大点作为k均值聚类的初始聚类中心,并通过k均值聚类实现了一种新型的提取特征值方法,提取出一组特征值,采用支持向量机构造信号识别模型,并进行分类识别。仿真结果表明,所提出的方法相比传统单一的聚类算法,尤其是在低信噪比下对星座图调制信号的识别率和健壮性较好,并且基于该算法的实际系统简单可靠,具有广阔的发展空间。
星座调制;聚类算法;调制识别;特征提取
0 引 言
作为现代移动通信技术中的关键点—调制识别一直是通信领域的研究热点,特别进入21世纪以来,随着3G、4G通信的兴起,世界各个国家和地区的科学家、学者提出了很多调制识别通信信号方法[1]。近年来,MPSK和MQAM的研究发展日趋成熟,作为新兴的数字通信技术,其拥有频带利用率高、调制方式灵活、抗噪性能优越等众多优点[2]。未来将会在商用民用LTE通信、认知无线电、军用通信系统等领域内广泛使用[3]。然而,对MPSK和MQAM信号识别率的高低依然是目前能否进行实际使用的一个关键所在。因此,学者们对QAM调制信号的识别也进行了广泛而深入的研究[4-8]。例如,文献[9]使用减法聚类和粒子群结合提取星座图分类特征的方法,并使用函数进行判决分类。文献[10]基于遗传算法的自适应C均值聚类算法对MQAM进行星座识别。文献[11]使用模糊C均值聚类提取特征值,并使用神经网络进行机器学习和分类识别。然而上述文献只涉及了一种聚类识别方法,均值聚类法容易受初始聚类中心随机选取的影响,而陷入局部最优;DENCLUE(基于密度的聚类)必须选用样本中的点代替重构的星座图点,会导致聚类的结果不是最优;神经网络中也存在学习过程复杂缓慢等问题。
针对上述缺陷,提出了一种基于核函数估计的DENCLUE和k均值聚类的二次星座聚类算法,以提取QAM、PSK信号星座图中的特征值,并采用改进的支持向量机进行分类识别,提高了MPSK、MQAM等信号的调制识别率。
1 基于二次星座聚类提取调制信号特征参数的原理
对于某些基于星座图调制方式MPSK/MQAM的信号,采用基于二次星座聚类与支持向量机的新方法,实现对信号的调制识别,其识别系统模型如图1所示。

图1 识别系统模型
1.1 基于二次星座聚类的特征提取
DENCLUE是一种基于密度的快速独立的近似聚类方法[4]。k均值聚类是一种传统的基于距离的聚类算法[7]。针对MPSK/MQAM信号的调制识别领域,上述两种算法有明显的不足之处:DENCLUE计算后得到的聚类中心个数与初始给定半径ra影响较大,半径稍微增加就会导致密度的显著改变,不能准确还原星座图的真实图像(星座图可能存在变形、残缺),因此采用核函数估计方法,把每个测量对象都当作一个对周围区域的高密度指示器。k均值聚类中,聚类中心k的数目是事先给定的,但是在MQAM、MPSK信号的识别过程中,由于事先并不知道M是多少,无法给定聚类中心k的值,因此利用DENCLUE聚类算法给定一个初始的聚类中心,以提高k均值聚类的精度并且减少搜索聚类中心次数。在分析上述两种聚类算法的优缺点的基础上,将其结合并提出了一种二次星座聚类提取信号特征参数的方法:
(1)利用DENCLUE选择密度最大的k个初始聚类中心。
step1:对MPSK/MQAM信号进行信号预处理,得到信号具有n个点的星座图。定义星座图中样本点xi的密度指标为:
(1)
step2:利用式(1)计算每个点的密度指标,选择密度指标最高的样本点xc1作为第一个聚类中心,Dc1为其密度指标。其中,ra是一个正数,定义了该点的邻域半径,半径以外的数据点对该点的密度指标贡献较小,这里取:
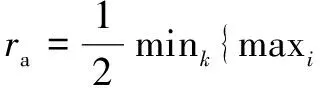
(2)
令xci为第i次选取的聚类中心,Dci为其密度指标,利用式(3)对其他数据点的密度指标进行修正。
(3)
其中,常数rb定义了一个密度指标显著减小的领域。通常设定rb大于ra,以避免出现太近的聚类中心对后续算法的干扰,这里取rb=1.4ra。
step3:在修正每个数据点的密度指标后,选定下一个聚类中心并不断重复上述过程,直至确定k个聚类中心。
(2)利用k均值聚类进行特征提取。
step1:对于上述给定的星座图,令J=1,并选择上面确定的k个初始聚类中心Zj(J),j=1,2,…,k;并计算星座图中每个点与聚类中心的欧氏距离D(xi,Zj(J)),i=1,2,…,n,j=1,2,…,k。
(4)
其中,Zx、Zy、xx、xy分别为聚类中心和星座图中其他点的横纵坐标。
如果欧氏距离满足式(5),则xi∈ωj。
D(xi,zj(J))=min{D(xi,zj(J))},j=1,2,…,k
(5)
step2:令J=J+1,计算k个新的聚类中心和误差平方和准则Jc的值:
(6)
并作以下判断:若Zj(J+1)不等于Zj(J),则J=J+1,并且重复进行该步骤。否则算法结束,得到k个聚类中心和每个聚类中心的类内点的集合。
step3:当聚类中心数目为k时,计算每个类内的点到该类中心点的欧氏距离之和s1,s2,…,sk,并求出距离之和的平均值Sk:
(7)
step4:对Sk进行归一化,定义单位欧氏距离的Sk为特征值Tc。
由于研究的是MPSK/MQAM信号的调制识别,所以聚类中心数k分别取2,4,8,16,32,64。即对接收到的信号点分别在以上6种不同的信号点进行上述二次星座聚类运算,并分别计算出不同k值的特征值Tk。在不同的信噪比下,针对不同的聚类中心k,分别计算出6种调制方式的特征参数T2、T4、T8、T16、T32、T64,如表1所示。

表1 特征参数
由表1可以看出,在一定的信噪比下,不同信号的六个特征参数有明显不同。因此,可以通过特征参数T2、T4、T8、T16、T32、T64来实现对BPSK,8PSK,4QAM,16QAM,32QAM,64QAM等6种信号的调制识别。
1.2 支持向量机的训练与调制识别
(1)支持向量机的训练。
由于提取的信号特征值较多,因此利用改进的一对一支持向量机方法来解决多种信号的分类问题,并使用多个二分类器共同组成MQAM/MPSK信号的分类器[12]。首先将上面经过二次星座聚类算法所提取的6个特征参数T2、T4、T8、T16、T32、T64送入支持向量机,对支持向量机进行机器学习,将出现最多的那个类别作为该样本最终的分类结果[13]。
(2)支持向量机的调制识别。
支持向量机训练完成后,将上述6种中的一种未知信号经过预处理后,利用上面的二次星座聚类进行特征提取,然后将6个特征参数T2、T4、T8、T16、T32、T64作为输入,送入训练好的支持向量机,输出得到测试信号的调制类型。
2 仿真结果与分析
使用Matlab 2014,Intel Core i5四核处理器进行仿真实验,选取的待检测信号分别是BPSK,8PSK,4QAM,16QAM,32QAM,64QAM,载波信号为正弦波,载波频率为2 000 Hz,采样频率为12 000 Hz,码元速率为500 bps,在信噪比为-2 dB,0 dB,2 dB,5 dB,10 dB时,对模糊C均值聚类算法和所提出的基于二次星座聚类进行信号特征提取的算法进行对比,均使用基于支持向量机的多分类器进行分类识别,每种情况各进行500次,计算出在不同信噪比下该方法对各种MQAM调制的平均识别率,结果如图2和图3所示。

图2 采用模糊C均值聚类算法进行特征提取的调制识别率仿真图
图2、图3表明,当信噪比为2 dB时,二次星座聚类算法对BPSK,8PSK,4QAM,16QAM的识别率基本接近100%,有了大幅提高,对32QAM的识别率达80%以上,对64QAM的识别率将近80%,高于基于模糊C均值聚类等单独的聚类算法;在信噪比为-2 dB时,对BPSK,8PSK,4QAM,16QAM的识别率高于90%,32QAM、64QAM也有70%左右,高于其他单一的聚类算法。充分体现了二次星座聚类算法在低信噪比下的健壮性,并且保持了较高的信号识别率。

图3 采用二次星座聚类算法进行特征提取的调制识别的仿真图
由于不同PSK/QAM信号的星座图的中心位置不同,导致当聚类中心为k时,其聚类中心位置不同,因此不同星座图各点到该点的聚类中心的距离不同,取平均并将其作为特征值,据此来判决不同的信号。当信号的星座图的中心位置差异越大时,该算法的正确率越高,并且在低信噪比下,通过两次星座聚类,可以有效去除噪声的影响,从而更加精确地获得星座图上信号的点,因此该算法在低信噪比下依然保持了良好的识别率。并且首先使用了DENCLUE算法找出了密度极大值点,在一定程度上给予了k均值聚类正确的初始聚类中心,避免了k均值聚类随机选取聚类中心不正确而导致多次计算选取,因此可以有效减少算法的迭代次数以及运算时间。
3 结束语
为了提高星座调制信号在低信噪比下的识别率,提出了基于二次星座聚类提取信号特征值的算法。选取了通信中几种常用的基于星座图的调制方式,利用二次星座聚类算法提取了具有明显差别的6种特征参数作为支持向量机的输入,并采用多个二分类器结合的支持向量机对其进行训练,以实现对MQAM、MPSK调制信号的调制识别。
基于Matlab的多次仿真结果表明,与传统单一的聚类算法相比,提出的识别方法在低信噪比下的抗噪声能力强,信号识别率较高,在实际的信号识别系统中具有一定的应用价值。
[1] 杨 杰,刘 珩,卜祥元,等.通信信号调制识别-原理与算法[M].北京:人民邮电出版社,2014.
[2] 党月芳,徐启建,张 杰.数字调制识别的关键技术与发展趋势[J].传感器与微系统,2012,31(10):1-5.
[3] 李苹苹,孙钢灿,申金媛,等.基于半监督聚类理论的MQAM信号的盲识别[J].青岛科技大学学报:自然科学版,2014,35(4):405-409.
[4] 杨发权,李 赞,罗中良.混合调制信号调制识别方法[J].中山大学学报:自然科学版,2014,53(1):42-46.
[5] 盛宇波,周 澜,程维文,等.Efficient entanglement purification in quantum repeaters[J].Chinese Physics B,2012,21(3):67-73.
[6] 王婷婷,龚晓峰.基于星座图的PSK、QAM信号联合识别算法应用[J].计算机应用研究,2015,32(7):2116-2118.
[7] Ericson K, Pallickara S. On the performance of high dimensional data clustering and classification algorithms[J].IEEE Communications Letters,2010,12(5):801-813.
[8] Ahmadi N,Berangi R.Modulation classification of QAM and PSK from their constellation using genetic algorithm and hierarchical clustering[C]//ICITA.Cairns:IEEE,2008:98-103.
[9] Li Yanling, Li Bingbing, Yin Changyi.Modulation classification of MQAM signals using particle swarm optimization and subtractive clustering[C]//IEEE 10th international conference on signal processing.[s.l.]:IEEE,2010.
[10] 吴月娴,葛临东,许志勇,等.基于遗传算法的自适应聚类与MQAM星座识别[J].计算机工程,2007,33(22):39-41.
[11] Yang Faquan,Li Zan.Method of neural network modulation recognition based on clustering and Polak-Ribiere algorithm[J].Journal of Systems Engineering and Electronics,2014,25(5):742-747.
[12] 程 佳.支持向量机与K-均值聚类融合算法研究[D].大连:辽宁师范大学,2008.
[13] Zhu Zhechen,Aslam M W,Nandi A K.Support vector machine assisted genetic programming for MQAM classification[C]//10th international symposium on signals,circuits and systems.[s.l.]:[s.n.],2011.
A Method of Extracting Feature Parameters of Signals Based on Two Constellation Clustering
SHAN Jian-feng,YUE Zhen-lin
(School of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
Aimed at the problems that traditional single clustering algorithm has the low recognition rate of the modulation signal in low SNR (Signal-Noise Ratio) and feature extraction algorithm is complex and difficult to achieve,in order to improve the recognition rate of the constellation modulation signal in low SNR,an innovative method for twice constellations clustering has been proposed based on the comparison of the differences of MPSK and MQAM constellation diagram,where improved kernel function DENCLUE (density-based clustering) is used to extract the maximum density of the signal constellation as the initial clustering center ofK-means clustering.The new feature value extraction method has been implemented for acquisition of characteristic values.The support vector machine has been used to construct the signal recognition model and its classification and identification has been conducted.Simulation results show that the method is better than traditional single clustering algorithm,which is good at the recognition rate and robustness of constellation modulation signal in low SNR especially and that the practical system with this proposed algorithm is simple and reliable with broad development space in future.
constellation modulation;clustering algorithm;modulation recognition;feature extraction
2016-06-19
2016-09-22 网络出版时间:2017-03-13
国家自然科学基金面上项目(GZ212015)
单剑锋(1967-),男,副教授,研究方向为电路与系统、智能信息处理、电路故障诊断;岳震林(1992-),男,硕士研究生,研究方向为智能信息处理。
http://kns.cnki.net/kcms/detail/61.1450.tp.20170313.1546.058.html
TP911
A
1673-629X(2017)06-0091-04
10.3969/j.issn.1673-629X.2017.06.019
