考虑孔隙变化影响的土体压缩特性试验研究

王兴陈

摘要：为实现不同扰动条件下原位土压缩特性的模拟，文章基于结构性破损压缩模型，提出孔隙相对变化指数E，研究土体孔隙变化压缩特性的影响，通过对不同扰动状态下的原状软土进行固结试验，分别建立E_v与土体结构屈服应力及结构破损指数6的相关关系，从而提出基于室内压缩试验结果预测原位压缩特性的方法。结合相关试验数据的分析，验证了该方法的可行性。

关键词：结构性软土；孔隙相对变化指数；压缩特性；结构屈服应力；结构性破损指数

原状土的压缩特性并不能准确反映在室内土体压缩试验中，但可以通过室内试验进行预测。刘维正等选用结构屈服应力和结构破损指数6表征土体压缩性状；S.Horpibulsuk等、T.S.Nagaraj等研究结构屈服应力sy与原位不排水强度su的相关关系，提出原位压缩曲线的预测方法。前人仅建立扰动指标与土体屈服应力的相关关系。事实上，扰动状态下，物性变化不仅影响结构屈服应力，还与结构破损有关，要研究通过室内试验预测原位土体压缩性状的方法，必然要考虑物性变化对土体结构屈服应力的变化，以及结构破损的演化规律。

本文提出物性变化参数：孔隙相对变化指数E_v，研究其对土体压缩性状的影响，建立其与土体结构屈服应力及结构破损指数b的对应关系，进而提出通过室内压缩试验预测原位压缩特性的新方法。

1.原状土的压缩特性

原状土的压缩特性关系如图1所示。重塑土的压缩曲线（e-log）是一条直线，原状土的压缩曲线分为三个阶段。平缓阶段：当压力小于结构屈服应力时，曲线近似是一条直线，e=eo；陡降阶段：当大于时，土的结构破坏，孔隙比减小；趋同阶段：当压力继续增大到某一特征值时，重塑土和原状土的孔隙比差值将趋于常数，为土结构引起的剩余孔隙比evsr。

由图1可知，原状土的孔隙比可以下式表示：

e=e_R+e_s（1）

式中，e是原状土的孔隙比，e_r是相同压力下重塑土的孔隙比，e_s是土结构性引起的额外孔隙比。

Liu，Carter等人对不同软土进行研究，发现当>时，土体结构引起的额外孔隙比es与（）b成反比，其中b为结构破损指数，描述结构性对孔隙比的影响程度，取值由土的种类和状态决定。

图1可知，垂直应力远超过屈服应力，软土依然存在剩余孔隙比e_sr，可以发现额外孔隙比e_s将满足下式：

es=esy（/）b+esr（2）

其中，esy是对应于屈服应力时的额外孔隙比。

Horpibulsuk等提出曼谷原状土压缩曲线表达式如下：

<时，e=e_o （3）

>时，e=eR+esy（/）b+esr （4）

>>时，e=e_r+e_sr （5）

当压力=时，上式满足：

e=e_ry+e_sy+e_sr

（6）

其中，Horpibulsuk通过实验得出曼谷土结构破损指数b=1，而原位屈服应力syf由下式确定：

=3.78S.+7 （7）

S_u为现场十字板不排水强度，单位为kPa。

2.孔隙相对变化指数E_v

本文借鉴Z.Hong等对扰动度定义的思路，提出孔隙相对变化指数E_v，定义如下式所示：

Ev=x100% （8）

式中，表示有效上覆應力为时扰动土的孔隙比，evr表示有效上覆应力为时重塑土的孔隙比。如图2所示。

由式（8）可知，土体原位完整状态时，esvO基本与eO相同，此时，Ev=0；而当原位完整状态趋于重塑状态时，基本与evr相同，此时，Ev=1。

参数的各个指标可由原状土和重塑土的压缩曲线求得。

3.试验过程及结果分析

土样物理力学指标如表1所示。

3.1不同初始振动的固结试验

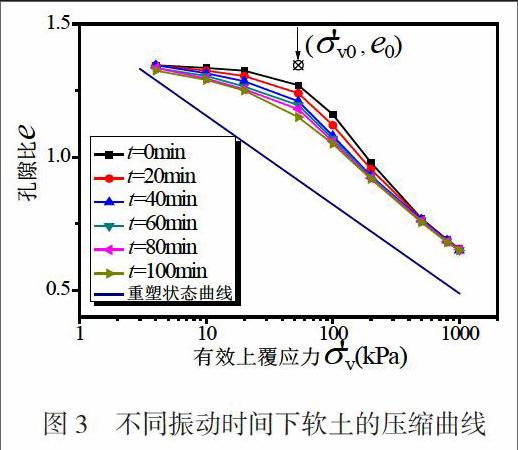
通过振动试验模拟不同扰动条件对土体压缩特性的影响。进行6组时长为0，20，40，60，80，100min的振动试验。振动结束后立即取样进行固结试验。试验结果如图3所示：

3.2试验结果分析

图3中可以发现，振动时间变长，相同竖向应力状态下土体的孔隙比不断变小。

由式（8）可计算出不同振动时间下孔隙相对变化指数大小，其关系如图4所示。

由式（12）可知，随着Ev增加，对应的结构破损指数线性减小，因此，建议由下式确定原位土体结构破损指数：

（13）

式中，为原位土体结构破损指数，为重塑土体结构破损指数。

根据结构破损指数的定义，重塑土体结构破损指数趋向于零，如图5所示。

则式（13）可转化为：

（14）

4.原位压缩曲线的预测方法

本文基于Horpibulsuk等曼谷粘土压缩曲线预测方法，提出通过室内压缩试验预测原状土压缩曲线的新方法：

（1）试验测出重塑土压缩曲线、e_o及，并用e_o画出平缓阶段的压缩曲线；

（2）实验得出任一扰动条件下的压缩曲线，确定对应的及b，由式（8）计算出，由式（11）、式（14）分别计算出对应原状土的及bf。

（3）取=1000kPa时对应的孔隙比差值为esr。过屈服应力点（，eO）及特征点（）画曲线eS=esy（/）bf+esr。

（4）>>时，e=eR+esr

5.试验分析与验证

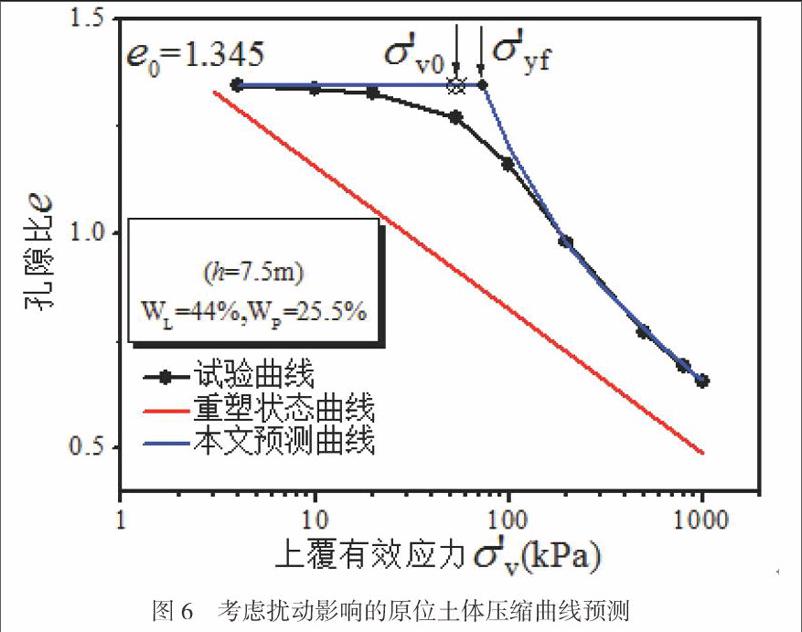
选取t=0min的室内土样验证预测。首先确定出原位状态e0=1.345，=53.5kPa，=68.3kPa，根据式（4）计算室内扰动土结构破损指数b=1.11，根据式（8）计算此扰动条件下Ev=7.5%，并由式（11）和式（14）分别计算出原状土原位状态下=73.8kPa，bf=1.2，即可预测出原位土压缩曲线，如图6所示。

6.结语

借鉴Hong扰动度定义的思路，提出孔隙相对变化指数，研究其与土体屈服应力、结构破损指数的相关关系。提出确定原位土体压缩特性的新方法，扩展了Horpibulsuk方法的应用范围，实现对不同扰动条件下原位土体压缩特性预测。