轮轨接触磨损与裂纹产生机制的有限元模拟

李国斌，邝卫华（广州番禺职业技术学院机电工程学院，广东广州 511483）

轮轨接触磨损与裂纹产生机制的有限元模拟

李国斌，邝卫华
（广州番禺职业技术学院机电工程学院，广东广州 511483）

为探究轮轨接触磨损与裂纹产生的机制，利用滚动、滑动轮轨接触对变形表面进行金相研究。其次，提出一种可以模拟滚动、滑动接触表面附近的变形过程的多尺度有限元模型。此外，现实中滚动滑动轮沿轨道的蠕滑行为是被广泛认可的。关于这些轮轨接触的实际形变量的从微米到毫米范围内的塑性剪应力可以预测。使用多尺度模型得到的数值结果可以比较金相观察，结果与实际相符合，具有一定的现实指导意义。

轮轨磨损；裂纹；金相观察；有限元模拟

铁路系统钢轨磨损和裂纹形成机理的研究包含许多相互联系的方面。本文主要是通过金相观测和数值模拟来研究轮轨的磨损开裂机理。

在滑动轮轨接触，由于面与面的接触距离，所以在几乎所有情况下，接触面都会产生塑性形变。变形层的厚度，变形量及其分布取决于材料的轮轨和表面粗糙度。虽然，这一过程可以用塑性变形中的粗糙表面接触力学来描述，但是，目前还没有分析方法可以解决和描述循环接触多粗糙，也没法解决材料的塑性加载的问题描述［1～3］。

为计算粗糙的滑动接触，增加了微凹凸体几何模型。同时计算开发允许使用复杂的材料模型描述的弹性－塑性材料的行为在多尺度有限元模型。在这种方式中，可以更准确地提出变形过程中的接触区。虽然，有研究表示两个粗糙表面之间的接触以不同的方式来展现。多位研究人员对于单凹凸接触处理的接触压力分布和破坏行为进行了大量的研究。通过调研粗糙表面和纯弹性材料的接触压力和应力分布可以发现，粗糙表面或凹凸模型使用弹性－塑性材料的行为可以在纯正常载荷下进行说明［4～6］。但是，没有处理的蠕滑接触的详细描述。

本文主要研究内容为，在轮轨试验台上进行滚动滑动接触的表面变形试验，结果表明，磨粒产生和裂纹萌生之间几乎没有区别，同时，将数值模拟的结果、变形量、变形分布于金相图像相对比，以验证模拟方案的可行性。

1 表面变形

表面磨损和表面裂纹的研究表明，车轮／钢轨接触裂纹的萌生总是与一些车轮通道表面的严重变形有关［7］。从金相图像中总结裂纹的萌生过程，有必要了解真实的接触情况。事实上，真实的表面总是粗糙的。从接触力学的角度描述严重变形的表面层在车轮和钢轨的变形和深度量对应的凹凸的大小和长度［8～11］。

沿导轨的运行面存在不同方向的横向滑动与正常的负载作用。因此，在运行面不同的横向位置上，表面的变形是不同的。如图1所示，轨面显示用80 000轮加载通过在轮轨试验台200 kN和横向载荷40 kN正常负载。轨道材料R260，没有迎角和纵向牵引的应用。图1所研究的表面位于轨道的轨距角附近。

使用聚焦离子束（FIB）切割到几个运行表面位置的深度，如图2、图3所示，这些调查发现两个典型的变形类型。一种变形在深度小于10μm的表面上表现出长的平行裂纹，在下面称为“片状结构”。变形的其它类型，在下面的“片状结构”，显示了一个角对表面和变形后线向下增长将达到10μm以上深度。由于这些FIB切割没有系统地选择沿表面，它是不可能相关的表面负载在所观察到的轨道位置完全与所观察到的表面变形。对于这种相关性，本文将提供一种更系统的方法。根据牵引力和正常负载的轮轨接触的表面变形，可判定方法的可行性与系统性。

图1 变形表面附近的铁路轨距角80 000个周期后的裂缝和磨损颗粒

图2 在另一个表面位置上的深度轨道上的切口示出下面的表面层状结构

图3 切割到深度以下的表面下面检测到片状结构

从一方面看，在裂纹的片状结构有从表面到深部的发展趋势，并且，产生的分层和磨损合理是可以预测的。而且，片状表面变形与片状变形的区别是研究的一个重要方面。可以认为材料轨道表面位置不同的以及负载类型确定的表面变形都有作为后果的表面裂纹的类型的意义。为了证明这个假设的力学模型，进行了多尺度有限元模型的开发。模拟车轮滚动滑动行为，包括“粗糙度效应”。

2 形变模型

轮轨接触表面磨损及表面裂纹萌生的研究需要了解实际接触情况。车轮和钢轨之间的接触参考库仑摩擦定律，选取摩擦系数为0.5。图4显示了二维多尺度模型的三倍缩放细节的网格附近的粗糙建模表面。如表1所知，6种回应力的塑性材料模型描述的运动强化轨道材料行为。Ci值表示切线模量，Di值对应指数。材料的初始屈服应力R260设定为320 MPa。在表1中给出所用的材料模型的参数拟合对R260型钢轨钢的试验。车轮和钢轨的杨氏模量为206 GPa，泊松比为0.28。

表1 钢轨材料模型的6种回应力表述

3 多尺度有限元模型

新的两维（2D）多尺度模型的轮／轨接触的平面应变包括粗糙的凹凸接触和粘滑现象的实际接触情况。当三维（3D）的接触情况被转移到2D，被认为是对弹性材料的行为进行了改造，类似于弹性－塑性材料的行为。主要的问题是，从三维到二维的转换，对厚度的依赖性是一个在线的类型的接触，可以接触线（2D）或圆形（3D）。这种效应无法在现有的模拟条件下得到满足，但必须考虑二维模拟结果之间的比较和实际接触的情况。

从接触压力分布的三维模型中的接触点的某些方向可以被选择当成一个二维模型用来计算在该方向加载。如图5所示，为了使弹性接触点的2D模型更加贴合实际，特引入赫兹公式，那么2D接触片的长度a2D和在二维接触点P0.2D最大接触压力计算F的力如下所示：

式中：E代表杨氏模量，v代表泊松比。这个公式的参数F和R的二维模型可以从接触贴片长度a3D和三维模型的最大接触压力P0.3D计算：

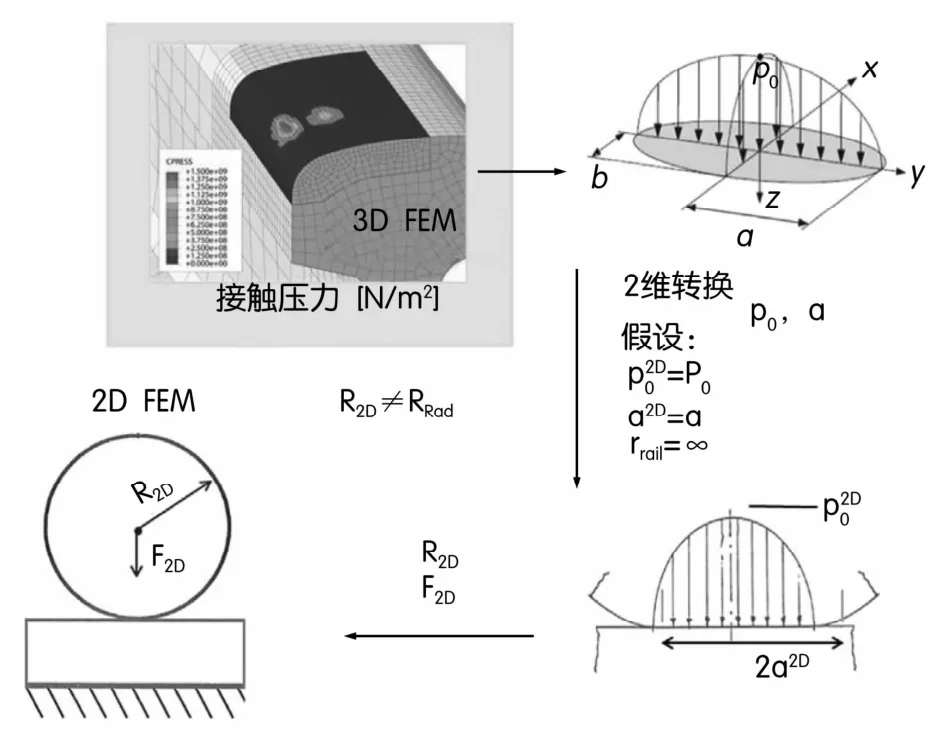
图5 触电负载变换示意图

粘滑运动的车轮轮轨道运动模型被认为是主要的车沿轨道运动模型。此外，粗糙接触模型需要适当参考钢轨材料或车轮材料的特点。一个完全真实的描述材料大概需要剪棘轮试验和循环高压扭转试验；试验费时费力且收效甚微。但是，模拟所需要的材料模型及参数恰恰是由这些试验所得到的。

建模测得的表面粗糙度集中于车轮部分的中间以及在轨道部分的中间，其余表面保持平坦。为展示粗糙度对其微观尺度的影响，粗糙区域内的元素的长度设置为5mm。同时，使用平面厚度为1 mm的线性平面应变单元。车轮部分的元素数量为8 761，在轨道部分为9 671。

通过模拟只有1 mm的粗糙表面的模型可以达到减少计算时间的目的。通过计算一个14 mm长的部分模型的粗糙表面的模拟结果与1 mm粗糙模型表面模拟结果大致相同。在建模的粗糙表面，平面的接触可以假定不改变整体粘滑、自由滚动或滑动行为。在光滑，小粗糙和长粗糙模型之间的接触压力分布的差异如图6所示。

图6 轮轨接触下的不同表面光滑程度的触应力和应变计算模型示意图

导轨的底部固定在正方向，两侧固定在纵向。试验铁轨长81 mm，高40 mm，车轮的截面为圆形，楔形角度为125°，这可以看成一个以中心点为中心移动的刚性契合，在该参考点，车轮的负载和位移可以被控制，在垂直方向上，施加负载fN。车轮的滚动滑动运动是通过一个切向力fT来实现的，其中T＝FT／FN。当没有完整的滑移时，轧制过程是准静态模拟。时间增量长度定义，车轮的旋转位移小于滚动方向的一个接触元件的长度。轧制开始后需要一定的距离，才能使接触平衡，模型变形和边界条件达到稳定滚动滑动状态。这个滚动距离取决于负载、摩擦条件、模型的大小和边界条件。可以改变有限元模型中一个接触点的长度，直到100 mm或直至一个更大的模型。在全尺寸的轮轨试验中，需要几百毫米才能达到稳定的滚动滑动状态。试验模型中，车轮滚动超过17 mm的距离之前到达粗糙的建模表面。

4 试验结果

4.1 依赖数量的负载周期性在线

模拟的负载情况应代表滚动和部分滑动加速轮。因此，虚拟转速规定的纵向力相反的滚动方向作用于车轮中心。车轮部件的正常装载量为10 kN，与轧制方向相反的力为3 kN，导致牵引值为0.3。依据设定，一个平面外的厚度为10 mm的模型，加载的10 kN对应于真实情况下，约为80 kN的车轮负载。由图6可知，由此产生的接触压力和剪切应力在钢轨表面形成一个表面大部分光滑，部分粗糙且粗糙表面Rmax＝11.4μm，测得的粗糙度曲线代表了磨损钢轨的一个典型参数。在光滑表面模型的正常负载产生的最大接触压力为1 000 MPa。使用此负荷的车轮的滚动状态是部分滑移。

车轮的粗糙度的最大值Rmax＝2.4μm，模型是车轮在粗糙的钢轨表面上滚动。在整个车轮通道中，整个接触片移动在这个粗糙的区域，并根据现实的粗糙接触的情况下产生的压力和剪切应力分布。接触压力和剪切应力峰值高度依赖于两个接触面的微观接触。这些应力峰是极端的塑性变形的表面附近可见和可测量的金相调查。

由图7可知，至少在表面上，沿路径的深度塑性变形的最大深度依赖于所选择的位置的粗糙程度。由图8可知，当车轮进入中等粗糙程度的轨道时的等效塑性剪切应力会随时间变化，得到在轨道表面，对于所使用的粗糙材料的塑性剪切应变达到的最高值。由上图可得，塑性形变主要取决于粗糙接触以及0.1mm范围内深度的影响。同时塑性形变的发展有着几个较为明显的周期，同时，都在最后阶段趋于稳定。对于所使用的粗糙度曲线，牵引值，正常负载和所选择的材料参数，最大等效塑性应变达到190%以上后，可能会不断增加。

图7 钢轨表面到深度的路径累积的等效塑性应变示意图

图8 五种不同钢轨深度下轧制周期位移增量

4.2 结果比较与讨论

模拟结果与金相调查的表面变形的比较，如图9所示，可以发现塑性剪切变形的位移有限元网格显示50个周期。通过判定最后一个周期的的恒定位移增量，进而推广到200个周期。图8实现了这些增量计算的50个周期。在第五个负载循环中达到最高增量。经过50个周期的位移增量趋于一个恒定值。接下来，这个常数值将用于外推到200个负载周期。可以预计，经过几百个周期已经稳定状态并趋向于一个恒定的变形增量。

图9中黑色实线是计算结果，黑色虚线为外推位移。位移图的背景是一个纵向的横截面的轨道加载约100个周期具有相同的负载条件下的模拟金相图。尽管不同的循环次数之间的金相调查和模拟可以看出，深度的位移分布的横截面的可见变形相对明显。同时比较金相图片可以得出，之后几百个周期轨道的变形状态趋于平稳，且不会发展更多的形变。

图9 不同周期内柜面位移计算示意图

图9是由车轮通过的次数而非变化层的深度来解释的。同时，层的深度将取决于所施加的表面牵引力变化的凹凸形状和材料。然而，假设的剪切变形的量，深度和分布是直接确定磨损和裂纹萌生过程。此外，裂纹路径的短表面裂纹似乎总是遵循材料变形路径。改进的钢轨表面定量计算不仅有助于了解表面形变，以及钢轨表面颗粒的产生、裂纹萌生和早期裂纹扩展的机制，同时也是预测这些发展的工具。

5 结 论

1.提出一种新的二维平面应变粗轮轨接触模型，其中包括粘滑现象的现实接触情况，并以机械的方式与三维情境相关。金相观察表明，由于粗糙接触造成的极端变形会产生磨损颗粒和裂纹贯穿钢轨的运行表面。开发的模拟证明，对应金相观察，一定周期后靠近钢轨表面的一个高度塑化层产生，并与金相调查结果做了比较。

2.粗糙表面的可见变形与裂纹萌生和磨损有关。变形的角度对裂隙的产生及磨损颗粒的发展有一定的影响。

3.裂隙的增长不是必然的，裂纹的进一步增长取决于变形量。

4.适当的表面变形定量描述，可以解释和预测金相观察过程中的剥落、磨损颗粒分层、粗糙下的表面裂纹萌生或粗糙下的内部裂纹萌生。

［1］ 孙琼，李国顺，臧其吉.表面粗糙度对轮轨接触的影响［J］.中国铁道科学，1996，（4）：40－47.

［2］ 郭静，王文健，刘启跃，等.不同工况下轮轨材料间的摩擦磨损行为［J］.机械工程材料，2013，（1）：43－46.

［3］ 常崇义.有限元轮轨滚动接触理论及其应用研究［D］.北京：中国铁道科学研究院，2010.

［4］ 车鸿博.轮轨滚动接触疲劳裂纹萌生及扩展分析研究［D］.兰州：兰州交通大学，2014.

［5］ 张军.基于有限元法的轮轨蠕滑理论研究［D］.大连：大连理工大学，2003.

［6］ 张澎湃，井秀海.轮轨接触应力的有限元计算［J］.铁道车辆，2007，（6）：4－8＋47.

［7］ 徐新玉.城市轨道交通轮轨异常磨损原因分析与改进措施［J］.机车车辆工艺，2010，（5）：43－44.

［8］ 侯传伦，翟婉明，邓锐.曲线磨耗状态下轮轨弹塑性接触有限元分析［J］.中国铁道科学，2009，（5）：28－33.

［9］ 刘玮.高速铁路桥上有砟轨道力学特性及结构选型研究［D］.北京：北京交通大学，2009.

［10］吴兵.高速轮轨黏着特性数值与实验研究［D］.成都：西南交通大学，2015.

［11］蔡宝春，蒋华臻，王文中，等.轮轨试样表面粗糙度取向对油润滑下摩擦系数的影响［J］.力学学报，2016，（5）：1 114－1 125.

The W heel Rail Contact W ear M echanism and Finite Element Simulation of Crack

LIGuobing，KUANGWeihua
（Mechanical and Electrical Engineering Institute，Guangzhou Panyu Polytechnic，Guangzhou 511483，China）

In order to investigate themechanism ofwheel rail contactwear and crack formation，the rolling and sliding wheel rail contact.Secondly，amulti－scale finite elementmodel is proposed to simulate the deformation process of rolling and sliding contact surfaces.In addition，it iswidely accepted that the creep behavior of the rollingwheel along the track.The plastic shear stresses of the actual shape variables of the wheel rail contact can be predicted from micron to millimeter.The numerical results obtained by the multi－scale model can be compared with the metallographic observation，and the results are consistent with the actual situation，which has a certain practical guidance significance.

railwear；crack；metallographic observation；finite element simulation

TG113.22

A

1003－5540（2017）03－0056－05

2017－04－28

广州市教育科学规划课题（1201532993）

李国斌（1962－），男，副教授，主要从事机构及机械基础课程的教学与研究工作。