AI算法可预测材料特性，未来建筑业或被颠覆？

□编译/李耀琪

AI算法可预测材料特性，未来建筑业或被颠覆？

□编译/李耀琪

算法，是人工智能（AI）如何实现应用的解决方法。用最优的算法快速地解决问题一直是前沿研究的重点内容。就目前而言，虽然AI技术更多地应用到例如智能识别、VR/AR、机器人、智能家居等领域，但是这并不代表在传统领域就无法得到应用。研究人员Jones和McCarthy就通过支持向量机算法（SVM）对混凝土强度随着时间的变化进行了预测，而且预测结果与实际结果相似度极高。该项研究也预示着AI应用正在由高端科技向传统领域进行过渡与渗透。

众所周知，混凝土是一种建材领域特定的、必不可少的基础材料，它能够在浇筑后的很长时间内获得一定的强度，从而保持物体在特定应用下的稳定性。根据人类的长期应用经验，在一般情况下，普通混凝土是指已经老化28天，具有抗压强度的样品。这样的混凝土能够广泛应用到许多建筑领域。因此，强度成为混凝土在特定应用环境下的重要标准。

事实证明，对混凝土强度的快速和可靠的预测对提高经济效益具有重要的意义。现在，混凝土强度的快速预测已经成为了研究的热门领域，并且已经开展了大量的实际研究工作。研究人员发现，通过AI的两项技术可以提出一个能够精度预测混凝土压缩强度的模型，而这两项分别是具有变革性的支持向量机（SVM）和多变量非线性回归。

在早期的时候，就有研究者提出用支持向量机来研究预测混凝土的抗压强度。预测模型中使用的变量来自于混合比例元素和7天抗压强度的知识中。这些模型能够良好地预测混凝土的抗压强度，并且在研究中使用的数据能够与非线性多变量回归产生良好的相关性。此外，SVM模型被证明是，具有最小误差和标准偏差的轻质泡沫混凝土抗压强度重要的预测工具。

介绍

混凝土被认为是世界上最重要的建筑材料，也是用于建筑或土木工程结构的最常见的材料。目前，建筑业对于使用轻质泡沫混凝土（LFC）作为建筑材料表现出了极大的兴趣，因为它具有许多有利的特性，例如更轻的重量，易于制造，耐久性和低成本效益。

泡沫混凝土是新一代轻质混凝土，具有一些有吸引力的特性，如流动性、自压实性和自流平性，低尺寸变化和超低密度。此外，该材料可以设计成具有可控制的低强度，优良的绝热性能和良好的承载能力等特性，并且取材非常容易。

由于其独特的性能，泡沫混凝土具有用于建筑工业中各种应用的潜力。研究人员Jones和McCarthy就对泡沫混凝土用作结构材料的潜力进行了调研。他们对构成材料和混合比例对泡沫混凝土的性能和行为产生的影响进行了分析，包括泡沫混凝土的抗压密度、水泥类型和含量、水/水泥比例、表面活性剂类型和固化方式等。结果发现，由于泡沫混凝土具有优良的隔热性和轻量性，所以，它可以补充其他材料来用于更高强度的结构应用。

混凝土强度预测方法

一直以来，人们对于普通水泥浆、砂浆和混凝土，已经有了几种强度预测方法。然而，在当前更快的施工速度下，需要生产更多的混凝土，而且要保证所生产的混凝土质量与标准和规格的一致性。

因此，旧方法就无法满足新需求下的生产效率了。现在，人们已经通过计算建模、统计技术等新的AI手段来改进与测试混凝土硬度的检验方法。

统计技术：一些研究工作集中在使用多变量回归模型来提高预测的准确性。统计模型具有吸引力，一旦拟合，它们可以用于比其他建模技术更快地执行预测，并且相应地更容易在软件中实现。统计分析还可以通过相关分析提供影响28天抗压强度的关键因素。由于这些原因，选择统计分析作为本研究的强度预测技术。

实验准备材料与要求

轻质泡沫混凝土的制造由四种类型的材料组成，即普通波特兰水泥、砂、水和泡沫。

生产轻质泡沫混凝土的材料：1.符合I型波特兰水泥要求的普通波特兰水泥（OPC）是符合英国标准（BS EN 197-1：2000）规定的要求的；2.不同尺寸的细硅砂（600μm，1.18和2mm）；3.正常的自来水；4.稳定的气泡（在泡沫发生器中混合发泡剂和水而产生。目的是通过将预制的稳定泡沫结合到新鲜的轻质泡沫混凝土中来控制轻质泡沫混凝土的密度。）。

对于该研究，发泡剂与水的比率为1∶30体积比。使用的超增塑剂是符合ASTM标准规格（ASTM C494M-04）的GLENIUM52。超增塑剂有深棕色水溶液。基于轻质泡沫混凝土的目标密度w / c和s / c（砂与水泥比）设计最佳混合比例。密度范围为15001750和1800kg / m³。所使用的w / c比的范围为0.5、0.45、0.4、0.35和0.3，而对于本工作中的所有混合物，s / c为1.0。本研究中使用的固化方法是密封固化。制备泡沫混凝土，然后倒入立方体中。在7天和28天的时候，分别测试150套混凝土立方体的密度和抗压强度。

预测算法

支持向量机（SVM）

支持向量机（SVM）是用于分类或回归的强大的监督学习算法。SVM是一个有区别的分类器，也就是说，它们在数据簇之间画一个边界。支持向量机是基于定义决策边界的决策平面的概念。决策平面是对具有不同类成员的一组对象进行分离的方法。支持向量机（SVM）主要是通过在分离不同类标签的多维空间中构造超平面来执行分类任务的分类方法。SVM支持回归和分类任务，可以处理多个连续和分类变量。为分类变量创建一个虚拟变量，其中实例值为0或1。因此，三个层次（A，B，C）组成的分类因变量则由一组虚拟变量来表示：

A：{1 0 0}，B：{0 1 0}，C：{0 0 1}

为了构建最佳超平面，SVM则采用迭代训练算法，来将函数误差降到最小。根据误差函数的形式，SVM模型可以分为四个不同的组：

·分类SVM类型1（也称为C-SVM分类）

·分类SVM类型2（也称为nu-SVM分类）

·回归SVM类型1（也称为ε-SVM回归）

·回归SVM类型2（也称为nu-SVM回归）

回归SVM

在回归SVM中，必须估计因变量y对一组独立变量x的函数依赖性。与其他回归问题一样，它假定独立变量和因变量之间的关系是由确定性函数f加上一些添加剂噪声：

y = f（x）+噪声

然后，任务是找到用于f的函数形式，其可以正确地预测先前没有呈现SVM的新情况。这可以通过在样本集上训练SVM模型来实现，即训练集，涉及类似分类的过程以及误差函数和顺序优化。根据该误差函数的定义，可以识别两种类型的SVM模型。

回归SVM类型1

对于这种类型的SVM，误差函数是：

误差函数最小化受制于：

支持向量机模型中可以使用几个内核。

这些包括线性、多项式、径向基函数（RBF）和Sigmoid函数。

内核函数

其中K（Xi，Xj）=φ（Xi）·φ（Xj）

也就是说，核函数表示通过变换φ映射到高维特征空间中的输入数据点的点积。γ是某些核函数的可调参数。RBF是目前支持向量机中使用的最受欢迎的内核类型选择。这主要是因为它们在实际x轴的整个范围上的局部和有限响应。

径向基函数（RBF）

这是一个实数值函数，其值仅取决于离原点的距离，因此可以得出φ（X）=φ（‖X‖）；或者取决于到被称为中心的某个c点的距离，使得φ（X，C）=φ（‖X-C‖）。我们把满足φ（X）=φ（‖X‖）的任何函数都称为径向函数，并规定通常为欧几里德距离。当然，其他距离函数也是可行的。例如，对一些径向函数来说，使用Lukaszyk-Karmowski度量可以避免由于所确定的系数wi导致矩阵恶化的问题，因为‖X‖总是大于零的。

径向基函数的总和通常用于近似估计给定函数。这个近似处理的过程也可以被解读为一种简单的网络。Preetham等人于2014就已经提出了与土木工程相关的支持向量力学方法（SVM）问题的现状。目前，许多领域正在进行SVM技术的数值研究，同时，许多RBF的研究也被用作支持向量分类的内核。

预测结果

轻质泡沫混凝土的性能

这项工作主要是对第7天和第28天两个时间节点，轻质泡沫混凝土样品的参数进行测试，包括混凝土样品的新鲜度、密度、抗压硬度。根据早期的研究结果显示，不同的混合比例会造成样品密度的差异，而密度被认为是影响混凝土硬度的关键因素。因此，加入到混合物中的泡沫量直接控制其密度并因此控制其强度。这归因于增加发泡剂引起的气泡增加了混凝土孔隙率，同时削弱其强度的事实。图1说明了这一事实，其中轻质泡沫混凝土的抗压强度与其密度之间的关系。

另一方面，增加轻质泡沫混凝土的水泥含量能够增强其抗压强度（特别是不包括砂石骨料的泡沫混凝土）。如图2所示。这种趋势的解释是：通过不断的增加水泥，致使与水反应的精细材料增加，导致更多的水合产物与原有的混合物结合，从而增加了强度。此外，事实证明，增加细骨料的粒径会降低轻质泡沫混凝土的硬度。（表1）

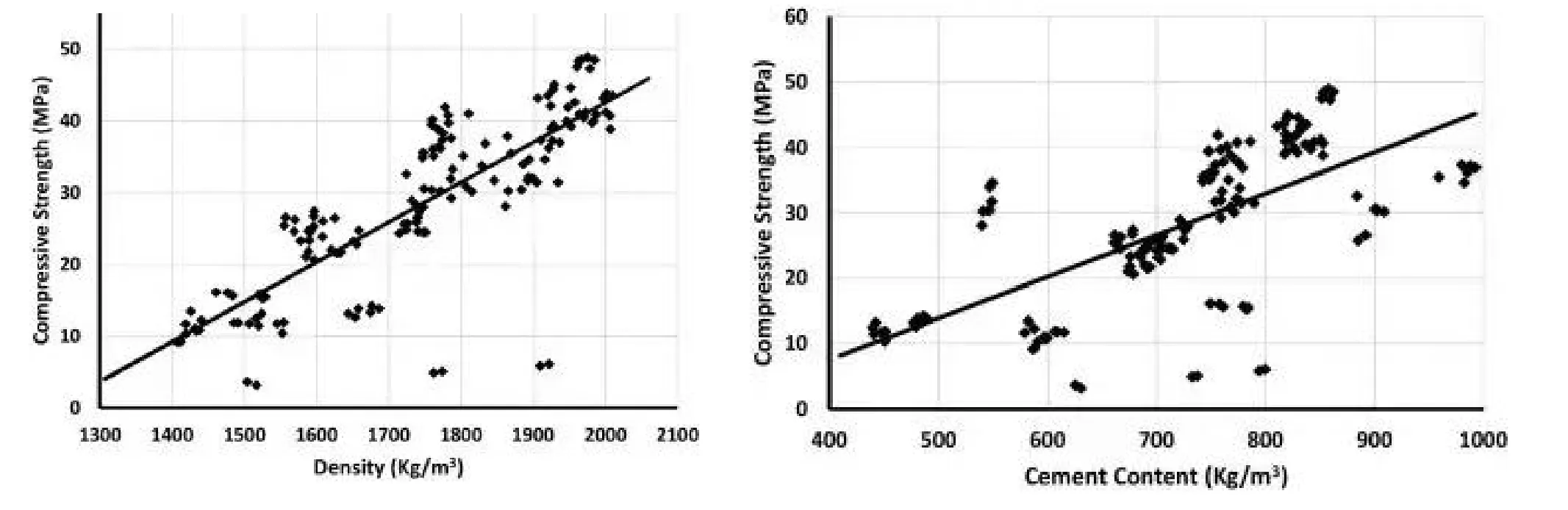
图2：泡沫混凝土的抗压强度与密度的关系

第一，传统多变量非线性回归

为了提前预测泡沫混凝土在第28天的抗压强度，我们使用非线性回归分析了150个样品的数据集。研究的主要变量：密度、水泥含量、砂含量、w / c比、砂粒度、发泡剂、泡沫含量和7天的抗压强度。用于第28天抗压强度的非线性回归的一般模型为：

Var10（相关变量）= 第28天的抗压强度；

V1~V9（独立变量）=输入参数；

分析中使用的损失函数为最小二乘法；

当实际观察与使用开发模型的预测结果相比时，发现相关系数R = 0.97884248，r2 = 0.9581326，置信水平为95%（α= 0.050）。具有标准偏差、t值和p值的模型参数系数（一个）则在表2中列出。

表1：混合比例详细信息

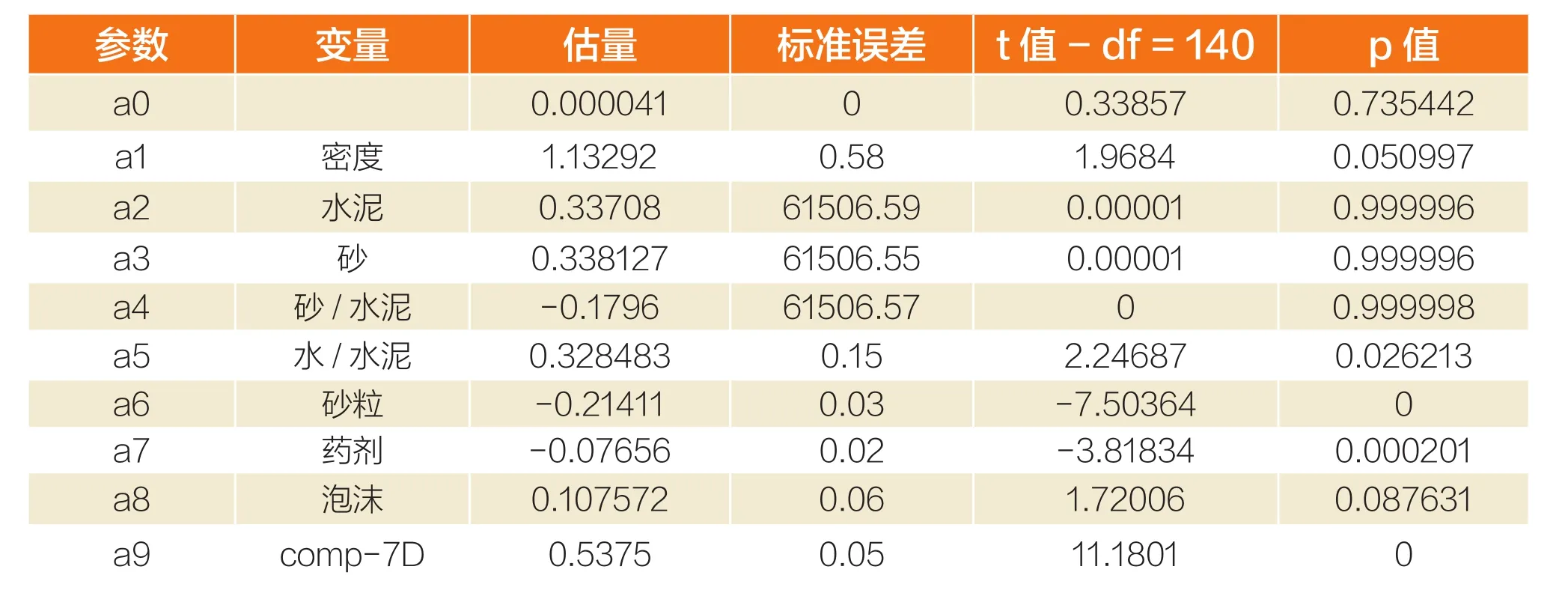
表2：回归模型的系数（参数a）

实际观测结果与回归模型产生的预测结果绘制如图3所示。该图解释了两个数据集之间的高相关性，并反映了所开发的模型的高精度性能。图3（a）中，在围绕30 MPa的抗压强度附近的几个点与实际观测结果略有不同，这可能由于原料的性质（特别是砂的粒度）和所测试样品的具体条件的不同所导致的。

预测结果的差异值反映了开发模型的优良性能。再次，该图展示出了在预测抗压强度方面，每个读数准确的误差量。根据图3（b）可以看出，在30 MPa附近的区间上，模型预测结果与实际观察比较相近，同时，点位分布较多的在（-4和+4）之间的误差范围内。就输入和输出的总相关系数表明，在第28天和第7天，与泡沫混凝土抗压性相关的因素中，密度和水泥含量分别为正方向，w / c比、砂/水泥比和泡沫含量在负方向。

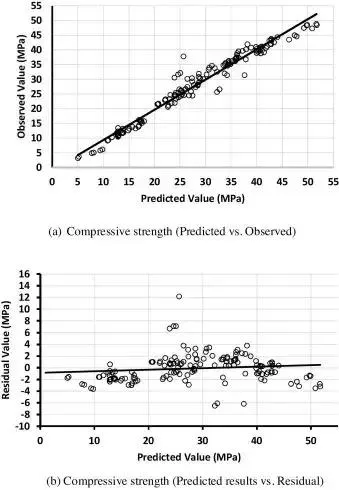
图3：回归模型的性能

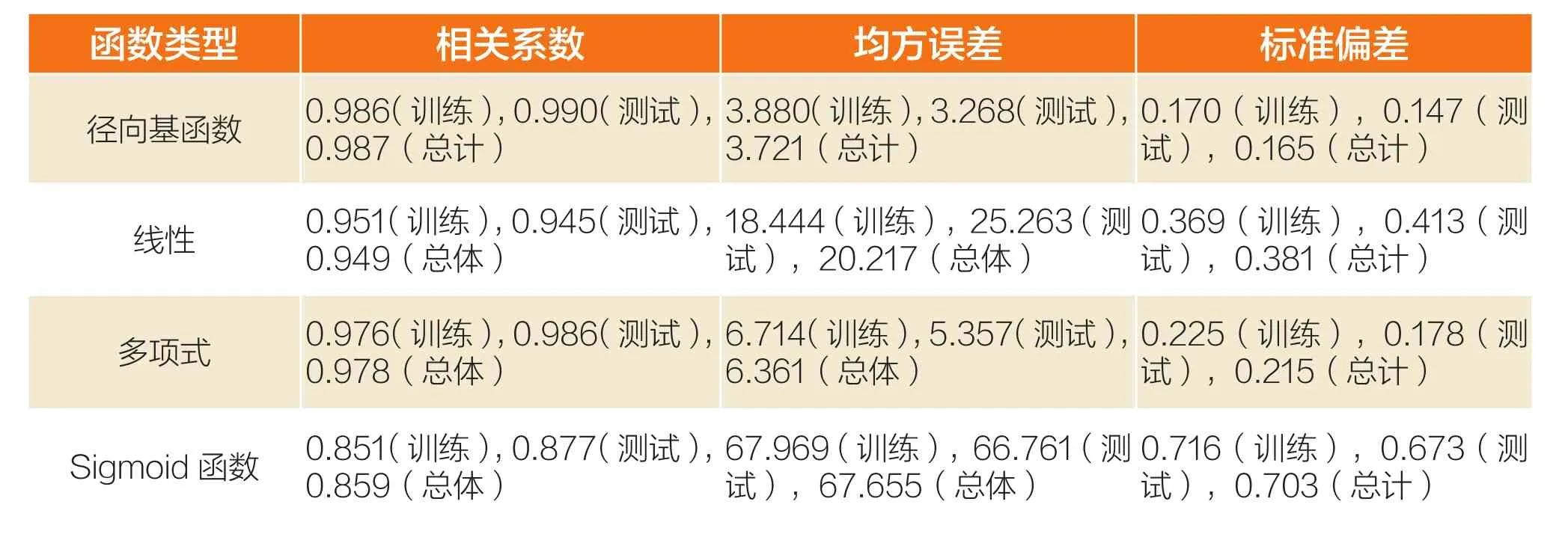
表3：支持向量机的四种类型函数结果

第二，支持向量机

为了实现这种技术，第28天的抗压强度被定义为因变量（Var10），其他输入（V1~V9）作为自变量。将150个整体观察的样本大小随机分为（111个样本）和（39个样本）进行测试，并且采用1型支持向量机进行分析处理。测试了四种核函数类型：径向基函数、线性、多项式和Sigmoid函数。该过程结果列于表3中。

表4：RBF支持向量机模型的主要特点

很明显，在RBF的测试和总体数据集方面，都表现出了最好的高相关性能。它在四个函数中具有最小均方误差，并且具有最小的标准偏差。所以，详细的讨论将集中于RBF来解释这个模型的主要特点。表4中列示出了所有研究的样本，在预测模型中的总误差平均值被发现是（-0.32084），总体相关系数非常显著（约99%），这也反映了开发的模型的高精度。图4则显示了相关数据集（a），测试数据集（b）和总数据集（c）的RBF的预测值作图。可以看出，预测值非常接近图中所有数据集的等式线分布，并且与实际观察到的数据高度相似，这表示所提出的上述模型具有高可靠性。而且，对于每个数据集，我们都为其拟合了最佳的计算公式来绘制分布图。

总结

这项工作主要是对不同混合比例的轻质泡沫混凝土在第28天里抗压强度的变化作了研究。结果显示，密度和水泥含量对混凝土强度产生的影响非常显著，因此，这两个因素对设计泡沫混凝土混合物具有重要的意义。同时，该研究还证明了，随着w / c比、砂/水泥比和泡沫含量的增加，对泡沫混凝土的抗压强度会造成不利的影响。

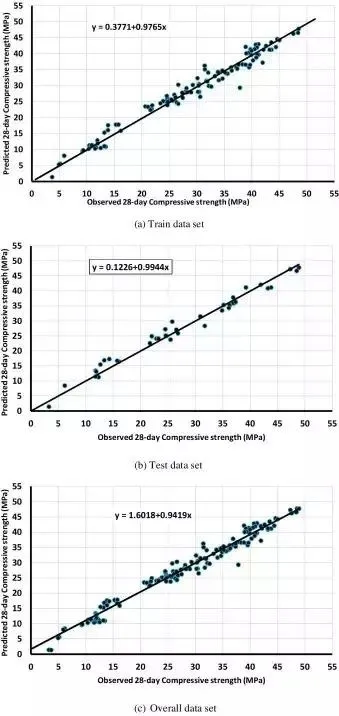
图4：（a）相关数据集（b）测试数据集（c）总数据集

在本研究中，研究者提出了一种用于预测轻质泡沫混凝土抗压强度的数学模型。用于执行所提出的模型的技术包括传统的多变量非线性回归和具有变革性的支持向量机建模。结果显示，本研究中使用的数据集的观察值和预测值之间拥有良好的相关性。所以，这两项技术被称为是最具有吸引力的过程预测工具。事实证明，SVM技术中的径向基函数（RBF）与其他函数和传统回归相比，在预测结果上能够达到最小均方误差和标准偏差。这反映了该种AI相关技术，除了预测整体相关性以外，在预测其它数据集结果方面表现出了非常良好的高精度性。

手机扫码阅读