构筑“题”“图”“型”的共同体
——“里程表问题”的教学研究
2017-06-23四川省成都市高新区锦城小学贾志慧
四川省成都市高新区锦城小学 贾志慧
借助几何直观,可以有效帮助学生提高分析和解决问题的能力。下面结合北师大版三年级上册“里程表问题”内容的系列教学,来谈谈我们的思考。
一、先“图”后文,图生图长
说到几何直观,看图能力的渗透自然是第一步。教学中,教师应有意识地培养学生学会看图,并结合文字进行分析。

图1
如图1,里程表(一)中教材情境既有文字,也有图表。为了培养学生的看图能力,我特意隐去文字(如图2),先直接让学生看图,并交流讨论。
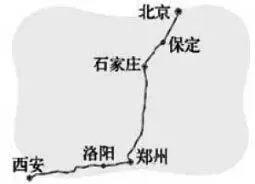
图2
师:通过看图,你们知道了哪些数学信息?
生1:我知道了火车从北京开往西安,途中经过了保定、石家庄、郑州、洛阳这四个站。
师:好的,请大家再看表格(如图3)。你能把这些数据信息标示在图上吗?当然,如果你想用自己喜欢的图式来表达,也可以创作一幅。
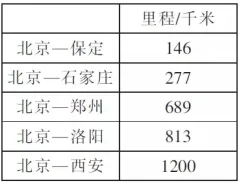
图3
随后,老师根据学生的思考、汇报等,呈现如书本里的象形图、数线图,并交流各种图式之间的异同点,再让学生求解各站点之间的距离。
先图后文或者先文后图,并不是一个简单的先后顺序问题,这里面有教者的设计与思考。在上例中,教师先直接呈现图,并引导学生通过看图、补图、创图等活动,自主探索和发现,思维从具体到抽象,不断延伸。接着,又通过对比,让学生体会到同一问题情境中,“图”的表现形式也是多元化的。这种让“图”生长的过程,其实就是学生把握教量关系、理解题目意义的过程。
二、看题想“图”,借图解题
看图、创图能力的培养固然重要,但能否正确借助图来分析和解决问题,也是学生解题能力形成的标志之一。
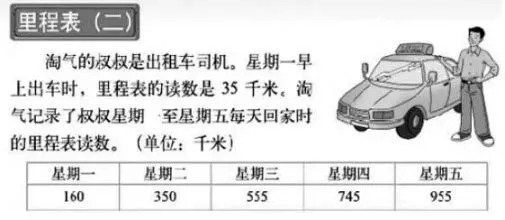
图4
如图4,里程表(二)的教材情境中,要解决的是汽车里程表中的读数问题。由于缺乏类似的生活经验,学生往往难以理解。于是,我做了如下尝试。
老师拿出一本新书,然后开始提问。
师:这是老师新买的一本故事书,还没看呢。要想表示我看的页数,用哪个数比较合适?
生(齐):用0来表示。
师:很好!请用“0”记录下来。我准备周一读到第15页,请接着记录,并想一想我周一读了几页。
教师引导学生用如图5的方式记录下来。
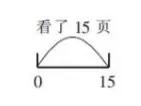
图5
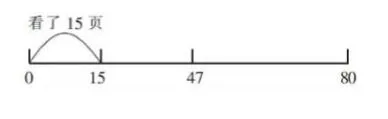
图6
师:我准备周二读到第47页,周三读到第80页。请在原图上继续记录。
教师引导学生记录并完成图6。
师:那么我周二读了几页?周三读了几页? 学生列出算式后,追问算式中每一步计算的道理,顺着学生的说明完善并形成图7。
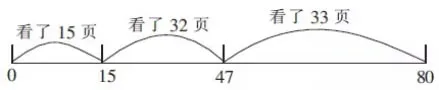
图7
在上面的引导性材料学习完之后,老师呈现图4,放手让学生自主画图表示,然后汇报交流。学生很快便面出了如下的图8:

图8
随后,老师请学生将下面的表格填完整,学生很快便解决了问题。
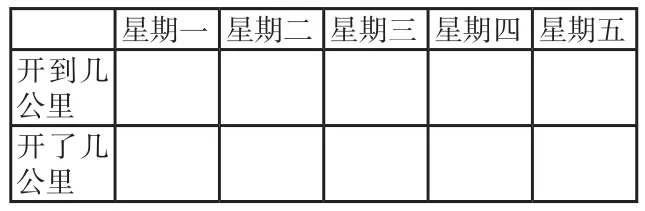
星期一 星期二 星期三 星期四 星期五开到几公里开了几公里
之所以将上述教学做了调整,是因为学生在平时生活中,没有记录汽车里程的经验,不明白“读数”与“里程数”这两个概念的意思。于是,老师举了一个看书的例子,学生对“看了几页”与“看到几页”是有经验的,将这个熟悉的事件用图表达也是轻而易举,再来实现知识迁移就容易多了。在整个学习过程中,老师利用图的直观帮助学生理解数学概念,借图释义,再来解题也就水到渠成了。
三、构“图”得型,图有所成
画图策略的培养,能帮助学生全面建构知识,体会把具体问题抽象为数学模型,从而得出一般的解题方法。当然,画图策略的渗透不应止步于一节课或一种课型。只有让学生多次经历图的产生、形成、发展的过程,有了系统的认识,学生才会把画图策略内化为自己的方法。
在“里程表”知识的复习课上,我是这么做的。
首先,老师在黑板上贴出三条不同颜色的线段(如图9),然后依次捉出如下问题,引导学生层层深入理解分析。
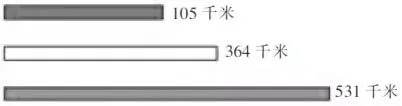
图9
(1)有一列火车是从衢州出发,要经过上饶和南平,再到达龙岩,与其他城市的距离分别是这三条线段的长度。(课件出示图10)

图10
(2)你能把这三条线段合并成一条线路图,让大家一眼就看出火车行走的路线吗?
学生在黑板上展示方法,形成如下的图11。

图11
(3)你能用线段图把它们的关系表达出来,并标上相关信息吗?
学生在作业纸上面一面、标一标,然后展示学生作品。如图12:
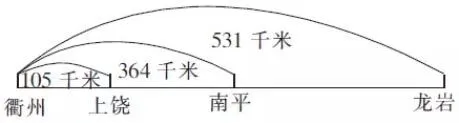
图12
(4)根据这些信息,你能解决什么问题?请列出算式不计算。学生很快呈现如下算式,并解释了每个算式所解决的数学问题。
364-105 531-364 531-305
(5)请你们在图13上标出这几个位置的数据,你会吗?

图13
学生动笔很快有了结果。在反馈时,老师继续提问:刚才的图上,为什么在第一个方框里标的是0?有了前面的层层深入,学生的解释自然合情合理。
在这节复习课中,我有意识地让学生经历“把三条线合成一条线”的过程,沟通了图与图之间的相连、包含等关系,让学生逐步抽象并全面构建出解决“起点为零的里程问题”模型。这样的复习过程,一来厘清了知识的来尤去脉,二来促使学生自我建构以图为媒介的“图型”系统,使得知识的学习更具有迁移的力量。
总而言之,几何直观思想的渗透,需要老师们更多的一些整体设计,站在更高的数学视野上,用更具张力的“图型”来引导单元知识的学习,从而能更好地培养学生灵活解决问题的能力。
