基于忆阻器的PIM结构实现深度卷积神经网络近似计算

李楚曦 樊晓桠,2 赵昌和 张盛兵,2 王党辉,2 安建峰,2 张 萌,2

1(西北工业大学计算机学院 西安 710129)2(嵌入式系统集成教育部工程研究中心(西北工业大学) 西安 710129)

基于忆阻器的PIM结构实现深度卷积神经网络近似计算

李楚曦1樊晓桠1,2赵昌和1张盛兵1,2王党辉1,2安建峰1,2张 萌1,2

1(西北工业大学计算机学院 西安 710129)2(嵌入式系统集成教育部工程研究中心(西北工业大学) 西安 710129)

(lichuxi@mail.nwpu.edu.cn)

忆阻器(memristor)能够将存储和计算的特性融合，可用于构建存储计算一体化的PIM(processing-in-memory)结构.但是，由于计算阵列以及结构映射方法的限制，基于忆阻器阵列的深度神经网络计算需要频繁的AD/DA转换以及大量的中间存储，导致了显著的能量和面积开销.提出了一种新型的基于忆阻器的深度卷积神经网络近似计算PIM结构，利用模拟忆阻器大大增加数据密度，并将卷积过程分解到不同形式的忆阻器阵列中分别计算，增加了数据并行性，减少了数据转换次数并消除了中间存储，从而实现了加速和节能.针对该结构中可能存在的精度损失，给出了相应的优化策略.对不同规模和深度的神经网络计算进行仿真实验评估，结果表明，在相同计算精度下，该结构可以最多降低90%以上的能耗，同时计算性能提升约90%.

忆阻器；PIM；卷积神经网络；近似计算；模拟存储

新型器件忆阻器(memristor)具有能够将计算和存储功能相融合的特殊性质，因此，以忆阻器及其基本单元构造的PIM(processing-in-memory)结构被认为是访存瓶颈的有效解决途径[1].同时，由于欧姆定律和神经网络矩阵乘法运算的高度契合，并且忆阻器的高存储密度也能满足神经网络的巨大数据量，因此基于忆阻器交叉阵列的PIM结构极其适合于实现神经网络近似计算[2].

此前的一些相关研究结果显示，以忆阻器交叉阵列为基础的神经网络计算结构能够有效克服访存瓶颈，并取得良好的加速效果[2-5].然而，数据在交换过程中需要不断经过转换器进行数模/模数转化以及大量的多位中间存储，造成了显著的面积和能量消耗.

因此，本文提出了新型的PIM结构实现基于忆阻器的深度卷积神经网络近似计算，在不降低神经网络计算准确度的前提下，取得了能耗更低、面积更优、执行时间更短的效果.

本文的主要贡献如下:

1) 提出了将卷积过程分解到不同形式的忆阻器阵列中分别计算的计算方案，取得了显著性能提升，最高达到87%；

2) 设计了新型的基于忆阻器的深度卷积神经网络近似计算PIM结构，能够减少数据转换次数，消除中间存储，最高可降低95%的能耗；

3) 针对所提出的结构中可能存在的精度损失，提出了相应的优化策略，提高了系统精度，保证系统精度在95%左右.

1 背 景

1.1 忆阻器阵列的CNN计算特征

卷积神经网络(convolutional neural network, CNN)是神经网络架构中常见的一种，由生物学自然视觉认知机制启发而来.典型的卷积神经网络具有输入层、卷积层、降采样层、全连接层和输出层.一般地，一个卷积层之后配置一个降采样层，2个层构成一组.一个完整的卷积神经网络由一个输出层、多组卷积/降采样层、多个全连接层以及一个输出层按照从输入到输出的顺序构成，如图1所示[6].深度神经网络突出的特征学习能力使其在大数据应用中有突出的表现，特别是语音识别、图像识别等基于分类的识别问题[7].

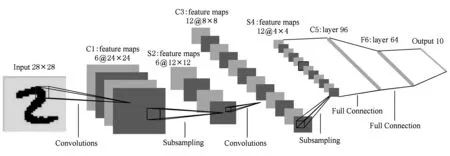
Fig. 1 The structure of LeNet-5 CNN图1 LeNet-5卷积神经网络结构示意图

卷积神经网络的核心是乘累加运算，所有类型的层的算法都可以抽象成乘累加运算.参与乘累加的元素可以分成2类：权值和待处理的信号值.卷积神经网络中所有的运算过程，都可视为权值和待处理的信号值对应相乘之后再累加，其后加上偏置，最后通过激活函数(sigmoid函数)，得到计算结果的过程.即：

(1)

其中,mij为输入，kij为权值，oij为输出.

忆阻器是阻性器件，其电路特性满足阻性器件串并列规则.根据欧姆定律，假设若干忆阻器的一端连接在水平位线WL上，另一端连接在竖直字线BL上，构成忆阻器交叉阵列[8]，第i行第j列忆阻器的阻值为Mij，电导值为gij=1Mij，施加在其WL的电压值为Ui，不考虑外加激励导致的忆阻器阻值变化，则第j条BL的总电流Itotal，j为

(2)

并行地完成多次乘累加运算，如图2所示.所有乘累加有一个元素完全相同，为输入电压Ui；另一个元素不同，为不同列忆阻器的电导值.这与卷积神经网络运算形式的需求一致，如果配置好忆阻器的阻值，将其作为权值，将待处理的信号值编码成输入电压，就可以完成权值和待处理信号值的乘累加[9].

Fig. 2 Circuit structure of the memristor array图2 忆阻器阵列的电路结构

乘累加的计算结果形式为电流值，需要经BL输出到外部，以稳定的形式存放在存储单元中.如果神经网络的规模或深度超过单个忆阻器阵列的计算能力，则可分离出一部分忆阻器阵列作为缓存，用于存储中间结果，减少与外部的数据交换.

1.2 相关工作分析

文献[10-12]研究了基于非易失性存储器的PIM结构，证明了该结构在加速和降低能耗2方面都有显著优势.文献[3]提出了一种新型的PIM结构，利用忆阻器交叉阵列和CMOS辅助电路实现了CNN，并将忆阻器交叉阵列划分为2种不同功能的模块:1)只用于存储;2)兼用于存储和计算.该电路结构取得了明显的加速效果，计算精度也较高.然而，其计算过程中产生的中间结果近似于模拟值，而忆阻器单元使用的是数字忆阻器，数据无法缓存，需要不断地进行数模/模数转化以及大量多位的中间存储，造成了额外的面积开销和能量消耗.

如果使用模拟忆阻器，即阻值连续可变的忆阻器，则可以保证中间结果能够缓存在忆阻器阵列中，消除数据转换带来的额外消耗.并且将读写次数由多位读写压缩至一次读写，大大提高数据密度，降低读写消耗.虽然理论上模拟忆阻器存储时拥有无穷高的精度，但是在实际应用中，由于相邻存储单元之间的漏流干扰和读写误差等原因，模拟忆阻器的精度会受到影响.同时，数字忆阻器存储多位数据时也存在截断误差，因此不能简单地判定二者的精度大小.如果能够通过合理的措施保证模拟忆阻器的精度，就能够利用其显著提高数据密度，大大降低计算电路的复杂性.

文献[8]提出了一种基于模拟忆阻器的非线性神经网络计算方案并验证了其可靠性，结果表明其平均误差在5%左右.

基于以上分析，本文采用模拟忆阻器构建深度CNN近似计算结构，通过分析卷积神经网络的计算特征，将计算过程分解成利于并行的2部分，将中间结果缓存在部分忆阻器阵列中，消除数据转换.同时，给出提高精度的措施保证系统的可靠性.

2 基于CNN计算分解的忆阻器阵列结构

2.1 面向高效并行的计算方案

考虑到卷积层是卷积神经网络中复杂度最高、最具有普遍意义的类型，降采样层和全连接层都可以看作是卷积的特殊形式，只要能够实现卷积层，采用类似的方法也能实现降采样层和全连接层.因此以下重点讨论卷积层的实现方法.

假设卷积层的输入图尺寸是n×n，卷积核尺寸是k×k，滑步长度是l，则该层的输出特征图尺寸为(n-k+l)l×(n-k+l)l.以MNIST手写体识别[13]的第1层卷积层计算为例，输入图大小是28×28，卷积核的大小是5×5，滑步是1，得到的特征图大小是24×24.

单次卷积运算由一个k×k的卷积核和一个k×k的卷积计算窗口参与.具体到MNIST手写体识别的第1层卷积层中，单次卷积运算是5×5的卷积核和5×5的卷积计算窗口.把计算过程进行分解，可视为6次乘累加运算.其中前5次是并列的，每次由卷积核中的一行和卷积窗口中的一行进行乘累加；最后一次是在前5次计算的中间结果得出后，将5个中间结果全部累加.这样拆解的原因是：在忆阻器阵列电路中，批量读取数据往往是以行为单位，在同一行的数据可以在一个周期内同时读出，同时参与运算；而不在同一行的数据，需要在另外一个周期才能被读出.通过此拆解方法，将单次卷积运算分成了二维方向的2种类型运算：1)横向k次乘累加;2)纵向1次累加.

图3给出了一个卷积运算拆解的例子，原本的四次乘法、一次加法被拆分成了2组三次乘累加.

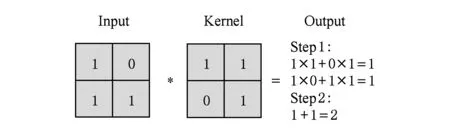
Fig. 3 An assembly example of 2×2 convolutional computation图3 一个2×2卷积运算的拆解示例

本文将拆解后的2种运算分到2个忆阻器阵列子电路模块中分别计算，能够减少读取次数、提高效率并保证数据大规模并行.用于计算横向乘累加的模块命名为权重子阵列(weight sub-array, WSA)，因为权重的存储和参与运算都在这部分中；用于计算纵向累加的模块命名为累加子阵列(accumulate sub-array, ASA)，因为它一方面起到缓存卷积中间结果的作用，一方面将这些中间结果进行累加得到卷积值.

2.2 WSA模块

WSA模块的作用是完成横向乘累加，即卷积核中的每一行与卷积窗口中的每一行的乘累加运算.为了消除潜通路径(sneak path)的影响，其结构是1S1R的忆阻器单元构成的阵列[14](为简化电路结构图，便于阅读，以下模块结构图中省略了与忆阻器串联的选择管).

传统的策略是将卷积核(即权值)数据和卷积窗口数据编码为忆阻值，以矩阵排列方式分别存储在2个阵列中.计算时将卷积窗口数据读出，转换为电压形式，再作为输入传递给权值数据所在的阵列，最后在这其中将二者相乘并叠加.每采集一次卷积窗口数据需要进行一次读操作读取一行，进行一次k×k大小的卷积需要进行k次读操作才能采集完全部输入数据.进行完本次乘累加运算后，则滑步一次进行下一次卷积运算.由于前一次的读取结果不能以电压形式被缓存，此时需要再次读取同样的k行.当滑步进行到一行的末尾，则回到起始位置并向下滑步一次进行下一次卷积运算.此时需要读取的数据中只有一行不重复，其他k-1行都与前一次卷积读取的行相同.

由于卷积层算法中每个卷积窗口都存在重叠，以及阵列按行读取数据的特点，大量的时间和能耗消耗在了对重复数据的多次读取上.要避免重复读取，首先要观测每次读取的数据参与的运算次数.下文继续以MNIST手写体识别的第1层卷积层计算为例，输入图大小是28×28、卷积核的大小是5×5，滑步是1，得到的特征图大小是24×24.将输入图的第i行命名为Li，将卷积核按照从左到右、从上到下的顺序命名为w1～w25.

以输入图为观测对象，逐行考查：

对第1行L1，只有卷积核覆盖在L1～L5上做卷积时参与运算，所涉及到的运算为24次乘累加.从L1最左边开始，每次取5个连续数与w1～w5分别相乘并累加，然后右移一个单位继续取数，直到取到最右边的5个数，共24次乘累加.

对第2行L2，卷积核覆盖在L1～L5或者L2～L5上做卷积时都要参与运算，所涉及到的运算为24×2次乘累加.从L2最左边开始，每次取5个连续数，不仅要与w1～w5相乘并累加，还要与w6～w10进行相同的操作.

对第3行L3，卷积核覆盖在L1～L5，L2～L5或者L3～L4上做卷积时都要参与运算，所涉及到的运算为24×3次乘累加.从L2最左边开始，每次取5个连续数，不仅要与w1～w5相乘并累加，还要与w6～w10，w11～w16进行相同的操作.

以此类推，L4要与w1～w5，w6～w10，w11～w15，w16～w20进行24×4次乘累加，而L5～L24要与w1～w5，w6～w10，w11～w15，w16～w20，w21～w25这5组数进行24×5次乘累加.

最后5行的规律与前5行对称，L25与w6～w10，w11～w15，w16～w20和w21～w25进行24×4次乘累加，L26与w11～w15，w16～w20和w21～w25进行24×3次乘累加，L27与w16～w20和w21～w25进行24×2次乘累加，L28与w21～w25进行24次乘累加.

至此，输入图每一行参与运算的情况分析完毕，其对称性和规律性有利于在电路中进行优化.由于计算的总次数是固定的，或者扩大阵列面积，在一个时间周期内并行地进行多次计算；或者复用阵列，在每个时间周期进行一次计算，因此计算时间和面积相互制约.由于忆阻器的纳米级尺寸和高密度集成，其面积明显小于CMOS电路，阵列面积的增加并不是电路的主要制约因素，因此将时间作为主要优化参数.WSA的设计目标是：增加并行性，在每次读操作之后，将读出的一行所涉及到的所有乘累加运算在一个周期内全部完成.

根据以上分析，将权重分为w1～w5，w6～w10，w11～w15，w16～w20，w21～w25五组，构建5个阵列分别存放.在每个阵列内，不再按照传统的数据存放方式，而是将5个数据扩展成一个28×24的阵列，每一列由前一列的数据向下移位一次构成.以w1～w5所在的阵列为例，排列方式如图4所示，第1列为w1～w5从上到下排列，第2列为第1列向下移位一个单位，以此类推，直到填满第24列.

Fig. 4 Structure of the first array of 28×24 WSA图4 28输入24输出的WSA中第1个阵列的结构图

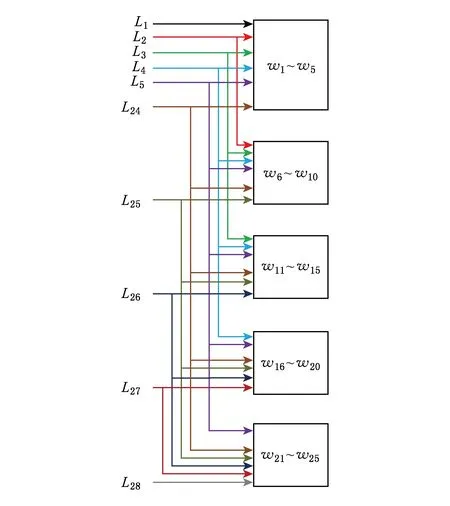
Fig. 5 The data transmission relationship between the rows of input map and the WSA图5 输入图的行数与WSA阵列的数据传输关系

每个周期内读出一行输入图的值，按照图5所示传递给与之相关的阵列.对于每一个阵列，输入为一行的28个数据，以电压形式从28条WL同时并行输入.输出为24个乘累加的计算结果，以电流形式从24条BL同时输出.

假设一个周期内5个阵列的输入为ai,j，输出分别为bi,n，ci,n，di,n，ei,n，fi,n，其中ai,j表示第i行第j列的输入数据，每个周期输入一行，在此周期内i不变，j从0到最大值遍历一次.bi,n～fi,n分别表示5个阵列中当输入数据为第i行时的第n条BL上的输出数据(1≤i，j≤28，1≤n≤24).

以w1～w5所在的第1个阵列为例，BL1从上到下存放w1～w5，则BL1的输出为ai,1～ai,5与w1～w5的按序乘累加.BL2是BL1的数据下移一位，则BL1的输出为ai,2～ai,6与w1～w5的按序乘累加.可以得到：

bi,n=ai,n×w1+ai,n+1×w2+ai,n+2×w3+
ai,n+3×w4+ai,n+4×w5.

(3)

其他4个WSA阵列以相同的形式分别将w6～w10，w11～w15，w16～w20，w21～w25错位展开存放.同理可得：

ci,n=ai,n×w6+ai,n+1×w7+ai,n+2×w8+
ai,n+3×w9+ai,n+4×w10,

(4)

di,n=ai,n×w11+ai,n+1×w12+ai,n+2×
w13+ai,n+3×w14+ai,n+4×w15,

(5)

ei,n=ai,n×w16+ai,n+1×w17+ai,n+2×
w18+ai,n+3×w19+ai,n+4×w20,

(6)

fi,n=ai,n×w21+ai,n+1×w22+ai,n+2×
w23+ai,n+3×w24+ai,n+4×w25,

(7)

对一幅输入图，28行被分成28个周期按序输入，在第k个周期可以得到bk,n，ck,n，dk,n，ek,n，fk,n.每一个卷积运算分成的5次乘累加在5个周期内完成，例如输出图的第一个卷积结果k1,1：

(8)

即

k1,1=b1,1+c2,1+d3,1+e4,1+f5,1.

(9)

5次乘累加被分在第1个到第5个周期完成.同时，与k1,1同在一行的第1行24个数据都是在第5个周期将5次乘累加全部计算完.而第2行的24个数据在第6个周期能将5次乘累加全部计算完.第28个周期结束后，全部输出数据都被计算完毕，共24×24×5个.每个周期结束后，这些中间结果值需要被缓存进行下一步累加，这部分工作传递给ASA，由ASA完成.将WSA中完成横向乘累加输出的中间结果命名为部分和.

在以上示例中，整个WSA需要28×24×5个忆阻器单元.更一般地，若输入图大小是n×n、卷积核的大小是k×k，滑步是l，则需要n×(n-k+l)×k个忆阻器单元.

对于降采样层，可将其视为特殊的卷积层，其特殊之处在于：1)卷积窗口没有重叠；2)所有权值都是相同的(取均值算法).除此之外，乘累加的顺序和方法均无改变.在降采样层的计算初始时，将滑步设置为与卷积核宽度同样的大小k，将权值设置为同一个固定的数，则采用的计算电路和卷积层可统一成同种形式.对于全连接层，与前2种层不同，只有1次乘累加过程，而没有部分和.这是由于全连接层的输入数据只有1行，不需要进行纵向叠加.因此，全连接层可以直接映射到WSA，在1个周期内计算完成，而不需要传输给ASA再做叠加.

该设计可以避免电路的特殊化，同样的硬件电路通过配置可以任意改变为卷积层、降采样层或全连接层，保证了电路的可配置性.

2.3 ASA模块

ASA模块的作用是完成纵向乘累加，即接收由WSA计算得出的部分和，完成进一步叠加，从而完成卷积运算.叠加过程没有加权，直接将所有值相加.其结构是若干模拟忆阻器缓存单元构成的阵列，每个缓存单元由1个忆阻器和1个双向选择管构成，如图6所示，圆形虚线框内为1个单元.

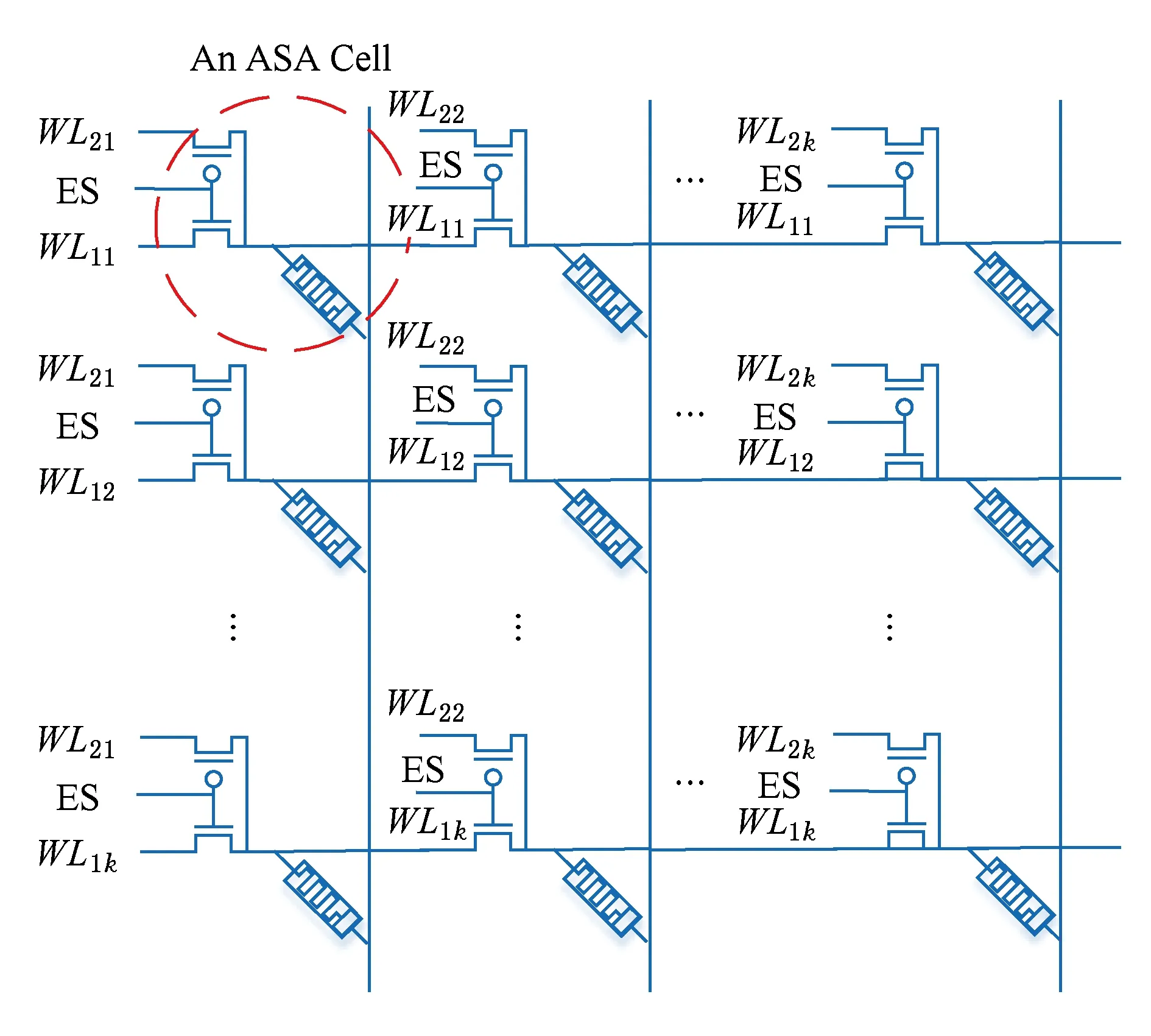
Fig. 6 The structure of ASA图6 ASA的结构

ASA的输入信号分为2部分：1)控制器以高/低电平形式输入到双向选择管的控制信号ES(extra selector)；2)从WL以电压形式输入的部分和数据.

双向选择管有2个作用：1)充当忆阻单元选择管，消除Sneak Path；2)将WL扩展成2个不同的输入端WL1和WL2，在不同情况下为其对应的忆阻器选择合适的输入信号.当ES信号为高电平1时，忆阻器缓存单元中的NMOS晶体管导通，PMOS晶体管关断，信号从WL1输入；当ES信号为低电平0时，PMOS晶体管导通，NMOS晶体管关断，信号从另外一条扩展字线WL2输入.

根据WSA模块的设计，需要在同一个ASA中叠加的k个部分和数据，即一个卷积运算的所有部分和数据将会在连续的k个周期内产生，以模拟电压信号的方式输出.部分和电压信号输入给ASA，由电压的幅值大小决定对ASA中的忆阻器的写入值.写电路驱动电压的幅值与写入的电阻值一一对应，理想条件下，二者呈线性关系.ASA中所有忆阻器的阻值在初始化过程中都被写入为最小阻值，可以视为0.随着WSA不断输出部分和，ASA也不断地被连续写入阻值，在每个单元内积累写入值，从而完成对部分和的累加，1个计算周期结束后忆阻器的阻值对应着卷积结果.

继续以MNIST手写体识别的第1层卷积层计算为例，输入图大小是28×28、卷积核的大小是5×5.在每个周期内，WSA电路的5个阵列各输出24个部分和.从第1个运算周期开始，每5个周期视为一个循环，同一周期内输出的所有部分和不存在需要叠加的关系，需要叠加的是第i个周期WSA的第i个阵列内同一编号的BL上输出的结果(1≤i≤5).每一个卷积运算的最终结果都是由5个部分和叠加而来的，以下集中讨论输入图前5行与卷积核进行卷积的计算结果，将这一部分输入图的第j行与卷积核的第j行乘累加产生的部分和称为部分和j(partial sumj).

卷积运算开始的第1个周期，WSA的第1个阵列输出的是输入图第1行的每5个元素与w1～w5分组相乘累加的24个结果，即部分和1，其他4个阵列没有输出结果.将这24个结果通过WL1k同时传输到ASA的第1列上，以阻值形式缓存.

第2个周期，WSA的第1个阵列输出的是输入图第2行的每5个元素与w1～w5分组相乘累加的24个结果，第2个阵列输出的是输入图第2行的每5个元素与w6～w10分组相乘累加的24个结果，即部分和2，其他3个阵列没有输出结果.根据卷积神经网络的算法，部分和1应该与部分和2相叠加.那么，将第1个阵列输出的结果通过WL1k传输到ASA的第2列上缓存，而将部分和2通过WL21再次传输给ASA的第1列，给忆阻器写入叠加值，叠加在部分和1上.

同样地，在第3和第4个周期，每个周期利用WL1k缓存一列数据，利用WL2k叠加一次部分和.

第5个周期结束时，ASA的前5列中存有缓存数据，第1列上已经完成了5个部分和的累加，即卷积结果图中第1行的24个数据.为了节省面积开销，计算完毕的数据可以马上输出到外部或者下一个层，将第1行的忆阻器单元回复初始状态，即最小阻值状态，可以在下个周期缓存新的数据.

需要注意的是，此时ASA的第2列上已经完成了卷积窗口下移一个单位时，即输入图的第2行到第6行与卷积核做运算的前4个部分和的叠加，只要第6个周期结束，这部分卷积运算，即卷积结果图中第2行的24个数据就计算完成，也可立即输出到外部，重置第2列的忆阻器单元.

通过这样流水的方式，完成全部卷积运算的周期数被大大缩减，只需28个读周期结束，WSA计算出所有部分和后，ASA就能立即输出所有的卷积结果.整个计算过程中每个周期的输出如表1所示，表1中的LINEi表示输入图中的第i行，Ok，n表示输出卷积结果的第k行中所有元素.

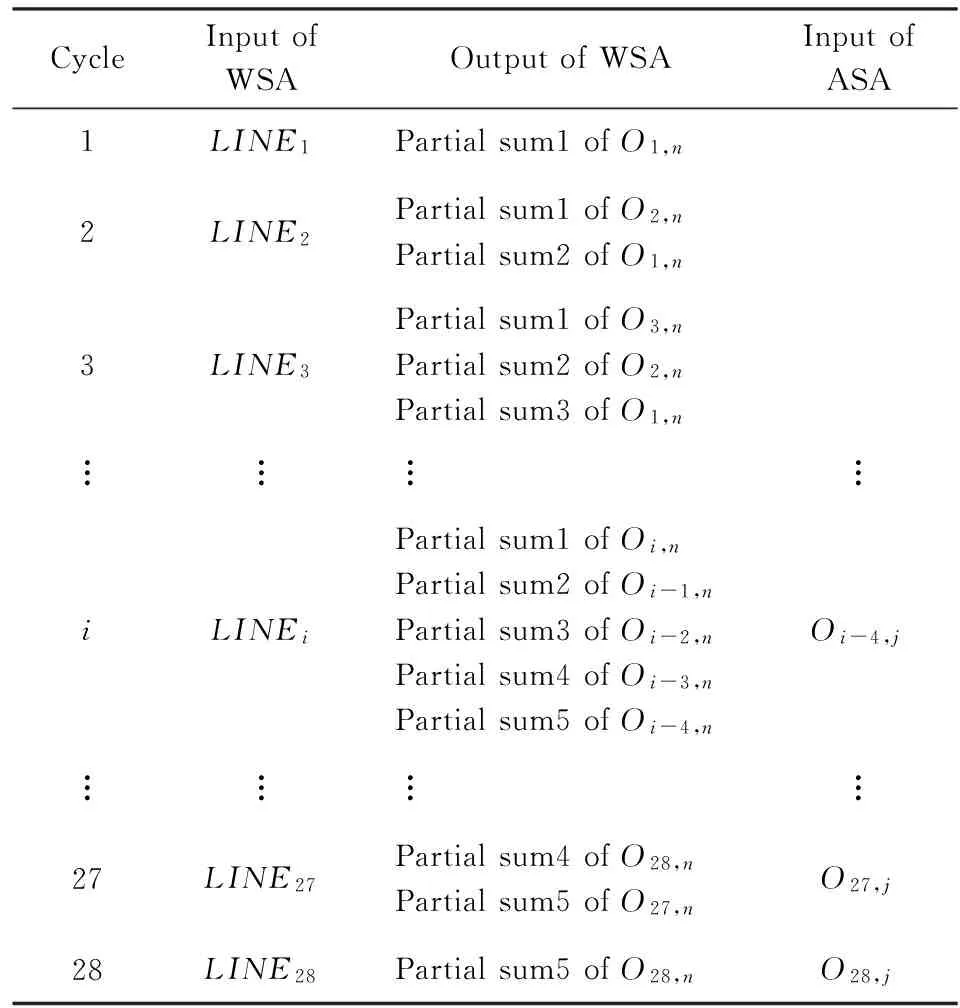
Table 1 The Input and Output of WSA and ASA in Each Cycle

此外，由于WSA中忆阻器的乘累加计算依赖于欧姆定律，当电压激励给出后，电流响应的延迟时间极短；ASA中的叠加依赖于忆阻器的连续写入，由于忆阻器的读写速度快，ASA延迟时间也极小.因此整个计算结构无论在周期数还是电路延迟时间上都体现出显著的速度优势，对加速卷积神经网络有着极大提升.

整个ASA需要28×24×5个忆阻器单元，包含1个忆阻器和2个互补MOS晶体管.更一般地，若输入图大小是n×n,卷积核的大小是k×k，滑步是l，则需要n×(n-k+l)×k个忆阻器单元.

3 面向CNN近似计算的PIM结构

3.1 PIM系统结构

本文设计了一种基于忆阻器阵列的可配置CNN近似计算PIM结构(如图7所示).系统包括16个分块(bank)，被划分为7种模块，分别为：全局控制器(global controller, GC)、数模(模数)转换器(DAC/ADC)、三输入多路选择器(multiplexer, MUX)、读写模块(write and read, WR)及其寻址模块(addressing, AD)、开关模块(switch, SW)、WSA和ASA.

1) 全局控制器.①在系统开始工作之前，根据不同深度和规模的卷积神经网络应用，从bank和bank内的模块2个层面来进行配置和调度.在bank层面，当所需求的CNN应用的深度和规模超过一个bank的运算范围时，全局控制器将配置多个bank协同运算，把需要运算的数据分解到各个bank中并行计算，每个bank运算后的数据会按照层的顺序输出给下一个bank作为输入.在阵列层面，全局控制器将根据所需规模调用适合大小的阵列进行计算，剩余不被调用的部分不参与计算，保持在存储模式.②在系统工作过程中，通过控制信号控制整个系统的工作流程.全局控制器中配有计数器和时钟产生模块，在每个周期给WR，WSA，ASA等模块发送控制信号，使其正常工作.

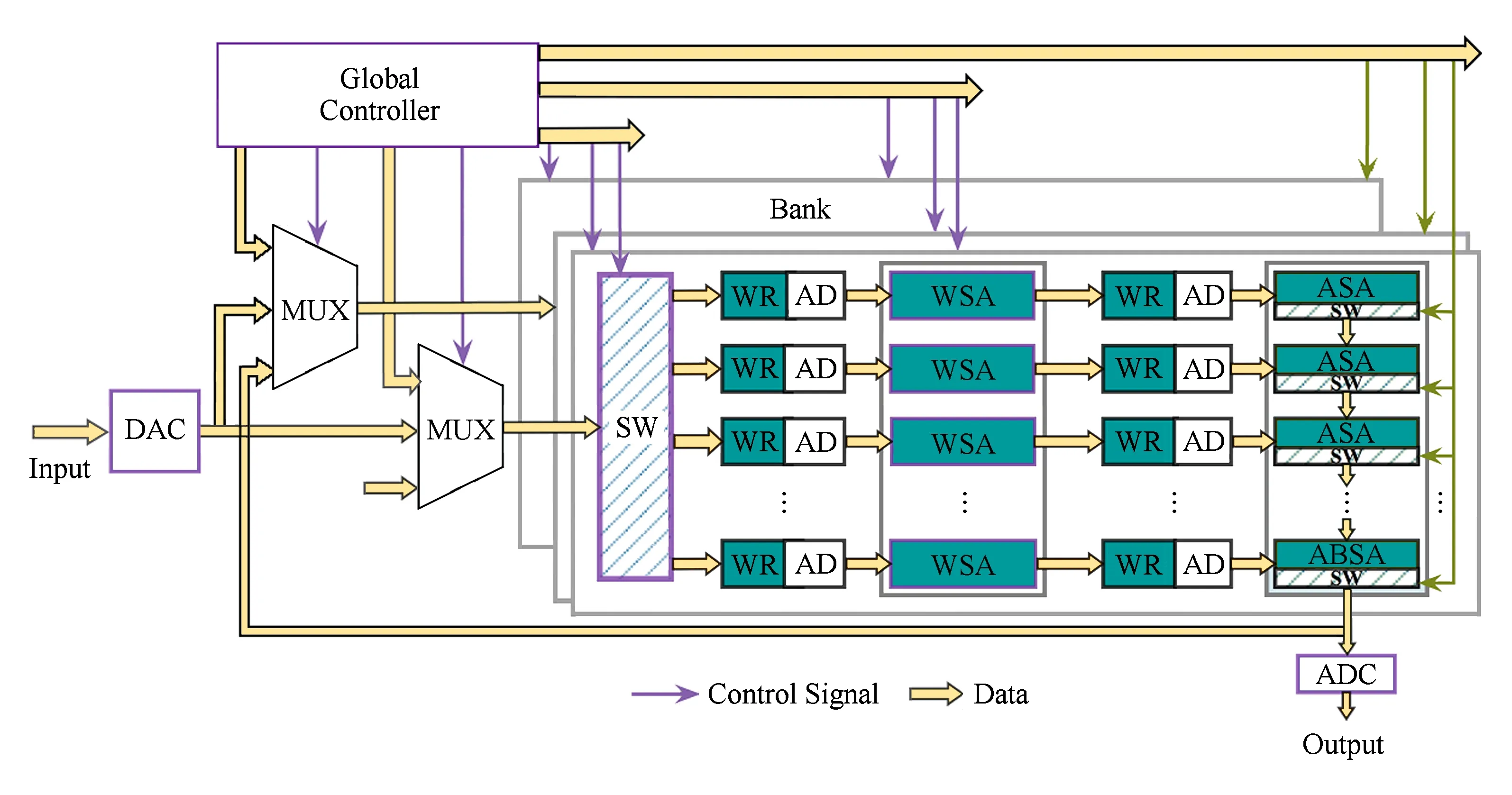
Fig. 7 Configurable PIM structure for CNN approximate computation图7 可配置卷积神经网络近似计算PIM结构图

2) 数模(模数)转换器.将外部输入的数字信号转换为模拟电压信号，作为bank的输入信号参与CNN运算.运算完成后，再将输出到外部的模拟信号转换为数字信号.为了降低功耗和面积开销，一组数模(模数)转换器可以由多个bank共享，分时使用.本设计中采用4个bank共享一组数模(模数)转换器的方案，即一个系统中含有4组数模(模数)转换器.

3) 三输入多路选择器.在不同阶段为bank选择合适的输入信号.输入信号来自于不同来源：①初始化过程中来自全局控制器的配置信号；②外部输入信号经过数模转换后产生的模拟信号；③前一层的输出信号.

4) 读写模块.为阵列中的忆阻器写入值，写入包括2个过程：①初始化阶段.根据线下训练的结果为WSA写入权重矩阵对应的阻值，为ASA写入最小阻值RON.②计算阶段.根据WSA输出的驱动电压为ASA实时地连续写入阻值.每个读写模块附带一组寻址模块(AD).

5) 开关模块.为WSA选择输出计算结果到外部或继续缓存数据.开关模块的开断情况收到全局控制器的控制.

3.2 PIM系统控制流程

WSA可以被配置计算或存储2种模式，而ASA只能在计算模式工作.在没有计算请求时，WSA全部保持存储模式(memory mode).当一个CNN应用的计算请求命令到来，系统将进入计算模式(computing mode)，整个过程分为初始化(initial phase)、计算求值(valuing phase)2个阶段：

1) 初始化阶段

① 输入神经网络配置参数并进行配置

分析应用需求，给全局控制器输入神经网络的参数，包括：网络的层数、各个层的种类、每层的输入和输出数量等.根据参数对阵列进行配置，分配好参与计算的bank，划分出bank中参与计算的单元，按照顺序配置成不同的层.对于卷积层或降采样层，配置一个WSA和一个ASA结合；对于全连接层，只配置一个WSA，没有ASA.设置好数据接口，令不参与计算的单元保持在存储模式.

② 初始化所有阵列的忆阻值

对于卷积层和全连接层的WSA，通过MUX的选择，从外部经过数模转换输入线下训练的权值给读写模块，然后按照错位展开的方式排列，通过WR将阻值写入到对应WSA的各个单元中.

对于降采样层的WSA，写入值为固定的某常数，这里设定为忆阻值最大值和最小值的中位数，即(RON+ROFF)/2.对于卷积层和降采样层的ASA，写入值为忆阻值的最小值，即RON.

2) 计算求值阶段

① 从外部输入计算数据，经过DAC转换成模拟值，再通过MUX的选择输入给第1层对应的WSA.根据神经网络应用的不同，第1层有可能是卷积层，也有可能是降采样层.在第1层的WSA中计算出所有部分和，实时地通过BL输出给第1层的ASA的写电路，写电路对ASA进行改写，完成部分和的叠加.最后将计算结果通过ASA的BL输出.

② 第1层计算完毕之后，将输出数据通过MUX传输给下一层，进行下一步计算.自此计算流程与第1步相同，直到所有卷积层和降采样层计算完成.在计算电路中流动的数据全部为模拟电流或电压值，不需要经过数模/模数转换.

③ 所有卷积层和降采样层计算完成之后，数据传输给全连接层.全连接层没有ASA，在WSA中进行乘累加即可得出计算结果.将计算结果经过ADC传输到外部，标志着整个计算过程完成.

④ 计算完成之后，全局控制器将WSA恢复为存储模式，将ASA中缓存的所有值释放.

4 精度提高的优化策略

模拟忆阻器的噪声敏感度远远高于数字忆阻器，噪声干扰会影响系统的准确性和灵敏性.经过分析，本系统噪声来自于若干并列的噪声来源，可以表示为由这4个主要元素构成的表达式，如式(10)所示：

Noise=E{θl,θm,θw,θo},

(10)

其中θl表示来自于漏电流(leakage)的噪声，包括Sneak Path和MOS器件漏电等;θm表示来自于从权值到非线性忆阻值(memristance)的映射误差;θw表示来自于写入过程(writing)的误差;θo代表其他来源(other)的噪声，包括但不限于器件噪声和过程噪声等.

θl和θw可以在电路设计过程中采取措施来消除对电路的干扰影响.对于θl，本文中使用给忆阻器串联选择管构成忆阻单元的方法加以消除，对于θm,θw和θo，分别采用权值映射的修正函数、读写模块的精度提升和噪声感知的训练方法来消除.

4.1 权值映射的修正函数

θm来自于从权值到非线性忆阻值的映射误差.在神经网络计算的初始化阶段，要完成从训练好的权值到WSA中忆阻值的一一映射，并将其写入相应的忆阻器中.一般采用的映射函数是线性函数，也就是说，2个权值w1,w2的差值和与之对应的2个忆阻值M1,M2成正比关系，即ΔMΔw是恒定常数.然而，忆阻器物理器件是一个非线性器件，忆阻值M和流经的电荷量Q呈非线性关系，2个忆阻值M1,M2的差值和与之对应的2个电荷量Q1,Q2不成正比关系，即ΔMΔw不是恒定常数.也就是说，在不同的初始条件下流过相同的电荷量时，忆阻值的变化量不恒定.本文所用的忆阻器模型仿真曲线如图8所示，其中图8(a)是I-V曲线;图8(b)是M-Q曲线，即忆阻器阻值和电荷量的关系曲线.

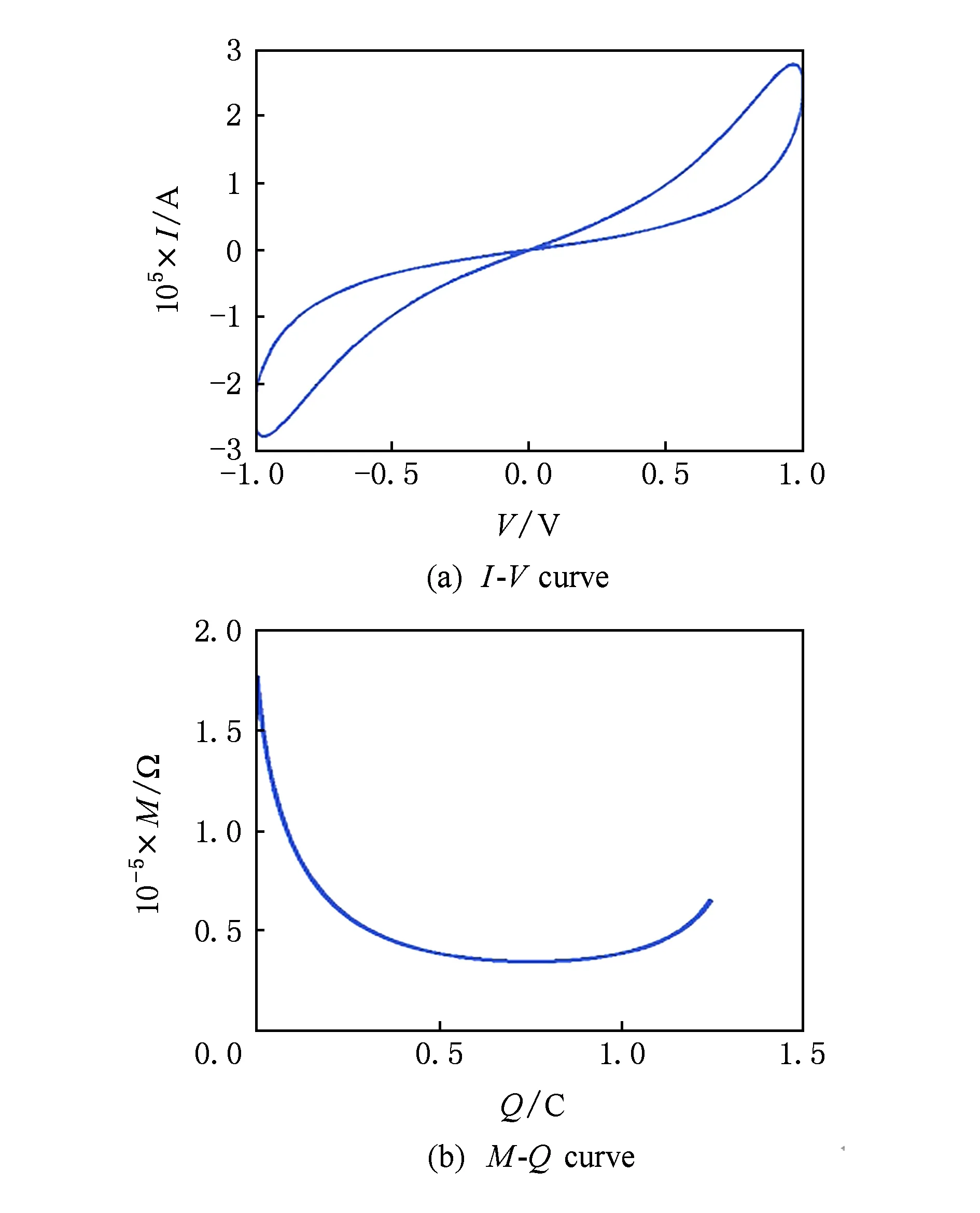
Fig. 8 The memristor model simulation curve图8 忆阻器模型仿真曲线

如果采用传统的线性映射方法，忆阻器器件的非线性成分就会导致在计算值累积的过程中产生误差.实验表明，在一层输入为28×28、卷积核大小为5×5、滑步为1的卷积层计算情况下，线性映射方法会造成的输出值相对误差大约为10%.在多层卷积神经网络中，这个误差将会进一步累积，如果不采取优化措施，有可能会直接导致计算结果错误.

为了解决这一问题，本文提出了一种新的修正映射方法.假设训练好的权值位于[Bl，Bh]之间，其中Bl表示权值的下边界，是所有权值中的最小值；而Bh表示权值的上边界，是所有权值中的最大值.确定好范围之后，将其与位于[RON，ROFF]之间的忆阻值通过修正的映射函数进行映射.

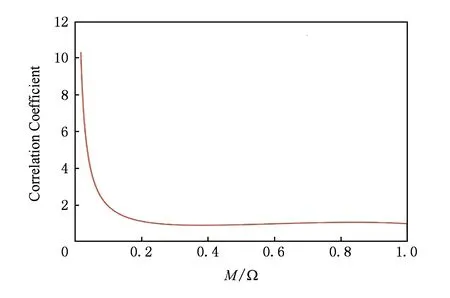
Fig. 9 Mapping function correction curve图9 修正映射函数曲线

修正映射函数是通过将原本的线性映射函数和非线性的M-Q曲线相除，再利用Matlab进行多项式拟合得到.经过试验，当多项式的次数为9时，能够在[RON,ROFF]取值范围内对本文所使用的忆阻器模型取得较贴近的拟合效果.该修正映射函数为

(11)

其中,M为自变量，代表忆阻值；f(M)为因变量，代表修正映射函数；p0～p9为10个常数，是通过Matlab拟合得到的系数.修正映射函数的曲线图如图9所示:

采用这个修正拟合函数，可以消除非线性因素带来的误差，将识别准确度提高7%左右.

4.2 读写模块的精度提升

在忆阻器阵列中，大量的导线WL/BL平行放置，会造成寄生电容的引入.寄生电容在忆阻器的写入过程中会被写驱动充电，发生电荷共享，消耗一部分写驱动电荷，造成写干扰.由于大规模阵列中的连接线长度大、数量多，寄生电容的值较大，造成的干扰也更加严重.根据文献[15]中的分析，写干扰的程度与位线寄生电容CBL成正比，与写电流ISET成反比，如式(12)所示.也就是说，阵列尺寸的增大或者写电流的减小都会增大写干扰，这与高密度、低功耗的目标相悖.

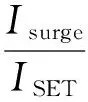
(12)

本文通过对寄生电容进行预充电的策略消除寄生电容的影响.带预充电电路的写电路如图10所示，在文献[16]的写电路基础上增加了预充电单元.图10中Spre是预充电控制开关，Ipre是预充电电流源.在写操作前添加预充电阶段，将开关Spre接Port1，给寄生电容施加一个短时间的预充电电流.预充电电流的持续时间和幅值选择基于阵列的大小和写入电压的值.预充电完成后，将开关Spre接Port2进行忆阻器的脉冲写操作.

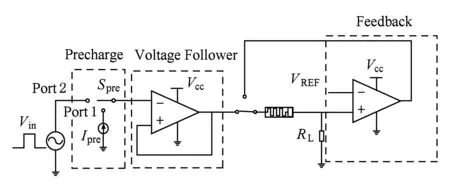
Fig. 10 The write circuit with feedback and precharge circuit图10 带反馈回路和预充电电路的写电路

图11所示的是使用预充电策略的写电路仿真结果，其相对误差为1.36%.

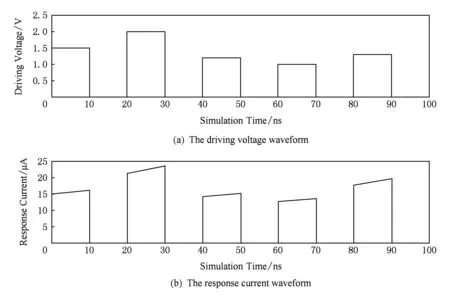
Fig. 11 The write process simulation results图11 写入过程仿真结果

4.3 噪声感知的训练方法

θo是来自其他来源的噪声，包括但不限于器件电子噪声和过程噪声等.器件电子噪声来自于电路器件本身，包括热噪声和闪烁噪声等；过程噪声来自于电路工作中的各种随机变化.θo成分都是随机过程量，通常用统计模型来表示，并且，成分难以通过优化电路设计的方法来抑制消除.

本文提出了一种噪声感知的训练方法，能够将这部分无法靠优化电路消除的噪声成分在线下训练时抵消掉.文献[17]中提供了MOS晶体管的噪声模型，文献[18]中提供了忆阻器的噪声模型，过程噪声可以使用正态分布来建立模型.确立了噪声的统计模型之后，需要将每一个权重经过的电路路径上的所有噪声分量进行叠加，详细的公式推导请参阅参考文献[17-18].在进行线下训练时，根据神经网络应用的规模和深度确定模型参数，将这些噪声分量模型注入到原本的训练过程中，使得权值得到调整.通过这种方式，能够将识别准确率提高3%左右.

5 实验与结果分析

5.1 仿真平台与配置

电路的仿真平台为HSPICE，使用到的基本电路元件有：电阻、电容、NMOS晶体管、PMOS晶体管和模拟忆阻器等.

电阻和电容使用HSPICE基本元件库中的模型；NMOS晶体管和PMOS晶体管使用文献[19]中的0.13um工艺模型，该工艺库中有2种规格的MOS管，分别为驱动电压1.5 V和驱动电压3.3 V，本文选择3.3 V规格.

忆阻器使用文献[20]的Spice模型，将其参数按照表2设置.其中，ROFF代表最大阻值，RON代表最小阻值，RINT代表初始阻值，D代表忆阻器薄膜厚度，μv代表迁移速度，p代表窗口函数的参数.

Table 2 Memristor Parameter Setting表2 忆阻器参数设置

5.2 仿真基准的选择

本文选择了3类6种基准，包括2种不同规模的28×28输入卷积神经网络、3种不同规模的多层感知器(MLP)和1种VGG-19网络，前2类被广泛运用于MNIST手写体识别，VGG-19运用于RGB图像识别.表3～表5分别给出了仿真基准的所有参数[21].

多层感知器是神经网络中较简单的一种，含有一个输入层、一个输出层和若干个隐藏层.隐藏层进行的是乘累加运算，比起卷积神经网络往往深度和复杂度较低.事实上，卷积神经网络是多层感知器的一种特殊化，是将多层感知器中的隐藏层特定为卷积和降采样操作的结果.VGG-19网络是一种规模较大的多通道神经网络.神经网络的规模大小和深度会直接影响本文所设计的电路结构的加速和节省能耗的效果.因此这里选择多种不同规模和深度的神经网络，以便分析各项性能与神经网络尺寸和深度的关系.

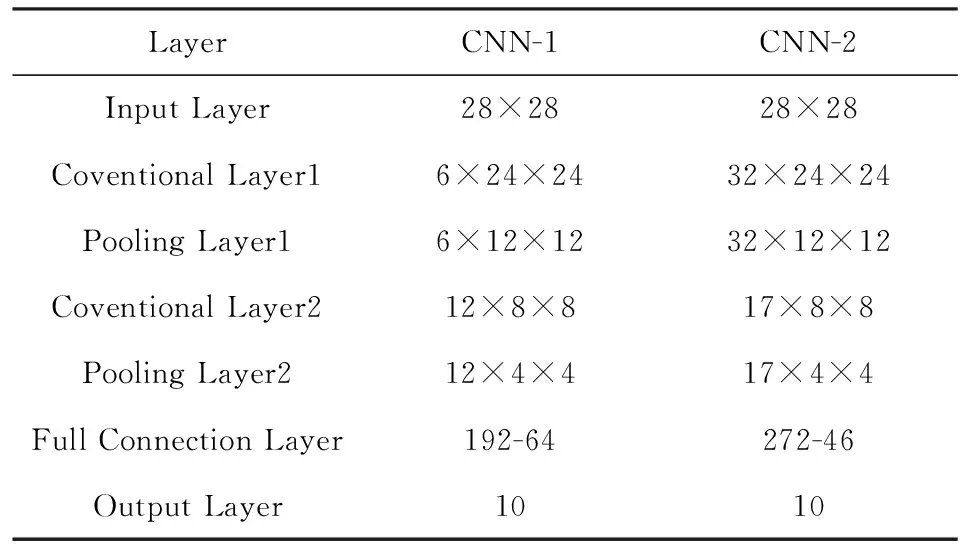
Table 3 Two Kinds of CNN Benchmarks Parameters表3 2种卷积神经网络仿真基准参数

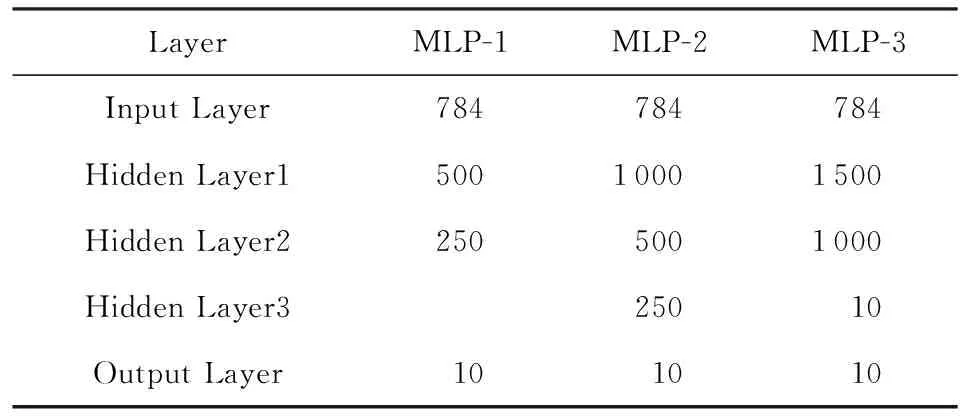
Table 4 Three Kinds of MLP Benchmarks Parameters表4 3种多层感知器仿真基准参数

Table 5 VGG-19 Benchmarks Parameters表5 VGG-19网络仿真基准参数

5.3 仿真结果与评估分析

文献[3]中提出了一种基于数字忆阻器的神经网络PIM结构，与本文相比主要有以下3点不同：

1) 使用的忆阻器模型不同.文献[3]中的所有忆阻器都采用数字忆阻器模型，这对数模/模数转换器提出了更高要求，引入了大量转换单元，进而造成大量的功耗和面积消耗.而本文中的设计采用模拟忆阻器模型，只在bank的输入输出接口需要使用数模/模数转换单元，可以节省数模/模数转换带来的额外消耗.同时，数字忆阻器的数据密度低于模拟忆阻器，文献[3]中使用8个忆阻器存储一个权重数据，每读写一次数据需要对8个忆阻单元进行读写，而本文的设计使用1个忆阻器存储一个权重数据，节省了7/8的存储面积消耗和读写功耗.

2) 从卷积神经网络到阵列的映射方法不同.本文提出的设计将一次卷积运算拆解为横向和纵向2个方向，在2个阵列中分别计算，并且将权重阵列展开错位放置，使得计算得以加速.

3) 噪声敏感度不同.文献[3]中的数字忆阻器对噪声敏感度较低，噪声需要积累一定量才会使得忆阻器的状态发生错误改变.而本文中的设计采用模拟忆阻器，对噪声敏感度高，少量的噪声积累就可能发生错误的结果，因此第4节中提出了一些适应于模拟电路的噪声消除方法.

下面将利用HSPICE平台，根据6种不同的Benchmark分别搭建电路系统，从图像识别准确率、能耗和性能这3个方面分别对以上本文和文献[3]中的设计进行仿真并比较和分析仿真结果.

图12为图像识别准确率的仿真结果.5组柱状图中的每一组代表一种神经网络仿真基准，假设使用Matlab进行浮点运算所得的该神经网络识别准确率为单位1.每组的柱体1(Before Adjust)代表使用本文设计的系统，但不采用任何噪声消除措施的准确率；柱体2(After Adjust)代表使用本文设计的系统，采用第4节所有噪声消除措施的准确率；柱体3(Design of Ref[3])代表文献[3]中的数字忆阻器系统的准确率.折线上的点(Accuracy Improvement)代表经过噪声消除措施后准确率的提高量.

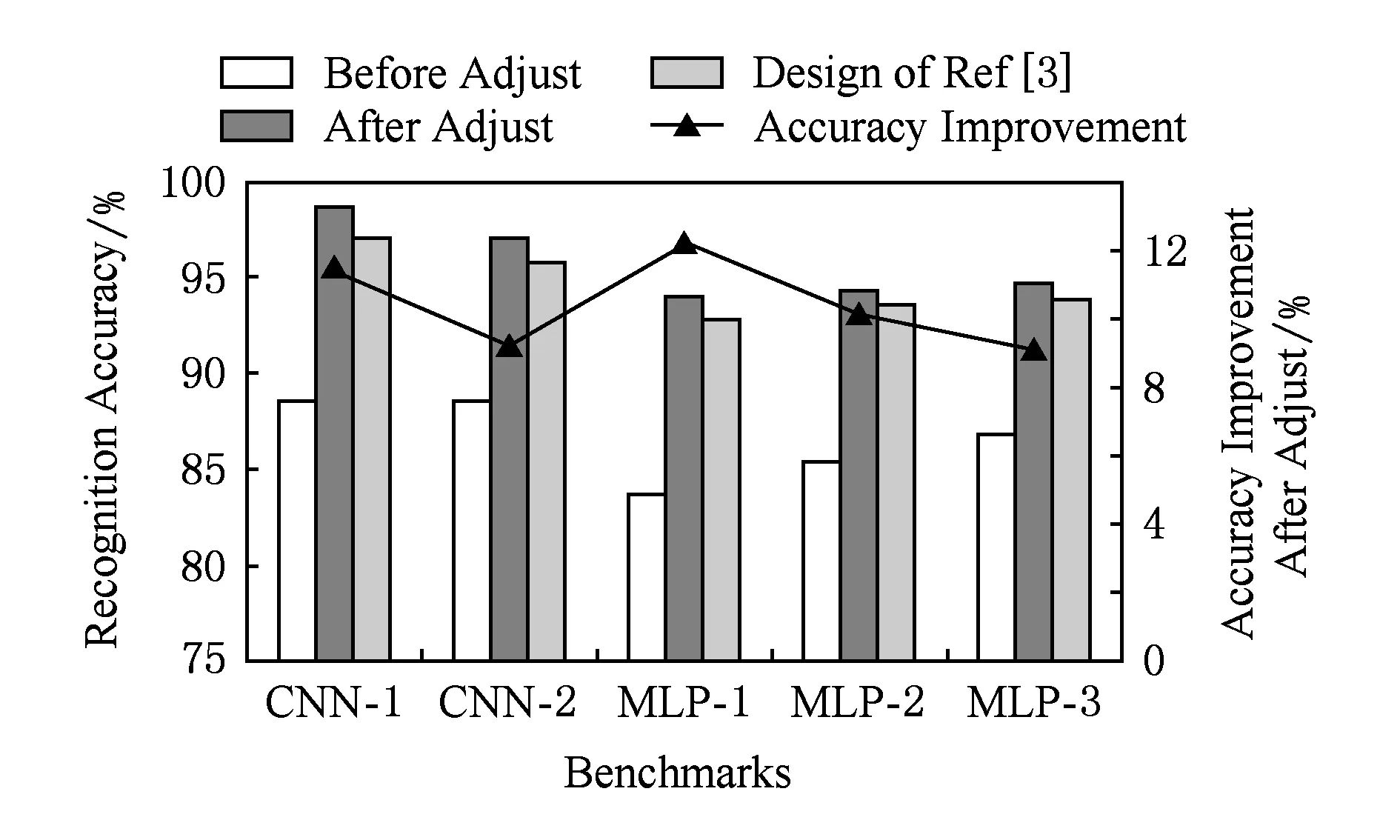
Fig. 12 Simulation results of recognition accuracy图12 图像识别准确率仿真结果

由图12的仿真结果可以看出：

1) 文献[3]中的数字忆阻器系统的准确率在95%左右，文本所设计的模拟系统如果不使用任何噪声消除措施，将会比数字系统降低8%左右的准确率，这是由于模拟电路对噪声的高度敏感性.而采用了第4节介绍的所有噪声消除措施之后，准确率可以比噪声消除前提高10%左右，比数字系统的准确度略高一些，是可以接受的识别准确率.

2) 每组测试基准中，本文设计的系统与数字系统的准确率差异相差不大，与测试基准的规模、深度并没有明显的关系.

图13为能耗节省量的仿真结果.6组柱状图中的每一组代表1种神经网络仿真基准，每组中柱体1(Design of Ref[3])代表文献[3]中的数字忆阻器系统的能耗；柱体2(Proposed Design)代表本文设计的系统的能耗.折线上的点(Energy Saving)代表本文设计的系统相对于数字系统的能耗节省比.

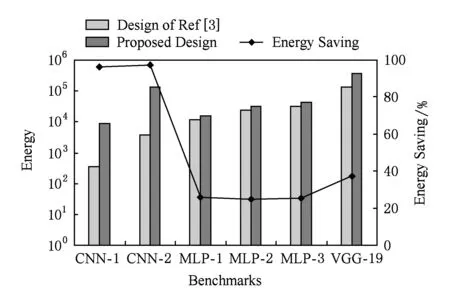
Fig. 13 Simulation results of energy saving图13 能耗优化仿真结果

正如1.2节所分析的，本文设计的系统拥有比数字系统更低的能耗，节省的能耗主要包括：1)在数模/模数转换模块上的额外功耗；2)在进行多位读写时消耗的额外能耗.

从图13的仿真结果可以看出：

1) 对于6层的CNN，如CNN-1和CNN-2，本文设计的系统能够节省超过95%的能耗.

2) 对于MLP，本文设计的系统能够节省超过24%的能耗.

3)对于VGG-19，本文设计的系统能够节省40%的能耗.

4) 综合上面3条结论，可以发现当神经网络的规模和深度增加时，能耗的节省量也随之增加.这是因为在大型网络中具有更多数模/模数转换模块，也需要更多次数的多位读写，能够被优化的能耗占比随着规模和深度增加而快速增长.而VGG-19的网络结构较为特殊，多个卷积层相连，而降采样层数量少，因此取得的效果低于CNN.

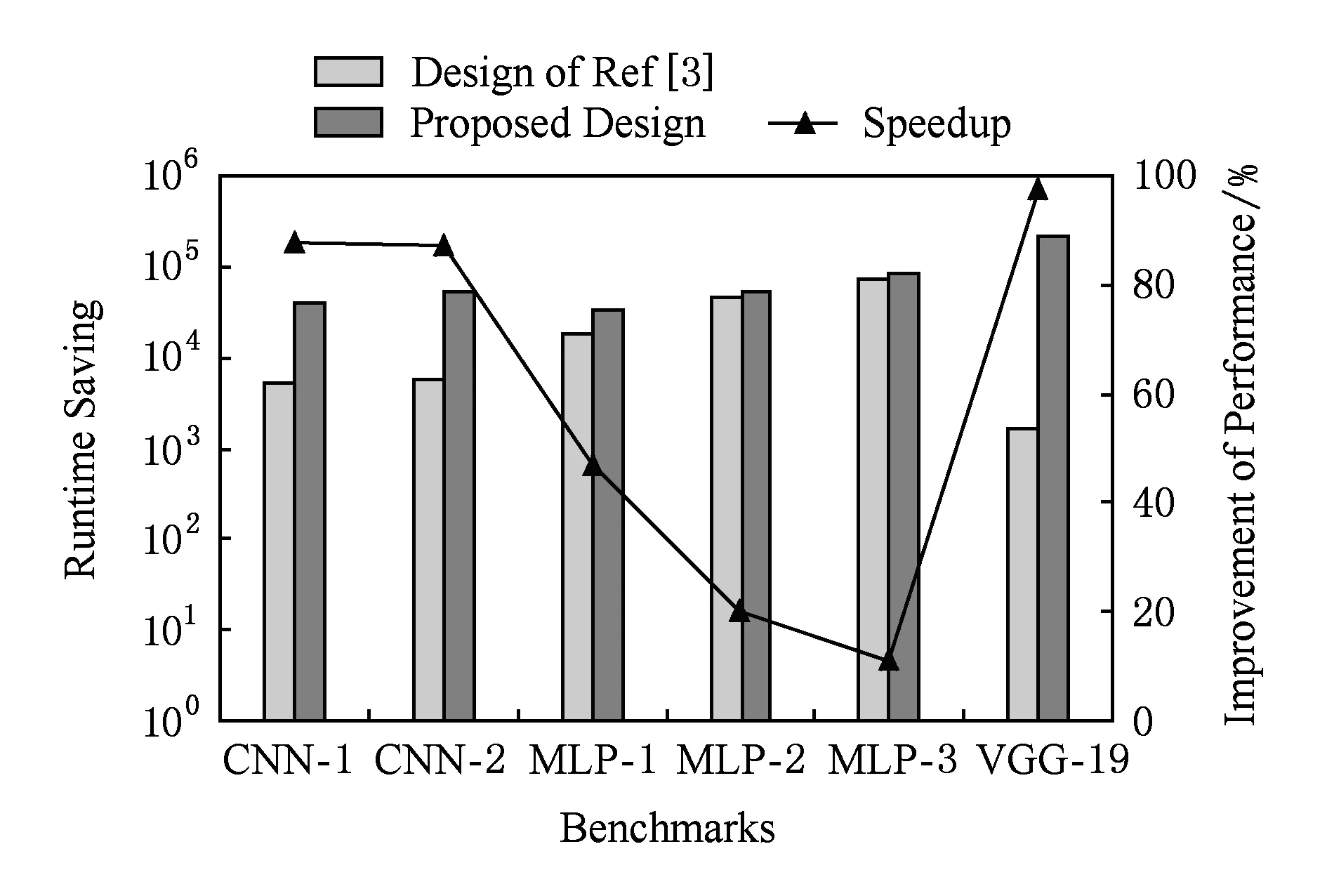
Fig. 14 Simulation results of performance improvement图14 性能提升仿真结果

图14为性能提升量的仿真结果.5组柱状图中的每一组代表一种神经网络仿真基准.每组中的柱体1(Design of Ref[3])代表文献[3]中的数字忆阻器系统的执行时间；柱体2(Proposed Design)代表本文设计的电路的执行时间.折线上的点(Speedup)代表本文设计的系统相对于数字系统的性能提升比.

性能提升主要得益于WSA中将权值展开错位放置的策略.假设输入图大小是n×n,卷积核的大小是k×k，滑步是l，该策略能够将原本需要(n-k+l)l×k个周期的一层卷积层运算缩减到n个周期内.

从图14的仿真结果可以看出：

1) 对于6层的CNN，如CNN-1和CNN-2，本文设计的系统能够节省超过90%的运行时间.

2) 对于MLP，本文设计的系统能够节省22%～47%的运行时间.

3) 对于VGG-19，本文设计的系统能够节省超过98%的运行时间.

4) 综合上面3条结论，可以发现当神经网络的规模和深度增加时，运行时间的节省量也随之增加.这是因为当层的规模越大时，每层节省的周期数占比越大；同时，当层的数量越多时，节省的周期数累积占比越多.

6 结 论

此前，基于忆阻器的神经形态近似计算的PIM结构中存在面积和能耗浪费，本文设计了新型的基于忆阻器的PIM结构实现深度卷积神经网络近似计算，选择模拟忆阻器来减少数模/模数转换次数，改变忆阻器阵列的组织方式来增加数据并行性，并针对该结构中可能存在的精度损失给出了相应的优化策略.本文选取6种不同规模和深度的神经网络，在HSPICE平台上进行了仿真.实验结果表明，本文所设计的结构在准确度不下降的前提下，在能耗和执行时间上都有明显优势.

[1]Hamdioui S, Xie L, Nguyen H A D, et al. Memristor based computation-in-memory architecture for data-intensive applications[C] //Proc of the 2015 Design, Automation & Test in Europe Conf & Exhibition (DATE’15). Piscataway, NJ: IEEE, 2015: 1718-1725

[2]Jo S H, Chang T, Ebong I, et al. Nanoscale memristor device as synapse in neuromorphic systems[J]. Nano Letters, 2010, 10(4): 1297-1301

[3]Chi Ping, Li Shuangchen, Xu Cong, et al. PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 27-39

[4]Liu Chenchen, Yan Bonan, Yang Chaofei, et al. A spiking neuromorphic design with resistive crossbar[C] //Proc of the 52nd ACM/EDAC/IEEE Design Automation Conf. New York: ACM, 2015: 1-6. Article No.14, DOI:10.1145/2744769.2744783

[5]Duan Shukai, Hu Xiaofang, Dong Zhekang, et al. Memristor-based cellular nonlinear/neural network: Design, analysis, and applications[J]. IEEE Trans on Neural Networks & Learning Systems, 2015, 26(6): 1202-1213

[6]Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C] //Proc of the 25th Int Conf on Neural Information Processing Systems. New York: Curran Associates Inc, 2012: 1097-1105

[7]Zhang Lei, Zhang Yi. Big data analysis by infinite deep neural networks[J]. Journal of Computer Research and Development, 2016, 53(1): 68-79 (in Chinese)

(张蕾, 章毅. 大数据分析的无限深度神经网络方法[J]. 计算机研究与发展, 2016, 53(1): 68-79)

[8]Williams R S. How we found the missing memristor[J]. IEEE Spectrum, 2008, 45(12): 28-35

[9]Tang Tianqi, Xia Lixue, Li Boxun, et al. Spiking neural network with RRAM: Can we use it for real-world application?[C] //Proc of 2015 Design, Automation & Test in Europe Conf & Exhibition. Piscataway, NJ: IEEE, 2015: 860-865

[10]Wang Ying, Zhang Lei, Han Yinhe, et al. ProPRAM: Exploiting the transparent logic resources in non-volatile memory for near data computing[C] //Proc of the 52nd IEEE/ACM Design, Automation Conf. Piscataway, NJ: IEEE, 2015: 1-6. Article No.47, DOI: 10.1145/2744769.2744897

[11]Wang Ying, Xu Jie, Han Yinhe, et al. Deep Burning: Automatic generation of FPGA-based learning accelerators for the neural network family[C] //Proc of the 53rd IEEE/ACM Design, Automation Conf. Piscataway, NJ: IEEE, 2016: 1-6. Article No.110, DOI: 10.1145/2897937.2898002

[12]Wang Ying, Li Huawei, Li Xiaowei, Rearchitecting the on-chip memory subsystem of machine learning accelerator for embedded devices[C] //Proc of 2016 IEEE/ACM Int Conf on Computer Aided Design. Piscataway, NJ: IEEE, 2016: 1-6. Article No.13, DOI: 10.1145/2966986.2967068

[13]Lécun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324

[14]Manem H, Rose G, He Xiaoli, et al. Design considerations for variation tolerant multilevel CMOS/NANO memristor memory[C] //Proc of ACM Great Lakes Symp on VlSI 2009. New York: ACM, 2010: 287-292

[15]Byeon D S, Yoon C W, Park H K, et al. Disturbance-suppressed ReRAM write algorithm for high-capacity and high-performance memory[C] //Proc of the 14th Non-Volatile Memory Technology Symp. Piscataway, NJ: IEEE, 2014: 1-4. DOI: 10.1109/NVMTS.2014.7060837

[16]Huang G M, Ho Yenpo, Li Peng. Memristor system properties and its design applications to circuits such as nonvolatile memristor memories[C] //Proc of 2010 Int Conf on Communications, Circuits and Systems. Piscataway, NJ: IEEE, 2010: 805-810

[17]Archanaa M, Balamurugan K. Analysis of thermal noise and noise reduction in CMOS device[C] //Proc of 2014 Int Conf on Green Computing Communication and Electrical Engineering. Piscataway, NJ: IEEE, 2014: 1-5. DOI: 10.1109/ICGCCEE.2014.6922246

[18]Georgiou P S, Koymen I, Drakakis E M. Noise properties of ideal memristors[C] //Proc of 2015 IEEE Int Symp on Circuits and Systems. Piscataway, NJ: IEEE, 2015: 1146-1149

[19]Yang M T, Ho P P C, Lin C K, et al. BSIM4 high-frequency model verification for 0. 13 μm RF-CMOS technology[C] //Proc of 2004 IEEE MTT-S Int Microwave Symp Digest. Piscataway, NJ: IEEE, 2004: 1049-1052

[20]Biolek Z, Biolek D, Biolkova V. SPICE model of memristor with nonlinear dopant drift[J]. Radioengineering, 2009, 18(2): 210-214

[21]Kussul E M, Baidyk T N, Nd W D, et al. Permutation coding technique for image recognition systems[J]. IEEE Trans on Neural Networks, 2006, 17(6): 1566-1579

Li Chuxi, born in 1991. PhD candidate of Northwestern Polytechnical University. Student member of CCF. Her main research interests include computer architecture and neuromorphic architecture.

Fan Xiaoya, born in 1963. PhD, professor, PhD supervisor. Senior member of CCF. His main research interests include computer architecture, machine learning, neuromorphic architecture and very large scale integrated circuit design (VLSI).

Zhao Changhe, born in 1994. Master candidate of Northwestern Polytechnical University. His main research interests include computer architecture and neuromorphic architecture.

Zhang Shengbing, born in 1968. PhD, professor, PhD supervisor. Senior member of CCF. His main research interests include computer architecture, machine learning, neuromorphic architecture and microelectronic circuit design.

Wang Danghui, born in 1975. PhD, associate professor. Member of CCF. His main research interests include computer architecture, emerging memory, neuro-morphic architecture and very large scale integrated circuit design (VLSI).

An Jianfeng, born in 1977. PhD, associate professor. Member of CCF. His main research interests include computer architecture, advanced micro architecture and reconfigurable computing.

Zhang Meng, born in 1978. PhD, assistant professor. Member of CCF. His main research interests include computer archi-tecture, machine learning, neuromorphic architecture and very large scale integrated circuit design (VLSI).

A Memristor-Based Processing -in -Memory Architecture for Deep Convolutional Neural Networks Approximate Computation

Li Chuxi1, Fan Xiaoya1,2, Zhao Changhe1, Zhang Shengbing1,2, Wang Danghui1,2, An Jianfeng1,2, and Zhang Meng1,2

1(SchoolofComputerScience,NorthwesternPolytechnicalUniversity,Xi’an710129)2(EngineeringandResearchCenterofEmbeddedSystemsIntegration(NorthwesternPolytechnicalUniversity),MinistryofEducation,Xi’an710129)

Memristor is one of the most promising candidates to build processing-in-memory (PIM) structures. The memristor-based PIM with digital or multi-level memristors has been proposed for neuromorphic computing. The essential frequent AD/DA converting and intermediate memory in these structures leads to significant energy and area overhead. To address this issue, a memristor-based PIM architecture for deep convolutional neural network (CNN) is proposed in this work. It exploits the analog architecture to eliminate data converting in neuron layer banks, each of which consists of two special modules named weight sub-arrays (WSAs) and accumulate sub-arrays (ASAs). The partial sums of neuron inputs are generated in WSAs concurrently and are written into ASAs continuously, in which the results are computed finally. The noise in proposed analog style architecture is analyzed quantitatively in both model and circuit levels, and a synthetic solution is presented to suppress the noise, which calibrates the non-linear distortion of weight with a corrective function, pre-charges the write module to reduce the parasitic effects, and eliminates noise with a modified noise-aware training. The proposed design has been evaluated by varying neural network benchmarks, in which the results show that the energy efficiency and performance can both be improved about 90% in specific neural network without accuracy losses compared with digital solutions.

memristor; processing-in-memory (PIM); convolutional neural network (CNN); approximate computation; analog memory

2017-02-27；

2017-04-14

国家自然科学基金项目(61472322)；中央高校基本科研业务费专项资金项目(3102015BJ(Ⅱ)ZS018) This work was supported by the National Natural Science Foundation of China (61472322), the Fundamental Research Funds for the Central Universities (3102015BJ(Ⅱ)ZS018).

王党辉(wangdh@nwpu.edu.cn)

TP303