采用流水化伪随机编码算法的相变存储器寿命延长方法

高 鹏 汪东升 王海霞

1(清华大学计算机科学与技术系 北京 100084)2(清华大学信息技术研究院 北京 100084)

采用流水化伪随机编码算法的相变存储器寿命延长方法

高 鹏1,2汪东升2王海霞2

1(清华大学计算机科学与技术系 北京 100084)2(清华大学信息技术研究院 北京 100084)

(gaopeng1982@gmail.com)

相变存储器(phase change memory, PCM)是一种颇具前景的新型存储器件，具有非易失性、静态功耗低和存储密度高的优点.然而，该类器件的低写入寿命是其在实用化中亟待克服的关键问题之一.一般来说，通过每次写入时仅写入相异位的策略，可以减少产生的平均写入量，从而延长PCM的写入寿命.然而，应用这一差异式的写入策略通常又会以降低读写速度为代价.为此，提出了一种兼具高效和快速特点的写入量减少方法FEBRE(a fast and efficient bit-flipping reduction technique to extend PCM lifetime).该方法在差分写入阶段前，设计并使用了一种快速的一对多映射，将待写入的数据并行映射为多个编码向量，从而增加了从其中找到一个与已有数据最近的向量的可能性.此外，还提出了一种流水化的伪随机编码算法，用以加速一对多映射中的编码过程，从而降低写入开销.实验表明，与目前领先的PRES(pseudo-random encoding scheme)方法相比，FEBRE方法在写入操作中，平均减少了5%以上的写入量，提升了2倍以上的编码速度；在读取操作中，减少了45%以上的解码操作次数.

相变存储器件；差分写入；伪随机编码算法；编码方向模式；星型生成规则

随着软硬件技术的发展，现代计算机系统对高速、大容量、低功耗的内存系统产生了越来越迫切的需求.然而，目前广泛使用的DRAM(dynamic random access memory)存储器件,已经越来越接近其性能发展的极限[1]，这是由该技术自身的漏电功耗和存储密度所造成的.为了进一步提升存储系统的性能和容量，同时降低系统功耗，工业界和学术界目前都在积极探索构成下一代存储系统的相关方案.其中最具代表性的技术就是相变存储器(phase change memory, PCM)[1].相比于目前广泛使用的DRAM器件，PCM器件具有静态功耗低、随机读写速度高和容量密度大(4倍于DRAM)等诸多优点[1-3]，因此也被视为是构建未来存储系统的重要选择之一.

然而，PCM技术也存在一个亟待克服的缺点，即由破坏性的写入行为所致的较短的写入寿命(写入寿命一般被定义为存储单元的翻转次数上限.PCM的写入寿命一般为106～109次，而DRAM器件一般不低于1014次[1-2]).有研究表明[4]，在极端条件下，如不采取任何缓解写入磨损的措施，一个精心设计的写入序列可以在数分钟内用完一个全新PCM单元的全部写入寿命，并导致其失去存储能力而出现故障.因此，延长写入寿命是PCM技术得以广泛使用的前提之一.

差分写入策略是一种有效的PCM写入寿命延长方法[5-6].其核心思想在于把待写入数据通过某种编码算法映射为多个不同的编码向量，然后从中找出一个和已有数据相异位数最少的向量.通过仅写入与已存储数据相异的位来完成写入，该类方法[5-10]可以有效地降低每次写入时的写入量.但是，此类方法一般也面临效率和执行速度的矛盾：简单编码算法执行速度较快，却难以取得较好的写入量减少效果；而复杂的编码算法通常又会带来读写速度的降低，进而影响系统性能.

为了达到较好的写入量减少效果，且保持较低的读写代价，本文提出了一种快速而高效的差分式写入量减少方法FEBRE(a fast and efficient bit-flipping reduction technique to extend PCM lifetime).该方法通过将带写入的数据映射为多个随机化的编码向量，提高了从这些编码向量中找到一个与目标地址已有数据更加相似的向量的概率，从而减少了写入时的差异位数，最终降低了写入量.

该方法的核心之处在于其采用了一种新颖的编码向量并行生成和组织方法，称为星型生成规则.该规则中，多个随机化分布的编码向量由一个待写入的数据通过一个并行映射而来.首先，在这一规则中，待写入数据采用了一对一的直接生成方式产生编码向量.这一方式消除了之前方法中编码向量间的重复问题，从而进一步提升了在编码向量集合中找到一个与存储数据更近向量的概率，进而降低每次写入的平均写入量.其次，星型生成规则还可以通过减少编码/解码的次数来加快读写速度.此外，本文设计了一种流水化的伪随机编码算法，不仅对输入数据保持了较高的随机化能力，而且加速了编码向量生成步骤中的编码速度，缓解了其对读写速度带来的影响.

实验证明，以上这些创新带来的优势使得FEBRE方法具有更快的读写速度和更好的写入量减少效果.与目前领先的PRES方法相比，FEBRE方法在写入操作中平均减少了5%以上的写入量，提升了2倍以上的编码速度；在读取操作中，减少了45%以上的解码操作次数.

1 相关工作

在其他条件相同的情况下，对于某个PCM存储单元而言，越少的写入量就意味着越长的写入寿命，这就是差分式写入方法的基本思想.而以下所述的各方法正是遵循这一思路逐步发展而来的，其共同点是通过将待写入的数据变换为与已有的数据更加相似的形式，从而达到更好的写入量减少效果.

作为此类方法中最简单的形式，Data Compare Writing(DCW)[5]方法仅使用待写入数据作为唯一的候选项与已有数据进行比较.Flip-N-Write(FNW)[6]在DCW的基础上，提供了待写入数据和其逐位取反的结果作为2个候选项，并将两者中写入代价较小的那一个用于最终写入.Min-Shift[7]方法在FNW方法的基础上，通过对待写入数据添加位移操作，产生了更多的候选数据项.总而言之，尽管这些方法带来的读写操作代价较低，但其写入量减少能力也相对较弱.

一般来说，将一个待写入数据变换为多个随机化的编码向量后，可以从中找出一个向量，并使得被选出的向量比待写入数据更接近已有数据.而且，更多的编码向量会进一步提高被选出的向量与已有数据的相似性，因而也会带来更好的写入量减少效果.

基于这一思想，近期该领域的研究在进行数据比较前增加了一个显式的一对多映射的步骤，用以将一个待写入数据编码为多个编码结果，并将其作为待比较的数据向量.Flip-Min[8]是该思路的代表方案之一，通过使用Hamming纠错编码，Flip-Min中将待写入数据编码为多个带有随机错误但又是可被纠错的编码向量.而作为最接近本文的研究，PRES(pseudo-random encoding scheme)[9-10]方法中的一对多映射被分割为前后相继的2个部分：一种数据变换策略，用以生成待写入数据的多个带有不同子数据划分模式的副本；随后的一对一映射，负责对划分后的子数据进行编码，从而将数据副本映射为多个不同的随机化编码向量.总之，PRES方法提出的随机化一对多映射使其超过了其他所有同类方法的写入量减少效果.

尽管PRES方法被认为具有目前最好的写入量减少效果，但是本文经过分析发现该方法仍然存在2个问题：1)该方法产生的编码向量集合中存在相当多的重复元素；2)较慢的编码算法和编码向量生成方式.这些问题不仅降低了写入量减少的效果，而且拖慢了读写速度.

2 研究动机

PRES是目前领先的差分式写入方法，但其也存在一些问题.为了继承该方法的优秀部分，并摒弃其中的不利因素，本节将首先深入分析PRES方法存在的问题及其成因，以期在其基础上提出一种更加高效和快速的方法.

2.1 重复元素起因分析

PRES产生的编码向量集合中存在大量的重复元素，这将直接降低其写入量的减少效果.这是该方法最大的问题，同时也是被其后来研究所忽视的一点.为了探索这一问题的成因，本节将首先介绍PRES中定义的一些概念，并回顾PRES中生产一个典型编码向量的过程，以期从中找出问题的根源.

编码方向模式是PRES引入的一个概念，用于描述一个数据是如何被从形式上划分为多个子数据的，以及规定划分后的每个子数据段中各个位的编码顺序.例如，一个二维矩阵化排列的数据可以被划分为多个行向量的集合，并按照从左到右的方式逐位访问,而此时的这种划分和访问方式就被定义为一种编码方向模式.

PRES中存在2种编码向量:1)仅通过一次编码待写入数据而产生的，称为一次编码向量,这部分向量仅占全部向量数的很少一部分;2)将第1种编码向量作为输入，并采用与之不同的编码方向模式进行再次编码而产生的，称为二次编码向量.但是，在PRES给出的例子中，本文发现，有一半的二次编码向量，其内容是完全重复的.尽管这些编码向量应用的是不同的编码方向模式序列.究其原因，本文认为是由于多次编码产生方式，以及编码方向模式之间的可交换性所造成的.

编码方向模式的可交换性是指在上述的生成二次编码向量的过程中，某些编码方向模式的使用顺序可以被交换而不影响最终的编码结果.为了展示这一结论，我们首先考虑一个典型的2次编码过程.即先使用Left-to-Right(LR)模式编码一个数据，然后再使用Top-to-Bottom(TB)模式来编码第1步产生的结果.最终产生的二次编码向量中的任一位可按如下公式计算得出：

(1)

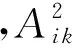
由上述可知，编码向量集合中的重复元素问题可以被归因于编码方向模式的可交换性和多次编码的工作方式.而这一点并未被之前的研究所注意到.此外，已有研究也已经证明，编码向量集合的随机性和写入量减少是呈正相关的[8-10].因此，编码向量集合中的重复元素会直接降低该集合的随机性，进而降低了该方法的写入减少效果.

2.2 读写速度分析

PRES存在的另一个问题是读写速度缓慢.而本文认为这也是因为其采用了层次式的编码向量生成和组织方式所造成的.具体而言，PRES中的编码向量的生成过程如图1所示：待写入的数据首先被排列为二维矩阵(不改变内容)，然后按照水平或垂直方向划分为多个行向量或列向量.之后，对划分出的这些向量按照从左到右或从上到下的方向逐位编码，从而生成一级编码向量，继续重复这一过程可以形成二级编码向量.因此，相对于一次生成所有编码向量的方法，如Flip-Min，这一过程无疑会带来更多的写入时间.

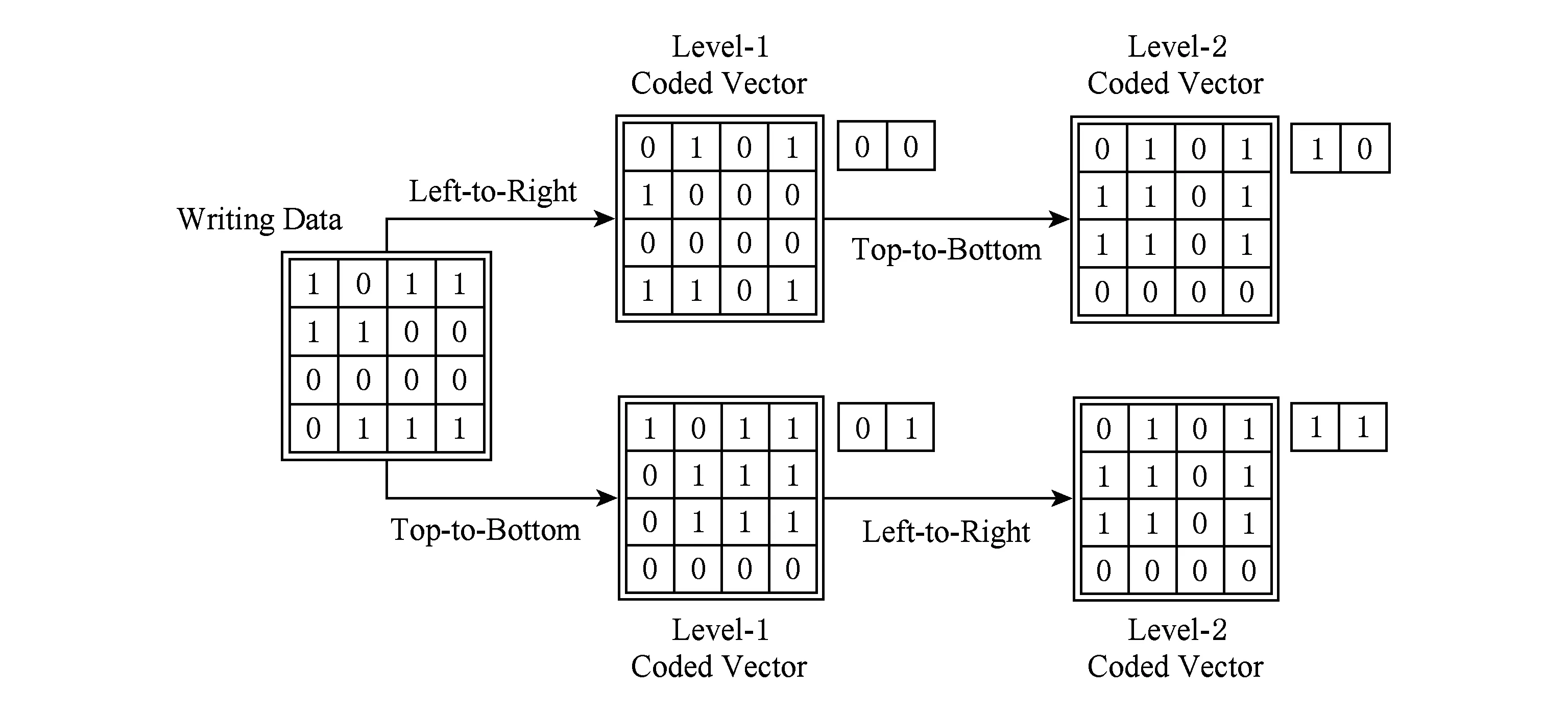
Fig. 1 Generating level-1 and level-2 coded vectors in PRES (2 coding direction patterns are used for 4 coded vectors)图1 PRES方法中一/二级编码向量的生成方式(采用2个编码方向模式产生4个编码向量)

而对于读取操作，那些经过2次编码而产生的向量同样需要2次解码才能得到写入的数据，而且需要2次解码的向量占据了整个编码向量集合的绝大部分.因此，这种方式下的读取速度也会因此而受到影响.

此外，PRES中所用到的伪随机编码算法是一个串行过程，待编码数据的各个位需要依次被编码.而这又会延长编码时间，进一步降低写入速度.以下是该算法的形式化表达

P1=B0+B1；
Pi=Pi-1+Bi；
P0=BL-1+B0.

(2)

B0=PL-1+P0；
B1=P1+B0；
Bi=Pi-1+Pi.

(3)

其中，i=1,2,…,L-1,L为输入数据的长度；Bi表示输入数据的位;Pi表示编码结果的位.

尽管式(2)具有较好的数据随机化能力，但其逐位进行编码的工作方式决定了K位长的数据编码过程至少需要K级加法延迟.这一过程对于长度较长的数据而言将耗费更多的时间.

3 FEBRE方法

3.1 基本思想

本文所述的FEBRE方法是建立在PRES方法之上，并针对其缺点进行改进而提出的一种方法.FEBRE的核心思想在于如何构造一对多映射，而这也是该方法与其他所有类似方法最大的不同之处.因此，本节将沿着构造一对多映射的顺序来介绍FEBRE方法.

在FEBRE方法中，一对多映射被分为了数据划分和子数据段编码2个前后相继的阶段：

阶段1. 由星形生成规则和广义编码方向模式共同构成，用以将输入数据变形为多种形态，但保持内容不变；

阶段2. 由流水化伪随机编码算法构成，用以将第1阶段生成的数据变换为多个随机分布的编码向量.

在数据分划阶段，待写入的数据将首先产生K个副本(K为系统定义的最大副本数量).然后，为每个数据副本配备唯一的一种预定义的编码方向模式，并将数据副本按照其自己的编码方向模式划分为多个子数据段.此时各数据副本之间的内容不变，仅是数据划分方式不同.在这一过程中，为每个数据副本指定一个唯一的编码方向模式的生成规则，在本文中被称为星型生成规则.

与PRES方法不同的是，本文中所用到的编码方向模式不再局限于水平/垂直等按照自然方向定义的划分方式上，而是被赋予了更广泛的含义，即由不同位构成的一个排列.因此这样的编码方向模式也被称为广义编码方向模式.

在编码阶段中，流水化伪随机编码算法将作为一对一映射被应用于划分出的每一个子数据段上，从而将原本相同的数据副本编码为不同的数据,由此产生的编码向量被称为候选向量.然后，目标地址上的已有数据将与每个候选向量分别进行比较，并选出具有最少相异位的那一个编码向量，用于最终写入.此外，产生该向量的编码方向模式的编号也将被一同记录，用于读取时的解码操作.通过仅翻转目标地址上那些与选出的向量不同的位，差分式写入最终得以完成.

FEBRE方法的读取过程相对简单.当目标地址上的数据，及写入时被记录的编码方向模式编号被读出后，该数据将被重新排列为二维矩阵.之后，根据读出的编码方向模式，该数据将被划分为多个子数据段.对每个子数据段应用式(3)所定义的伪随机解码算法，即可以得到解码后的数据，该数据即为写入时的原始数据.

3.2 星形生成规则

本文提出了一种新的编码向量集构造方法，称为星型生成规则,作为交叠使用编码方向模式的替代.该方法规定，每个编码向量必须由唯一的一个编码方向模式，仅经过一次编码而生成，各编码方向模式之间不可以重用.图2给出了使用星型生成规则生成4个编码向量的示意图.如图2所示，一个待写入数首先被复制多份，然后每个副本根据某一个选定的编码方向模式被划分为多个子数据块的组合，最后每个子数据块进行编码.而这些被编码过的数据副本无需进一步处理，就直接构成了所需的编码向量集合.

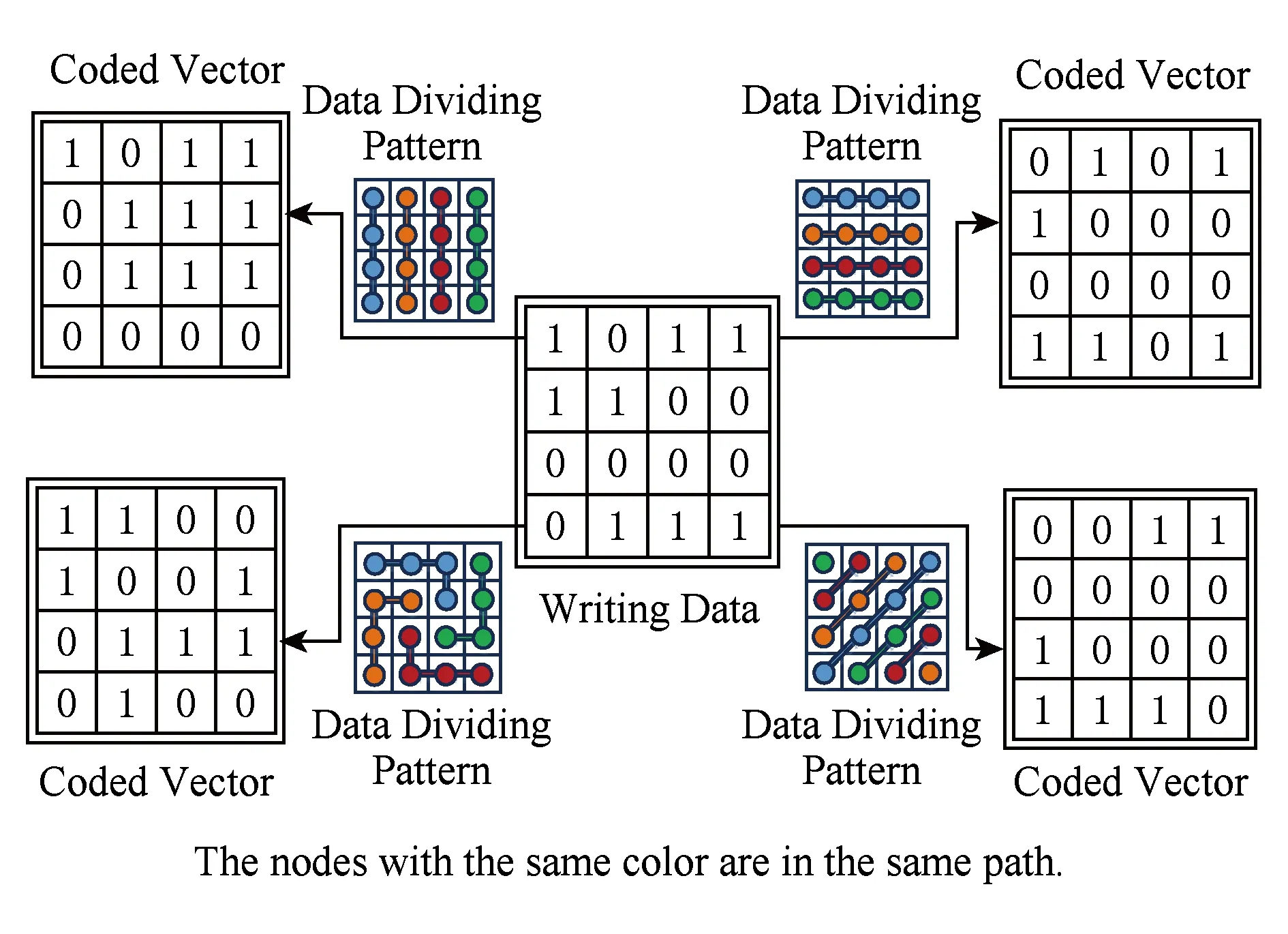
Fig. 2 Generating coded vectors with the star-rule (4 coding direction patterns are used for 4 coded vectors)图2 星型生成规则下的编码向量的生成方式(采用4个编码方向模式产生4个编码向量)

星型生成规则是一个简单但行之有效的规则.

1) 应用不同编码方向模式而产生的伪随机编码结果至少会存在一个位的不同，因此编码结果集合必然没有重复现象.而其直接结果就是带来更少的写入量.

2) 由于每个编码向量都可以独立地并行生成，没有相互依赖，因此编码速度得以提升，即写入时间更短.

3) 星型生成规则中的一次编码行为也意味着读取时仅需一次解码，即读取时间更少.

显而易见，星型生成规则需要更多的编码方向模式，而这是传统编码方向模式(水平、垂直、对角线)所不足以提供的.为了解决这一问题，本文将传统的编码方向模式扩展为广义编码方向模式.

3.3 广义编码方向模式

首先本文定义一个带有长度参数的概念：路径.一个长度为S的路径是指一个数据向量中的S个不同位的一个排列.也就是说，一个路径指明了哪些位应该被视为在同一组中，以及这些位编码时的访问顺序.在此定义之上，一个广义编码方向模式被定义为一组路径的集合，并且规定这些路径定义在同一个数据上，且满足长度相等、互不相交、共同覆盖数据的所有位.图3给出了一些广义编码方向模式的实例，为了简化描述，此处仅讨论那些可以被排列为形如K×K方阵的数据.2个划分方式相同，但子数据段访问顺序相反的编码方向模式，例如LR和RL，在此图中仅列出一个，并为每种模式指定一个编号.如图3中所示，在每个编码方向模式中，同色的节点表示该位置被划分到了同一个子数据段中，而每个节点的标号表示该子数据段进行编码时的位访问顺序.至此，编码方向模式的定义从简单的自然方向被推广到了数据中不同位置元素的排列.而相比于水平/垂直/主副对角线的划分方式，广义编码方向模式更加深刻地反映了编码方向模式的本质，而且其可能的数量也能够完全满足星型生成规则下对编码方向模式数量的需求.

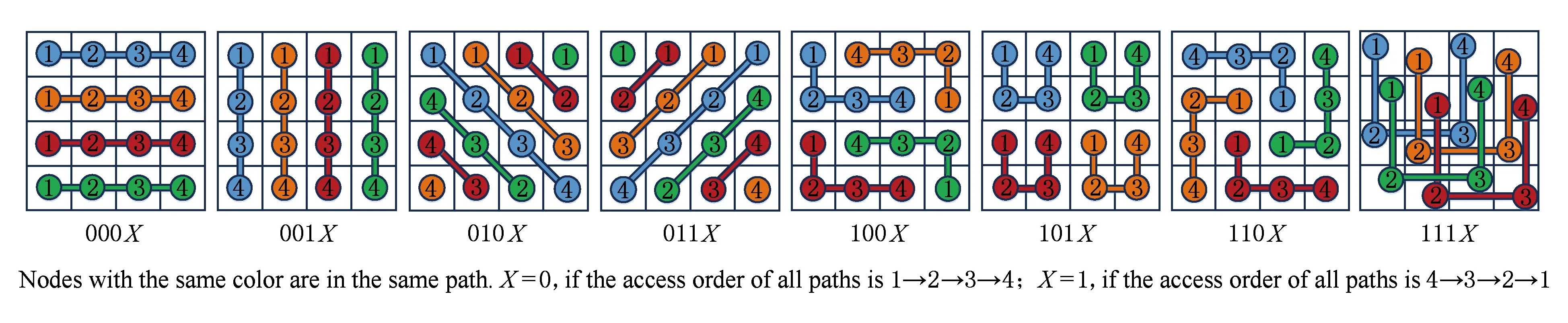
Fig. 3 Examples of the expended coding direction patterns and the index rule图3 扩展后的编码方向模式示例及其编号规则

3.4 流水化伪随机编码算法

在划分阶段之后，FEBRE方法将使用流水化伪随机编码算法(pipelined pseudo-random encoding algorithm, PPREA)对每个分划出的子数据段进行编码.通过这一步骤，内容相同的数据副本将被变换为不同的编码向量.相比于按照式(2)定义的原始伪随机编码算法而言，本文提出的流水化伪随机编码算法在保持原始算法较好的随机化能力基础上，大幅度提高了执行速度.

3.4.1 核心思想

由于伪随机编码算法是一个连续加法的过程，因此，受到超前进位加法的启发，本文发现数据中某个位的编码结果也可以通过额外的逻辑提前计算得出，而无需在编码运算中获得.此外，由式(2)也可得出推论：数据中任一子数据段的编码结果将被该数据段的前一位的编码结果所唯一确定.

由此，本文构造了一种基于分治思想的伪随机编码的算法实现.其核心思想是：将一个待写入的数据划分为多个无交叠的子数据段后，通过额外逻辑提前计算出这些子数据段的前一位的编码值，然后并行展开所有子数据段的编码过程.

3.4.2 形式化描述

为了形式化地描述和证明该算法，本节首先定义如下的一些术语.DK用于表示长度为K位的数据向量(从Bit0到BitK-1).假设DK被平均地分为M个不相交的数据段D1,D2,…，DM-1,DM.每个数据段包含S个位，S=K是数据段Di进行编码时的输入，一般是其前一位的编码结果，也被称为该数据段的输入进位.是数据段的最后一位的编码结果，被称为该数据段的输出进位(也是下一个数据段的输入进位).规定数据段D1起始于Bit1、终止于BitS，其输入进位为Bit0(按照编码规则，D1的输入是Bit0而不是Bit0的编码结果)，其输出进位是D2的输入进位.最后一个数据段的输出进位被回绕定义为Bit0的位置.此外，本文定义辅助函数Parity()，用来计算并返回从D1到Di-1中的1的奇偶性.定义辅助函数PREM()用于对输入进位为的Di数据段进行如式(2)所定义的标准伪随机编码过程.PPREA的伪代码如算法1所示.

算法1. PPREA算法伪代码.

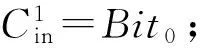
② Fori=1 toM

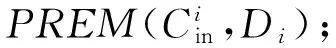
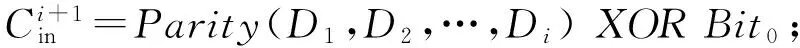
⑤ End FOR

3.4.3 正确性证明

为了证明算法1提出的算法的正确性，本文首先将提出一个引理，称为传播引理，并给出其证明.

传播引理. 当数据段中的某个子数据段进行伪随机编码时，该数据段的输入进位，该数据段中1的奇偶性(假设奇数为1，偶数为0)的异或(XOR)结果等于该数据段的输出进位.

证明：

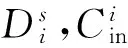
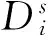
3) 考虑S=N+1的情况：

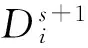
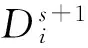
4) 综上，该引理对所有正整数N成立.

证毕.

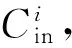
3.4.4 硬件实现

不同分段长度将给PPREA带来不同的实现代价.因此本节将讨论最优的分段长度选择及其硬件实现.

逻辑上，PPREA可以分为超前进位计算和数据段内编码2部分.对于一个S位长的子数据段而言，需要1+lbK个异或门延迟才能产生输出进位(作为下一个数据段的输入进位)，需要K-1个异或门延迟完成段内编码.因此，当且仅当1+lbK=K-1时，2部分电路不会出现相互等待的情况，可以充分发挥电路的并行性.即当子数据段长度为4时，达到最优分段.

图4给出了PPREA的最优电路实现，包括了4位和K(K>4)位输入数据的情况.虚线框中的电路负责产生每个数据分段的超前输入进位，其他门电路负责编码每个数据段内的位.为了节约资源，用于计算最后一个输入进位的电路在该实现中，也被借用于计算其他的输入进位.

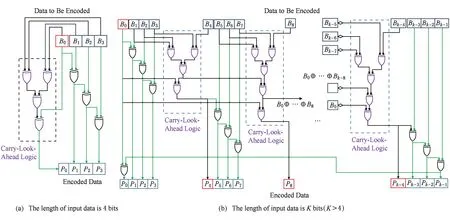
Fig. 4 The implementation of pipelined pseudo-random encoding algorithm with XOR gate图4 流水化伪随机编码算法的异或门实现

3.4.5 FEBRE方法的读写过程

至此，本文已经讨论了FEBRE方法中的各个组成要素：星型生成规则、广义方向模式以及流水化伪随机编码算法.为了更好地阐释FEBRE方法，本节将展示该方法的一个读写用例.如图5所示，值为0xBC07的数据将被写入一个内存位置，其值为0x7126，然后再读取该位置.系统可用的编码方向模式如图3所示，共计16个.系统读写字长为16 b.

写入过程首先产生待写入数据的16份副本;然后，这些副本将根据如图3所示的16个可用的编码方向模式被划分.在逻辑上，每个副本将被划分成4个子数据段，每个子数据段包含4 b.通过对每个子数据段应用PPREA，就可以得到16个不同的编码向量.之后，每个编码向量将会和目标地址已存储的数据0x7126进行比较.其中相异位数量最少的一个编码向量0x308E被选出，并写入那些相异位.同时，产生该向量所用的编码方向模式的编号0x7也被记录下来.

读取过程的第1步是读出已写入的数据0x308E和它的编号0x7;然后应用标号为0x7的编码方向模式，将0x308E重新划分为4个子数据段.在每个子数据段都应用了如式(3)所示的解码算法之后，就得到了最初写入的数据0xBC07.

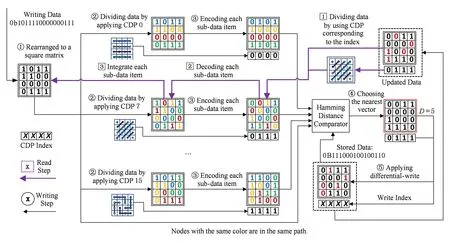
Fig. 5 Write/Read example for 16 b data图5 数据写入及读取过程示例(16 b)

4 性能评估

为了衡量本文提出方法的读写性能和写入量的减少能力，本节将着重测量以下参数：PPREA的执行速度和其实现代价、编码向量集合的生成速度，单个编码向量的解码速度和每次写入时的平均写入量.其中，速度和实现代价方面的测量结果将会与最为接近本文提出方法的PRES方法的结果进行对比；而每次写入时的平均写入量，作为该类方法最重要的性能参数，将与PRES,Flip-Min以及经典的Flip-N-Write方法进行对比,用以凸显FEBRE方法的优势.

4.1 测试方案及测试数据

除了Flip-N-Write方法，其他算法均难以进行数学建模[9]，因此本文将采用蒙特卡洛法进行测试，即：通过使用随机数据模拟对存储单元的写入和读取，来获得不同方法的写入时间、读取时间和实际写入位数等参数.具体而言，本文模拟了向一个初始值为0的存储单元连续写入108个随机产生的数据(数据长度包括了16 b，32 b，64 b，128 b，256 b，512 b和1 024 b这7种情形)的过程，每次写入后紧接着进行一次读取操作.此外，为方便测试，本文规定任何长度超过16 b的测试数据，都将按照多个16 b的基本组的组合形式进行处理.

4.2 测试配置

在模拟中，FEBRE使用了图3所列出的16个编码方向模式来产生相应的16个编码向量.作为对照组的PRES方法使用了其中的4个编码方向模式：Left-to-Right(LR),Right-to-Left(RL),Bottom-to-Top(BT)和Top-to-Bottom(TB).因此，PRES方法所产生的编码向量集将包括4个一次编码向量和12个二次编码向量.FEBRE方法使用了PPREA编码算法，而PRES采用的是非流水化的编码算法.此外，为了保证各方法之间的相对公平，本文规定每种方法的候选向量数保持一致.因此，参与对比的Flip-N-Write方法和Flip-Min均采用4 b标志位，对应16个候选向量.

4.3 PPREA实现的速度与代价分析

PPREA采用如图4所示的异或门结构实现.其执行速度、实现代价可以采用增量法来分析.首先假设数据段的长度K≫4且能被4整除，并用T来表示一个异或门产生的门延迟.当有4个新的位加入到已有数据段时，为了产生新的输出进位，该算法需要额外增加1T的门延迟，而段内编码时间则可以被完全隐藏，如图4(b)所示.此时的初始代价为5T，因此，对于K位的数据，PPREA需要(K4+5)T完成.例外情况是当K=4时，电路可简化为仅需要3T的时间，如图4(a)所示.作为对照，式(2)中定义的非流水化伪随机编码算法总是需要K×T的时间来产生同样的结果.因此，本文提出的流水化算法最大能够产生接近400%的加速比.

实现代价方面，本文仍采用增量法进行分析.当为已有的数据新加入4 b时，PPREA需要3个额外的异或门来对这些新加入的位进行编码、另外3个异或门完成奇偶性检测、2个额外的异或门来产生进位逻辑，总计需要8个异或门.推而广之，对长度为K的数据，PPREA需要2×K个异或门.例外情况是K=4时，仅需7个异或门.作为对比，对于长度为K的数据，非流水化的伪随机编码算法总是需要K个异或门.

4.4 编码向量集合生成速度对比

编码向量集合的生成过程是写入操作中最为复杂、关键的步骤.因此可以用该集合的生成速度作为评价写入速度的指标.图6给出了PRES和FEBRE 2种方法在这一指标上的归一化比较结果.对16/32 b数据，FEBRE方法取得了至少2.29倍的加速效果(速度定义为所需时间的倒数)，且加速比还会随字长的增加而进一步增加,这一加速效果是由PPREA和星型生成规则所共同带来的.

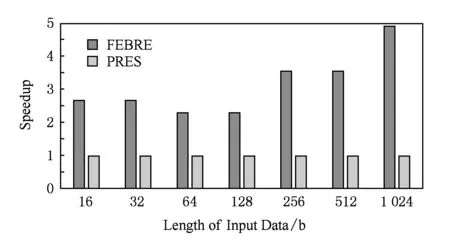
Fig. 6 Normalized comparing result of the coded vector set generation speed图6 编码向量集合生成速度的归一化对比

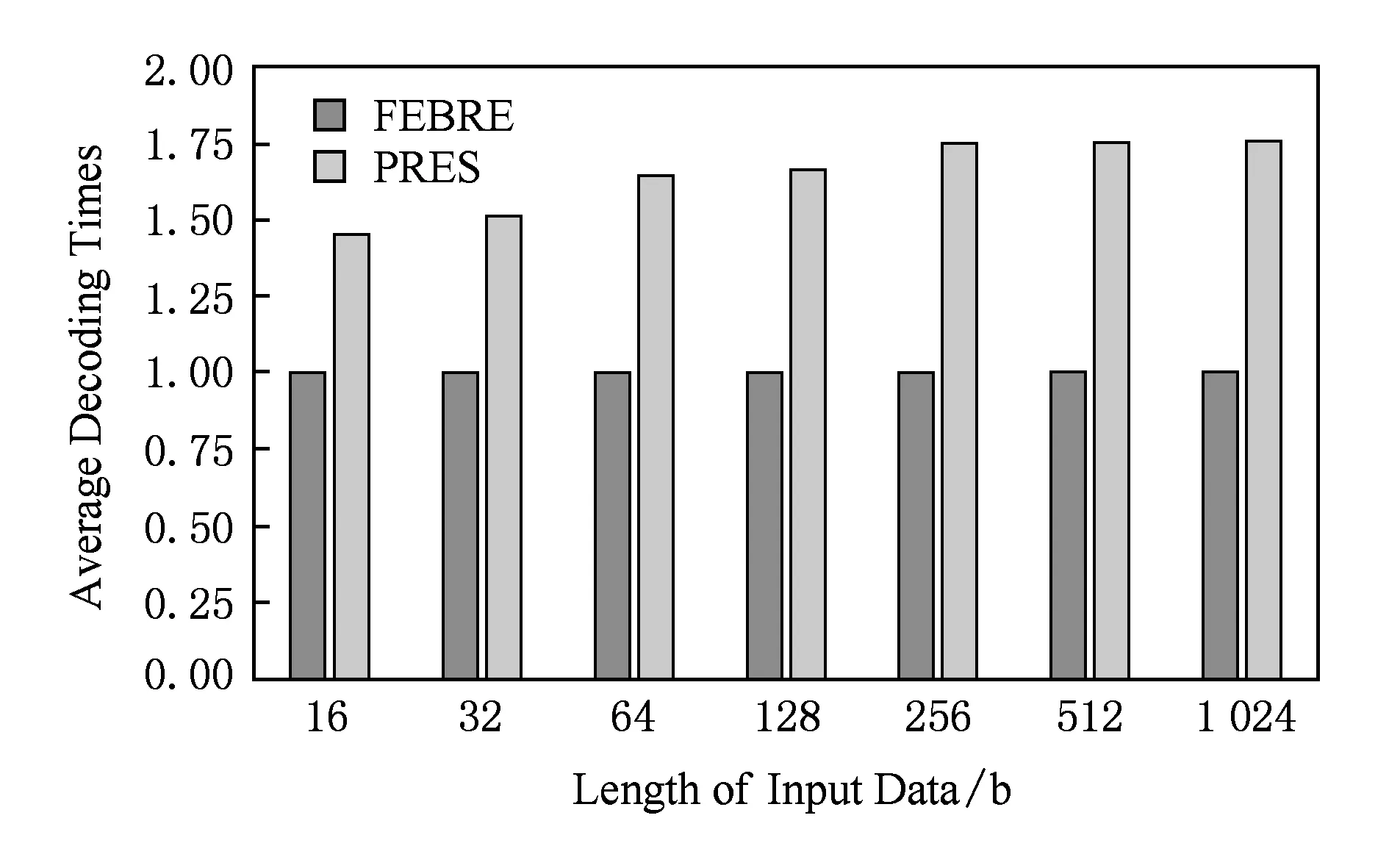
Fig. 7 The comparing result of the average decoding times in each reading operation图7 每次读取时所需的平均解码操作次数对比

4.5 解码速度对比

通过模拟多次读取，可以获得每次读取时2种方法的平均解码次数.如图7所示，每次读取时，FEBRE方法比PRES方法少用0.45次解码操作.

究其原因，FEBRE中的每个编码向量仅需要一次解码；而在PRES中，编码向量的解码次数依赖于该向量被生成时所用到的编码次数，而且二次编码向量远多于一次编码向量的数量.因此，在解码算法相同的前提下，每次读取时所需的解码操作次数是决定2种方法读取速度的最主要因素.

4.6 位翻转减少能力对比

图8中给出了FEBRE方法与PRES，Flip-Min，Flip-N-Write(FNW)方法在写入量减少能力上的归一化对比结果.此处的写入量采用每次写入时的平均翻转位数来计量.相比于PRES方法，FEBRE方法在每次写入中，平均减少了5.13%的位翻转数量；而相比于其他方法，FEBRE方法的优势更加明显.鉴于FEBRE和所有参与测试的方法所用到的编码向量数量是一样的，因此FEBRE方法在这方面的优势相对于PRES,可以认为是来源于其编码向量集合中消除了重复元素；而相对于其他方法，则是来源于其产生的编码向量的分布更加随机.

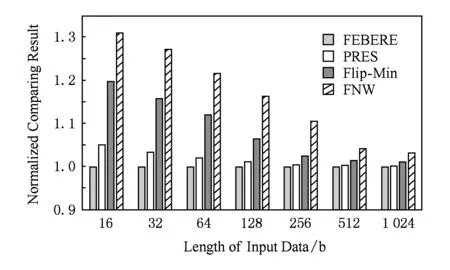
Fig. 8 Normalized comparing result of the average number of flipped bits per write图8 写入时平均翻转位数的归一化对比

4.7 FEBRE方法的可扩展性

对于FEBRE，PRES和Flip-Min等差分式方法而言，更多的编码向量虽然会带来更好的写入量减少效果，但也将以更高的空间占用作为代价.例如，即使编码向量为32个，待写入的数据长度为16 b时，任何上述方法的编码向量集合也将占用512 b的存储空间.此时，尽管这些方法仍然有效，但此时的空间占用将对存储系统产生巨大的负担，因此难以实用.本文仅讨论了16个编码向量的情况，并将对其他情况的讨论留做未来工作之一.

5 结 论

针对相变内存写入寿命有限的缺点，经典方法PRES方法可以很好地减少单次写入中改变的位数，从而减少总体写入量.然而，该方法的编码向量集合中存在大量的重复元素，而这一缺点会直接影响其写入减少效果和读写速度.本文首先指出了这一未被注意到的问题.之后，通过引入星型生成规则和广义编码方向模式的概念，本文提出的FEBRE方法解决了编码向量集合中的重复元素问题.此外，本文还设计了一种流水化的伪随机编码算法，不仅继承了原始算法的随机化能力，而且进一步加速了写入时所需的编码操作.综合以上这些因素，FEBRE方法不仅成功地提高了读写速度，而且进一步减少了每次写入时的平均写入量，因而成为了一种对比目前领先的PRES方法更加先进的差分式写入减少方法.

[1]Lee B C, Zhou P, Yang J, et al. Phase-change technology and the future of main memory[J]. Micro IEEE, 2010, 30(1): 143-143

[2]Lee B C, Ipek E, Mutlu O, et al. Architecting phase change memory as a scalable dram alternative[J]. ACM SIGARCH Computer Architecture News, 2009, 37(3): 2-13

[3]Qureshi M K, Srinivasan V, Rivers J A. Scalable high performance main memory system using phase change memory technology[C] //Proc of the 36th Annual Int Symp on Computer Architecture. New York: ACM, 2009: 24-33

[4]Qureshi M K, Karidis J, Franceschini M, et al. Enhancing lifetime and security of PCM-based main memory with start-gap wear leveling[C] //Proc of the 42nd Annual IEEE/ACM Int Symp on Microarchitecture. New York: ACM, 2009: 14-23

[5]Yang B D, Lee J E, Kim J S, et al. A low power phase-change random access memory using a data-comparison write scheme[C] //Proc of IEEE Int Symp on Circuits and Systems. Piscataway, NJ: IEEE, 2007: 3014-3017

[6]Cho S, Lee H. Flip-N-Write: A simple deterministic technique to improve PRAM write performance, energy and endurance[C] //Proc of the 42nd Annual IEEE/ACM Int Symp on Microarchitecture. New York: ACM, 2009: 347-357

[7]Luo Xiaolu, Liu Duo, Zhong Kan, et al. Enhancing lifetime of NVM-based main memory with bit shifting and flipping[C] //Proc of Int Conf on Embedded and Real-Time Computing Systems and Applications. Piscataway, NJ: IEEE, 2014: 1-7. DOI: 10.1109/RTCSA.2014.6910554

[8]Jacobvitz A N, Calderbank R, Sorin D J. Coset coding to extend the lifetime of memory[C] //Proc of Int Symp on High Performance Computer Architecture. Piscataway, NJ: IEEE, 2013: 222-233

[9]Seyedzadeh S M, Maddah R, Jones A, et al. PRES: Pseudo-random encoding scheme to increase the bit flip reduction in the memory[C] //Proc of Design Automation Conf. New York: ACM, 2015: 1-6. DOI: 10.1145/2744769.2755440

[10]Seyedzadeh S M, Maddah R, Kline D, et al. Improving bit flip reduction for biased and random data[J]. IEEE Trans on Computers, 2016, 65(11): 3345-3356

Gao Peng, born in 1982. PhD candidate. His main research interests include computer architecture, non-volatile memory.

Wang Dongsheng, born in 1966. PhD, professor, PhD supervisor. His main research interests include computer architecture, distributed system, and non-volatile memory.

Wang Haixia, born in 1977. PhD, associate professor. Her main research interests include computer architecture, network on chip, and memory hierarchy.

Increasing PCM Lifetime by Using Pipelined Pseudo-Random Encoding Algorithm

Gao Peng1,2, Wang Dongsheng2, Wang Haixia2

1(DepartmentofComputerScienceandTechnology,TsinghuaUniversity,Beijing100084)2(ResearchInstituteofInformationTechnology,TsinghuaUniversity,Beijing100084)

Phase change memory (PCM) is a promising technique due to its low static power, non-volatility, and density potential. However, the low endurance remains as the key problem to be solved before it can be widely used in practice. Generally, minimizing modified bits in write operation by writing the different bits, is an effective method to extend the lifetime of PCM. But it’s still challenging to reach the minimum without causing significant slowdown of read/write operations. To this end, we propose FEBRE: A fast and efficient bit-flipping reduction technique to extend PCM lifetime. The key idea of our method is to design and use a novel one-to-many parallel mapping before differential write stage. Specifically, FEBRE employs a new data encoding method to generate multiple highly random distributed encoded vectors from one writing data item, which thus increases the possibility of identifying the nearest one to stored data in those vectors. The other contribution of our technique is a pipelined pseudo-random encoding algorithm (PPREA). The new algorithm reduces writing overhead because it is able to accelerate the procedure of the one-to-many mapping. The experiment shows that our technique, compared with PRES, can reduce bit flips by 5.31% on average, and improve the encoding/decoding speed by 2.29x and 45%, respectively.

phase change memory (PCM); differential write; pseudo-random encoding algorithm; coding direction pattern; star-like generation rule

2017-02-14；

2017-04-21

国家重点研发计划(2016YFB1000303)；国家自然科学基金项目(61373025) This work was supported by the National Key Research and Development Plan of China (2016YFB1000303) and the National Natural Science Foundation of China (61373025).

汪东升(wds@tsinghua.edu.cn)

TP333