荷载横向扩散式组砌道面力学理论模型分析

刘 军 生

(中国民航大学机场学院，天津 300300)



荷载横向扩散式组砌道面力学理论模型分析

刘 军 生

(中国民航大学机场学院，天津 300300)

为了改善现有联锁块道面的荷载横向扩散能力并提高道面的承载能力，设计开发了具有较大尺寸的荷载横向扩散式组砌道面，并分析了组砌道面受荷时边界条件变化过程，提出了道面两阶段边界条件计算理论，并依据这两阶段边界条件建立了组砌道面的挠曲微分方程表达式。

组砌道面，力学理论模型，荷载扩散效应，边界条件

组砌路面是一种采用不同形状和尺寸的砖块、石块或预制混凝土块铺筑的路面，使用中可以满足不停航要求下的快速施工以及快速更换与修复等要求。目前可在很多城市道路、人行道、广场、公园以及一些景区等轻载道路中见到其广泛应用，但由于其承载能力无法满足较重荷载下的使用要求，使其在港口、码头、机场等工程中的应用十分匮乏[1]。为此，本文设计了具有较大尺寸的荷载横向扩散式组砌道面，研究了该组砌道面的力学理论模型。

1 砌块设计

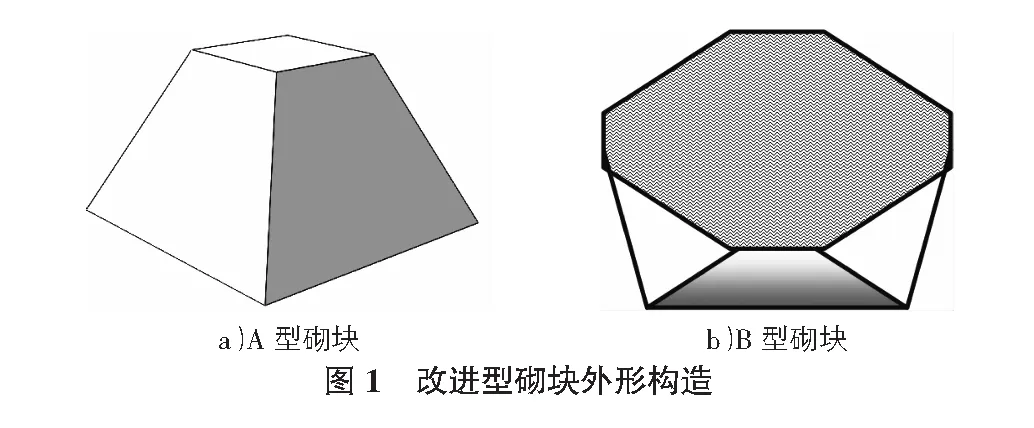
为增强组砌道面结构中块体之间的横向传荷能力，提高其承载能力，其实现途径之一就是基于相邻块体之间的衔接构造产生竖向力向水平力转变。从固体力学的基本原理来看，当力通过斜

界面传递时，其正压力会分解为垂直分力和水平分力，这种被分解的力就会施加到相邻块体之上。基于上述原理，可将块体单元设计为两类不同尺寸和形状的块体，并且将其分别定义为A块体和B块体，其基本形状如图1所示。利用A,B两类块体的组合铺砌可形成对竖向荷载有效转移的道面结构，如图2所示。

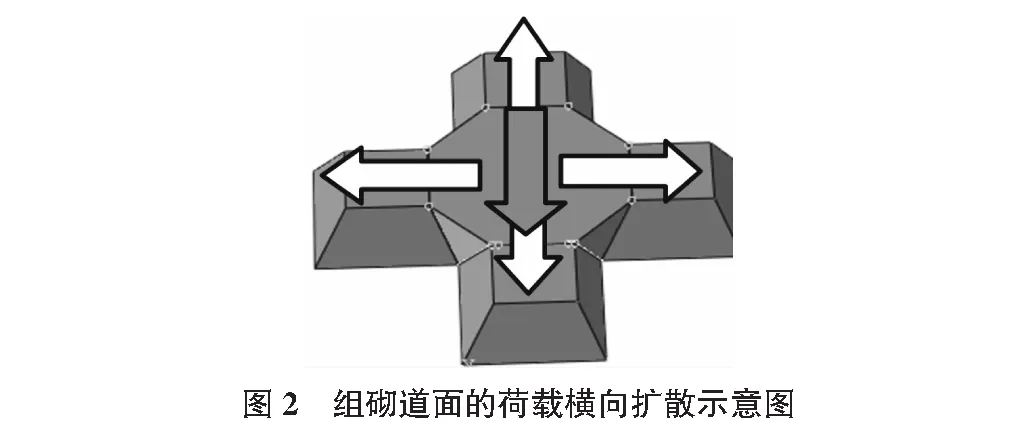
当某一竖向集中荷载作用在B块体上时，其承接该竖向力的B块体则可通过四个斜侧面将相当部分荷载施加到相邻A块体斜面上，从而降低了B块体底面对基层结构的压强。当某一竖向集中荷载作用在A块体上时，由于A块体本身的底表面积显著大于其顶面积，使得块体底面对基层结构的压强也显著降低。可见，无论集中荷载施加在哪一类块体上，其竖向荷载传递到基层顶面后都会由更大的面积所承受，从而可显著降低对基层结构的负荷作用。

2 组砌道面边界条件分析

组砌道面结构由于荷载的作用嵌挤程度会有一个逐渐加强的过程，这个过程的存在决定了组砌道面结构的工作状态在各个阶段不甚相同。因此，当选择道面结构若干块体单元为研究对象时，其边界条件也是存在一个变化过程的，并不是仅仅为简单的四边自由，四边简支或者四边固定。在组砌道面结构加载过程中，块体间的嵌挤程度会有一个加强过程，在加载初期，由于施加的荷载较小，块体间接触较为自由，嵌挤程度较为松弛，在很小变形的一个短暂范围内，块体单元四周的边界条件可以看作为四边自由的道面结构，此时，在荷载的继续作用下，块体单元可以发生相对较小的位移，对于相邻块体来说，块体间组合形成的约束几乎没有。这一加载初期可以看作为组砌道面结构块体单元边界条件的第一阶段，也就是边界条件为自由边界阶段[2]。

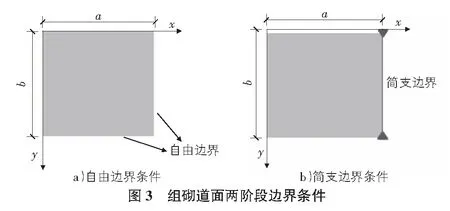
随着荷载的继续增加，块体单元在发生一定位移后，块体的移动趋势将受到限制，块体之间将会产生一定的应力作用，进而使得块体之间的接触更加紧密。此时，在荷载的作用下，块体单元四周的应力和变形将会受到周围相邻块体的约束作用，这个时候的约束状态不可以再看作是自由边，而可以看作为四边简支的约束状态。在这一期间，由于块体单元约束状态的改变，块体间力的作用发生改变，道面结构状态也已发生变化，这个阶段可以看作为组砌道面结构块体单元边界条件的第二阶段，也即边界条件为简支约束阶段。在经过面层等效后，其边界条件可以看作为一矩形薄板的边界条件，见图3。

3 力学理论模型简化分析与建立

3.1 组砌道面面层等效

在进行组砌道面结构的力学行为分析时，可将一定范围内的组砌道面面层等效为一柔性板，等效后的面层结构特性用当量模量E和泊松比μ表示，据此构建其力学模型。

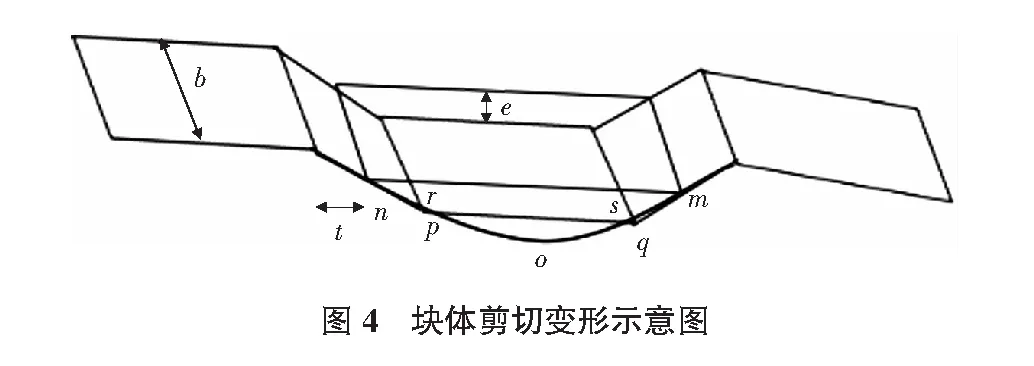
由于组砌道面结构在外部荷载作用下的变形主要为剪切变形，因此可用剪切能等效原理来近似求得等效板的当量模量[3]，假设外力在假定的挠曲面上所作的功与外部荷载在真实变形状态下所作的功相等，剪切变形示意图如图4所示，h为砌块厚度，

a=b为砌块宽度，t为砌块水平错开距离的1/2，与块体侧面倾角有关，e为相邻砌块竖直变形的1/2。

通过上述等效原理可以近似求得道面面层当量模量为：

(1)

其中，a为块体平面尺寸；t为砌块水平错开距离的一半；Gs为砂的剪切模量；μ为泊松比。

上述面层等效在一定程度上可以反映面层块体的特性，且由当量模量的计算公式可以看出，当量模量与块体的尺寸，砌块侧面倾角等参数有关。

3.2 力学模型建立

第一边界条件阶段为组砌道面结构边界条件是四边自由边阶段[4,5]。对于弹性地基上的矩形薄板，当四边为自由边界时，那么其四个板边边缘既没有弯矩和扭矩，也没有垂直剪力。因此其边界条件的控制方程为：

在x=0，x=a的自由边界上，有：

(2)

将板边扭矩等效成剪力后，则有：

(3)

根据薄板的基本方程，用挠度表示则有：

(4)

同理，在y=0，y=b的自由边界上，边界条件有：

(5)

上述将板边扭矩等效为剪力后，在板边两端还有两个集中力，其大小应该和板边相应的两个板角扭矩大小相等。也即在板角(0，0)，(0，b)，(a，0)，(a，b)处，边界条件为：

(6)

为了得到弹性半空间地基上的薄板弯曲解析解，可将挠度表示为带有补充余项的双重余弦级数：

(7)

其中，βnm，Dn,Fn,Gm,Hm均为待定系数，式(7)可以满足边界条件式(4)～式(6)。

此外，将上部作用荷载以及地基反力也写成双重余弦级数：

(8)

其中，

(9)

(10)

(11)

将上述式子与薄板基本方程对比，并利用傅里叶变换，代入边界条件，就可以求得待定系数，进而求得四边自由板的弯曲解析解，具体变换过程及其解法可采用西安建筑科技大学王春玲提出的方法进行求解[6]。

第二边界条件阶段为组砌道面结构边界条件是四边简支边阶段[7]。此时组砌道面的受力较为复杂，可以看作板边约束条件为一集中力作用在板的中点，在四条边界上有均布压力F的作用下，并在四边简支条件下的微分方程的弯曲求解。

当薄板四边为简支边，且支座无沉陷时，其边界条件可表示为：

(12)

(13)

运用那维埃解法将挠度表达式取为下列形式[8,9]：

(14)

其中，Anm为待定系数，n和m为任意正整数。将式(14)代入薄板微分方程可得：

q(x,y)-p(x,y)

(15)

将荷载以及地基反力同样展开为相同形式的双重三角级数，有：

(16)

(17)

对于式(16),式(17)进行两边同乘以正弦级数并进行相关转换，可以求得系数Bnm,Cnm,如下：

(18)

(19)

将Bnm,Cnm代入式(16),式(17)可得：

(20)

将式(20)代入式(15)，可以求得系数Anm，如下：

(21)

当薄板任意位置(x0，y0)作用一集中荷载q0时，荷载q只在该位置(x0，y0)处的微分面积上等于q0/dxdy，而在其余各处等于零。所以式(21)可以表示为：

(22)

将式(22)代入式(14)得到：

(23)

式(23)中D为板的弯曲刚度，它与板体弹性模量和泊松比有关，根据组砌道面的等效当量模量，可以知道其表达式为：

(24)

式(23)即为薄板挠度解得表达式，当知道地基反力p(x,y)时，便可以算得组砌道面等效板挠度，进而算得各内力。

4 结语

为改善组砌道面的荷载扩散效应，提高其承载能力，本文设计开发了荷载横向扩散式组砌道面。通过对其面层进行等效处理，对其受荷过程中边界条件分析，提出了两阶段边界条件处理方法，并结合弹性半空间地基上的小挠度薄板理论，对不同边界条件下的道面弯曲进行了相关求解分析，得到了道面在不同受荷阶段的挠曲方程，为该组砌道面在相关重载工程中的应用奠定了一定的理论基础。

[1] 吴靖宇.浅谈联锁块路面的应用[J].市政技术,2002(2)：26.

[2] 张 恒.型钢—预应力混凝土快速组合道面结构性能研究[D].天津:中国民航大学硕士学位论文,2016.

[3] 李宇峙,邵腊庚.嵌挤式混凝土块路面结构的模型理论[J].中国公路学报,1998(1)：76.

[4] 阎红梅,崔维成,刘应中.弹性地基上四边自由矩形板问题的一种新型挠度函数[J].船舶力学,2003(2):61-70.

[5] 钟 阳,张永山.弹性地基上四边自由矩形薄板的解析解[J].应用数学和力学,2006(6):735-740.

[6] 王春玲,黄 义.弹性半空间地基上四边自由矩形板的弯曲解析解[J].岩土工程学报,2005(12):1402-1407.

[7] 程选生,杜永峰.横向变温下四边简支矩形薄板的解析解[J].低温建筑技术,2006(4):76-78.

[8] 王志伟.Pasternak地基上四边简支矩形薄板的弯曲问题[J].洛阳大学学报,2004(4):74-77.

[9] 祝文畏,杨学林,岳燕玲.考虑扭矩影响的四边简支矩形板内力分析及配筋修正[J].工程力学,2012(9):259-264.

On dynamic theory model of masonry pavement with horizontal diffusion loading

Liu Junsheng

(CollegeofAirport,CivilAviationUniversityofChina,Tianjin300300,China)

In order to improve the loading horizontal diffusion capacity of the existing locking pavement and promote the loading capacity of the pavement, the paper designs and develops the larger masonry pavement with loading horizontal diffusion, analyzes the changes of the boundary conditions with the masonry loading pavement, points out the calculation theory for the two-phase boundary conditions of the pavement, and establishes the deflection differential equation of the pavement.

masonry pavement, dynamic theory model, loading diffusion effect, boundary condition

1009-6825(2017)14-0131-03

2017-03-08

刘军生(1991- )，男，在读硕士

V351.11

A