金属疲劳损伤的研究现状★

肖 敏 杨 杰 李玉果

(中南林业科技大学土木工程与力学学院,湖南 长沙 410004)



金属疲劳损伤的研究现状★

肖 敏 杨 杰 李玉果

(中南林业科技大学土木工程与力学学院,湖南 长沙 410004)

介绍了金属疲劳损伤的研究历程，概述了金属疲劳中几种典型的本构方程的特点及其应用现状，并分析了影响本构方程的因素，指出如何修正受诸多影响下的本构方程，是研究金属疲劳损伤的难点之一。

金属疲劳，本构方程，应变速率，温度

0 引言

相较于其他材料，金属常给人一种坚硬无比的感觉。但实际上，在各种外力的反复作用下，金属也会产生疲劳，且一旦疲劳便会因不能及时恢复而造成十分严重的后果。自第二次世界大战以来，因金属疲劳失效而造成的工程事故，已是数不胜数。据统计，现代工业中零件的损坏，有近80%都是由于金属疲劳所引起的[1]。其原因是金属内部结构并不均匀，在应力的集中作用下，往往会产生裂纹。裂纹继续扩展后，进一步降低了材料性能，从而导致了工程失效问题。由于金属材料在国防和民用工业中的广泛应用，对其结构的安全和可靠性的研究已引起国内外力学工作者的普遍重视[2,3]。为此金属材料的疲劳损伤方面的研究，已逐渐成为力学领域中研究的热点，在化工、轻纺、建筑、机械等行业以及日用品工业中，愈来愈显示出广阔的应用前景。

1 金属疲劳损伤发展简史

国外很早就开始了金属疲劳损伤方面的研究，有记载的最早进行疲劳试验的是德国的W.A.艾伯特，1829年他对用铁制作的矿山升降机链条进行了反复加载实验[4]。但真正将疲劳同金属失效联系起来的却是法国的J.-V.彭赛列，他在著作中首先论述了疲劳问题并提出了“疲劳”这个名词[5]。疲劳研究的奠基人则是德国的A.沃勒，他在19世纪50年代～60年代最早得到表征疲劳性能的应力—寿命曲线[6]。1884年包辛格在进行疲劳试验的验证时，提出了应力—应变滞后回线的概念，但未得到相应的重视。直到1952年，邱杨在做铜棒实验时引用了包辛格的观点，并将之命名为包辛格效应，包辛格才因此成为第一个研究循环应力与应变关系的人[7]。

20世纪初，随着宏观—细观的力学理论及其实验方法的发展，人们开始使用金相显微镜来研究疲劳机制。通过观测金属内部组织结构的变化，这一时期也涌现了大量的研究成果。1903年，欧文和汉弗莱的研究从结晶组织层面，指出疲劳变形也与单调变形相关，皆由滑移所产生[8]。在他的发现上，许多学者进行了后续工作，并将之拓展到了疲劳研究上。1920年格里菲斯发表了他用玻璃研究脆断的理论计算和实验结果，从中他得出了两者间的关系式，因而被称为“断裂力学之父”[9]。

而关于疲劳理论方面的研究，可追溯到19世纪20年代，英国的高夫在1924年出版了第一本系统研究疲劳的专著——《金属疲劳》[10]。1937年，为了研究缺口的疲劳效应，德国的诺伯提出了“体素”和应力梯度的概念[11]。1945年，美国人迈因纳从以往的疲劳累积损伤研究出发[12]，结合帕尔姆格伦1924年提出的线性累积损伤理论[13]，提出了帕尔姆格伦—迈因纳线性累积损伤法则，此法沿用至今。尽管该理论存在许多缺点，却仍是进行疲劳预测的重要方法之一[14-16]。

综上所述，从人们认识和开始研究疲劳问题，已有150多年的历史。而研究疲劳的最终目的，是为了延长结构或构件的使用寿命，优化其材料性能。要计算疲劳寿命，需有一个损伤演化方程作为理论依据。结合相关的疲劳损伤理论，并将影响疲劳寿命的主要因素考虑进来，这便是疲劳损伤本构方程的由来。

2 金属疲劳损伤本构方程

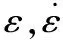
早在20世纪初，人们就对金属材料加工过程中普通存在的硬化现象进行了大量研究，并从流变学的视角出发，建立了金属材料模型[17]。

σ=kεn

(1)

其中，σ为应力；ε为应变；k为强度因子；n为加工硬化指数。

对模型建立应力—应变曲线，并采用双对数坐标时，图像呈现为直线。这是由于n为常数，适合描述lnσ与lnε呈线性关系的加工硬化曲线。但在实际工程中，材料的加工硬化曲线即使在双对数坐标中，并不完全为直线[18,19]。周维贤[20]分析了现有的加工硬化曲线的数学模型，考虑到弹性极限的影响，对半经验模型进行的修正如下：

σ=σ0+kεn

(2)

此方程适用于描述双对数坐标中明显上挠的加工硬化曲线，其中σ0为弹性极限。在双对数坐标中，材料的加工硬化曲线有上下挠之分，且各有一定的适应范围。在此基础上，他还提出了新的数学模型。

σ=BεN/(1+D1ε+D2ε2)

(3)

其中,D1,D2均为常数，当它们取不同的值时，硬化指数n也随D1，D2的变化趋势而改变。

上述模型只适用于部分金属材料的加工硬化状态，而低层面心立方金属，常用Ludwigson[21]于1974提出的数学模型。

σ=k1εn1+e(k2+n2ε)

(4)

其中,k1为强度系数;n1为硬化指数；k2,n2的值为常数，用来修正模型；ek2用来表达材料的屈服应力。

后来，Tian[22]研究了稳定的奥氏体钢316L,Fe-25Cr-22Ni,Fe-21Cr-9Mn-9Ni及Fe-23Mn-4AI-5Cr-0.3C的流变行为，并修正了加工硬化模型。

σ=Kεn1+n2lnδ

(5)

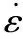
除却经验模型之外，研究学者们还从疲劳损伤的理论出发，推导出了具有实际物理意义的理论模型。若将高温变形看成一个热激活效应，则包含变形激活能Q和温度T的本构方程为：

(6)

其中，A1为材料参数；g(σ)为含有应力的函数；Q为变形的激活能；R为气体常数；T为热力学温度。

这便是Arrhenius方程的表达式，有指数方程、幂指数方程和双曲正弦方程三种。不同种类有不同的应用范围。其中指数形式适用于流变应力较高的材料，幂指数形式适用于流变应力较低的材料，而双曲正弦形式则考虑了不同应变、应变速率和温度对于材料性质的影响。此模型形式简单，参数获取相对容易，且容易应用到数值模拟中。但传统的Arrhenius方程并未考虑应变的影响，从而影响了数值模拟的精度。为了提高精度，Lin在预测42CrMo钢的高温流动应力时，引入应变因子，对Arrhenius本构模型中的应变速率进行了指数修正[23]。之后，该方法被用于含Ti奥氏体不锈钢川[24]和Ti6246[25]等金属的流动应力预测。

修正后的Arrhenius本构模型虽然结合考虑了应变、应变速率的影响，但其主要建立在高温变形的基础上，这就使得Arrhenius方程的应用受到了一定的限制。

3 结语

总结以上所分析的研究成果可以发现：对于金属疲劳损伤的研究目前正在开展，研究相关内容还不够完善。关于金属疲劳损伤的本构方程大多形式复杂，需要的参数较多，不便于实际运用。同时，一些本构方程仅考虑了单一因素的影响，造成模拟的精度不够高。因此，从发展来看，在原有的理论基础上，该如何修正受诸多因素影响下的本构方程，仍是研究金属疲劳损伤的难点之一。

[1] 倪 姳.“金属疲劳”与“免疫疗法”[J].吉林劳动保护,2014(3):41.

[2] Liakat M,Khonsari M M.An experimental approach to estimate damage and remaining life of metals under uniaxial fatigue loading[J].Materials & Design,2014,57(5):289-297.

[3] Ma S,Yuan H.A continuum damage model for multi-axial low cycle fatigue of porous sintered metals based on the critical plane concept[J].Mechanics of Materials,2017(104):13-25.

[4] 徐 濒.疲劳强度[M].北京：高等教育出版社,1988:22-26.

[5] 闻步正.装载机驱动桥主减速器疲劳可靠性的研究[D].杭州：浙江理工大学,2011.

[6] 曾春华,邹十践.疲劳分析方法及应用[M].北京：国防工业出版社,1991:28-35.

[7] 孙 猛.包辛格效应测试机的优化设计及实验分析[D].沈阳:沈阳工业大学,2015.

[8] 刘 翾.479Q型发动机曲柄连杆机构的疲劳寿命分析[D].天津：河北工业大学,2009.

[9] 付亚冰.航空发动机和传动系统中电阻应变测试技术应用研究[D].长沙：湖南大学,2013.

[10] 雷庆兰.中小跨径钢筋混凝土拱桥在车辆荷载作用下的疲劳特性研究[D].重庆：重庆交通大学,2013.

[11] 刘俭辉.拉压载荷下304不锈钢低周疲劳断裂特性的研究[D].兰州：兰州理工大学,2011.

[13] Cai F,Wang X,Liu J,et al.Fatigue Life Analysis of Crane K-Type Welded Joints Based on Non-Linear Cumulative Damage Theory[J].Strojniski Vestnik,2014,60(2):135-144.

[14] Mohammadzadeh S.Stress-based fatigue reliability analysis of the rail fastening spring clipunder traffic loads[J].Latin American Journal of Solids & Structures,2014,11(6):993-1011.

[15] Zhao X.The application of strain field intensity method in the steel bridge fatigue life evaluation[J].Proceedings of SPIE-The International Society for Optical Engineering,2012(13):61.

[16] Lappi J.Utilization potential of high strength steel in fatigue loaded floating production storage and offloading unit structures[J].Soc.bot.fr,2015,125(1-2):175-181.

[17] 王小巩.抗大变形管线钢热变形行为及流变应力模型研究[D].秦皇岛：燕山大学,2013.

[18] 陈克信.GH3535塑性加工残余应力研究[D].上海：东华大学,2015.

[19] Pluta Z,Hryniewicz T.Novel Modeling of the Work-Hardening Curve[J].International Letters of Chemistry Physics & Astronomy,2013(9):73-90.

[20] 周维贤.描述钢板硬化曲线的一个新数模[J].材料研究学报,1989,3(4):325-330.

[21] Ludwigson D C.Modified stress-strain relation for FCC metals and alloys[J].Metallurgical and Materials Transactions B,1971,2(10):2825-2828.

[22] Tian X,Zhang Y.Mathematical description for flow curves of some stable austenitic steels[J].Materials Science & Engineering A,1994,174(1):11-13.

[23] Pu Z J,Wu K H,Shi J,et al.Development of constitutive relationships for the hot deformation of boron microalloying TiAl Cr V alloys[J].Materials Science & Engineering A,1995,192(94):780-787.

[24] 甘春雷,郑开宏,戚文军,等.考虑应变补缩的6063铝合金高温流变应力本构方程[J].中国有色金属学报(英文版),2014(11):3486-3491.

[25] Nourollahi G A,Farahani M,Babakhani A,et al.Compressive deformation behavior modeling of AZ31 magnesium alloy at elevated temperature considering the strain effect[J].Journal of Materials Research,2013,16(6):1309-1314.

Research status of metal fatigue damage★

Xiao Min Yang Jie Li Yuguo

(InstituteofRheologicalMechanicsandMaterialsEngineering,CentralSouthUniversityofForestryandTechnology,Changsha410004,China)

The research status of metal fatigue damage is introduced, the characteristics and applications of several typical constitutive equations of metal fatigue are summarized, and the factors which influence the constitutive equation are discussed. It illustrates how to modify constitutive equation with various influences is one of difficulties for studying the mental fatigue damage.

metal fatigue, constitutive equations， strain rate, temperature

1009-6825(2017)14-0106-03

2017-03-01

肖 敏(1985- )，女，在读硕士

TU511

A

★:2016湖南省教育厅重点项目(16A220);大学生研究性学习和创新性实验计划项目(湘教[2015]269号)