多项式模型在导航卫星钟差预报中的应用研究
2017-06-22朱陵凤韩春好陈刘成
朱陵凤,李 超,韩春好,刘 利,陈刘成
(北京卫星导航中心,北京 100094)
多项式模型在导航卫星钟差预报中的应用研究
朱陵凤,李 超,韩春好,刘 利,陈刘成
(北京卫星导航中心,北京 100094)
为了解决导航卫星钟差预报精度随时间不断衰减问题,提出了基于多项式的卫星钟差预报模型优化方法。该方法通过优化预报采用的数据资料长度和多项式模型阶次,实现了高精度的卫星钟差短/中/长期预报。为验证该方法的可行性和有效性,利用实测的COMPASS导航卫星钟差数据进行钟差预报精度分析。结果表明,当多项式模型满足资料长度和模型阶次的最佳配置时,可有效解决导航卫星钟差预报精度随时间不断衰减的问题。
北斗卫星导航系统;卫星钟差预报;多项式模型;模型阶次;资料长度
0 引言
区域导航系统地面段部分采用区域监测网,非地球同步轨道的导航卫星一旦运行到所有区域监测网点都监测不到的弧段内,其星载原子钟与系统时间之间的同步只能由卫星钟自己维持,因此,必须对该导航卫星钟差进行预报[1]。
近年来,部分学者将灰色系统、Kalman滤波器、ARIMA模型、神经网络、泛函网络、小波变换和线性组合模型等用于导航卫星钟差预报,取得了一些进展。灰色系统只需少量的原始数据就可通过生成变换来建立灰色模型,大大提高了建模速度和计算速度[2]。然而,模型预报精度受少量数据质量的影响很大。文献[3]讨论了原始数据序列的预处理和模型优化方法,给出了一种通过参数优化模型的方法,一定程度上提高了灰色模型用于卫星钟差预报的精度。GPS运用Kalman滤波模型推求原子钟的运行参数,文献[4]为了保证Kalman滤波模型的性能,利用小波分析对观测序列进行降噪,剔除粗差的同时,减弱了函数模型和随机模型误差对滤波参数的影响,有效提高了Kalman滤波求解精度。文献[5-6]在对原始钟差数据进行二次差分使之成为平稳的时间序列后,建立了卫星钟差的ARIMA预报模型,得到了理想的卫星钟差预报结果。文献[7-8]考虑到RBF神经网络具有曲线拟合平滑度好、学习训练速度快、收敛速度快和残差波动小的优点,将RBF神经网络用于卫星钟差短期预报,取得了良好的预报效果。文献[9-10]利用多项式模型进行原子钟趋势项的提取,再利用泛函网络实现剩余残差部分的周期性和随机性预测,提高导航卫星钟差预报精度。文献[11]通过小波变换把钟差时间序列分解成具有不同频率特征的分量,然后根据各分量的特点构建不同的最小二乘支持向量机模型进行预报,最后将各分量的预报结果进行叠加得到最终的钟差预报值,预报效果优于单一的最小二乘支持向量机模型。文献[12]对灰色模型与二次多项式模型进行了线性组合,在保证预报结果可靠性的基础上,提高了结果的稳定性和准确性。
鉴于星载原子钟物理特性[13]与多项式模型的吻合性,2阶多项式模型在卫星导航系统钟差预报中,仍然具有不可替代的优势作用,然而,随着预报时间的增长,2阶多项式模型累积预报误差不断增加,不能满足实际应用中的精度要求。
本文提出了基于多项式的卫星钟差预报模型优化方法,通过合理设置预报资料长度和多项式模型阶次,实现高精度的导航卫星钟差预报。实测数据表明,只要预报资料长度与模型阶次达到最佳的适应状态,导航卫星钟差短/中/长期预报精度均能实现大幅提高。
1 多项式通用模型

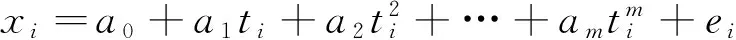
(1)
式中,a0,a1,…,am为拟合系数;m为多项式阶次;ei为模型误差。
式(1)可表示为矩阵形式[14]:
X=Ha+e。
(2)
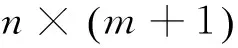
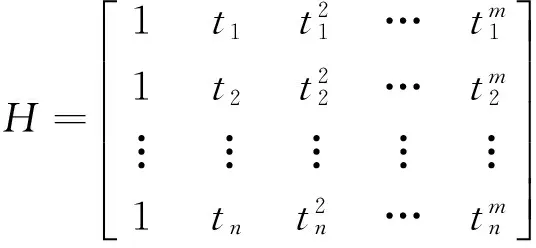
(3)
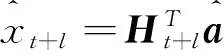
(4)

2 模型阶次的选取
原子钟的变化包括系统性变化和随机性变化两部分,系统变化部分可用一个确定性函数模型来描述,而随机变化部分是一个随机量,只能从统计意义上来分析。
理想条件下,原子钟系统性变化部分主要包括时间偏差、频率偏差和线性频漂3部分。当原子钟的线性频漂不明显时,一般用1阶多项式模型拟合时差和频差,并进行钟差预报;当原子钟受频率老化率影响较大时,存在明显的频率漂移,用1阶多项式模型拟合预报不能取得好的效果,此种情况下,若预报时间不是很长时,可以认为其频率漂移是一常量,用2阶多项式模型[16]估计时差、频差和线性漂移这3个参数,再进行钟差拟合预报,通常情况下预报精度不会太低;若预报时间较长时,频率漂移并不是常量,传统的2阶多项式模型不能高精度地实现钟差拟合预报[17]。
对于在轨运行的原子钟而言,不仅受到自身生命周期内频率老化的影响,而且受到复杂多变的太空环境的影响,二者的共同影响必然导致其随机性变化规律很难预测。若考虑更高阶次的多项式模型,与真值更好地逼近效果能够达到原子钟系统性变化和随机性变化兼顾的高精度拟合效果,但是,太高阶次的多项式模型在预报过程中会出现发散的“龙格”现象[18],导致预报精度衰减快。因此,本文选取了1阶、2阶、3阶、4阶和5阶共5种多项式模型阶次,进行卫星钟差拟合预报。
3 实测数据试验分析
采用COMPASS系统GEO-01卫星星载铷原子钟2016年1月8~13日、GEO-03卫星星载铷原子钟2016年2月10~15日、GEO-04卫星星载铷原子钟2016年3月24~29日共3组连续6天的实测卫星钟差数据进行多项式模型优化试验。采用72种不同资料长度(1/2/3/4/…/71/72h)模式下的5种不同阶次(1/2/3/4/5)多项式预报模型,取第4天0点为预报起始点,以1h为滑动窗口,分别进行1h、2h、12h、24h和72h的钟差预报,采用连续多组的均方根误差RMS(RootMeanSquareError)来衡量不同资料长度不同模型的预报精度,其公式为:
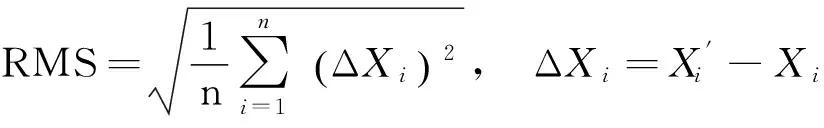
(5)


表1 导航卫星钟差最优预报模型与预报精度统计表
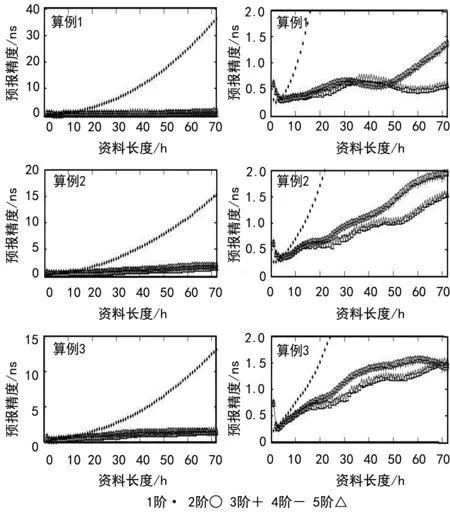
图1 卫星钟差1 h预报结果及局部放大

图2 卫星钟差2 h预报结果及局部放大
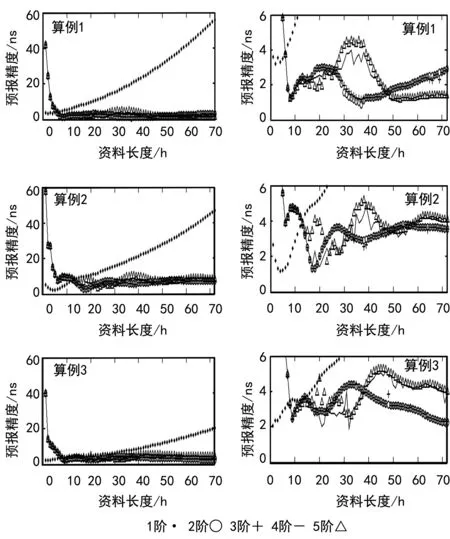
图3 卫星钟差12 h预报结果及局部放大

图4 卫星钟差24 h预报结果及局部放大
由图表可知:① 短期(1 h、2 h)预报选取1 h、2 h资料长度采用1阶多项式模型预报精度最高,1 h预报精度优于0.3 ns,2 h预报精度优于0.5 ns,但是随着资料长度的增长,1阶多项式模型预报精度衰减很快;若采用2阶、3阶、4阶和5阶多项式模型预报,预报精度随资料长度变化不大,72种不同资料长度的预报精度均可达2.5 ns。② 中长期(12 h、24 h和72 h)预报选取合适长度的资料采用2阶、3阶、4阶和5阶多项式模型预报精度可达最高,12 h预报精度优于2 ns,24 h预报精度优于2.5 ns,72 h预报精度优于3 ns;不同星载钟的最优模型差异较大,2阶和3阶多项式模型居多;③ 短中长期预报过程中,1阶多项式模型随资料长度的增加衰减很快,2阶和3阶多项式模型预报结果基本一致且稳定性高,4阶和5阶多项式模型预报结果基本一致,偶尔可达最优模型精度,但是稳定性稍差。

图5 卫星钟差72 h预报结果及局部放大
4 结束语
本文通过优化多项式模型阶次和资料长度,使二者达到最佳适应状态,实现了多项式模型预报导航卫星钟差的最高精度,成功解决了预报误差随预报时长迅速增大的问题。COMPASS导航卫星实测数据验证结果表明:1阶多项式模型适用于1 h、2 h的短期钟差预报,但是资料长度不宜太长;2阶和3阶多项式模型选取合适的资料长度可以满足高精度中长期预报;4阶和5阶多项式模型稳定性较差,不考虑用作钟差预报。因此,唯有合理配置预报资料长度和模型阶次,多项式模型在导航卫星钟差预报中才会呈现更好的应用价值。
[1] 吴海涛,李孝辉,卢晓春,等.卫星导航系统时间基础[M].北京:科学出版社,2011.
[2] 李玮,程鹏飞,秘金钟.灰色模型在快速卫星钟差预报中的应用[J].测绘科学,2010,35(3):43-45.
[3] 路晓峰,杨志强,贾小林,等.灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2008,33(5):492-495.
[4] 王继刚,胡永辉,何在民,等.基于小波降噪的Kalman滤波预报卫星钟差[J].测绘科学,2012,37(5):9-11.
[5] 徐君毅,曾安敏.ARIMA(0,2,q)模型在卫星钟差预报钟的应用[J].大地测量与地球动力学,2009,29(5):116-120.
[6] 范旭亮,王晓红,张显云,等.基于ARIMA模型的卫星钟差短期预报研究[J].测绘与空间地理信息,2015,38(1):104-106.
[7] 郭承军,滕云龙.神经网络在卫星钟差短期预报中的应用研究[J].测绘科学,2011,36(4):198-200.
[8] 张景元.基于神经网络的卫星钟差预报研究[J].计算机工程与设计,2014,35(9):3 254-3 257.
[9] 王颖,徐波,杨旭海.一种利用泛函网络进行导航卫星钟差预报的方法研究[J].宇航学报,2012,33(10):1 401-1 406.
[10] 季利鹏,徐波,高有涛.泛函网络在导航卫星钟差中长期预报中的应用[J].天文学报,2013,54(2):176-188.[11] 雷雨,赵丹宁,李变,等.基于小波变换和最小二乘支持向量机的卫星钟差预报[J].武汉大学学报(信息科学版),2014,39(7):815-819.
[12] 王继刚,胡永辉,何在民,等.基于修正线性组合模型的原子钟钟差预报[J].天文学报,2011,52(1):54-61.
[13] 郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州:解放军信息工程大学,2006.
[14] 隋立芬,宋力杰,误差理论与测量平差基础[M].北京:解放军出版社,2004.
[15] 黄维斌.近代平差理论及其应用[M].北京:解放军出版社,1992.
[16] 胡轩宇,黄勇,胡小工,等.单颗MEO卫星定轨中的二阶钟差模型[J].宇航学报,2009,30(3):924-929.
[17] 张杰,周渭,宣宗强,等.卫星钟差预报模型中周期项的选取方法及性能分析[J].天文学报,2013,54(3):282-290.
[18] 徐君毅,戴伟.一种新的长期卫星钟差预报方法[J].大地测量与地球动力学,2009,29(6):97-100.
Application of Polynomial Model in Satellite Clock Error Prediction
ZHU Ling-feng,LI Chao,HAN Chun-hao,LIU Li,CHEN Liu-cheng
(BeijingSatelliteNavigationCenter,Beijing100094,China)
In order to improve satellite clock error prediction precision,an optimum method based on polynomial model is proposed in this paper.By adjusting the amount of satellite clock data and the rank of polynomial model,different length predicting precision of satellite clock error are improved.To validate the feasibility and effectiveness of this method,this paper analyzes the predicting precision of satellite clock error through the statistics of COMPASS satellite clock error.The analysis shows the satellite clock error prediction precision can be improved,when the amount of satellite clock data and the rank of polynomial model are all optimized.
COMPASS;satellite clock error prediction;polynomial model;model rank;data length
10.3969/j.issn.1003-3106.2017.07.12
朱陵凤,李超,韩春好,等.多项式模型在导航卫星钟差预报中的应用研究[J].无线电工程,2017,47(7):51-54.[ZHU Lingfeng,LI Chao,HAN Chunhao,et al.Application of Polynomial Model in Satellite Clock Error Prediction[J].Radio Engineering,2017,47(7):51-54.]
2017-01-10
国家高技术研究发展计划(“863”计划)基金资助项目(2014AA123102)。
P228.9
A
1003-3106(2017)07-0051-04
朱陵凤 女,(1983—),硕士,工程师。主要研究方向:卫星导航与无线电时间比对技术。
李 超 男,(1981—),硕士,工程师。主要研究方向:卫星导航用户终端算法研究。
