旋转曲面及其方程

黄振华，祝秋文，胡清华

(1.湖北师范大学 数学与统计学院，湖北 黄石 435002；2.湖北师范大学 物理与电子科学学院，湖北 黄石 435002；3.黄石市第十四中学，湖北 黄石 435002)

旋转曲面及其方程

黄振华1，祝秋文2，胡清华3

(1.湖北师范大学 数学与统计学院，湖北 黄石 435002；2.湖北师范大学 物理与电子科学学院，湖北 黄石 435002；3.黄石市第十四中学，湖北 黄石 435002)

求旋转曲面的方程，是大一新生在学习过程中较为疑惑的。讨论了旋转曲面的旋转轴与母线的不同位置求解方程的基本思想与方法。

旋转曲面；旋转轴；母线；方程

《空间解析几何》是师范大学的一门专业基础课程，一般在新生入学第一学期就开设了此课程。为大学后续课程的学习起到基础作用，对学生今后从事的教育工作也具有指导性作用。因此，搞好解析几何课程的教学是适应高等教育培养具有创新精神和实践能力的高素质人才的需要。然而，在解析几何课程教学的过程中，部分学生对旋转曲面及其方程的学习觉得有一定的难度。本文将对旋转曲面方程的求解方法进行讨论，以降低新生学习之难度。

1 旋转曲面的概念

定义[1]在空间，一条曲线Γ绕着定直线l旋转一周所生成的曲面叫旋转曲面，曲线Γ叫旋转曲面的母线，定直线l叫旋转曲面的旋转轴。

母线Γ上任一点M1在旋转时形成一个圆，这个圆是通过点M1且垂直于旋转轴l的平面与旋转曲面的交线。称之为纬圆或纬线。

在通过旋转轴l的平面上，以l为界的每个半平面都与旋转曲面交成一条平面曲线，这些平面曲线叫做旋转曲面的经线。

经线绕着旋转轴l旋转一周与母线绕着旋转轴l旋转一周所形成的旋转曲面相同。所以，经线可以当做母线，而母线不一定是经线。

2 旋转曲面方程的求法

2.1 不论旋转轴与母线的位置关系时的求法

此情况下求旋转曲面的方程，是学生感觉到比较困难的。关键是对旋转曲面要有充分的理解，关于旋转曲面，当然可按照定义理解为母线绕旋转轴旋转而生成，还可理解为以旋转轴为连心线且垂直于旋转轴的平行圆叠加生成。求旋转曲面的方程，以后者理解思想居常见，具体求法有：

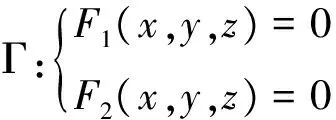
(1)

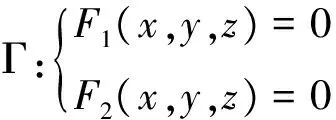
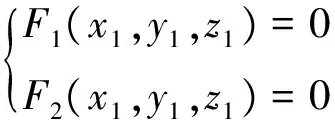
(2)

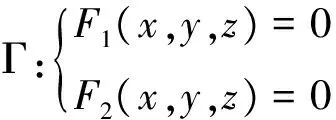
(3)

其中k,r为参数，要想此组平行圆叠加生成所求的旋转曲面，就必须使此组平行圆与母线Γ相交，由(3)与母线Γ的方程可得到关于参数k,r的关系式G(k,r)=0，此式G(k,r)=0与(3)联立便可消去参数k,r，即可得到所求旋转曲面的方程F(x,y,z)=0。

两种解法都是运用平行圆叠加生成旋转曲面的思想，不同点就是：解法1是运用圆心在旋转轴上且过母线上任一点的平行圆，让此点遍历整个母线而叠加生成旋转曲面；解法2则是运用圆心在旋转轴上的平行圆，其大小未定，让此组平行圆与母线相交，也就是确定平行圆的大小后叠加生成旋转曲面。

解法1 设M1(x1,y1,z1)是母线上一点，则过M1(x1,y1,z1)的纬圆方程是

由于M1(x1,y1,z1)在母线上，所以有x1=y1且z1=1，消去x1,y1,z1得所求旋转曲面的方程为

x2+y2+z2-2xy-2yz-2xz+2x+2y+2z-3=0

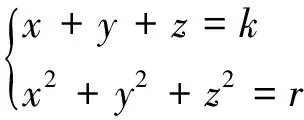
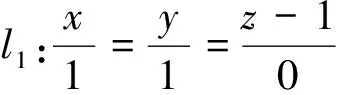
得(x+y+z)2-2(x+y+z)-2(x2+y2+z2)+3=0,

所求旋转曲面的方程即为x2+y2+z2-2xy-2yz-2xz+2x+2y+2z-3=0 .

2.2 当旋转轴为某一坐标轴时的求法

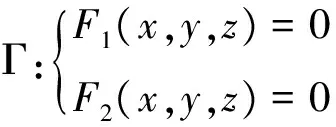
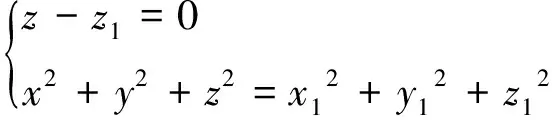
x2+y2=x2(z)+y2(z)即为所求的旋转曲面的方程。

以其它坐标轴为旋转轴，可同样解决。

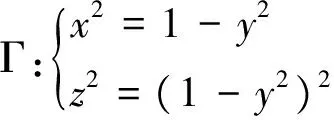
x2+z2=(1-y2)+(1-y2)2, 即x2+z2=(1-y2)+(2-y2)

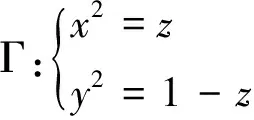
x2+y2=z+(1-z), 即x2+y2=1(0≤z≤1)

当然，也可由2.1的两种解法解出。

2.3 当旋转轴与母线共面时的求法

这时的母线一定是平面曲线，设旋转轴与母线在某一坐标面上，若旋转曲面的母线为

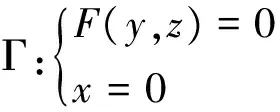
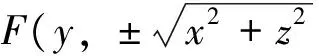
对于旋转轴与母线在其它坐标面，旋转轴为其它坐标轴时，可类似得到旋转曲面的方程。

同理可证明其他形式的结果。

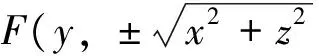
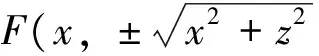
因此，为了方便，求一条平面曲线绕这个平面内的一条直线旋转产生旋转曲面的方程时，总可取此平面为某个坐标平面，此直线为这个坐标面的某一坐标轴建立空间直角坐标系，从而得出旋转曲面的方程。由于旋转曲面的经线也可作为母线与原母线生成同一旋转曲面，故此求旋转曲面的方程的方法也是常用的。

注意 2.2和2.3求旋转曲面的方程时，一定要注意前提条件。

[1]吕林根.许子道.解析几何[M].北京:高等教育出版社.2006.

[2]吕林根.解析几何学习辅导书[M].北京:高等教育出版社.2006.

[3]杨 静.旋转曲面及其方程[J].高等数学研究，2005，8:24～25.

Rotation surface equation

HUANG Zhen-hua1,ZHU Qiu-wen2,HU Qing-hua3

(1.School of Mathematics and Statistics,Hubei Normal University,Hubei Huangshi,435002;2.College of physics and Electronic Science,Hubei Normal University,Hubei Huangshi,435002;3.No.14 Middle School of Huangshi city,Hubei Huangshi,435002)

Solving rotation surfaces equation is a puzzled problem for freshman. This article discuss the solving methods for different positions of rotation axis of rotation surface and generatrix.

rotation surface;rotation axis;generatirx;equation

2016—06—16

黄振华(1960— )，湖北黄石人，副教授，主要研究方向为几何.

O182.2

A

2096-3149(2017)02- 0083-04

10.3969/j.issn.2096-3149.2017.02.018