带有潜伏期的禽流感模型的定性分析

陈 瑶，孙法国，吴梦媛

(西安工程大学 理学院，西安 710048)



带有潜伏期的禽流感模型的定性分析

陈 瑶，孙法国，吴梦媛

(西安工程大学 理学院，西安 710048)

根据实际情况，在禽流感模型中考虑了人类染病后具有潜伏阶段的情况，建立了禽类和人类间传染的禽流感传播模型，研究模型的全局性态.得到了模型的基本再生数，利用V函数、极限方程理论等方法对此模型进行了稳定性分析.证明了当基本再生数不大于1时，无病平衡点全局渐近稳定；当基本再生数大于1时，地方病平衡点全局渐近稳定.

V函数；极限方程；全局稳定性；禽流感模型

众所周知，禽流感在从禽类传染给人类的传播过程中是有潜伏期的，例如，H7N9型禽流感在人体内的潜伏期一般为一周左右.疾病潜伏期的存在使得对疾病的治疗带来了一定的难度.故在禽流感模型的研究中对人类考虑具有潜伏者类，更贴合禽流感传播的实际情况，这对禽流感传播的研究具有重要意义[1-6].

对于禽流感模型的研究已有了一些研究结果[7-11].文献[7]基于饲养业实际，研究了一类染病者即刻被隔离的SEQS禽流感模型，得到了正平衡点的全局稳定性.文献[8]建立了一类带有预防接种的禽流感模型，并考虑了禽类和人类间传染.文献[9-10]考虑了带治疗的禽流感模型.文献[11]考虑了禽流感通过染病禽类和患病人类两种方式传染给易感人类的情况，得到了两类模型平衡点的全局稳定性.文献[12-14]考虑了具体的疾病，H7N9型禽流感，研究了媒体报道对H7N9型禽流感传播的影响.

本文在已有文献的基础上，考虑人类患病后具有潜伏期的情况.

1 模型的建立

根据禽流感的传播特点，禽流感是禽类先携带这类病毒，然后人类染病，故模型从禽类和人类两方面考虑，且人类染病后不会人与人之间传播.把禽类分为易感者，染病者两类，分别用S1,I1表示；把人类(如饲养员、近期宰杀销售等接触禽类的居民)分为易感者，潜伏者，染病者，恢复者四类，分别用S2,E2,I2,R2表示.建立带有潜伏期的禽流感传染病模型：

(1)

禽流感传染给人类的一个重要途径是禽类分泌物或粪便里的高致病性病毒，因此假设人类因接触到禽类染病者I1而受感染，进入潜伏期，人类潜伏者类具有一定的发病率.A1，A2分别为禽类与人类的输入率，θ1，θ2为禽类与人类的自然死亡率，α1是传染易感禽类的传染率，ε2是人类的发病率，β1，β2分别为禽类与人类的因病死亡率，μ为人类对染病禽类的捕杀率，λ1是患病禽类传染易感人类的传染率，γ2是患病人类的恢复率，我们假定所有参数是正常数.

可以看出，模型(1)的动力学性态等价于模型

(2)

由模型(2)前两个方程知，(S1+I1)′=A1-θ1S1(β1+θ1+μ)I1≤A1-θ1(S1+I1)，

由模型(2)后三个方程知，

(S2++E2+I1)′=A2-θ2S2-θ2E2-(β2+θ2+γ2)I2≤A2-θ2(S2+E2+I2)

故系统(2)所有解均要进入

因此，有下面的引理：

引理1 集合是系统(2)的正向不变集.

下面将在不变集中讨论系统(2)的解的性态.

2 基本再生数

令x=(I1,E2,I2mS1,S2)T，模型(2)可写成

x′=F(x)-V(x)，

3 平衡点的存在性

证明：无病平衡点前面在计算基本再生数时已算，同样令系统(2)右端为0，可得

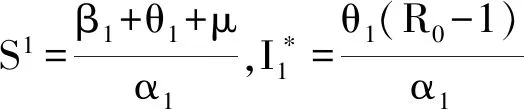
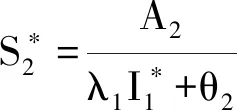
易得，地方病平衡点仅在R0>1时存在.

4 平衡点的稳定性

定理2 对于系统(2)，当R0≤1时，无病平衡点是全局渐近稳定的，当R0>1时，无病平衡点不稳定.

证明：系统(2)在无病平衡点的Jacobian矩阵为

下面证明无病平衡点的全局稳定性.

构造Liapunov函数V=I1，则

由Lasalle不变原理[16]可知，当R0≤1时，无病平衡点P0是全局渐近稳定的.

对于系统：

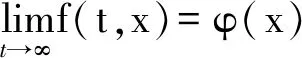
证明：首先考虑系统(2)中的禽类子系统：

可知，当R0>1时，该子系统的地方病平衡点全局渐近稳定.

即，

故可得系统(2)的极限子系统：

解得：

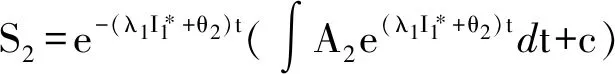
I2=e-(β2+θ2+γ2)t(∫ε2E2S2e(β2+θ2+γ2)tdt+c)

则当t→+∞时，

5 结 语

本文在禽流感传播模型中考虑了人类染病后具有潜伏阶段的情况，建立了禽类和人类间传染的禽流感传播模型，对模型进行了动力学性态分析.得到了禽流感流行与否的阈值，并利用V函数、极限方程理论等方法证明模了模型平衡点的局部与全局渐近稳定性.当R0≤1时，系统只存在无病平衡点，且为全局渐近稳定，这表明禽流感在人类与禽类中都不会流行而且最终会灭绝；当R0>1时，除无病平衡点外，模型还存在地方病平衡点，且此时无病平衡点是不稳定的，而地方病平衡点是全局渐近稳定的，这表示禽流感无论在禽类还是人类中都会流行并且最终将成为一种地方病.因此，为了避免禽流感的进一步流行，必须减小R0的值，有效的方法是通过宰杀禽类来缩短染病期，同时加强对禽类输入者的检疫，必要时停止禽类输入.除此外，提高医疗卫生水平，从而提高治愈率以及加强人们的预防意识也是十分重要的.

[1] 孙小科, 马草川. 一类具有潜伏期的传染病模型的稳定性研究[J]. 生物数学学报, 2014, 29(4): 663-667.

[2] 章培军, 李维德, 李自珍, 等. 具有连续预防接种的双线性接触率的SEIQR流行病模型的定性分析[J]. 兰州大学学报:自然科学版, 2009, 45(4): 118-120.

[3] 胡新利, 周义仓. 具有潜伏和隔离的传染病模型的全局稳定性[J]. 生物数学学报, 2009, 24(3): 461-469.

[4]LIMY,MULDWNEYJS.GlobalstabilityfortheSEIRmodelinepidemiology[J].MathBioSci, 1995, 125(2): 155-164.

[5] 李建全, 马知恩. 两类带有确定潜伏期的SEIS传染病模型的分析[J]. 系统科学与数学, 2006, 26(2): 228-236.

[6] 闫 萍, 吴昭英. 具潜伏期的无免疫型传染病动力学的微分模型[J]. 生物数学学报, 2006, 20(1): 1-10.

[7] 陈永雪. 一类禽流感模型的全局稳定性[J]. 数学的实践与认识, 2012, 42(3): 119-125.

[8] 白 京, 李桂花. 基于禽流感的一类模型建立与性态研究[J]. 数学的实践与认识, 2013, 43(18): 287-291.

[9] 郭树敏, 姚 峰, 李学志. 一类具有治疗的禽流感模型分析[J]. 数学的实践与认识, 2015, 45(1): 192-196.

[10] 郭树敏, 郭丽娜, 李学志. 具有饱和治疗的禽流感动力学模型的研究[J]. 数学的实践与认识, 2010, 40(03): 134-137.

[11] 殷其琴, 冯光庭, 张兴安. 两类禽流感模型的动力学分析[J]. 应用数学, 2015, 28(3): 81-489.

[12] 胡新利, 杨亚莉, 赵惠文, 等. 媒体报道对禽流感(H7N9)传播影响的研究[J]. 西北大学学报:自然科学版, 2014, 44(04): 525-528.

[13] 陈 瑶, 孙法国, 胡新利, 等. 带有媒体报道的H7N9传染病模型的研究[J]. 应用数学进展, 2015, 4(3): 285-291.

[14] 陈 瑶, 孙法国, 胡新利, 等. 含有媒体影响的禽流感(H7N9)模型的定性分析[J]. 纺织高校基础科学学报, 2015, 28(4): 408-412.

[15]DRIESSCHEPVD,WATMOUGHJ.Reproductionnumberandsub_thresholdendemicequilibriaforcompartmentalmodelsofdiseasetransmission[J].MathematicalBiosciences, 2002, 180(1-2): 29-48.

[16]LASALLEJP.Thestabilityofdynamicalsystems[M].Philadelphia:SIAM, 1976. 49-78.

[17]THIEMEHR.ConvergenceresultsandaPoincare-Bendinsontrichotomyforasymptoticallyautomousdifferentialequations[J].JMathBiol, 1992, 30(11): 755-767.

A qualitative analysis of avian influenza model with latent period

CHEN Yao, SUN Fa-guo, WU Meng-yuan

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

According to the reality, a dynamics model of the avian influenza transmission was established in the article to investigate the circumstances of infected human with latent period, and the basic reproduction number of model was obtained. The stability of the model had been analyzed by using V function and the limit equation theory. Proved that the disease free equilibrium was globally asymptotically stable if basic reproduction number was not larger than 1. The epidemic equilibrium was globally asymptotically stable if basic reproduction number was larger than 1.

V function; limit equation theory; globally stability; avian influenza model

2016-08-15.

陕西省教育厅自然科学专项基金资助项目(2013JM1002)

陈 瑶(1991-)，女，硕士，研究方向：常微分方程及其应用.

孙法国(1960-)，男，硕士，教授，研究方向：常微分方程及其应用，生物数学.

O175

A

1672-0946(2017)03-0336-04