飞机飞行参数数据预处理方法研究
2017-06-22金慧琴王正磊胡文春
金慧琴,王正磊,胡文春
(1.海军航空工程学院,山东 烟台 264001;2.92074部队,浙江 宁波 315000)
飞机飞行参数数据预处理方法研究
金慧琴,王正磊,胡文春
(1.海军航空工程学院,山东 烟台 264001;2.92074部队,浙江 宁波 315000)
飞行参数数据的处理对飞机的飞行安全至关重要,而飞行参数数据的误差会显著影响飞行参数数据处理的结果。分析飞行参数数据误差的基本组成,研究飞行参数数据误差中非常规误差的消除方法,给出了四种适用于对不同类型飞行参数数据进行异值剔除与缺失数据估计的方法,仿真结果表明这四种方法大大提高了飞行参数数据的有效性,使飞行参数数据后期处理更便利。
飞参数据;数据处理;异值剔除
飞机在飞行过程中,机载飞行参数记录器实时记录大量的飞行参数数据,在飞行结束后,可对记录器中记录的飞行参数数据进行分析,确定飞机的状态,其结果是再次飞行的依据,对飞机的飞行安全至关重要[1-2]。飞行参数数据的记录过程中,受采集设备故障和随机因素的影响,会造成错误记录,这些错误记录成为误码;同时环境因素的变化和干扰也会引起异常值的出现。因此,在使用飞行参数数据之前,还须对其进行预处理以提高数据的有效性[3]。本文通过分析不同数据的误差来源,针对不同类型和情况的飞行参数数据误差,给出了四种不同的方法对飞行参数数据进行了异值剔除和缺失值的估计。
1 飞行参数数据误差分类
飞行参数数据的误差会明显地影响飞行参数数据处理的结果,尤其在分析飞机不稳定状态的时候,飞行参数数据的误差主要分为随机误差、非常规误差、系统误差、处理误差四种[4]。
1.1 随机误差
随机误差是指由于在测定过程中一系列有关因素微小的随机波动而造成的具有相互抵偿性的误差。随机误差是飞行参数误差中较为常见的一种,由一些微弱因素和未知因素造成,例如飞机零部件的细微变形、数据传输线路的细微影响等。随机误差无法进行预测,但统计特性在设定时间段内是已知的,因此可以通过大量采集数据的方式进行研究,获取统计规律。
1.2 系统误差
系统误差是指由于仪器结构不完善、仪器未校准、本身理论近似性、测量方法不好或测量者生理特点等原因造成的误差。系统误差由系统本身的设计条件和工作状况决定,例如随地球经纬度变化的磁场,随发动机转速变化的排气温度等。系统误差可以用于检测故障,根据实测数据与期望数据之间的偏差情况,可以发现存在的异常并进行判读。系统误差始终对测量造成影响,具有较强的规律性,通常可以使用函数近似表示,便于通过数学方法进行消除。
1.3 非常规误差
非常规误差是指由于特殊条件或者突发故障造成的严重误差。非常规误差一般由外界干扰造成,是飞行参数数据中间断点和异常值的主要来源,例如电子战干扰、线路接触不良等。非常规误差没有固定规律,也难以掌握统计特性,其突发性和严重性容易引起数据“阶跃”或系统故障。
1.4 处理误差
处理误差是指由于数据采集和处理方法的固有缺陷或者操作不当造成的误差。处理误差主要在数据分析处理时产生,例如试验数据的编译码误差和一次处理误差等。处理过程中采用的不同算法自身存在固有缺陷,编译码过程存在误码率,导致处理误差无法消除,但可以通过数据分析总结出一定的规律。
2 飞行参数数据误差的预处理方法
本文所研究的误差消除,主要是上述误差中不满足统计特性的数据,包括非常规误差和其他误差中统计特性不明显的部分,这些数据称为异值。下面给出飞行参数数据异值剔除和参数估计的四种方法。
2.1 增量法
该方法主要针对一些有确定边界的连续信号进行处理,消除那些偏离正常值较大的异值,只是针对飞行参数数据的粗处理[4-5]。
对连续信号f(t),其离散序列f(tk)的增量
Δfk=f(tk)-f(tk-1)
(1)
有界,即存在常数Δ使对于任意的k,有
|f(tk)-f(tk-1)|≤Δ
(2)
据此,可取一正数Δf,简记f(t)的序列f(tk)为fk,对其异常值作如下判断:
如果|fk-fk-1|>Δf,|fi+1-fi|>Δf及|fk+1-fk-1|<2Δf,则判断fk是单重异值;
如果|fk-fk-1|>Δf,|fi+2-fi+1|>Δf,及|fk+2-fk-1|<3Δf,则判断fk、fk+1是二重异值;
如果|fk-fk-1|>Δf,|fi+3-fi+2|>Δf,及|fk+3-fk-1|<4Δf,则判断fk、fk+1、fk+2是三重异值。
异值的替换采用线性插值法,具体描述如下:
对于单重异值fk的替换为:
(3)
对于二重异值fk、fk+1的替换分别为:
(4)
(5)
对于三重异值fk、fk+1、fk+2的替换分别为:
(6)
(7)
(8)
然而Δf的确定并非易事,一般选取
(9)
其中s>0是一常数,而
(10)
在非交叉滑动区间,单一、双重、三重误差可依据上述方法逐次进行修正。
飞行参数数据非常规误差消除的仿真结果如图1所示,采用以上算法可消除飞行参数数据中存在的单一、双重、三重非常规误差。

图1 飞行参数数据的非常规误差消除
2.2 差分法
用多项式逼近一连续函数是一种函数逼近的常用方法,在实际的数据分析和处理的许多插值和滤波方法中有所应用。n次多项式的一项重要性质是其n+1阶导数恒为零,以此得出一种处理飞行记录数据中确定信号的近似方法[6]。假设可用n-1次多项式去逐段近似函数f(t),f(tk)为其离散值序列,其n阶差分
(11)
其中
(12)
于是对于记录数据序列
fk=f(tk)+ηk
(13)
式中,ηk为误差,其n阶差分为
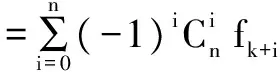
(14)
由此可知,ξk是ηk的n阶差分的一个近似。据此,可作出ηk的n阶差分序列方差的一个估计:
(15)
假设ηk服从正态分布,那么由统计学可知对于0.05的假设检验显著水平,当
(16)
时,可判定ξk是异常值,又由ξk的定义得出fk,fk+1,…,fk+n中有一个异常值。根据经验以及ξk本身的定义,当判定ξk异常时,相应地判定fk+n/2(n为偶数)或fk+n/2和fk+n/2+1(n为奇数)为异常值较为合理。
依据上述方法,异常值仍然可以被判定为二重、三重。仅以至多三重异常值为限,对于更多重的可以用分组的方法进行。差分法是一种统计处理的方法,判断比较准确,异常值的剔除相较增量法更为精确。
2.3 稳健异值检测与修复方法
对于飞机的气动参数,在飞行参数数据处理时要求有更高的精度,在实际数据的异常值处理中,经常遇到门限值的选取影响异常值的判断问题。当外推值与观测值的差值在门限附近变化时,就难以决断是否把它们按照异常值处理[7]。针对这种“拖尾”的正态分布含斑点异值的数据,提出一种“抗干扰”的估计方法,即稳健估计。通过稳健的线性模型系数辨识法,逐点进行异值的辨识与修复[8]。
假定某一飞行参数数据集合为
D={f(t1),…f(tn)}
(17)
由于目标运动的连续性,可以假定测量对象f(t)可合理地分解成3部分:
f(t)=ftr(t)+εs(t)+ε0(t)
(18)
式中,ytr(t)称为趋势分量,描述的是参数的趋势项,εs(t)是数据随机误差分量,ε0(t)为过程的污染分量或突变性分量,其作用结果是使数据发生严重偏离。
假定:在有限时段上,气动参数符合的函数f(t)是几乎处处连续、按段光滑的,可以被代数多项式与三角多项式的线性组合一致逼近,即

εs(t)+ε0(t)
(19)
其中,T为周期性变化分量fp(t)的演变周期。
改写为线性回归模型的形式:
(20)
式中,
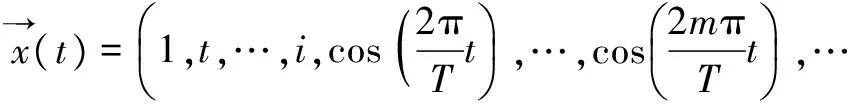
(21)
β=(a0,a1,…,al,bi,…,bm,c1,…,cn)T
(22)
ε(t)=εs(t)+ε0(t)
(23)
下面给出估计方程(20)的一组迭代求解算法[9]:
(24)
并置初值为:
(25)
(26)
在数据预处理时,经常使用下列几种φ(w)函数。
Huber型:
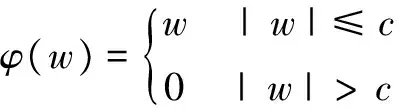
(27)
hampel型:
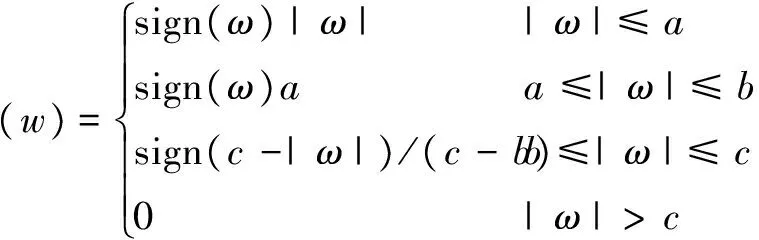
(28)
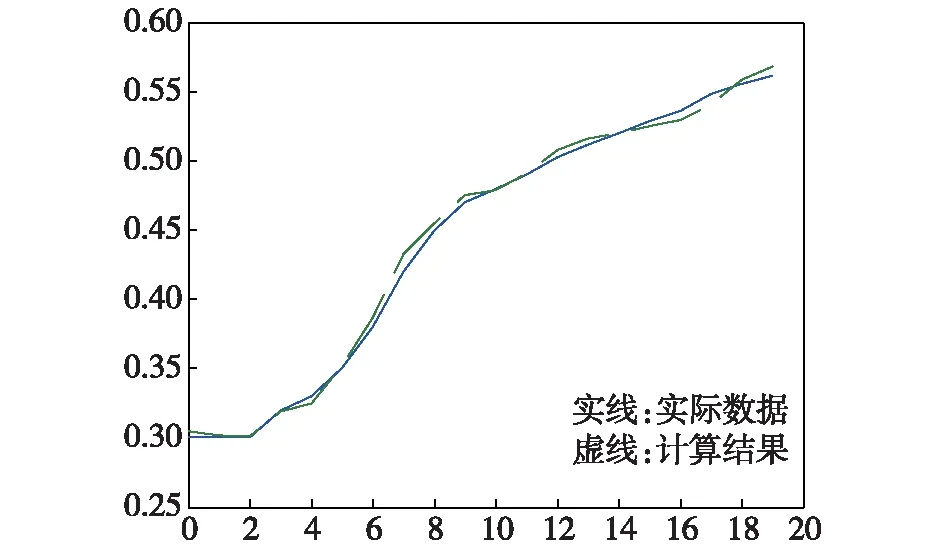
式中,0 1)首先根据数据规律构造一条具有稳健特性的平滑函数(确定模型、阶次)。 2)选取基准段,一般为初始段,计算出基准段σ。 3)用稳健预测基准段中点的状态值,与实际量测值比较,根据似然比检验原理,若估计值和实际测量值的绝对值相差小于3σ~5σ,认为量测值为合理值。 4)如果相差大于3σ~5σ,则认为是异值。对于中点状态以后的点,估计值和实际值大于固定门限(提前设定的非负值)则认为是异值。异值用稳健估计值代替。 5)基准段更新。去掉原基准段的第一个值,并补以基准段后紧邻的第一个值(如果测量值已被判为异值,则补以它的稳健估计值),即基准段向后移动一个点。如果整个数据处理完毕,则运算完毕,否则,转向3)。 在仿真过程中采用下述“多项式+正态测量误差”模型[10]: y(t)=b0+b1t+b2t2+ε(t)ε(t)~N(0,0.25) (29) 并设定参数b0=60,b1=15,b2=0.5,然后在45~50设定偏差均值为2的正分布误差、90~96设定为偏差为20的错点,采用上述仿真数据进行估计,同时给出了模型系数的全点稳健估计以及常用的最小二乘估计,效果如图2所示。 图2 最小二乘估计、稳健估计效果对比 从图2(a)、图2(b)的比较中可明显地看出,稳健估计不包含仿真模型的趋势分量,具有良好的抗异值能力。 2.4 基于参数间函数关系的参数缺失估计法 在一个较长的时间段内,某个飞行参数没有被记录,而同时其它飞行参数则记录完整时,如果缺失的飞行参数与其它被正常记录的飞行参数之间存在确定的函数关系,则利用这种函数关系,可估计出缺失的飞行参数。由于在飞行事故调查时特别关注飞机进入复杂状态和坠地瞬间的速度和姿态,所以这里给出马赫数、真空速和俯仰角的一种估计方法。 马赫数(M)和真空速Vi的估计: 输入参数:飞行高度(H)、表速(Vi)、大气温度(Ti)。 采用二次多项式近似逼近的方法,首先获得M=f(H,Vi),再由马赫数估计出真空速[4]。 当Vi<500km/h或H<10000m时: (30) 当Vi>500km/h且H>10000m时: (31) (32) (33) 其中,aH为音速,TH为大气静止温度,K为波尔兹曼常数,g为重力加速度,R为气体常数,N为大气总温传感器的品质系数。 图3给出了某型飞机在完成某动作过程中的马赫数的估计结果,飞行参数数据来自于机载飞行参数记录器。图中实线为飞行参数数据记录器实际的记录值,虚线为利用上述公式估计的马赫数,二者最大估计误差为0.013。 图3 马赫数的估计结果 本文分析了不同数据的误差来源,同时针对不同类型和情况的飞行参数数据误差,运用四种不同的方法对飞行参数数据进行了异值剔除和缺失值的估计并分别对数据处理的效果进行了仿真,结果表明这四种 方法大大提高了飞行参数数据的有效性,为后续飞参数据的快速和详细处理提供了正确有效的数据源。 [1] 刘海波,李国柱,赵峰.飞行记录系统发展概况[J].运输机工程,2002(124):19-21. [2] 张鹏,张建业,李学仁.飞行数据趋势监测在飞机“健康状况”评估中的应用[J].空军工程大学学报(自然科学版),2004,5(3):8-10. [3] 杨全法,任章,董伟凡.飞行事故调查中的飞行数据记录器译码分析技术[J].航空维修与工程,2004(5):40-42. [4] 倪世宏,史忠科,谢川,等.飞行事故调查时缺失飞行参数的综合估计方法[J].计算机工程与应用,2004(32):206-209. [5] Й.М.巴施柯夫斯基,Б.А.列奥诺夫,Б.К.巴普拉夫斯基.飞机飞行试验及试验结果的处理[M].北京:航空工业出版社,1991. [6] 曾小波.飞行数据误码与野值的剔除[J].飞行试验,1995,11(3):29-33. [7] 林兆福,王书元,李光辉.飞行状态数据的有效性检查[J].中国民航学院学报,1996,14(4):1-7. [8] Civil Aviation Authority. Approval, Operational Serviceability and Readout of light Data Recorder Systems[M/OL]. http:∥www.caa.co.uk.. 2004. [9] Vladislav. Clein. Estimation of Aircraft Aerodynamic Parameters From Flight Data[J]. Prog. Aerospace Sci. 1989, 26(1): 1-77. [10]Neil Campbell. Flight Data Analysis Using Limited Data Sets[Z]. Gold Coast, Australia. ISASI. 2004. A Research on Preprocessing Methods of Flight Data JIN Hui-qin, WANG Zheng-lei, HU Wen-chun (1.Naval Aeronautical and Astronautical University, Yantai 264001;2.92074 Unit, Ningbo 315000, China) The processing of flight data is very important for the aircrafts’ safety. However, error on flight data can significantly influence the processing results. On analyzing the basic compositions of error on flight data and the elimination methods of unconventional error on flight data, error is classified and four methods of different values rejection and missing data estimation are presented according to different type flight data. The result of the simulation shows that the four methods greatly improve the effectiveness and can be convenient for post-processing of flight data. flight data; data processing; values rejection 2017-03-07 金慧琴(1964-),女,硕士,副教授,研究方向为通信与导航。 王正磊(1992-),男,硕士研究生。 胡文春(1975-),男,高级工程师。 1673-3819(2017)03-0121-05 TP391;E917 A 10.3969/j.issn.1673-3819.2017.03.026 修回日期: 2017-03-29

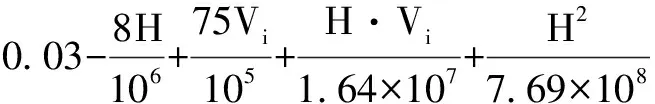

3 结束语
