基于动态贝叶斯网络的空战决策方法

2017-06-22孟光磊罗元强徐一民

指挥控制与仿真 2017年3期

关键词：空战贝叶斯机动

孟光磊,罗元强,梁宵,徐一民

(1.沈阳航空航天大学，辽宁沈阳 110136；2.西北工业大学，陕西西安 710129)

基于动态贝叶斯网络的空战决策方法

孟光磊1,罗元强1,梁宵1,徐一民2

(1.沈阳航空航天大学，辽宁沈阳 110136；2.西北工业大学，陕西西安 710129)

针对无人机高强度空战对抗问题,开展智能决策方法研究。分析了目前无人机空战决策方法的研究进展,总结了影响空战决策方法适用性的主要原因。针对空战决策的实时性和不依赖飞机运动学模型的需求,提出了基于DBN的无人机空战决策模型。综合分析无人机可以获得的机载传感器和情报信息,从中提取出影响无人机机动决策结果的态势因素,依据各因素间的因果关系,建立了无人机空战决策模型的网络拓扑结构。阐述了网络模型有向弧条件概率表、决策节点状态转移概率的设计思路。设计了网络决策模型的前向递归推理算法,并进行了算法复杂度分析,分析表明算法时间复杂度在可接受的范围内,能够满足工程应用的要求。最后,开展典型战场态势下的单机对抗仿真实验。仿真结果验证了决策网络的适用性以及推理算法的收敛性和实时性,表明动态贝叶斯网络空战决策模型提高了无人机机动决策的有效性和灵活性。

无人机;空战决策方法;DBN;前向递归推理算法;概率推理

近年来,无人机在军事领域的应用,受到研究人员较多关注。目前,学者们提出了多种应用于空战决策的方法。文献[1]在假设飞机运动学模型已知的基础上,建立了无人机追逃的微分对策模型,并进行了对抗仿真。文献[2]开展了基于智能微分对策的自主机动决策方法研究,通过预测对抗双方的运动状态,将双边极值问题转化为单边极值问题, 从而能够对空战对抗过程中的机动决策进行求解。文献[3]提出了一种基于评分函数矩阵的微分对策方法,并将该方法用于解决空战过程中的机动决策问题。基于微分对策求解空战决策问题的方法存在一个共同特点,即假设双方战机在博弈环境中的运动学模型已知,才能求得战机运动的优化解决方案。文献[4]提出采用滚动时域方法预测空战态势在未来一段时间内变化,在此基础上采用最优控制方法求解能使无人机获得最大攻击优势的控制序列。文献[5]提出基于MTPM和DPM的多无人机协同滚动时域决策方法,用于解决多机协同决策问题。上述滚动时域方法通过预测敌机运动轨迹,对未来的博弈态势进行预判,作为己方机动决策的依据,是让无人机在将来一段时间取得空间占位优势的有效策略。提高预测的准确度是提升这类决策方法有效性的关键。文献[6-7]在影响图的理论基础上进行不确定性空战机动决策建模,但考虑的因素较少,没有通过全局态势观测数据构建决策模型。文献[8]提出了近似动态规划空战决策方法,先对空战对抗结果进行离线学习,然后根据学习结果进行在线决策,解决了空战决策的实时性问题。上述研究从人工智能角度对空战过程机动规划问题进行了有益的探索,为未来空战决策系统在工程上的实现提供了理论方面的参考。

战机飞行员在空战过程中,通过综合分析各类传感器中获取的战场信息,通过层级化的逻辑推断得到关于战场态势的评判,做出有利于己方的机动决策结果。本文通过一种模拟飞行员思维方式的新视角解决空战决策问题,采用动态贝叶斯网构建无人机机动决策模型,使用条件概率描述各个态势因素间的因果关系。仿真结果表明采用概率关系描述空战决策模型,能够实现在不依赖飞机运动学模型的情况下进行有效的空战决策,具备较好的实时性和环境适应性,能够满足工程应用的需求。

1 基于DBN的单机对抗空战决策模型

动态贝叶斯网络克服了基于规则的系统在时间依赖表达和计算上的困难,采用概率分布描述因果关系,具有强大的不确定性问题处理能力。基于贝叶斯网络的特点和决策系统应用上的优势,建立了基于DBN的单机对抗空战决策模型。

战场态势信息是空战决策的依据,综合分析无人机可以获得的机载传感器和情报信息,作为单机对抗决策模型的观测节点,其状态集定义如表1所示。

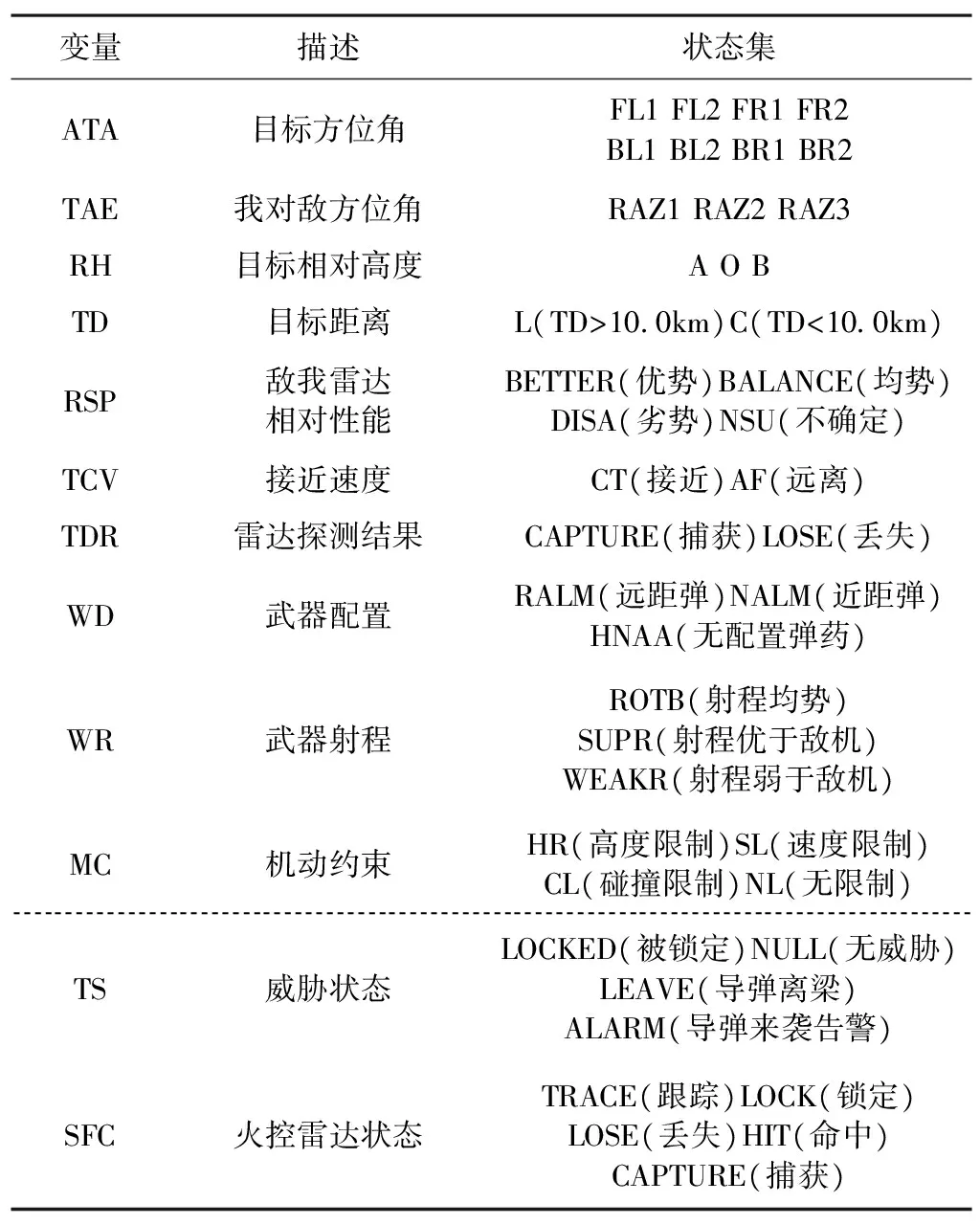
表1 观测节点状态集定义

观测节点中ATA 和TAE描述的是无人机和目标间的方位关系,如图1所示。

图1 目标和无人机间的相对几何关系

考虑空战决策的合理性，为减小计算负荷,以红方无人机位置为坐标原点,对ATA的取值进行离散化,如图2所示。TAE反映了敌机对我机的探测能力以及相对运动趋势,是态势评估的重要证据信息,以蓝机位置为坐标原点,其取值空间划分如图3所示。

图2 ATA取值空间划分

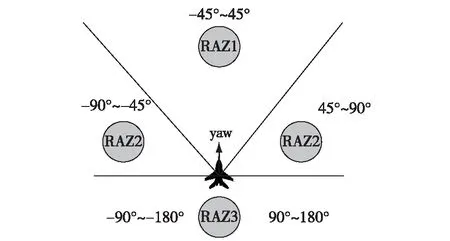
图3 TAE取值空间划分

提取出对决策起关键作用的环境特征,作为决策模型网络的中间节点,定义如表2所示。中间节点作为信息推理的中间层,将观测节点与根节点通过有向弧联结起来,对观测信息做出响应。其中,TB综合目标方位和高度反映了目标所在的空间区域;TSD在TB的基础上又考虑了目标与无人机的距离因素;TSS在TSD的基础上增加了对于敌我接近速度的考量;EDP结合目标距离、方位和敌我雷达相对性能对目标探测性能进行评估;TIN反映了对抗过程中双方的信息态势,是对目标探测性能和无人机雷达探测结果的综合比较结果;WS反映了无人机配置导弹相对于目标的射程优势;SDF是综合态势评估结果,反映了无人机的占位优势和攻击条件准备情况。SDF评估所用到的集合BS中FR、FL、RS、LS、BR、BL分别表示右前方、左前方、右侧方、左侧方、右后方、左后方;集合ATC中AT、UAT、UAC分别表示具备攻击条件、暂不具备攻击条件、无可用弹药。

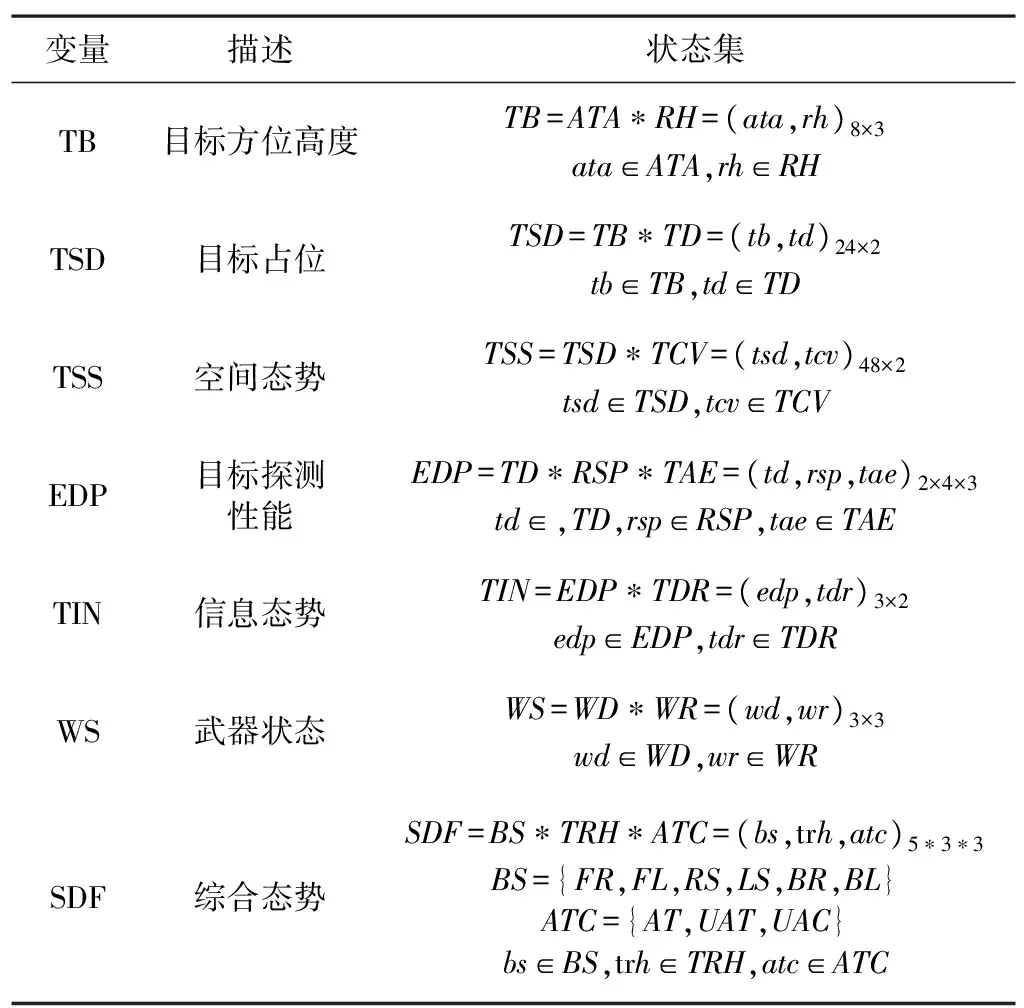
表2 中间节点状态集定义

单机对抗决策模型的输出是无人机选择执行的机动动作, 选取18种飞机典型的基本机动动作为决策节点的状态集,定义如表3所示。

分析空战决策信息间的因果关系,建立基于DBN的单机对抗空战决策模型,如图4所示。网络模型由20个节点组成,其中包括1个决策节点,12个观测节点以及7个中间节点。网络节点间通过有向弧联结,彼此间的依赖程度由对应的条件概率表CPT(Condition Probability Table)决定。DBN网络节点可以在时间上产生相互联系,为提高决策结果的收敛速度,空战决策网络前后两个时刻的决策节点通过状态转移概率有向弧联结,网络根据前一时刻的推理结果与当前时刻的证据信息更新决策节点的概率分布。根据动态贝叶斯网络的性质,CPT和状态转移概率可以根据先验知识设定,具备使用客观数据进行学习的扩展性。为验证基于DBN的空战决策网络的可行性,本文根据空战仿真经验对网络参数进行设定。空战决策网络模型推理过程自底向上,逐层提取战场特征,网络参数的设定要保证决策模型有效准确地进行特征提取。每条有向弧的条件概率表对应一个条件概率矩阵,矩阵的行列维数由有向弧父节点和子节点的状态集维数确定。条件概率矩阵中每一个元素的取值根据子节点各状态对父节点状态的影响程度决定。状态转移概率矩阵描述了当前机动决策状态在下一时刻转移到另一机动决策状态的可能性,其概率集中分布在矩阵对角线上,根据各机动决策状态向其它机动决策状态转移的可能性进行状态转移概率设定。

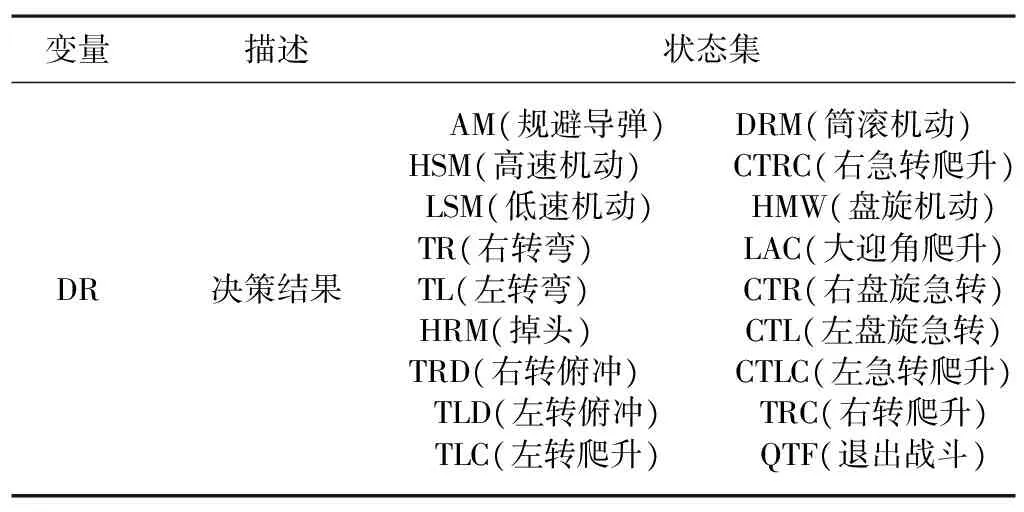
表3 决策节点状态集定义

2 决策模型推理算法

根据单机对抗决策DBN模型,决策推理可表示为在当前观测节点和上一时刻决策结果条件下求解当前决策节点的条件概率分布。采用前向递归推理算法进行决策模型推理,算法设计基于如下定理。

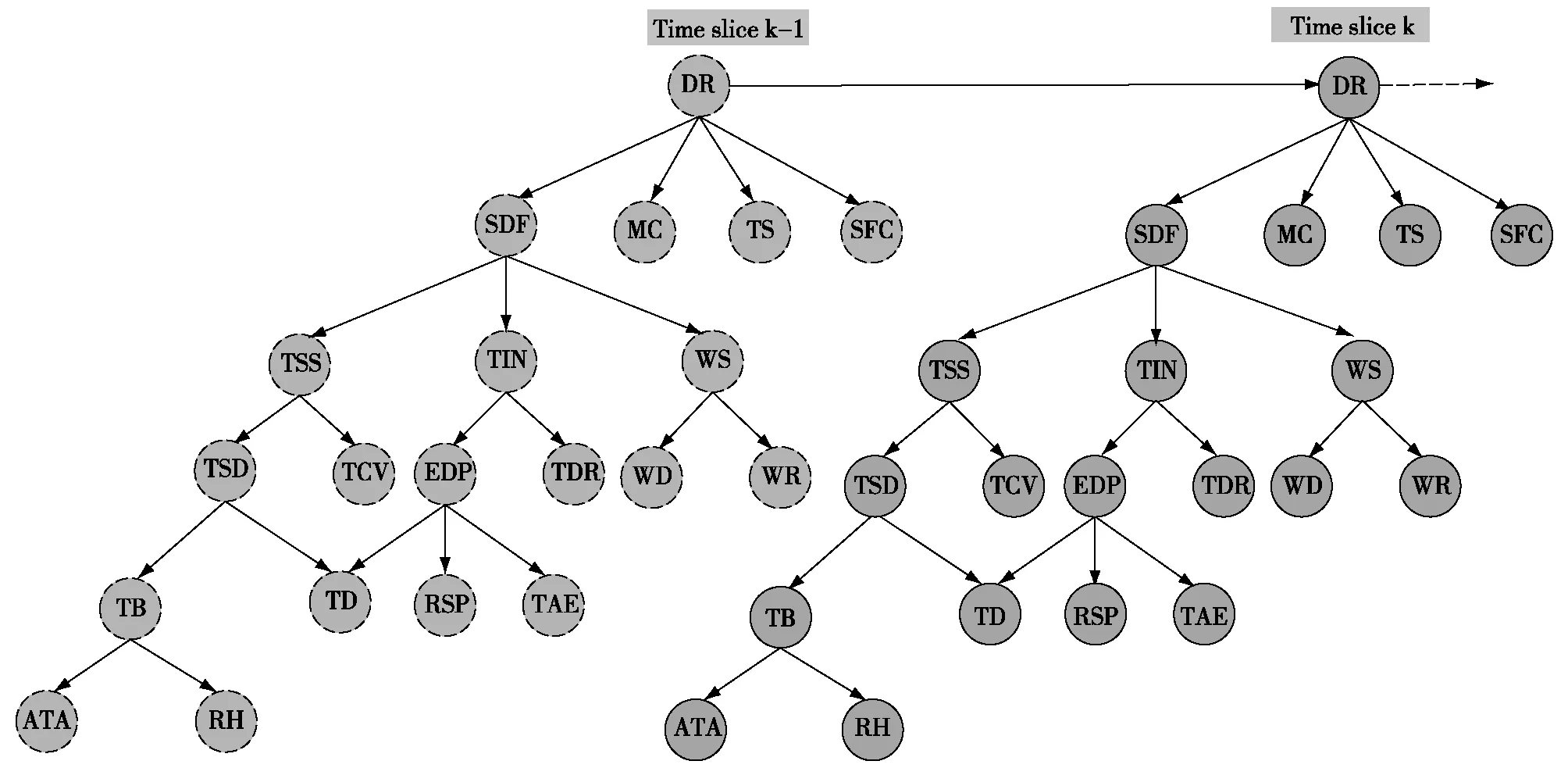
图4 单机对抗空战决策DBN模型

贝叶斯定理:贝叶斯定理是关于随机事件A和B的条件概率,对于随机事件A和B,在事件B发生的情况下事件A发生的概率可表述为

链式规则:链式规则推理是直接利用贝叶斯规则与链中的条件独立性假设展开进行推理。例如在链式网络A→B→C中,根据链式规则有

2.1 前向递归推理算法

单机对抗决策DBN模型为标准HMM(Hidden Markov Model)模型,有滤波、预测以及平滑三种推理方式,本文采用的是滤波推理,其推理过程为:

P(DRt|e1:t)=αP(et|DRt)·

(1)

其中,α为归一化因子,et为t时刻从观测节点采集的证据信息集合,DRt为t时刻根节点取值。算法实现的具体步骤如下。

Step1初始化网络节点的状态集维数，加载先验分布、条件概率分布和状态转移概率。设定网络推理周期的迭代次数为n。Step2根据链式规则和条件独立性假设，依据从观测节点采集到的当前证据信息计算决策节点分布P(DRt|et)。Step3依据贝叶斯定理，使用P(DRt|et)计算条件概率分布P(et|DRt)。Step4根据P(et|DRt)、状态转移概率P(DRt|DRt-1)和上一时刻迭代推理结果P(DRt-1|e1：t-1)，由式(1)计算累积证据信息下的决策节点概率分布P(DRt|e1：t)，完成一次迭代推理。Step5记录迭代次数，并保存P(DRt|e1：t)，以备更新下一时刻决策节点的推理结果。Step6判断是否完成n次递归推理，若未完成转至Step2，否则转至Step7。Step7输出DR节点中概率最大的机动决策结果，重置网络，重复执行Step1到Step7。

对于Step2中P(DRt|et)的计算,根据链式规则和条件独立性假设将全局网络展开有:

(2)

式(2)中从各观测节点到决策节点的对应链路条件概率计算过程相似,以P(DRt|ATAt)计算为例,根据贝叶斯定理和链式规则,结合网络模型拓扑结构可得:

(3)

将全部观测节点到决策节点的对应链路条件概率计算结果代入公式(2),计算得到P(DRt|et)。

(4)

其中P(DRt|et)是Step2的计算结果。

在执行Step 4时,根据公式(1)使用Step 3计算结果计算累积证据信息下的决策节点概率分布,完成一次迭代推理:

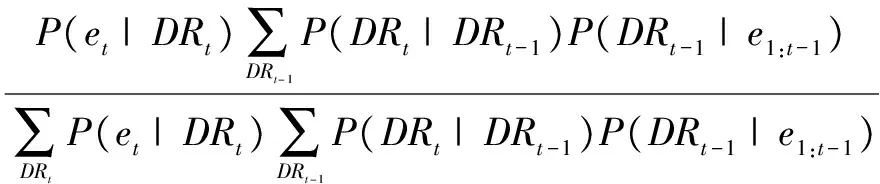
(5)

其中，P(DRt|DRt-1)为状态转移概率，P(DRt-1|e1:t-1)是前一时刻的决策推理结果。

完成Step 5～Step 7,实现n次迭代递归推理后,输出DR节点中分布概率最大的机动决策结果。

2.2 算法复杂度分析

根据各链路推理过程以及网络节点状态数量进行算法复杂度分析。从各观测节点到决策节点的对应链路条件概率计算所需的乘法、加法、除法次数如表4所示。

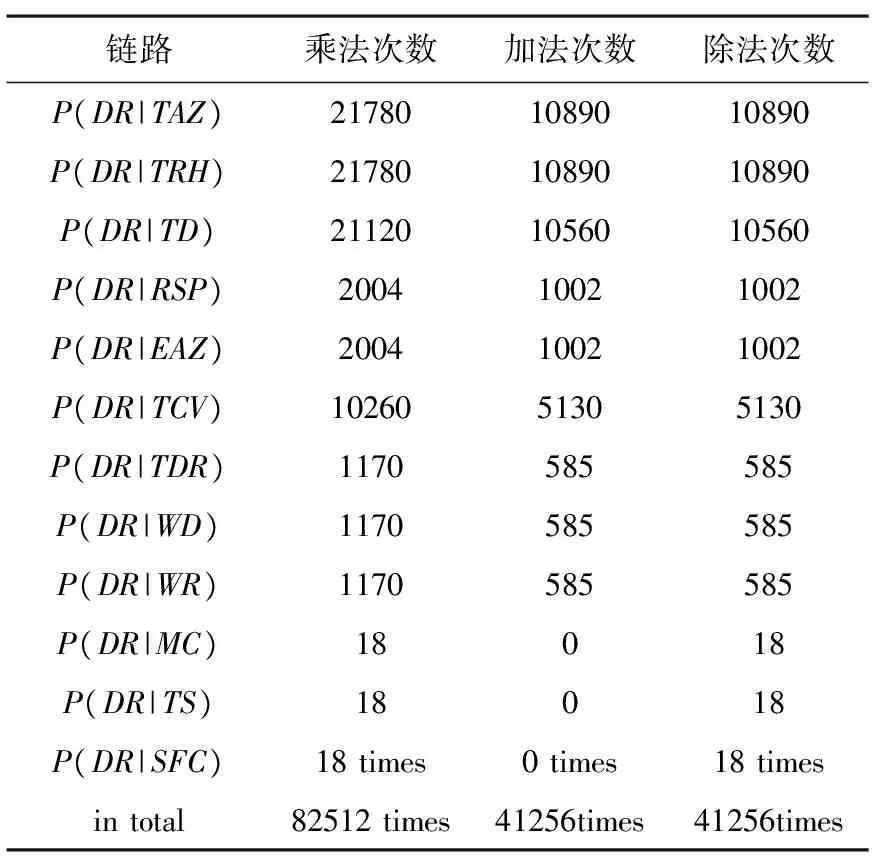
表4 各条链路算法复杂度

分析算法的复杂度可知,算法完成一次迭代需要执行乘法82512次,加法41256次,除法41256次。当迭代次数n取10时,以主频2.8GHz处理器为例,可以在10ms内完成一个决策推理周期计算, 能够满足空战决策的实时性需求。

3 仿真与分析

为验证单机对抗DBN决策模型的有效性,在高强度空战态势下进行了仿真分析。红方根据DBN决策模型的输出进行自主机动决策,蓝方在操纵杆的控制下作任意机动飞行。在仿真过程中，为保证对抗的公平性,并测试决策模型的性能,空战双方采用相同动力学模型仿真,确保双方机动能力相同。同时假设双方信息获取能力和电子战能力相同,且具有相同的武器配置,并保证弹药充足。在这种极限条件情况下验证机动决策网络对高强度空战环境的适应能力。表5为红蓝双方的初始状态信息。初始状态一旦设定,对抗双方则进入自由空战,对抗双方将进入持续缠斗直到任意一方构成攻击条件。缠斗过程中,载机只有在无可用弹药的条件下才会退出战斗,否则将不断进行机动飞行以构成攻击条件。

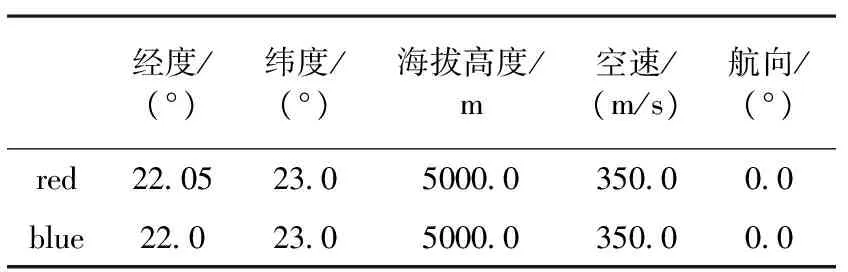
表5 初始态势信息

图5为在决策结果的引导下红方飞机与蓝方飞机的对抗轨迹。红方飞机在决策信息的引导下依次进行右盘旋急转机动(动作号10)、左转爬升机动(动作号16)以及右转机动(动作号6),成功占据了蓝机后方的有利攻击位置。图6为DBN决策模型在每个推理周期输出的红方飞机机动动作序号。图中标记的转折点对应的横坐标是红机机动动作的切换时刻。

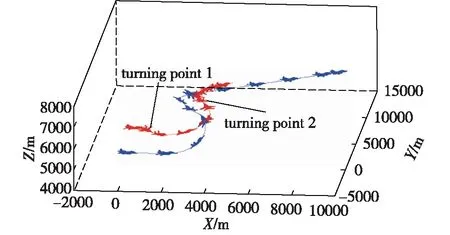
图5 对抗飞行轨迹

图6 DBN决策模型输出

图7-图8为图6中各转折点前后两个推理周期决策节点状态概率分布输出,其中一个推理周期进行10次迭代。从图8中可以看出，在转折点1前决策结果为10号机动动作(右盘旋急转机动),其对应概率随着迭代进行从0.182递增收敛到0.9943;随着态势改变决策结果切换为16号机动动作(右转爬升机动),其概率随着迭代进行从0.2113递增收敛到0.9874。转折点2处的决策节点概率分布结果(图8)也表明网络在观测信息的激励下利用前向递归推理算法进行10次迭代后,决策节点概率向合理的机动决策结果收敛。

图7 转折点1概率分布图

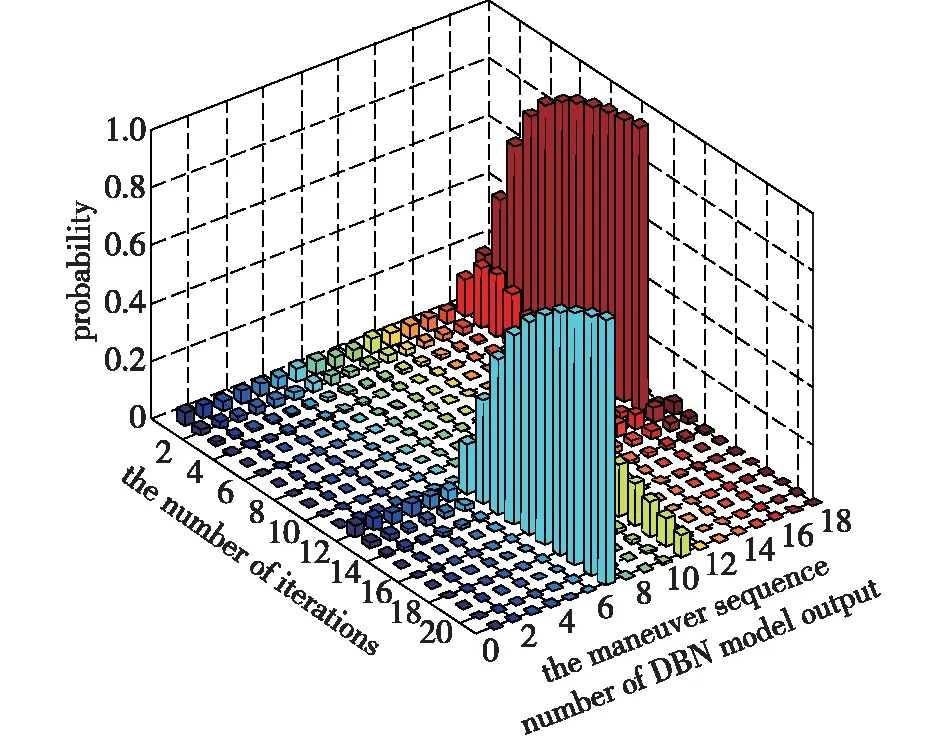
图8 转折点2概率分布

4 结束语

为了模拟空战过程中飞行员的决策思维,从人脑思维习惯角度解决空战决策问题,实现在不依赖于飞机运动学模型的条件下进行有效的空战决策,本文提出了一种基于DBN的空战决策方法。仿真结果表明,基于DBN的空战决策方法使无人机能较好地适应战场环境,可以引导无人机进行有效的自主决策,提高了无人机机动决策的灵活性和有效性。而且,决策网络表现出较快的收敛速度,实时性能够满足工程应用需求。空战对抗环境日趋复杂,尤其在复杂电磁环境中,存在诸多干扰,如何保证决策的可靠性、客观性至关重要。根据动态贝叶斯网络的性质,其网络参数可以根据先验知识设定,也具备使用客观数据进行学习的扩展性。未来将研究根据仿真对抗结果进行网络参数学习

的方法,使得决策模型能够更好地拟合实际战场环境。

[1] 车竞,郑凤麒. 基于微分对策的追逃对抗仿真[J]. 飞行力学, 2014, 32(4): 372-375.

[2] 钟友武,杨凌宇,柳嘉润，等. 基于智能微分对策的自主机动决策方法研究[J]. 飞行力学, 2008, 26(6): 29-33.

[3] Park Hyunju,Lee Byung-Yoon, Tahk Min-Jea. Differential Game Based Air Combat Maneuver Generation Using Scoring Function Matrix [J]. International Journal of Aeronautical and Space Sciences， 2016, 17(2)204-213.

[4] 傅莉,谢福怀,孟光磊. 基于滚动时域的无人机空战决策专家系统[J]. 北京航空航天大学学报, 2015, 41(11):1994-1999.

[5] 沈东,魏瑞轩,祁晓明，等. 基于MTPM和DPM的多无人机协同广域目标搜索滚动时域决策[J].自动化学报,2014, 40(7):1391-1403.

[6] Virtanen K., Raivio T. Modeling pilot’s sequential maneuvering decisions by a multistage influence diagram[J]. Journal of Guidance, Control, and Dynamics,2004, 27(4):665-677.

[7] Zhong Lin., Tong Ming an, Zhong Wei. Sequential maneuvering decisions based on multi-stage influence diagram in air combat [J]. Journal of Systems Engineering and Electronics, 2007, 18(3):551-555.

[8] James S, McGrew, Jonathan P, How. Air-Combat Strategy Using Approximate Dynamic Programming[D]. Journal of Guidance, Control and Dynamics, 2010,33(5): 128-136.

Air Combat Decision-making Method Based on Dynamic Bayesian Network

MENG Guang-lei1, LUO Yuan-qiang1, LIANG Xiao1, XU Yi-min2

(1.Shenyang Aerospace University, Shenyang 110136；(2.Northwestern Polytechnical University, Xi’an 710129, China)

The decision-making method is studied for high-intensity UAV air combat in this paper. The present research progress of the UAV air combat decision method is analyzed. And the main reasons that influence the applicability of the decision method are summarized. For real-time, fault-tolerance, and not relying accurate mathematical model of aircraft requirements, a decision-making model based on DBN is proposed for one-to-one UAV air combat. By synthetically analyzing the information that can be obtained from the airborne sensors and intelligence, the situational factors affecting UAV’s maneuver decisions are extracted and the DBN topology structure is constructed. The design ideas of the directed-arc conditional probability table and decision node state transition probability table of the network model are illustrated. The forward recursive reasoning algorithm for decision-making network model is designed and the algorithm complexity is analyzed. The analysis result indicates that the time and special complexity of the algorithm is acceptable, which could satisfy the requirement of engineering application. Finally, the simulation results verify the practicability of the decision network, and prove the convergence, real-time performance of the reasoning algorithm, the adaptability of network model. The results indicate that Air combat decision model improving the flexibility and validity of the UAV’s maneuver decision.

UAV; air combat decision-making method; DBN; the forward recursive reasoning algorithm; probabilistic inference

2017-03-21

孟光磊(1982-),男,辽宁沈阳人,博士,副教授,研究方向为无人机空战决策。罗元强(1992-),男,硕士。梁宵(1984-),男,博士,副教授。徐一民(1996-),男,本科。

1673-3819(2017)03-0049-06

TJ85；E926.391

10.3969/j.issn.1673-3819.2017.03.011

修回日期： 2017-04-10