一种空间飞行轨迹的大地坐标计算方法

常晓华，丰 海，张 婕，邱亚男

（北京宇航系统工程研究所，北京，100076）

一种空间飞行轨迹的大地坐标计算方法

常晓华，丰 海，张 婕，邱亚男

（北京宇航系统工程研究所，北京，100076）

针对弹道飞行器空间飞行轨迹的大地坐标计算，从弹道计算的地心球坐标出发，给出一种利用空间几何关系的迭代法，避免了地心直角坐标的转换过程。通过与传统算法的对比分析，验证了该算法的有效性，并进一步明确了该算法的迭代初值，分析了该算法在弹道飞行器空间飞行轨迹大地坐标计算中的适用性。

空间飞行轨迹；大地坐标；迭代法

0 引 言

有效性、迭代初值和适用性进行了仿真分析。

随着弹道飞行器精确化控制水平的提升，需要精确计算空间飞行轨迹的大地坐标，传统计算方法要求在弹道计算中给出飞行器的地心直角坐标，进而直接利用大地测量学的相关研究成果，将该问题转化为地心直角坐标与大地坐标的转换问题。

针对地心直角坐标向大地坐标的转换问题，国内外学者进行了大量研究工作，提出了许多算法，基本可以分为迭代法和直接法两类方法[1～9]，在计算的精度和速度上都有了较大提高。但是，这些算法越来越复杂[10]，其成果难以直接用于弹道飞行器空间飞行轨迹的大地坐标计算。

另一方面，已有算法是从大地测量角度出发，而弹道飞行器弹道计算中有其特有的物理参数，对相应的大地坐标计算问题的研究较少。

本文针对弹道飞行器空间飞行轨迹大地坐标计算问题，直接从弹道计算的地心球坐标系分量出发，给出了一种利用空间几何关系的迭代法，并对该算法的

1 地心直角坐标系与大地坐标系

a）地心直角坐标系。

地心直角坐标系与大地坐标系如图1所示。

原点O为椭球中心；Z轴是椭球旋转轴，指向地球自转轴方向；X轴指向起始大地子午面（过格林尼治平均天文台的子午面）与赤道的交点；Y轴与X轴、Z轴构成右手坐标系，-O XYZ称为地心直角坐标系。地面或空间任一点P，可用地心直角坐标（X，Y，Z）表示。

b）大地坐标系。

图1中，P点的坐标还可用大地坐标表示，即经度L、大地纬度B和大地高程H。

c）大地坐标与地心直角坐标的关系。

大地坐标（L，B，H）向地心直角坐标（X，Y，Z）的转换公式为

式中 N=a/(1-e2sin2B)1/2，其中，a为地球椭球半长轴，e为第1偏心率。

由式（1）可导出地心直角坐标向大地坐标的转换公式：

由式（2）可以看出，大地经度可直接求解，而大地纬度和大地高程的计算公式由于相互耦合，无法直接求解。因此，地心直角坐标向大地坐标的转换问题，可以归结为大地纬度和大地高程的解算问题。

2 求解大地纬度和大地高程的常用算法

在众多算法中，经过研究、对比分析，给出3种简单实用的大地纬度和大地高程求解算法，可直接用于弹道飞行器空间飞行轨迹的大地坐标计算。

2.1 直接法

a）椭球面近似法。

椭球面近似法是基于大地高程H较小、P点近似位于地球椭球表面时的假设条件，利用大地纬度和地心纬度及椭球方程式推导得到。大地纬度计算公式为

大地高程的计算公式为

在极区（B接近±90°）附近，改用下式计算：

该方法比较简单，但在大地高程H稍大时，计算精度会急剧下降。

b）Bowring法[5,6]。

在直接法中，Bowring法是一种计算简便且精度较高的算法，通过P点所在子午面内辅助圆与椭圆的解析几何近似推导得到。大地纬度计算公式为

式中 a为长半轴；b为短半轴；2e为第2偏心率。

利用式（5）计算得到B后，再根据式（4）、式（5）计算大地高程H。

该方法虽然计算简单，但形式比较复杂，过程参数物理概念不够直观，给使用者的理解带来了一定难度。

2.2 迭代法

由式（2）可以看出，迭代法是求解大地纬度和大地高程的最直接方法，这里给出应用较多的一种迭代法，本文称为传统迭代法，大地纬度的迭代公式为[1]

经过迭代计算得到大地纬度B后，再根据式（4）、式（5）计算大地高程H。

迭代法通常精度较高，但迭代初值的选择不同，达到某一精度所需的迭代次数也不相同，计算时间也不同。文献[2]、文献[3]中分析了不同迭代初值下的迭代精度和迭代次数。

3 利用空间几何关系的迭代法

通过对以上3种算法及其它算法的分析可知，现有大地纬度和大地高程的解算，均从地心直角坐标系三分量（X，Y，Z）出发。

在弹道飞行器空间飞行轨迹的计算中，无论是数值积分法[11,12]还是解析解法[13～15]，可以直接得到飞行器在地心球坐标系内的三分量：地心距r，经度L，地心纬度φ，如图2所示。因此，需要研究一种地心球坐标向大地坐标的直接转换算法，以提高计算效率。

在图2中，地心球坐标（r，L，φ）向地心直角坐标（X，Y，Z）的转换公式为

反之，地心直角坐标系向地心球坐标的转换为

考虑到空间矢量OP在XOY平面内分量和沿OZ轴分量的唯一性[16]，综合式（1）和式（7），可得几何关系表达式：

进一步，可得大地纬度和大地高程的计算公式：

式（10）可采用迭代法计算，从而得到地心球坐标向大地坐标的转换方法。迭代公式为

式（12）中，大地高程的计算由大地纬度的取值范围确定。

4 仿真分析

针对本文给出的利用空间几何关系的迭代法，将从迭代算法的有效性、迭代初值对迭代精度的影响、迭代精度随大地纬度和大地高程的变化规律等3方面进行仿真分析。

仿真分析中使用国家大地测量坐标系的CGCS2000椭球，几何参数如表1所示。

表1 CGCS2000椭球几何参数

4.1 算法有效性分析

迭代算法的有效性分析方法为：给定空间任一点的大地坐标，先转换为地心直角坐标，再利用式（8）转换为地心球坐标，用以模拟空间飞行轨迹，最后利用本文方法转换为大地坐标，并与给定的大地坐标进行比较。

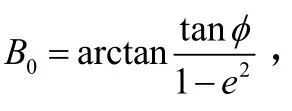
表2 有效性分析计算结果

从表2可以看出，本文给出的利用空间几何关系的迭代法计算精度明显优于直接法，与传统迭代法精度相当。但是，本文给出的迭代法不需要地心直角坐标的转换，计算效率优于传统迭代法，更适合应用于空间飞行轨迹的大地坐标计算。4.2 初值影响分析

在仿真中，L取40°，大地纬度分别取10°、4 5°、80°，大地高程取50 000 m，迭代初值分别取

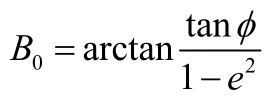
表3 初值影响分析计算结果

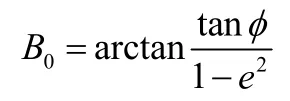
4.3 算法适用性分析

为验证利用空间几何关系的迭代法的适用性，将分析迭代精度随大地纬度和大地高程的变化规律。

在仿真中，L取40°，大地纬度为0°、-90°，每隔1°取一个点，大地高程分别取为0 km、10 km、100 km和1 000 km，以ΔB≤0.000 01＂为结束条件，大地纬度、大地高程计算误差及迭代次数分别如图3～5所示。

从图3和图4中可以看出，不同条件下，大地纬度的计算精度达到10-8″，大地高程的计算精度达到10-7m，完全满足弹道飞行器空间飞行轨迹的大地坐标精度要求。

从图5中可以看出，该迭代算法收敛速度较快，迭代次数均小于3次；迭代过程中同时利用了大地纬度和大地高程信息，因此迭代次数与纬度和高程均有关系，在低纬度和高纬度地区迭代次数较少，大地高程较高时迭代次数较多。

5 结 论

为解决弹道飞行器空间飞行轨迹的大地坐标计算问题，本文给出了一种利用空间几何关系的迭代法。通过数值计算对比分析，验证了该算法的有效性，明确了该算法的迭代初值；不同条件下的仿真结果表明，该算法具有较高的计算精度、较快的收敛速度，能够适用于弹道飞行器任意空间飞行轨迹的大地坐标计算。

本文给出的方法同样适用于近地轨道卫星、滑翔飞行器等空间飞行轨迹的大地坐标计算。

[1] 马志强, 郭福生, 陈良友, 等．靶场大地测量[M]. 北京: 国防工业出版社, 2004.

[2] 祁立学, 张萍, 杨玲. 地心直角坐标到大地坐标常用转换算法的分析与比较[J]. 战术导弹技术, 2006(2): 37-41.

[3] 崔永俊. 空间直角坐标与大地坐标之间的变换方法研究[J]. 华北工学院学报, 2003(1): 73-75.

[4] 廖鸣, 李鹏, 陈毅平, 等. 地心直角坐标和大地坐标转换算法研究[J].电子科技, 2010(2): 18-21.

[5] Bowring B R. Transformation from spatial to geographical coordinates[J]. Surveyreview, 1976(23): 323-327.

[6] Bowring B R. The accuracy of geodetic latitude and height equations[J]. Sun Rev, 1985(38): 202-206.

[7] Jones G C. New solutions for the geodetic coordinate transformation[J]. J Geod, 2002, 76(8): 437-446.

[8] Vermeille H. Direct transformation from geocentric coordinates to geodetic coordinates[J]. J Geod, 2002, 76(8): 451-454.

[9] 严伯铎. 空间直角坐标到大地坐标变换的一种非迭代法[J]. 海洋测绘, 2002(3): 9-11.

[10] 李智, 张雅声, 李延兴, 等. 空间飞行体地心坐标与大地坐标的快速精确转换[J]. 中国空间科学技术, 2004(1): 50-55.

[11] 张毅. 弹道导弹弹道学[M]. 长沙: 国防科技大学出版社, 2005.

[12] 贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科学技术大学出版社, 1993.

[13] 陈世年. 控制系统设计[M]. 北京: 宇航出版社, 1996.

[14] 李连仲. 弹道飞行器自由飞行轨道的解析算法[J]. 宇航学报, 1982, 13(1): 1-17.

[15] 郑伟, 汤国建. 弹道导弹自由段解算的等高约束解析解[J]. 宇航学报, 2007(2): 269-272.

[16] 龙乐豪, 等. 总体设计(上)[M]. 北京: 宇航出版社, 1989.

Method of Geodetic Coordinates Calculation for Flight Trajectory

Chang Xiao-hua, Feng Hai, Zhang Jie, Qiu Ya-nan
(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

Based on the spatial geometric relation-ships between geocentric spherical coordinate and geodetic coordinate, an iteration method to solve the geodetic coordinates calculation for ballistic vehicle trajectory is given. The iteration method avoids the transform of the geocentric rectangular coordinate. The efficiency of the iteration method is validated by the comparison of the traditional algorithm, and the initial iteration value is deduced. Finally, the applicability of the iteration method presented in the paper is analyzed by the numerical simulation.

Flight trajectory; Geodetic coordinates; Iteration method

TJ410

A

1004-7182(2017)03-0032-05

10.7654/j.issn.1004-7182.20170307

2015-12-10；

2016-02-25

常晓华（1982-），男，高级工程师，主要研究方向为飞行器动力学、制导与控制