20～85km高空大气密度与风场研究

黄世勇，闻 悦

（中国运载火箭技术研究院，北京，100076）

20～85km高空大气密度与风场研究

黄世勇，闻 悦

（中国运载火箭技术研究院，北京，100076）

20～85 km大气密度与风场对再入飞行器的安全及返回（即飞行器可控可达）有非常重要影响。分析了高空大气参数变化影响因素，基于CIRA-86大气模型与美国航天飞机飞行实测数据，分析了大气密度偏差范围；基于国外实测文献数据及等概率分布椭圆模型，给出了风矢量剖面，研究了风矢量剖面在飞行器设计中的应用。

大气密度；风场；风矢量剖面

0 引 言

标准大气，也称为参考大气，以平均海平面的空气温度、压力和密度为初始常数，每层大气温度作为位势高度的线性函数，采用理想气体定律与静力学方程计算得出[1]。事实上大气随时间与空间的变化极为复杂，因此实际大气参数与标准大气存在显著差异。

大气参数变化直接导致作用在飞行器上的气动力与力矩变化。对于弹道式再入飞行，再入段下降比较陡峭，所经历航程和时间较短，大气参数影响相对较小。对于升力式再入（如航天飞机），85 km以上为低热层大气，空气稀薄，密度偏差大，由于无法建立准平衡滑翔条件，飞行时间较短，横向机动距离有限，且85 km以上主要采用反作用控制系统实现稳定控制；20 km以下大气逐步过渡到平流层下部及对流层，现有无线电探空仪等多种手段可获取20 km以下大气数据。升力式再入飞行器主要在20～85 km平流层与中间层长时间飞行，航程控制能力主要在此高度区间，因此20～85 km大气密度偏差与风场对飞行安全和可控返回，即飞行器可控可达都有非常重要的影响。

1 高空大气参数变化影响因素

大气参数主要受经纬度-季节、昼夜、太阳活动及地磁因素等多种因素影响。

1.1 随经纬度-季节变化

高空大气参数随经纬度-季节变化受太阳辐射因素影响。通过观测数据发现，高空大气密度偏差最主要因素为季节与纬度，纬度越高，密度偏差越大，特别是在冬季[2]。由于地球关于极轴对称，当其它条件不变只有经度因素变化时，在构成大气的多种气体中只有部分微量元素发生了细微的改变，对气体总密度造成的影响可忽略不计[3]。从长时间尺度考虑，经度虽然对高空大气参数也有影响，但总影响甚微，可以忽略。1.2 随昼夜变化

地球自转使大气存在昼夜变化，密度和风速昼夜变化是由太阳加热的昼夜变化所引起的大气膨胀和收缩所产生的，有明显的潮汐波动特征。200 km以下大气参数受昼夜变化影响较小[4]。

1.3 随太阳活动变化

高层大气通过臭氧和电离等方式吸收太阳紫外辐射，而太阳的紫外辐射与太阳活动密切相关[4]。大气中臭氧含量很少，但在全球大气环流起着重要作用。太阳活动存在明显的近似11年、22年、5年、2年、1.7年、1.3年以及更长的周期变化，还存在27天左右短周期变化现象。

1.4 随地磁活动变化

当太阳爆发时，由太阳风带来的带电粒子撞击地球磁层发生磁暴，会有大量的能量通过焦耳加热或者高能粒子沉降等方式注入到极区的中层大气，明显改变中层大气的环流，进而改变全球大气环流状态与高空大气参数[4]，特别是在高纬度地区，地磁活动较为活跃，对大气影响较明显。

2 大气密度分析

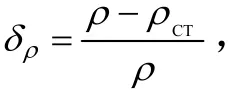
2.1 季节-纬度变化

CIRA-1986是空间研究委员会（COSPAR）国际参考大气较新版本，利用了Nimbus-5和Nimbus-6卫星多年近全球覆盖遥感数据进行修订产生，详细给出各月从地面到120 km，从80°S到80°N各等压面上大气参数分布。依据CIRA-86大气模型，采用理想气体定律（适用到86 km），可得到大气密度季节-纬度变化。

a）纬度越高，大气密度波动越明显，高度越高（50 km以上），大气密度波动越显著；

b）相同纬度及高度条件下，北半球12月、1月份和6～7月份大气密度波动明显，3～4月份和9～10月份大气密度波动相对较小，其中冬季大气密度减小，夏季大气密度增加；

c）南半球与北半球变化特性相反。

2.2 航天飞机实测数据

图1给出了美国航天飞机32次飞行的实测大气密度数据[5]，其中大气密度均值与CIRA-86季节-纬度变化长周期项基本吻合。

对应45～65 km与65～85 km高度区间，中低纬度密度偏差范围分别为-24.5%～22.7%，-39%～25.6%，高纬度大气密度偏差范围分别为-43.2%～11.2%，-57.9%～-7.8%。

3 大气风场分析

风组成可分解为平稳风、紊流、阵风[6]。平稳风，也称为定常风，指大范围内大气的均匀运动，风速及方向随时间变化平缓，与季节-纬度密切相关。紊流指围绕定常风的连续随机脉动；阵风为一种离散的或确定的风速变化，可单独使用，也可叠加到平稳风或紊流上，表示强的大气扰动。

如果观测样本数据积累足够多，则可给出较为准确风场参数，即纬向平均风、纬向速度标准差σU、经向平均风、经向速度标准差σV，及经纬向风速相关系数R(U,V)。其中经纬向风速相关系数与高度相关，在20～85 km区间内，相关系数值最大可达0.7～0.8，即经纬向风相关性比较强，但大部分情况下相关系数小于0.5，也就是经纬向风弱相关。

3.1 平稳风

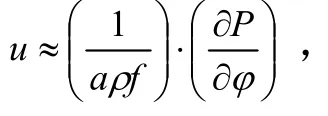
a）北半球冬季为西风，夏季为东风，冬夏季风最强，春秋为西风—东风过渡季节，春秋季节风速小于冬夏季，南半球与北半球变化特性相反；

b）最大平稳风速位于40～75 km高度，20～50°纬度区间。

径向平稳风速绝对值较小，一般小于20 m/s[8～10]。

3.2 风速标准差

3.2.1 纬向风速标准差

纬向风速标准差参考国外相关文献数据[8～10]。文献[8]以10°S、30°N、60°N作为观测点，不考虑经度因素，在不同年份、不同月份，通过百次至千余次的探空火箭及激光雷达观测，获得了10 Pa（约65 km）、100 Pa（约48 km）、1 000 Pa（约31 km）处的平稳风与纬向风速标准差。文献[9]、文献[10]给出了Ascension Island （7°S）、Wallops Island（37°N）、Churchill（59°N）、肯尼迪航天中心（KSC）（28°N）、范登堡空军基地（VAFB）（34°N）、爱德华兹空军基地（EAFB）（32°N）等6个具体地点对应的相关月份平稳风与纬向风速标准差。

平稳风与纬向风速标准差综合对比如图2至图4所示。图中各月连接折线为文献[8]中观测到的平稳风，Δ、▽、O、*等符号对应6个具体地点观测到的平稳风，其中一格表示1倍标准差：

a）文献[8]中不考虑经度因素的平稳风与3.1节理论平稳风基本上吻合；

b）具体地点平稳风与理论平稳风变化规律相同，但个别月份差别较大；

c）北半球冬季（12月、1月、2月）高空风速标准差最大；

d）北半球，除12月与1月份外，其它月份纬向风速标准差与具体地点风速标准差吻合较好。

3.2.2 经向风速标准差

经向风速标准差值随着高度的增加而增加，但小于同位置纬向风速标准差；同一高度下，纬度越高，经向风速标准差越大。20～60 km经向风速标准差小于20～30 m/s，60～85 km经向风速标准差小于40 m/s[9,10]。

3.3 风矢量剖面

风场分布为二元联合概率正态分布，其概率密度函数为

采用概率分布函数描述的),(VUP等概率分布椭圆[10,11]为

以30°N、65 km高度为例，12月份纬向平均风速为72 m/s，纬向速度标准差为29 m/s，经向平均风速为9 m/s，经向风速度标准差22 m/s，经纬向风相关系数0.53，50%、90%、95%、99%等概率风场分布如图5所示，最大风速及对应风向如表1所示。

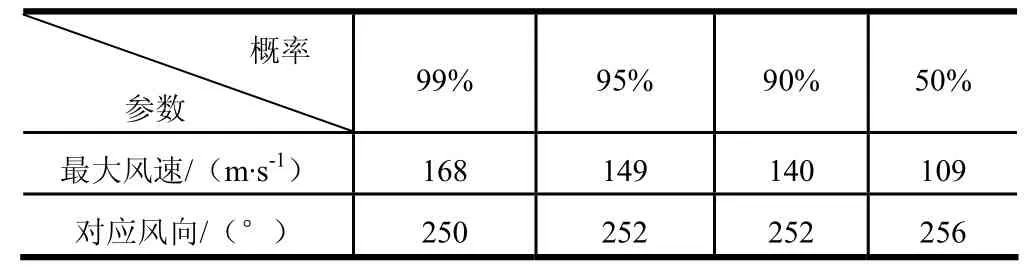
表1 不同概率情况下最大风速及对应的风向

图6a给出了12月份30°N、20～85 km高度、99%概率风矢量剖面，可见飞行器在风矢量剖面管道中飞行。图6b为不同概率下的最大风速，99%、95%、90%、50%下的最大风速分别为180 m/s、160 m/s、150 m/s、117 m/s。

分析图5及图6a，飞行器在风矢量剖面内飞行，最大风速及所对应的风向为概率边界上一点，概率边界上的风场为飞行器飞行面临的风场条件。若以最大风速、0～360°风向作为风场设计条件，则过于苛刻。对于升力式再入飞行器，一般来讲，除考虑最大风切变外，由风产生的附加侧滑对飞行器影响要比纵向产生的附加攻角更为严重，因此需在风矢量剖面基础上，基于飞行器飞行姿态，考虑与飞行器纵向对称面垂直的风场作为设计条件，如图7中VA，VB两点所示。这即可避免最大风速0～360°设计过于保守的问题，也能考虑风场影响最危险的飞行工况。

4 结 论

a）对于大气密度，纬度越高，大气密度波动越明显；高度越高，大气密度波动越显著。通过对航天飞机32次实测数据分析，45～65 km及65～85 km高度，中低纬度密度偏差范围分别为-24.5%～22.7%，-39%～25.6%，高纬度大气密度偏差范围分别为-43.2%～11.2%，-57.9%～-7.8%。

c）飞行器在概率风矢量剖面内飞行，最大风速及所对应的风向仅为风矢量剖面边界内一点，因此基于飞行器姿态，考虑与飞行器纵向垂直的风场作为设计条件，才能真实反映风场对飞行控制的影响。

[1] 季蓉芬. 全球大气扰动模型[J]. 航天返回与遥感, 1995(1): 66-81.

[2] Kent J. Utilization of global reference atmosphere modal (GRAM) for shuttle entry[R]. 87N20680, 1987.

[3] 郭正雄, 李文皓, 张珩. 地球边缘大气密度时空特性分析[J]. 宇航学报, 2012(8): 1177-1184.

[4] 都亨, 叶宗海. 低轨道航天器空间环境手册[M]. 北京: 国防工业出版社, 1996.

[5] Justus C G, Jeffries W R III, Yung S P, Johnson D L. The NASA/MSFC global reference atmospheric model_1995 Version[R]. NASA-TM-4715 96N11695, 1996.

[6] 肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993.

[7] 刘三军, 熊建刚, 万卫星等. 利用Aura卫星资料计算全球中层大气背景风场[J]. 空间科学学报, 2007, 27(5): 400-408.

[8] William R, Eric F, Marvin G. SPARC intercomparison of middle atmosphere climatologies[J]. Journal of Climate, 2014, 17(5): 986-997.

[9] Allen C E, Arthur K J. Wind distributions and interlevel correlations, surface to 60 km[R]. AFGL-ERP-713; AFGL-TR-80-0242, 1980.

[10] Johnson D L. Terrestrial environment (climatic) criteria guidelines for use in aerospace vehicle development, 2008 revision[R]. MSFC-1247; NASA/TM-2008- 215633, 2008.

[11] Smith O E, Adelfang S I. A compendium of wind statistics and models for the NASA space shuttle and other aerospace vehicle programs[R]. M-899, NAS 1.26208859, NASA CR-1998-208859, 1998.

Reasearch for Atmospheric Density and Wind Field from 20km to 85km

Huang Shi-yong, Wen Yue
(China Academy of Launch Vehicle Technology, Beijing, 100076）

The atmospheric density and wind field from 20 km to 85 km are of importance for the reentry flight and accurate return, in other words the controllability and accessibility of the vehicle. In this article, influence factors of the atmospheric parameters at high altitude are analyzed. Based on the CIRA-86 atmospheric model and NASA space shuttle flight data, the atmospheric density range is analyzed. Based on literature data and the probability ellipse model, the vector wind profile is given and its application in vehicle design is studied.

Atmospheric density; Wind field; Vector wind profile

TJ760.11

A

1004-7182(2017)03-0017-05

10.7654/j.issn.1004-7182.20170304

2016-06-24；

2016-09-01

黄世勇（1983-），男，高级工程师，主要研究方向为飞行器总体设计