欧氏距离与趋势值在中长期径流预报中的应用

邹俏俏

（辽宁省水利水电勘测设计研究院，辽宁沈阳110006）

欧氏距离与趋势值在中长期径流预报中的应用

邹俏俏

（辽宁省水利水电勘测设计研究院，辽宁沈阳110006）

中长期径流预报在水利部门的日常工作中占有重要的地位，及时、精确的预报结果可为兴利除害决策提供重要依据。清河水库通过计算欧氏距离选出与预报年份前期水文信息数值接近的年份，通过计算趋势值选出与预报年份前期水文情势变化规律相似的年份，以上两种方法选取出可以作为预报的参考年份，最终的预报结果与原预报方法的预报结果相比，精度提高较大。

欧氏距离；趋势值；中长期径流预报

中长期径流预报是水利工程设计、施工和运行管理的重要依据，在防洪、抗旱、发电、供水、航运、旅游、养殖及改善生态环境等方面能发挥显著作用。随着科学技术的提升和经济社会的发展，对水资源的管理要求更加严格，这就要求有预见期较长的中长期径流预报与精度较高的短期洪水预报相结合，为水资源的管理提供参考依据。而由于水文系统本身的复杂性，较长的预见期往往伴随着水文要素更多的变化和不确定性，从而带来误差更大的预报结果。因此，如何使预见期更长的中长期径流预报的预报结果能满足工程实际的要求成为迫切需要解决的问题。

1 基本原理

模糊数学诞生于1965年，它的创始人是美国自动控制专家查德教授。传统精确数学要求决不允许模棱两可的存在，一个对象之于一个集合，要么属于、要么不属于，两者必居其一，且仅居其一，这在某种程度上限制了数学的发展。而模糊数学可以清晰地描述某些“亦此亦彼”的过渡性状态，弥补了传统精确数学的缺憾。现在，模糊数学已应用到多个学科领域，欧氏距离和趋势值都是模糊数学中的重要概念。

1.1 欧氏距离

欧氏距离又称欧几里得度量，指在n维空间中两个点之间的真实距离，计算公式为：

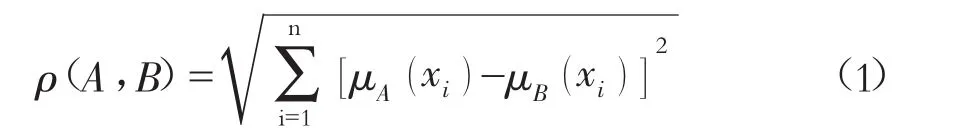
其中：ρ（A，B）为n维空间中A，B两个点之间的真实距离）为向量A在第i个维度上的坐标；）为向量B在第i个维度上的坐标。从计算公式可以看出，欧氏距离越小，则两个向量的距离越近；反之，则对应向量相差越远。

1.2 趋势值

对于论域U上有的已知标准模式Ai（i=1，2，…，m），各标准模式用n个离散点的非凸隶属函数描述，即，待识别的模式为B（b1，b2，…bj，…，bn）。

否则趋势值为：

式中：ki，j+1为趋势值；n为离散点的个数；j=1，2，…，n-1。所有趋势值相加得到的趋势累加值越大，则说明待识别模式B与标准模式Ai的发展趋势越接近，若趋势累加值为1，则待识别模式B与标准模式Ai的趋势完全一致，若趋势累加值为0，则B与Ai趋势完全不一致。趋势累加值也可简称为趋势值。

1.3 欧氏距离与趋势值在中长期径流预报中应用的可行性

根据前期水文气象资料，用成因分析和数理统计方法，对未来较长时期的水文情势进行科学的预测，称为中长期水文预报。水文预报包括径流、水位、泥沙和冰情等具体预报项目。主要针对中长期径流预报进行研究，预报对象为汛期径流总量，进行预报之前。首先是对预报因子的分析，预报因子可以从两个层面进行研究：前期水文信息的具体数值，通过比较所需预报年份与历史年份之间前期水文信息的数值，选取与所需预报年份接近的年份作为预报的参考年份；另一个层面是前期水文信息随时间的变化规律，通过比较所需预报年份与历史年份之间前期水文信息的变化规律，选取与所需预报年份变化规律相似的年份作为预报的参考年份。

计算所需预报年份预报因子与历年的预报因子之间的欧氏距离，若某年与所需预报年份间欧氏距离越小，则说明两年之间预报因子越接近，即两年之间的前期水文情势越接近，则该年的汛期径流量可以作为预报结果的参考值。

对于随时间变化的预报因子，可以计算出所需预报年份预报因子与历年预报因子之间的趋势值，若某年与所需预报年份间趋势值越接近1，则说明两年之间预报因子变化趋势越接近，即两年之间的前期水文情势变化规律越相似，则该年的汛期径流量也可以作为预报结果的参考值。

综上，欧氏距离可以计算2年间前期水文情势的接近程度，趋势值可以识别2年间前期水文情势变化规律的相似程度。通过计算所需预报年份与历年之间预报因子之间的欧氏距离和趋势值，可以选取出与所需预报年份前期水文信息数值接近且水文情势变化规律相似年份来作为预报的参考年份。

2 应用

分别将前期若干年份的汛期径流量和前期非汛期的各月径流量作为预报因子，对汛期径流量进行预报。

2.1 欧氏距离

以2014年为例，若某年与2014年预报因子之间欧氏距离越小，则该年前期水文情势与2014年越接近，该年汛期径流量与2014年接近的可能性也就越大，该年汛期径流量就可以作为预报结果的参考。

1）先讨论将前期若干年份的汛期径流量作为预报因子的情况。取6年为例，即将2008年至2013年各年的汛期径流量作为2014年汛期径流量的预报因子，计算2014年与历年预报因子之间的欧氏距离，计算结果：为历年与2014年预报因子之间欧氏距离最小的3个年份为1968年，1979年和2009年。

2）再讨论将前期非汛期的各月径流量作为预报因子的情况。清河水库汛期为每年6月至9月，非汛期为10月至次年5月，则将2013年10月至2014年5月各月的径流量作为2014年汛期径流量的预报因子，计算不同年份预报因子之间的欧氏距离，计算结果：历年与2014年预报因子之间欧氏距离最小的3个年份为1965年，2004年和2011年。

2.2 趋势值

以2014年为例，若某年与2014年预报因子之间趋势值越大（因为趋势值在0到1之间，即趋势值越接近1），则该年前期水文情势变化规律与2014年越接近，该年汛期径流量与2014年接近的可能性也就越大，该年汛期径流量就可以作为预报结果的参考。

1）先讨论将前期6年的汛期径流量作为预报因子的情况。计算2014年与历年预报因子之间的趋势值。计算结果：历年与2014年预报因子之间趋势值较大的年份有1968，1970，1973，1975，1977，1979，1984，1987，1992，1995，2002，2005，2009年。

再讨论将前期非汛期的各月径流量作为预报因子的情况。计算2014年与历年预报因子之间的趋势值。计算结果：历年与2014年预报因子之间趋势值较大的年份有1962，1963，1964，1964，1975，1978，1984，1987，1988和2004。

2.3 预报

综上，每种方法选取出的年份与2014年的汛期前期水文情势或前期水文情势变化规律均有一定的相似性，可以取选定年份的汛期径流量的平均值作为预报结果。采用相同方法对2012年和2013年汛期径流量进行预测，4种方法的预报结果见表1。

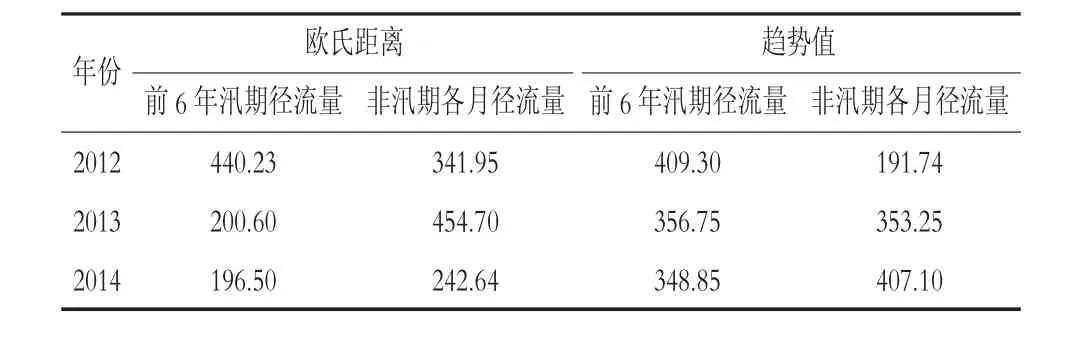
表1 2012—2014年汛期径流量预报结果106m3

2.4 预报结果分析

清河水库原中长期径流预报采用周期叠加法、平稳时间序列法、周期叠加与平稳时间序列结合法、历史演变法4种方法进行预报，并综合4种方法的预报值得出最终的预报结果。但清河水库年际汛期径流量变化较大，在水库建成后汛期径流量最大年份（1964年，1082.9×106m3）甚至达到汛期径流量最小年份（2000年，35.6×106m3）汛期径流量的30倍以上。因此，预报结果往往与实际值相差较大。多年预报结果的误差值甚至达到了130.3%。2012年至2014年汛期实际径流量分别为319.8×106m3，590.7×106m3，217.6×106m3，经计算，所采用方法的预报结果误差值统计见表2。

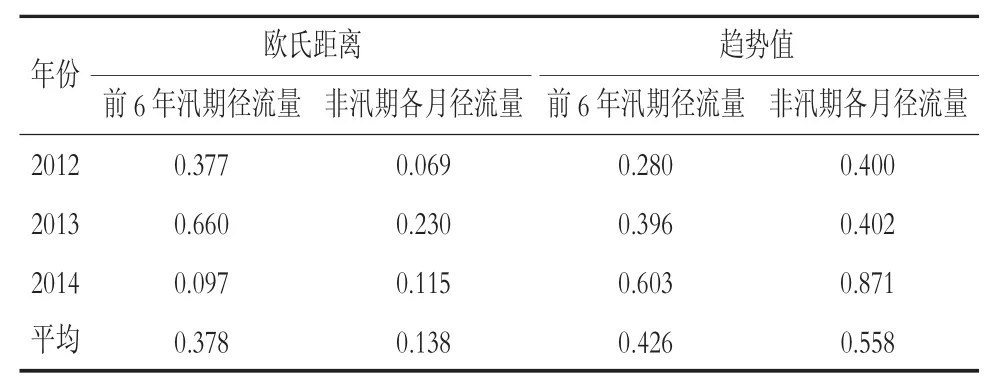
表2 2012—2014年预报结果误差统计

不难看出，清河水库采用的4种方法的预报结果的误差值均小于原预报方法高达130.3%的误差值。其中以非汛期各月径流量为预报因子，通过计算欧氏距离选取参考年份进行预报的方法最终得到的预报结果与汛期实际径流量最为接近，平均误差值仅为13.8%，该方法的预报结果能够为水利部门提供更有力的决策依据，其他3种方法所得的预报值也能为水利部门确定最终预报结果提供参考依据。

3 结论

将欧氏距离和趋势值应用到中长期径流预报中，利用欧氏距离选取出与所需预报年份前期水文信息数值接近的年份，利用趋势值选取出与所需预报年份水文情势变化规律相似的年份。将以上两种方法选出的年份作为参考，对汛期径流量进行预报。最终的预报结果与原预报方法的预报结果相比精度提高较大，能更好地满足相关水利部门的工作要求。

［1］詹道江，叶守泽.工程水文学（第三版）［M］.北京：中国水利水电出版社，2000.

［2］汤成友，官学文，张世明.现代中长期水文预报方法及其应用［M］.北京：中国水利水电出版社，2008.

［3］鲁帆，严登华，王勇，蒋云钟.中长期径流预报技术与方法［M］.中国水利水电出版社，2012.

［4］王本德.水文中长期预报模糊数学方法［M］.大连：大连理工大学出版社，1993.

［5］彭勇.中长期水文预报与水库群优化调度方法及其系统集成研究［D］.大连理工大学，2007.

［6］李敏.基于可变模糊集理论的径流预报方法研究［D］.大连理工大学，2008.

［7］吴佳文.水文时间序列数据挖掘算法研究与应用［D］.沈阳农业大学，2011.

［8］刘瑞元.加权欧氏距离及其应用［J］.数理统计与管理，2002，21（5）：17-19.

［9］李敏.可变模糊近似推理方法在径流中长期预报中的应用［J］.水电能源科学，2010，28（2）：16-18.

P333

A

1002－0624（2017）06－0034－03

2016-09-20