社会群体性事件的协同演化博弈研究
2017-06-21王循庆孙晓羽
王循庆,孙晓羽
(山东工商学院 公共管理学院,山东 烟台 264005)
社会政策与治理研究
社会群体性事件的协同演化博弈研究
王循庆,孙晓羽
(山东工商学院 公共管理学院,山东 烟台 264005)
社会群体性事件的频发已经成为威胁公共安全的重要隐患。针对不同社会网络结构下群体性事件的演化问题,运用复杂网络和演化博弈理论,构建了群体性事件个体策略与网络结构协同演化博弈模型。研究表明:在社会网络中个体说服其相邻个体采取抗争策略获得额外收益大于其说服成本,且其邻居接受说服获得收益大于不接受说服获得收益的条件下,随着WS小世界网络重连概率增大,即网络异质性越大,其演化至均衡策略时间越短;异质网络中节点度大的个体,具有较大影响力,更容易说服带动周围个体接受其策略,结成联盟采取抗争策略,形成羊群效应。高度异构的BA无标度网络策略的演化时间明显小于WS小世界网络的演化,BA无标度网络较WS小世界网络更容易引发群体性事件。
群体性事件;协同演化博弈;复杂网络;演化稳定策略;稳定性
一、引言
当前随着我国经济的快速发展,利益格局与社会控制模式正在发生巨大的改变。由于我国正处于经济转轨与社会转型的关键时期,社会利益结构的分化速度加快,不同社会群体的利益博弈关系趋于复杂,导致不同利益群体之间的矛盾和冲突正在日渐增多。例如2005年安徽池州事件、2008年贵州翁安事件、2011年潮州古巷事件、2014年云南晋宁征地惨案等,这些事件的频繁发生反映了我国社会建设过程中制度的不完善和公共管理的缺位与不足。群体性事件不仅会对社会群体的心理造成不安影响,而且会对社会公众的财产和生命安全构成威胁,导致政府公信力下降[1]。
群体性事件具有结构复杂性、信息匮乏性、矛盾对抗性、难以预测性等高度复杂性的非常规突发事件特征[2],目前研究多基于博弈理论分析和探讨群体性事件中群体策略博弈过程,徐寅峰、刘德海[3]基于主观博弈模型对群体性事件的产生根源进行了分析,并对产生根源的相关影响因素进行了探讨。Lo等[4]将参与博弈的个体行为选择过程中各种备选的行为看作是策略集,建立了群体行为选择的非合作博弈模型,并采用混合策略下的纳什均衡对社会群体行为的涌现机理进行了详细解释分析。Liu和Wang[5]建立了政府机构与社会群体的博弈模型,对政府的不同应急处置策略进行了探讨,并分析了模型的Nash均衡。王循庆等[6]对比分析了引入上级政府惩罚和未引入上级政府两种不同情景下的群体性事件演化博弈问题。郑君君等[7]考虑当群体间存在信息交互时,运用演化博弈和优化理论分析政府部门采用舆情引导下的环境群体性事件演化特征。晏永刚等[8]针对污染型邻避设施规划建设引发的群体性事件,采用演化博弈构建了公众与投资企业的演化博弈模型,并分析了公众与投资公司的演化稳定性。
上述研究主要是在均质社会网络结构下分析群体性事件的演化问题,而真实的社会网络结构多表现为小世界网络、无标度网络等复杂网络特性[9]。社会网络的拓扑结构对个体的行为策略产生显著影响,因此针对社会群体网络结构进行演化分析已经成为当前研究重点[10]。Human和Provan[11]分析了社会网络的演化过程,并探讨了网络节点间的交互对社会网络拓扑结构的作用机制。Lieberman等[12]采用数值模拟囚徒困境在小世界网络、无标度网络上的演化过程,研究了网络上的合作行为规律。Eguíluz等[13]通过大量的计算机模拟,探讨了网络中不同角色的个体在网络中所起到的作用,节点度大且处于领导地位的节点能够对维持网络的合作稳定起到重要的作用,但随着网络的演化其领导作用也会随之发生改变。Fu等[14]基于实证方法分析了社交熟人间的网络特性,研究表明现实中的社交网络具有小世界和无标度特性,并且发现与网络中节点度大的点连接能够提高合作水平,保持合作的稳定性。Burt[15]对网络中相邻两个个体的信息交流进行了探讨,发现处于信息优势地位的个体对信息交流具有控制地位,表明信息优势对网络个体之间交流的重要性。
尽管一些文献对个体行为与社会网络结构演化做了相关研究[16,17],但针对群体性事件演化中的个体策略与群体网络结构协同演化涉及较少。另外,现有研究缺乏进一步研究网络的异质性对均衡策略演化的影响。因此,本文基于复杂网络和演化博弈理论构建了群体性事件个体策略与网络结构协同演化博弈模型,对比分析WS小世界网络和BA无标度网络两种不同社会群体网络的拓扑结构对个体策略选择与行为模式的影响,为政府部门科学应对社会群体性事件提供决策支撑。
二、问题描述与模型建立
社会群体性事件的发生通常涉及多方主体,在以城市拆迁、征地补偿、环境污染等引发的群体性事件中,以拆迁房屋居民、失地农民、普通民众等利益相关者为代表的弱势群体成为事件的重要参与者。在事件发生过程中,社会群体的个体之间存在着信息交互,他们彼此之间的观点会相互影响[7]。通过群体网络中个体间的信息传播和相互影响,以及个体间的利益博弈,都会影响个体的策略选择。由于实际中社会群体的个体是具有有限理性的,在博弈过程中会相互学习、相互模仿,追求自身利益最大化。因此本研究将结合群体中个体间的博弈特征,分析个体策略与社会网络结构间的动态演化过程。
(一)模型假设及收益矩阵
考虑一个社会弱势群体,将弱势群体社会网络中人群分为两类:个体A类与个体B类。这两类个体随机的进行配对,个体A与其随机邻居个体B进行交互博弈。其中在与强势群体争夺某种社会资源时,假如个体A有抗争意向,对其邻居个体B可以采取说服(用L表示)或者不说服(用N表示)两种策略,则个体A的策略集合为STA={L,N};而个体B可以选择的策略是接受(用K表示)或者不接受(用X表示)两种策略,因此个体B的策略集合为STB={K,X}。在个体间博弈过程中,假设个体A采取不说服策略N的比例为p,则采取说服策略L的比例为1-p,p∈[0,1];邻居个体B采取不接受策略X的比例为q,采取接受策略K的比例为1-q,q∈[0,1]。
针对上述博弈策略,在进行策略博弈过程中的每一次,个体A与其邻居个体B的博弈收益都由这两个个体所选择的策略共同决定:
(1)当个体A对其邻居个体B采取说服策略时,若个体B接受个体A的说服并采取与个体A同样的策略时,个体A除了其自身的固定收益Q,还会获得说服其邻居个体B成功后的额外收益Δq,同时个体A会付出此次博弈过程中说服的成本C,个体B的收益为HK;若个体B不接受个体A的说服,并且采取了与个体A相反的策略,个体A的收益由其自身的固定收益Q与说服的成本C构成,个体B会获得采取与个体A相反的策略收益HX。
(2)当个体A对其邻居个体B采取不说服策略时,若个体B盲目接受并采取与个体A同样的策略,会由于其盲目性可能造成被欺骗,给个体B带来一定的损失φ,则个体B的收益为HK-φ,个体A获得的收益为Q;若个体B理性的不接受,采取了与个体A相反的策略,个体B会获得收益HX,个体A的收益为Q。
根据以上分析,可以得到个体A与个体B博弈收益矩阵,如表1所示。
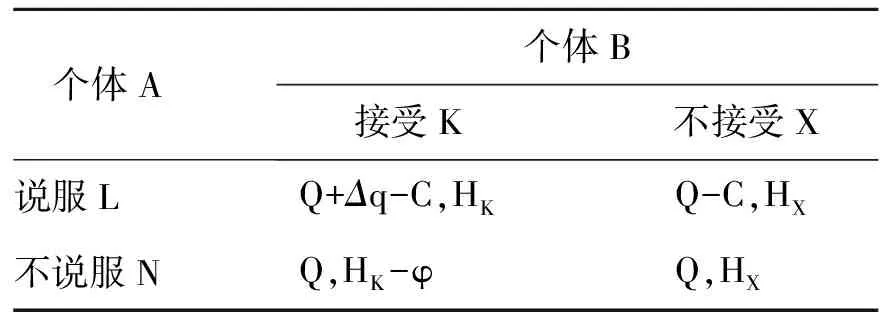
表1 个体间博弈收益矩阵
(二)模型建立
1.个体A的复制动态方程与均衡分析
个体A采取说服策略L和不说服策略N的期望收益分别为:
ΠL=(Q+Δq-C)(1-q)+(Q-C)q,
(1)
ΠN=Q(1-q)+Qq.
(2)
则个体A的平均收益为:
ΠA=ΠL(1-p)+ΠNp.
(3)
个体A的演化博弈复制动态方程为:
p(1-p)[(C-Δq)+Δq·q].
(4)
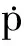
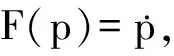
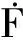
(5)
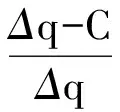
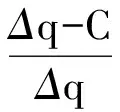
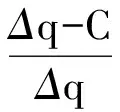
由以上分析,可以得到个体A的演化博弈复制动态演化趋势,如图1所示。
2.个体B的复制动态方程与均衡分析
个体B采取接受策略K和不接受策略X的期望收益分别为:
ΠK=HK(1-p)+(HK-φ)p,
(6)
ΠX=HX(1-p)+HXp .
(7)
则个体B的平均收益为:
ΠB=ΠK(1-q)+ΠXq .
(8)
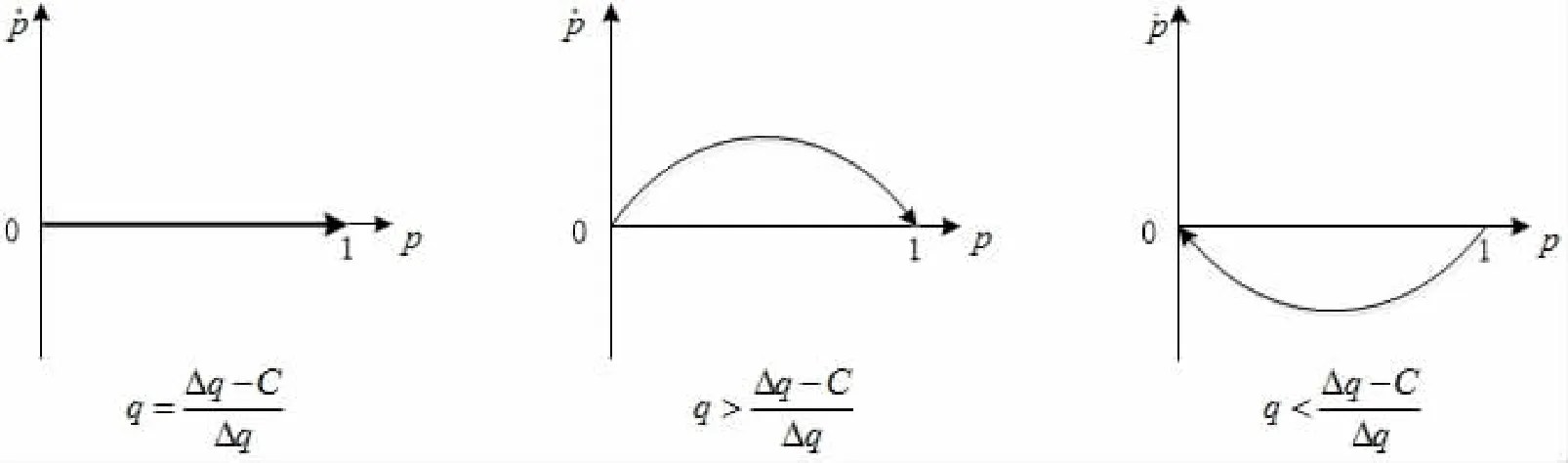
图1 个体A演化博弈复制动态相位图
个体B的演化博弈复制动态方程为:
q(1-q)[(HX-HK)+φp] .
(9)
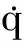

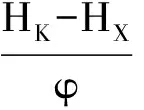
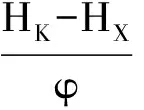
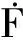
(10)
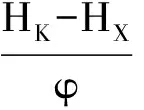
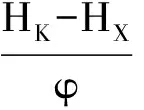
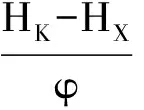
由以上分析,可以得到个体B演化博弈复制动态演化趋势,如图2所示。
(三)混合策略稳定性分析
由式(4)和(9)可以得到一个由个体A与其随机邻居个体B构成的二维动力系统为:
依据Friedman[18]提出的方法,其二维动力系统平衡点的稳定性是由这两个个体所组成的二维动力系统的雅克比矩阵局部稳定性分析得到,该系统的雅克比矩阵为:
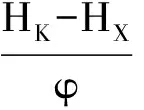
提出命题:当Δq-C>0且HK-HX>0时,系统存在唯一的演化稳定策略ESS为(0,0)。
证明:
首先计算出各点处的行列式和迹,如表2所示。
针对表2,当满足条件(I)Δq-C>0且HK-HX>0时,对均衡点进行稳定性分析,结果如表3所示。
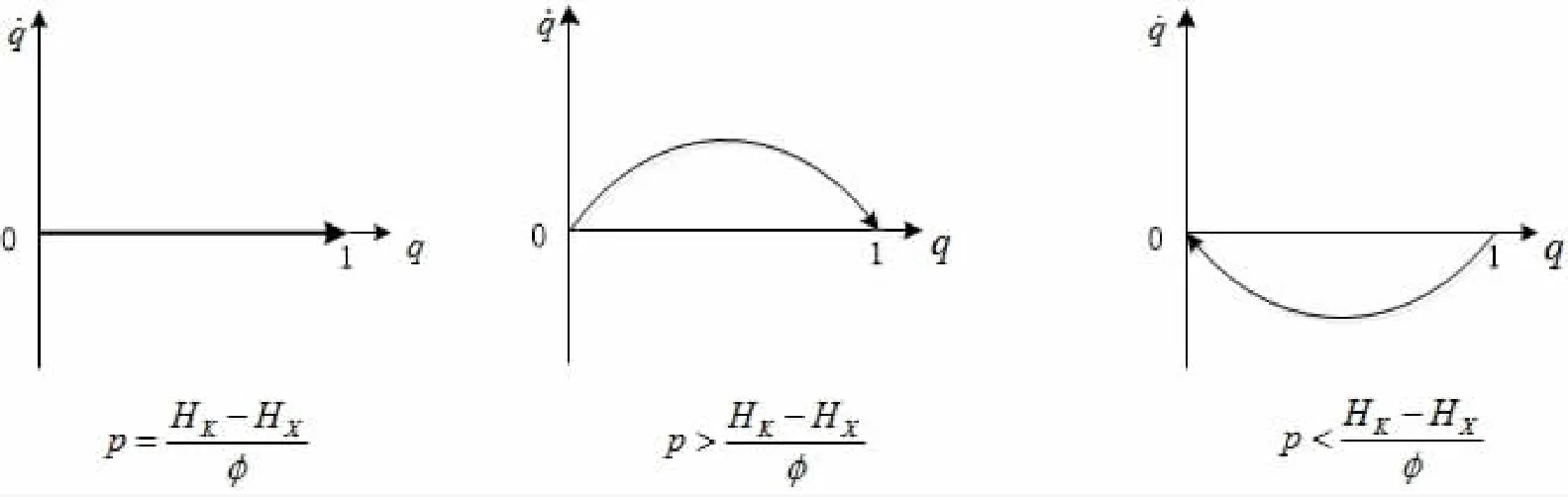
图2 个体B演化博弈复制动态相位图
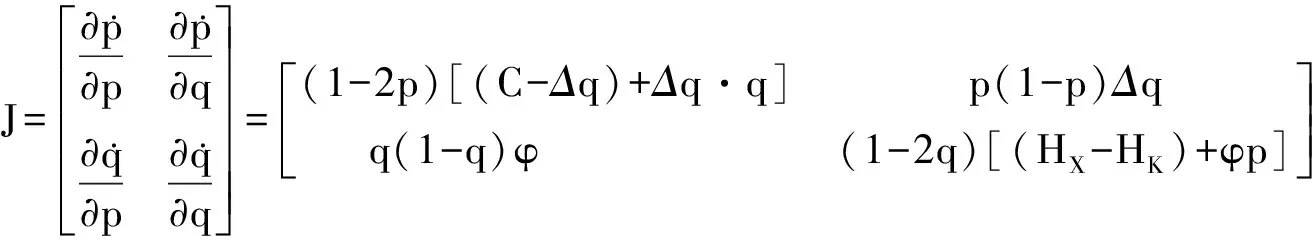
(12)

表2 系统平衡点及其行列式和迹
从表3可以看出,当Δq-C>0且HK-HX>0,即Δq>C且HK>HX时,系统存在唯一演化稳定点(0,0)和一个不稳定点(0,1)以及两个鞍点(1,0)、(1,1)。即表示系统不管处于任何初始状态,最终都会演化至稳定点(0,0),其表示个体A与其邻居个体B这两个个体最终的演化均衡策略是(0,0)。根据假设,Δq>C表示个体A说服个体B采取同样策略获得的额外收益大于其说服成本,HK>HX则表示个体B接受个体A说服获得的收益大于不接受说服获得的收益时,两个个体将会选择均衡策略(说服,接受)。其演化相图如图3所示。
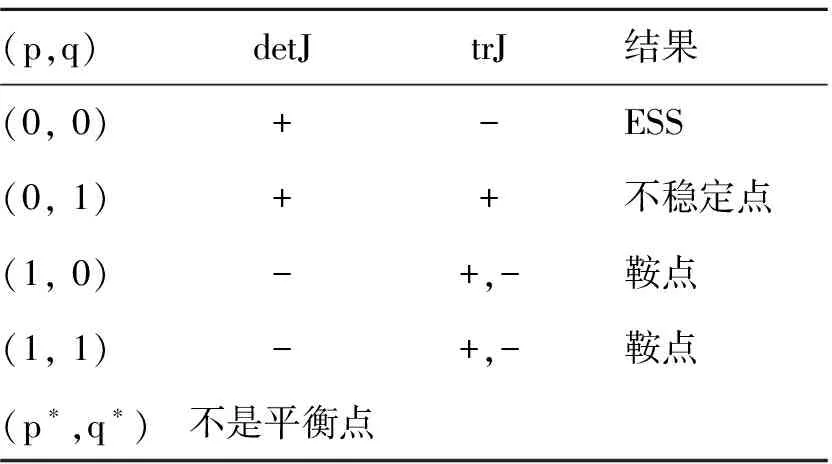
表3 条件(I)时系统平衡点及局部稳定性
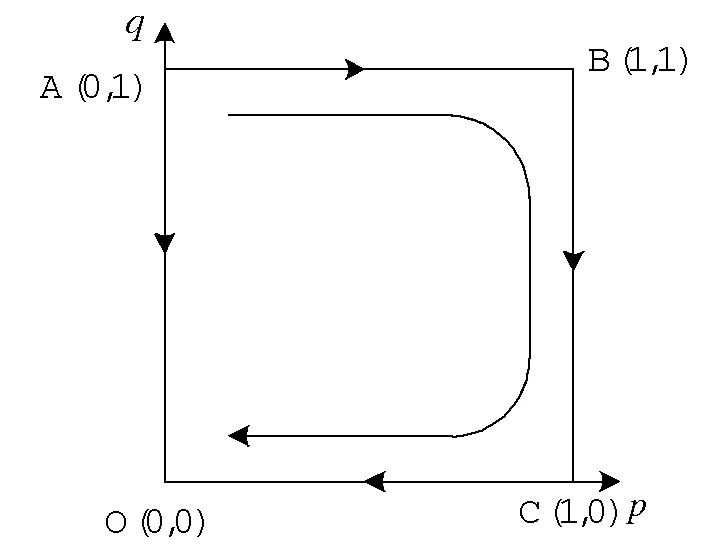
图3 条件(I)时系统演化动态相图
(四)复杂群体网络上个体博弈策略
网络的拓扑结构和网络中博弈个体的策略选择是博弈演化的两个重要影响因素。本节建立了WS小世界网络和BA无标度网络上个体演化博弈策略,为分析不同社会网络拓扑结构下的群体性事件演化提供理论支撑。
初始化时,首先将WS小世界网络中的所有节点分为个体A和个体B两类,其中个体A在整个网络中的节点比例为α,则个体B占的比例即为1-α。在初始状态个体A随机选择说服策略L或者不说服策略N,而个体B在初始状态随机的选择接受策略K或者不接受策略X。然后,在每一轮博弈中,网络中的节点都与它相连的所有邻居分别进行一次博弈。在每一轮博弈结束后,个体A或个体B都将更新其自身的策略,更新策略遵循的规则如下:
个体A在与其相连接的KA个邻居中随机地选择个体B,依据公式(1)、(2)计算个体A选择说服策略L或者不说服策略N所得到的收益分别为ΠL和ΠN;依据公式(6)、(7)计算个体B选择接受策略K或者不接受策略X所得到的收益分别为ΠK和ΠX。个体A或个体B下一轮博弈更换策略的概率分别为
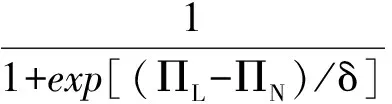
(13)
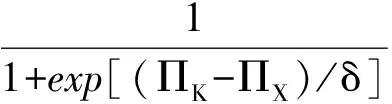
(14)
其中,参数δ为噪声系数。若δ→∞时,个体A和个体B将在下一轮博弈中进行完全的随机更新;若δ→0时,个体A和个体B将采取确定的模仿规则;通常取参数δ=0.1。BA无标度网络上个体博弈演化策略同上。
三、情景仿真分析
假设一个弱势群体社区网络总人数N=1 000,参数取值分别为:Q=20,Δq=8,C=4,HK=16,HX=10,φ=7。个体A与个体B在整个网络总人数中比例各占50%。基于WS小世界网络和BA无标度网络两种不同类型的复杂社会网络进行演化博弈情景仿真模拟,观察随着时间T的变化对不同社会群体网络结构下个体策略演化的影响。
(一)情景1——WS小世界网络上的演化博弈
这里对WS小世界网络节点总数取N=1 000,平均节点度
(1)从图4和图5可以发现,当满足命题1条件Δq-C>0且HK-HX>0,即Δq>C且HK>HX时,社会网络中个体A说服其邻居个体B采取抗争策略获得额外收益大于其说服成本,且其邻居个体B接受说服获得收益大于不接受说服获得的收益条件时,所有A类个体与B类个体最终演化至采取(说服,接受)策略。此时,WS小世界网络中所有个体观点都达成一致,即形成统一抗争意向,导致出现了羊群效应。
(2)从图4可以看出,WS小世界网络重连概率pWC取值pWC=0.2,pWC=0.4,pWC=0.6,pWC=0.8时,A类个体演化至均衡策略时间分别是T=255,T=234,T=208,T=148。此时网络的平均路径长度分别为L=6.795 5,L=5.864 0,L=5.468 2,L=5.354 8,网络的聚类系数为C=0.259 1,C=0.123 5,C=0.031 9,C=0.007 9。这表明随着网络重连概率pWC增大,平均路径长度减小,聚类系数减小,网络中A类个体演化至均衡策略时间也明显减小。
从图5可以看出,重连概率pWC取值pWC=0.2,pWC=0.4,pWC=0.6,pWC=0.8时,B类个体演化至均衡策略时间分别是T=229,T=199,T=164,T=128。这表明随着网络重连概率pWC增大,B类个体演化至均衡策略时间显著减小。
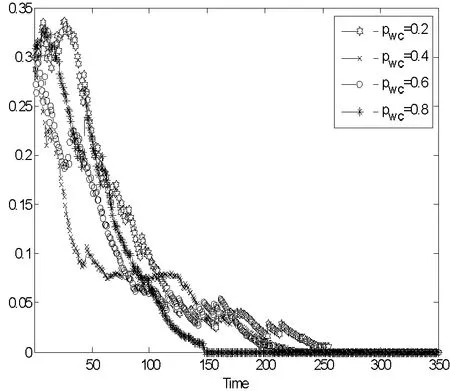
图4 重连概率pWC=0.2,0.4,0.6,0.8不同取值下A类个体策略演化过程
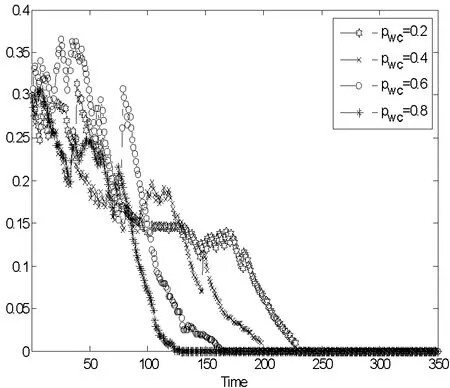
图5 重连概率pWC=0.2,0.4,0.6,0.8不同取值下B类个体策略演化过程
(3)综上可以发现,随着网络重连概率增大,演化至均衡策略时间明显减小。这是由于随着网络重连概率增大,网络变得更加异质,而异质网络中节点度大的个体,具有较大影响力,更容易说服带动邻居个体接受其策略,易结成联盟采取抗争策略,因此更容易形成羊群效应,导致所有个体演化至均衡策略的时间显著减小。
(二)情景2——BA无标度网络上的演化博弈
这里对BA无标度网络节点总数取N=1 000,网络初始节点数m0和新节点连接边数m(其中m0=m)分别取值:m0=m=2,m0=m=3,m0=m=4,m0=m=5。初始状态A类个体与B类个体选择不说服或不接受策略的比例分别为:p0=0.3,q0=0.3。图6和图7分别给出了BA无标度网络上A类个体与B类个体博弈策略的演化过程,演化策略中噪音参数δ=0.1,图中横坐标Time表示时间段,纵坐标表示选择不说服或不接受策略的比例。
(1)与同样网络规模N=1 000,平均节点度
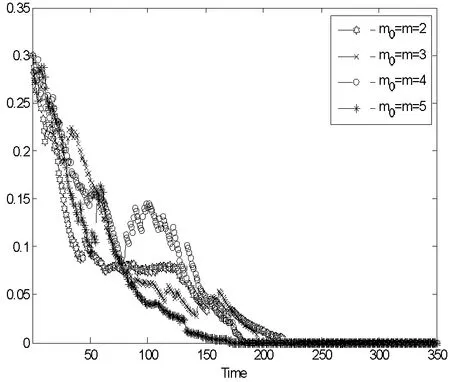
图6 m0=m=2,3,4,5不同取值下A类个体策策略演化过程
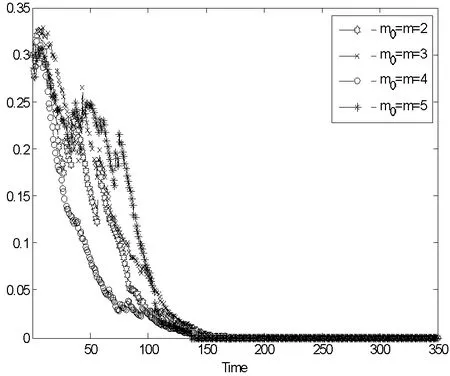
图7 m0=m=2,3,4,5不同取值下B类个体策略演化过程
(2)从图6可以看出,BA无标度网络初始节点数m0和新节点连接边数m取值m0=m=2,m0=m=3,m0=m=4,m0=m=5时,A类个体演化至稳定策略的时间分别是T=173,T=185,T=196,T=218。此时网络的聚类系数分别是C=0.023 2,C=0.029 5,C=0.031 5,C=0.033 6。这表明随着网络初始节点数m0和新节点连接边数m增大,网络聚类系数增大,网络中A类个体演化至均衡策略的时间也明显增大。从图7可以看出,网络初始节点数m0和新节点连接边数m取值m0=m=2,m0=m=3,m0=m=4,m0=m=5时,B类个体演化至稳定策略的时间分别是T=137,T=141,T=155,T=169。这表明随着网络初始节点数m0和新节点连接边数m增大,B类个体演化至均衡策略的时间也显著增加。
(3)综上可以发现,随着BA无标度网络初始节点数m0和新节点连接边数m增大,网络聚类系数增大,演化至均衡策略的时间也显著增长。这是由于聚类系数增大改变了BA无标度网络的拓扑结构,聚类系数增大实际上增加了网络中三角形结构数量,三角形结构对应于现实网络中彼此非常熟悉完全透明的一种社会关系。聚类系数越大,网络中个体间信息透明度越高,个体被说服欺骗的可能性就越低,其最终演化至均衡策略的时间就会越大。
四、结语
本文研究了不同社会网络结构下群体性事件的演化问题,基于复杂网络和演化博弈理论构建了群体性事件个体策略与网络结构协同演化博弈模型,分析了WS小世界网络和BA无标度网络两种不同社会群体网络的拓扑结构对个体策略选择与行为模式的影响,并在此基础上进行了情景仿真模拟,研究发现:在网络中个体说服其相邻个体采取抗争策略获得的额外收益大于其说服成本,且其邻居接受说服获得的收益大于不接受说服获得收益的条件下,随着WS小世界网络重连概率增大,即网络异质性越大,其演化至均衡策略时间越短;异质网络中节点度大的个体,具有较大影响力,更容易说服带动周围个体接受其策略,结成联盟采取抗争策略,形成羊群效应;高度异构的BA无标度网络策略的演化时间明显小于WS小世界网络的演化,BA无标度网络较WS小世界网络更容易引发群体性事件。基于上述分析,提出几点建议。
第一,为了控制暴力事件的发生,在对采取暴力抗争行为加大惩罚力度的同时,还应该从根本上解决弱势群体的利益诉求。在弱势群体社会网络中个体之间应该加强信息的交流沟通,增强信息公开透明化。同时,政府部门应加强舆情引导,提高公信力,切实回应和及时解决民众的利益诉求问题。
第二,群体网络中处于领导地位拥有众多关系圈的个体对其他个体有较大的影响力,他们的行动策略也是其他个体的主要参考依据。所以,针对具有领导地位的个体应加强劝阻疏导,尽量避免其采取暴力抗争策略,正确引导群体网络中其他个体采取正确合理的方式表达诉求,及时解决群体间的内部矛盾。另外,在提高群体参与积极性基础上,进一步完善参与制度,引导公众通过新媒体平台、社交平台、网络平台等多种途径表达诉求。
第三,社会群体网络拓扑结构的不同会对群体性事件的演化产生直接影响,所以应在现实中针对不同的社会群体网络结构制定不同的应对措施。结合社会网络的不同拓扑结构,尤其像BA无标度网络等特性的社会网络,例如具有无标度网络特性的农村人际网络、欠薪民工人际网络等,应重点对其进行预防控制,及时发现群体网络中的利益诉求,保持与其沟通协调,化解社会群体的矛盾,避免群体采取过激行为。
本文建立的社会群体性事件个体策略与网络结构协同演化博弈模型,适用于因征地补偿、城市拆迁、环境污染等引起的社会群体性事件的分析和研究。本研究对探讨群体性事件中个体策略与网络结构的协同演化过程,并为科学预防和控制群体性事件提供决策支持。然而,本模型仍存在一些不足,如模型中没有考虑社会网络的动态变化,接下来将进一步探讨分析社会网络拓扑结构随时间变化对个体策略行为的影响问题。
[1]Kersten A, Sidky M. Re-aligning rationality: Crisis management and prisoner abuses in Iraq [J]. Public Relations Review,2005,31(4):471-478.
[2]刘德海.群体性事件中政府机会主义行为的演化博弈分析[J].中国管理科学,2010,18(1):175-183.
[3]徐寅峰,刘德海.群体性事件产生根源的主观博弈分析[J].预测,2004,(6):43-46.
[4]Lo S M, Huang H C, Wang P,et al. A game theory based exit selection model for evacuation [J]. Fire Safety Journal,2006,41(5):364-369.
[5]Liu D, Wang W. How to analyze a type of game problem between dissymmetrical players? [C].重庆: 7th World Congress on Intelligent Control and Automation, 2008:6192-6196.
[6]王循庆,李勇建,孙华丽.基于情景推演的群体性突发事件演化博弈分析[J].管理科学,2015, (6):133-143.
[7]郑君君,闫龙,张好雨,等.基于演化博弈和优化理论的环境污染群体性事件处置机制[J].中国管理科学, 2015,23(8):168-176.
[8]晏永刚,姚秋霞,刘蓉,等.污染型邻避设施规划中公众参与行为的演化博弈分析[J].城市发展研究,2017,24(2):91-97.
[9]Hauert C, De Monte S, Hofbauer J, et al. Volunteering as red queen mechanism for cooperation in public goods games [J]. Science,2002,296(5570):1129-1132.
[10]Ohtsuki H, Hauert C, Lieberman E, et al. A simple rule for the evolution of cooperation on graphs and social networks [J]. Nature,2006,441(7092):502-505.
[11]Human S E, Provan K G. Legitimacy building in the evolution of small-firm multilateral networks: A comparative study of success and demise [J]. Administrative Science Quarterly,2000,45(2):327-365.
[12]Lieberman E, Hauert C, Nowak M A. Evolutionary dynamics on graphs [J]. Nature,2005,433(7023):312-316.
[13]Eguíluz V M, Zimmermann M G, Cela-Conde C J, et al. Cooperation and the emergence of role differentiation in the dynamics of social networks [J]. American Journal of sociology,2005, 110(4):977-1008.
[14]Fu F, Chen X, Liu L, et al. Social dilemmas in an online social network: the structure and evolution of cooperation [J]. Physics Letters A,2007,371(1):58-64.
[15]Burt R S. Structural holes: The social structure of competition [M].Boston:Harvard university press,2009.
[16]Santos F C, et al. Evolutionary dynamics of social dilemmas in structured heterogeneous populations [J]. Proceedings of the National Academy of Sciences of the United States of America,2006,103(9):3490-3494.
[17]Hanaki N, Peterhansl A, Dodds P S, et al. Cooperation in evolving social networks [J]. Management Science,2007,53(7):1036-1050.
[18]Friedman D. Evolutionary games in economics [J]. Journal of the Econometric Society,1991,(59):637-666.
[责任编辑:陈宇涵]
10.3969/j.issn.1672-5956.2017.03.015
2017-03-17
国家自然科学基金项目“非常规突发情境下危险化学品灾害事故的情景构建与动态推演研究”(71603109);山东省自然科学基金“基于情景构建与动态推演的重大危险化学品灾害事故演化机理及应急决策研究”(ZR2016GB04)
王循庆,1985生,男,山东潍坊人,山东工商学院讲师,博士,研究方向为公共危机管理,(电话)0535-6904949。
D
A
1672-5956(2017)03-0109-09
