Prediction of Blood-to-Brain Barrier Partitioning of Drugs and Organic Compounds Using a QSPR Approach

GOLMOHAMMADI Hassan DASHTBOZORGI Zahra KHOOSHECHIN Sajad

(1Young Researchers and Elite Club, Yadegar-e-Imam Khomeini (RAH) Shahr-e-Rey Branch, Islamic Azad University, Tehran, Iran;2Young Researchers and Elite Club, Central Tehran Branch, Islamic Azad University, Tehran, Iran)

Prediction of Blood-to-Brain Barrier Partitioning of Drugs and Organic Compounds Using a QSPR Approach

GOLMOHAMMADI Hassan1,＊DASHTBOZORGI Zahra2KHOOSHECHIN Sajad2

(1Young Researchers and Elite Club, Yadegar-e-Imam Khomeini (RAH) Shahr-e-Rey Branch, Islamic Azad University, Tehran, Iran;2Young Researchers and Elite Club, Central Tehran Branch, Islamic Azad University, Tehran, Iran)

The purpose of this study was to develop a quantitative structure-property relationship (QSPR) model based on the enhanced replacement method (ERM) and support vector machine (SVM) to predict the blood-to-brain barrier partitioning behavior (logBB) of various drugs and organic compounds. Different molecular descriptors were calculated using a dragon package to represent the molecular structures of the compounds studied. The enhanced replacement method (ERM) was used to select the variables and construct the SVM model. The correlation coefficient, R2, between experimental results and predicted logBB was 0.878 and 0.986, respectively. The results obtained demonstrated that, for all compounds, the logBB values estimated by SVM agreed with the experimental data, demonstrating that SVM is an effective method for model development, and can be used as a powerful chemometric tool in QSPR studies.

Quantitative structure-activity relationship; Blood-to-brain barrier partitioning; Drug; Enhanced replacement method; Support vector machine

1 Introduction

The blood-brain (BB) distribution of a molecule is an important feature to assess the suitability of a molecule as a drug for the central nervous system (CNS)1-5. The blood-brain barrier (BBB) separates the brain from the blood stream and limits the transport of many substances from the systemic circulation into the brain tissue. In experiments, the relatively affinity for the blood or brain tissue can be expressed in terms of the logarithm of the blood to-brain partition coefficient, logBB (Eq.(1)).

where Cbrainand Cbloodare the equilibrium concentrations of the drug in the brain and the blood, respectively.

In vitro experimental determination of the blood-brain permeation is often complex and depends heavily on the compound's stability, purity, assay condition, etc. while in vivo determinations are complicated by the need for radio-labeled compound in some cases6-9.

Although the laborious experimental measurement of the blood-brain distribution of a compound as described by equation (1) is the ideal approach, the experiments are a major bottleneck for high-throughput screening of large molecular libraries. Therefore, rapid and accurate computational methods for screening large chemical databases or virtual libraries are desirable to assist the experimental drug discovery process. Quantitative structure-property relationships (QSPR) studies have been established to be a proficient computational tool in understanding the correlation between the structure of molecules and their activities. QSPR is a mathematical method that relates the proprties of interested molecule to its structural features.

Various techniques have been employed for the QSPR modeling of logBB, e.g., multiple linear regression (MLR)10, partial least squares (PLS)11-13, and artificial neural networks (ANNs)14,15. However, linear methods are much limited for a complex biological system. The flexibility of neural networks enables them to explore more complex nonlinear relationships in experimental data. Nevertheless, these neural systems have some problems intrinsic to its structural design, such as overtraining, overfitting, and network optimization. The other problem with application of neural networks concerns the reproducibility of results, due largely to random initialization of the networks and variation of stopping criteria. Consequently, there is a continuing need for the application of more accurateand revealing techniques in QSPR analysis. The support vector machine (SVM) is a new algorithm developed from the machine learning community16,17. SVM approach automatically controls the flexibility of the resulting classifier on the training data. Additionally, the deteriorating influence of the input dimensionality on the generalization ability is largely suppressed by the design of the algorithm. Due to its outstanding generalization performance, the SVM have attracted attention and gained extensive pharmaceutical applications, e.g., QSPR studies18,19, classification of pharmacokinetic properties of drugs20, drug design21, prediction of protein structure22, identifying genes23, and diagnose diseases24, etc. In most of these cases, the performance of SVM modeling either matches or is significantly better than that of traditional machine learning approaches.

In the current study, SVM was accomplished to describe the logBB of 310 drugs and organic compounds. The main purpose of the present study was to construct a QSPR model that could be used for the prediction of logBB of a various set of compounds from exclusively molecular structure considerations. A secondary aim was to exhibit the flexible modeling aptitude of SVM. The enhancement replacement method (ERM) was also employed to build quantitative linear relationship to compare with the results obtained by SVM.

2 Materials and methods

2.1 Experimental data set

The dataset considered in this study has been composed of blood-to-brain barrier partitioning behavior (logBB) of 310 drugs and organic compounds which were extracted from the values reported by Muehlbacher et al.25. Names and values of logBB for these compounds are collected in Table S1 (in Supporting Information). As can be seen in Table S1, the logBB values fall in the range of -2.15 to 1.60 for cetirizine and sertraline, respectively. Adjusting the parameters of models, a training set of 200 molecules was subtracted and remaining 110 molecules were used to evaluate the model prediction capability.

2.2 Molecular descriptor calculation and screening

In QSPR studies, chemical compounds must be represented using numerical molecular descriptors, which encode information from the chemical structure in a mathematical form. Determining the molecular descriptors of a chemical compound, initially the structure of the molecules were drawn using Hyperchem package (Version 7.0)26and the final geometries were achieved by means of the semi-empirical PM6 method. Subsequently, Dragon package (Version 3)27was used to calculate more than 1400 molecular descriptors, from 18 diverse kinds of theoretical descriptor for each molecule.

The prescreening of descriptors was done by removal of constant or near-constant descriptors. Since correlated descriptors encode comparable information about the chemicals, consequently, descriptors that display a higher correlation (R ＞ 0.90) with each other were recognized and only one of them that have higher correlation with the log BB was remained. Lastly, the descriptors were reduced to 285.

2.3 Variable selection using enhanced replacement method

An essential step in the development of a QSPR model is optimizing the number of descriptors to be comprised in the QSPR equation. In present study enhanced replacement method (ERM) was used as a novel and robust variable selection technique. ERM algorithm provides determining an ideal subset of descriptors from a great dataset of descriptors and N objects by use of MLR method. While attained identical results, ERM needs smaller number of linear regressions than a time-consuming Full Search methods28. ERM algorithm includes of the following steps29:

1. Nominating a primary set of descriptor d from D, randomly. Based on d, a MLR model is built. Consistent with the succeeding equation, the residual standard deviation (RSD) of the model is calculated:

where, N is the number of data points in the training data set and resiis the difference between the experimental and predicted value for the data point i in the training data set.

2. One of the descriptors in the primary set is replaced by all the remaining D-d descriptors one by one. In each replacement, a new multi-linear regression model is created and using Eq.(2), RSD for the built model is calculated. Then, the set with the larger RSD value is earmarked, considering the two sets of descriptors directed to the regression with the smallest values of RSD.

3. From the consequential set of descriptors in the previous step, the descriptor with the highest standard deviation in its coefficient is selected and replaced with all remaining D-d descriptors, one by one. It should be noted that in each sequence, the descriptor altered before is retained constant in the next step. This process is followed repeatedly until the descriptor set, d, remains unchanged.

ERM variable selection methods were performed using QSAR/QSPR Search Algorithms Toolbox. All calculations were performed in the MATLAB (Version 7.0)30.

2.4 Support vector machine

Support vector machines (SVMs) were suggested by Vapnik in the late 1960s. SVM is an original category of machine learning technique based on the statistical learning theory, which can solve the useful problems of small samples and nonlinearity. Since they are a talented estimator in data-driven fields, they have received imperative attention of researchers in QSAR/QSPR studies31-34. The basic idea is to plan the inventive data into a higher dimensional feature space by means of a kernel function and then creating a most favorable separating hyperplane, SVM performs classification in this space35. The comprehensive theory of SVM has been given inthe literature36,37. Principally, SVMs estimated the function with three different features: (1) approximation of the regression in a set of linear functions, (2) defining the regression approximation as the problem of risk minimization regarding the ε- insensitive loss function and (3) minimizing the risk based on the SRM principle whereby elements of the structure are defined by the inequality 1/2|ω|2≤ constant38. The linear function is formulated in the high-dimensional feature space, with the form of function (Eq.(3)).

2.5 Genetic algorithm

Genetic algorithm (GA) is a very popular optimization algorithm, which is based on a direct analogy to Darwinian evolutionary ideas of natural selection and genetics in biological systems40. GA has been effectively applied to a variety of different problems such as data mining and optimization. Recently it has also been used for the feature selection in SVM modeling.

Genetic algorithm always coexists with other classification and / or regression techniques, which play the role of fitness function. Generally, the process of GA proceeds as follows. First, GA produces an initial population consisting of a set of solutions randomly, where each solution is called a chromosome. For variable selection, each chromosome is typically represented in the form of binary string, with 1 and 0 representing selected and non-selected descriptors, respectively. After generating and assessing the initial population of chromosomes, the process of reproduction takes place on the basis of the results of certain fitness function, while offspring of these chromosomes are generated based on the notion of survival of the fittest. Note that the value of the fitness for each chromosome is calculated by leave-one-out cross-validation (LOOCV) in this study. Generally, the next population is resulted from genetic manipulation of the chromosomes in the current population through selection, recombination and / or mutation according to their fitness function. Generation of new populations would be repeated until an acceptable solution is obtained. The GA program was written in MATLAB (version 7.0).

2.6 Applicability domain

在特性上，风景园林行业相关安全技术规范规定了园林绿地建设的基本要求，不涉及技术细节。而各类标准则是法规标准体系的技术支撑，数量众多，涉及的内容十分广泛。规范与各类标准相互融合、互不排斥、协调发展，构成和谐统一的体系。

Acquiring reliable predictions for external samples, the applicability domain (AD) for the QSAR/QSPR models was developed. The AD provides the assessment of the uncertainty in the estimation of the similarity of a specific molecule to the compounds used to construct the model41-43.

In present study, the Williams plot, which provides a plot of standardized residuals versus the leverage values, was performed to evaluate the AD of the QSPR model. The leverage value (h) measures the distance from the centroid of the training set and hifor the ith compound is calculated from the descriptor matrix (X) as follows44:

where is a row vector of descriptors for ith compound; X is the matrix of descriptors for the training set. The leverage is appropriate for assessing the degree of extrapolation, its limit of normal values is set as:

where p is the number of descriptors involved in the model, and n is the number of compounds in the training set.

Leverage greater than h* for the training set means that the chemical is highly powerful in determining the model, while for the prediction set, it means that the prediction is the result of considerable extrapolation of the model and may not be consistent.

2.7 Model validation

Any model desires to be validated before it is performed for“understanding” or for predicting new parameters such as log BB of new compounds. So, one of the most important processes in QSPR studies is model validation45. Model validation can be categorized into internal validation and external validation. Generally, Y-random verification, leave-one-out cross-validation and bootstrapping are used for internal verification of QSPR model. However, external validation is to assess the predictive capability of model by the corresponding statistical parameters. In our work, leave-one-out cross-validation was used for internal validation, while the method recommended by literature46,47was adopted to validate the model.

2.7.1 Internal validation

In present study, the coefficient of determination (R2) and the root mean square error of calibration or training (RMSEC) were used to measure the fitness of the constructed model.

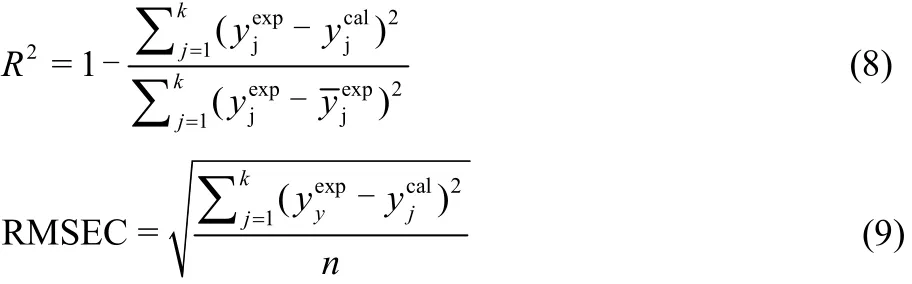
LOOCV was applied for the training set to measure the robustness of the models and to decrease the opportunity of the model over-fitting. The robustness of the developed models was assessed using calculation of the cross validation correlation coefficient(Eq.(10)) and cross validation root mean square error (RMSECV) (Eq.(11)).

2.7.2 External validation

Verifying the ability of model to predict the logBB of new compounds, the external validation technique was performed for the prediction set. As the measures of the predictive power of the models, the determination coefficient of prediction of prediction set (R2) and the root mean square error of prediction (RMSEP) were calculated using following equations:

In addition, considering a special QSPR model should be highly predictive, the conditions suggested by Golbraikh and Tropsha48were also employed for prediction set to extra confirmation of the predictive ability.

Here the parameters are represented as follows:

where yexpand ycalare the experimental and the calculated values, respectively; y¯trais the average value of the training set. R2is the correlation coefficient between the experimental and calculated values in the prediction set,andare the coefficients of determination, and k and k′ are slopes of regression lines through the origin of calculated versus experimental and experimental versus calculated, respectively. y¯caland y¯expare the mean values of the calculated and experimental values of the prediction set, respectively.

3 Results and discussion

3.1 Molecular diversity analysis

An influential QSPR model capable of estimation new compounds should be based on principally diverse chemicals in the training data and therefore, for a general model development, it is significant to determine the structural diversity of a dataset49. In order to perform this process, the Euclidean distance between each two molecules of i and j in selected descriptor space, (dij), was computed according to following equation:

In the above equation, m is the number of descriptors in descriptor matrix, and n is the number of molecules. The parameters of and are the kth descriptors of i and j molecules, respectively. In the next step the mean distances of one molecule to other molecules ( ) were computed according to:

Then the mean distances were normalized within the interval of zero to one and plotted against the logBB of chemicals as can be seen in Fig.1. Scattering of the chemicals in this plot specifies that the training and prediction sets are illustrative of the entire data set. The training set with a comprehensive representation of the chemistry space was adequate to confirm models' stability and the diversity of prediction set can evidence the predictive skill of the model.

3.2 Linear modeling

After the pre-reduction step of the descriptors calculated by Dragon, totally 285 descriptors were reserved for each compound. To select the best descriptor subset, 285 descriptors were used as inputs for ERM variable selection technique. When adding extra variable did not improve the performance of the model considerably, it means that the ideal subset size wasachieved. Finally, a 6-variables model was selected as the optimal ERM model. The regression equation of the best model was as follows:

Fig.1 Results of diversity analysis

Table 1 shows the specifications of selected ERM model. The multi-collinearity between the above six descriptors were identified by calculating their variation inflation factors (VIF), which can be calculated as follows:

where R is the correlation coefficient of the multiple regression between the variables in the model. If VIF equals to 1, then no inter-correlation exists for each variable; if VIF falls into the range of 1-5, the related model is satisfactory; and if VIF is larger than 5, the related model is unsteady and a considerable recheck would be mandatory50. The corresponding VIF values of the five descriptors are shown in last column of Table 1. As can be seen from this Table, all the implemented variables have VIF values of less than 5, representing that the achieved model has satisfied statistical results.

To examine the comparative significance in addition to the influence of each descriptor in the model, for each descriptor, the value of the mean effect (MF) was calculated using the equation below (Eq.(27)):

In this equation, MFjsignifies the mean effect for the considered descriptor j, βjis the coefficient of the descriptor j, dijstands for the value of the target descriptors for each molecule and m is the number of the descriptors in the model51. The MF value represents the relative significance of each descriptor compared with the other ones in the recommended model. Its sign displays the variation direction in the values of the properties owing to the increase (or reduction) of this descriptor values. Table 2 shows the correlation matrix between selected descriptors which are orthogonal and independent (R ＜0.5) that they were used in development of QSPR models.

The data set and corresponding ERM predicted values of the log BB for all molecules studied in this investigation were reported in Table S1 (in Supporting Information).

Table 1 Specification of selected enhanced replacement method ERM

Table 2 Correlation matrix for descriptors applying in this work

As it was shown in the statistical parameters of ERM model (Table 3), the determination coefficient, R2was 0.870 and RMSEC was 0.262, indicating the model was with good fitness ability. The model was carried out to perform the LOOCV with the correlation coefficientof 0.865, and the RMSECV of 0.278, implying the reliability and robustness of the ERM model. Then, the model was used to predict the external prediction set, the determination coefficient of prediction R2was 0.878 and RMSEP was 0.228, which showed that this ERM model can be used to predict the log BB of drugs and organic compounds. This method yields an overall prediction accuracy of 90.4%.

Table 3 Comparison of the validation parameters of SVM and ERM models

3.3 Nonlinear modeling

Nonlinear technique SVM was also employed to explore the intrinsic nonlinearity between the structures of organic compounds and logBB. The selected descriptors by ERM were introduced as the input variables to establish the SVM model.

Considering the excellent feature selection ability of GA and the robust modeling performance of SVM, non-linear regression model based on SVR was built. Generally, GA-SVR is not computationally more costly in searching the best combination of descriptors using GA, except that the algorithm of SVR is much more sophisticated and more time may be needed. However, it is very repentant to point out that although SVM has been successfully introduced into many research fields including QSPR, a few of the researches were devoted to the simultaneous optimization of the parameters of kernel function and cost (C) involved in the established model, cutting down the probability of achieving the global optimum.

In this model, radial bias function (RBF) was used as Kernel function and the values of capacity parameter (C), epsilon (ε), and the Kernel parameter (γ) optimized. For optimizing these parameters, their values were changed in the range of 10-100 for C, 0.01-0.1 for ε and 0.1-1 for γ, and the efficiency of SVMs was checked.

The detail parameter setting for genetic algorithm is as the following: population size 500, crossover rate 0.7, mutation rate 0.02, two-point crossover, roulette wheel selection, and elitism replacement. The termination criteria are that the generation number reaches generation 1000 or that the fitness value does not improve during the last 100 generations. The best chromosome is obtained when the termination criteria satisfy. Using genetic algorithm, the optimized values of C, γ and ε are obtained 60, 0.4 and 0.03, respectively.

Table S1 presents the SVM predicted values of the logBB for all molecules studied in this study. The statistical parameters of SVM model were listed in Table 3. The corresponding correlation coefficient of 0.990 for the training set, 0.988 for the cross validation and 0.986 for the prediction set, RMSE were 0.072, 0.073 and 0.074, respectively. This method yields an overall prediction accuracy of 93.1%. Fig.2 shows the plot of the SVM predicted versus experimental values for log BB of all of the molecules in data set. The residuals of the SVM calculated values of the logBB are plotted against the experimental values in Fig.3. The propagation of the residuals in both sides of zero line indicates that no systematic error exists in the constructed QSPR model.

3.4 Descriptors interpretation

From a practical opinion, interpreting the descriptors applied in the models could provide some insight into factors that are probable to administer the logBB and help us comprehend which interactions may play an essential role in blood-brain distribution of drugs and organic compounds.

The descriptors presented in this QSPR model are: average valence connectivity index chi-4 (X4av), Balaban centric index (BAC), average information content (order 1) (IC1), dCoMMA2 value/weighted by atomic van der waals volumes (DISPv), leverage-weighted autocorrelation of lag 7/weighted by atomic polarizabilities (Hats7p) and 3D-morse signal 04 /weighted by atomic masses (mor04m).

For evaluation of the relative significance and influence of each descriptor in the model, the value of mean effect (MF) was calculated and shown in Table 1. MF presented in this Table, permits allocating a greater importance to those molecular descriptors with larger absolute mean effect values. The model descriptors significance decreases in the following order:

Fig.2 Plot of SVM calculated versus experimental values of blood-to-brain barrier partitioning color online

Fig.3 Plot of SVM residual versus experimental values of blood-to-brain barrier partitioning color online

The first descriptor according to its mean effect is average information content (order 1) (IC1) which is a topological descriptor. The average information content is defined on the basis of the Shannon information theory and is calculated as follows52,53:

where niis a number of atoms in the ith class and n is a total number of atoms in the molecule. The division of atoms into different classes depends upon the coordination sphere taken into account. This leads to the indices of different order k. The information content (IC) is equal to average information content multiplied by the total number of atoms.

The second descriptor is leverage-weighted autocorrelation of lag 7/weighted by atomic polarizabilities (Hats7p). This descriptor is an H-GETAWAY descriptor, which is calculated from the molecular influence matrix (MIM) H. The MIM H contains some useful information on the molecular geometry and especially the diagonal elements (leverages) of the matrix allow discriminating among the atoms according to their position in the 3D molecular space with respect to the molecule centre54,55. This descriptor is calculated as follows:

HATS indices are based only on the diagonal elements of the MIM, which account for the relative position of each atom in the 3D molecular space.

D COMMA 2 value/weighted by atomic van der Waals volumes (DISPV) is a geometrical descriptor which calculates different molecular moments with respect to the center of mass56.

Next descriptor according to mean effect is Balaban centric index (BAC). BAC is a topological index defined for acyclic graphs based on the pruning of the graph, a stepwise procedure for removing all the terminal vertices, i.e. vertices with a vertex degree of one (δi = l), and the corresponding incident edges from the H-depleted molecular graph G. The vertices and edges removed at the gth step are ngand the total number of steps to remove all vertices is R57.

Average valence connectivity index of order 4 (X4Av) is a molecular valence connectivity index able to account for the presence of heteroatoms in the molecule as well as double and triple bonds. The details of their definition and the calculation method can be found elsewhere58-60. The general expression for the mth-order molecular valence connectivity index is as follows:

where m is the order of the molecular valence connectivity index, k denotes a contiguous path type of fragment, which is divided into paths (P), cluster (C), path-clusters (PC), and chains (cycles) (CH). nmis the number of the relevant paths, andis the atomic valence connectivity index and is defined as:

where s represents the scattering in various directions by a collection of A atoms located at points ri; fi is a form factor taking into account the direction dependence of scattering from a spherical body of finite size. The scattering value s measures the scattering angle as:

where Ziis the number of electrons of atom i, Zivis the number of valence electrons, and hiis the number of hydrogen connected with atom i.

The last descriptor described here is mor04m. 3D-MORSE descriptors (3D-Molecule Representation of Structures based on Electron diffraction are based on the idea of obtaining information from the 3D atomic coordinates by the transform used in electron diffraction studies for preparing theoretical scattering curves61. A generalized scattering function, called the molecular transform, can be used as the functional basis for deriving, from a known molecular structure, the specific analytic relationship of both X-ray and electron diffraction. The general molecular transform is:

where ν is the scattering angle and λ is the wavelength of the electron beam.

Usually, the above equation is used in a modified form as suggested in 1931 by Wierl62. On substituting the form factors by the atomic property w, considering the molecule to be rigid and setting the instrumental constant equal to one, the following expression is obtained:

where I(s) is the scattered electron intensity, w is an atomic property (in this case atomic masses), chosen as the atomic number, rjiare the interatomic distances between the ith and jth atoms, respectively, and A is the number of atoms.

From these descriptors, X4av, DISPv, Hats7p and mor04m have positive signs for their mean effect. The positive values of these four descriptors in the QSPR model specify that these descriptors contribute positively to values of logBB. The remaining descriptors have negative signs. The negative signs of mean effect for these two descriptors indicate that as the values of these descriptors increase, the values of logBB decrease.

From the above discussion, it can be detected that all descriptors included in the QSPR model have physical meaning, and that these descriptors can account for structural features affecting the logBB of the interested molecules.

3.5 Comparison of the results attained by different QSPR methodologies

Fig.4 Williams plot of standardized residuals versus leverages of descriptors matrix by ERM model

Fig.5 Williams plot of standardized residuals versus leverages of descriptors matrix by SVM model

The results of different QSPR models are collected in Table 3. The correlation coefficient (R2) between experimental and predicted logBB by ERM and SVM are 0.870 and 0.990, respectively, for training set and 0.878 and 0.986, respectively for the prediction set. The standard errors of training and prediction sets for the ERM model are 0.262 and 0.228, respectively which would be compared with the values of 0.072 and 0.074, respectively, for the SVM model. As can be seen from Table 3, the result of SVM model is superior to those attained by ERM method. Comparison of the results achieved by SVM to those obtained by ERM method, we found that the SVM executed better than the other method. It also established the improved generalization aptitude for SVM, and showed that SVM can be used as an influential chemometrics tool for QSPR inquiries.

3.6 Applicability domain analysis

The domain of applicability describes the consistency boundaries for a model. It is a plot of predictive aptitude (standardized cross validated residuals) versus the leverage of a model, and also recognized as the William plot. The Williams plot was used to instinctively demonstrate a visual image of the outliers: the response outliers (Y outliers) and the structurally influential compounds (X outliers). The Y outliers are those compounds that their standardized residuals are greater than 3.0 standard deviation units (＞ 3 s) while the leverage value hiis relatively low. The X outliers are compounds with the leverage values greater than the threshold value (hi＞ h*) meanwhile the relatively low standard deviation63.

To imagine the applicability domain of ERM and SVM models, the William's plots were characterized for training and prediction sets in Figs.4 and 5 respectively. In these plots, the vertical line specifies the limit of X outliers is determined by the warning leverage value (h*). As can be seen in this figure, no compound has leverage value greater than the cutoff value of h* = 0.09. The horizontal lines describe the compound with standardized residuals greater than 3 standard deviation units is an outlier. As can be seen in these figures, all chemicals in the prediction set are in the applicability domain of models and there is no outlier response compound for prediction sets, which demonstrates the reliability of the predictions.

3.7 External validation result

In order to estimate the predictive authority of the proposed models using different methods, external validation technique was carried as explained in ‘‘Materials and methods’’ section. The results of validation recommended by Golbraikh and Tropsha for the external prediction set were listed in Table 4.0.878 ＞ 0.6, 0.85 ＜ k = 0.874 ＜ 1.15, 0.85 ＜ k'2= 1.023 ＜ 1.15,ERM model.

As the results indicate, all of the models are valid with acceptable and reasonable predictability. As mentioned above, the best model was obtained based on SVM model. It could be concluded that the result of external validation for the prediction set satisfied Golbraikh and Tropsha's condition, thus further verifying the predictability for the prediction set in SVM model.

Table 4 Statistical criteria of external validation prediction set of the proposed QSPR models

3.8 Comparison of our model with other different models

Kortagere et al. apply a generalized regression model and support vector machine (SVM) models with Shape Signatures descriptors, to predict blood-brain barrier (BBB)64. Their regression model was tested on 100 molecules not in the model and resulted in a correlation r2= 0.65. The developed SVM models with molecular operating environment (MOE) descriptors were superior to regression models, while Shape Signatures SVM models were comparable or better than those with MOE descriptors. The best 2D shape signature models had10-fold cross validation prediction accuracy between 80%-83% and leave-20%-out testing prediction accuracy between 80%-82% as well as correctly predicting 84% of BBB+ compounds (n = 95) in an external database of drugs.

Li et al. used logistic regression, linear discriminate analysis, k nearest neighbor, C4.5 decision tree, probabilistic neural network and support vector machine for prediction of blood-brain barrier penetrating and nonpenetrating agents65. Computational methods have been employed for the prediction of BBB-penetrating (BBB+) and -nonpenetrating (BBB-) agents at impressive accuracies of 75%-92% and 60%-80%, respectively.

Gerebtzoff and Seelig performed the calculated molecular cross-sectional area as main parameter for in silico prediction of blood-brain barrier permeation66. The predictive value of the parameter ADcalcM, for the BBB permeation, was then tested with different data sets, revealing that the calculated cross-sectional area alone correctly predicted 83.3% of blood-brain barrier permeation on the first data set, 74.4% for the second data set, and 71.4% for the third data set. Together with the calculated logD7.4, the prediction accuracy for the present set of 122 different drugs increased to 90.2%.

Muehlbacher et al. applied quantitative in silico techniques to predict BBB permeability. For this purpose they created a reasonably large dataset (n = 362) of experimental logBB values67. For each compound of the training set, they calculated a broad set of descriptors ranging from simple atom count descriptors to computational more expensive descriptors like the CSA perdendicular to the amphiphilic axis.

The best quantitative prediction system based on multiple linear regression without overfitting yielded a squared correlation coefficient of 0.521. Qualitative models based on a random forest performed remarkably better. The best prediction system based on only four descriptors achieved a bootstrap validated accuracy of 88%.

The comparison between these models and our model is shown in Table 5. As can be seen in this table, the overall prediction accuracy of our QSPR models are superior to those obtained by others.

Table 5 Comparison between other models with our developed models

4 Conclusions

In this study, ERM and SVM were utilized to develop linear and nonlinear QSPR-based models for successful prediction of logBB of various drugs and organic compounds. The built models clearly display good correlations between the structure and logBB of the studied compounds. The calculated statistical parameters of these models disclose the superiority of SVM over ERM model. The result indicates that SVM model can precisely explain the relationship between the structural parameters and blood-brain distribution of drugs and organic compounds. This study of the QSPR model shows that the SVM proved to be a very promising tool in the prediction of logBB. By performing model validation, it can be determined that the presented model is an appropriate model and can be effectively used to predict the logBB of drugs and organic compounds with accuracy close to the accuracy of experimental logBB determination.

Supporting Information: available free of charge via the internet at http://www.whxb.pku.edu.cn.

(1) Goldstein, G. W.; Betz, A. L. Sci. Am. 1986, 255, 74. doi: 10.1038/scientificamerican0986-74

(2) Greig, N. H.; Brossi, A.; Pei, X. F.; Ingram, D. K.; Soncrant, T. T. New Concepts of a Blood-Brain Barrier; Plenum: New York, NY, 1995; pp 251-264. doi: 10.1007/978-1-4899-1054-7-25

(3) Weiss, N.; Miller, F.; Cazaubon, S.; Couraud, P. O. Rev. Neurol. 2009, 165, 1010. doi: 10.1016/j.neurol.2009.04.013.

(4) Partridge, W. M. J. Neurochem. 1998, 70, 1781.doi: 10.1046/j.1471-4159.1998.70051781.x

(5) Pardridge, W. M. Drug Discov. Today 2001, 6, 1. doi: 10.1016/S1359-6446(00)01583-X

(6) Tamai, I.; Tsuji, A. Adv. Drug. Deliv. Rev. 1996, 19, 401. doi: 10.1016/0169-409X(96)00011-7

(7) Eddy, E. P.; Maleef, B. E.; Hart, T. K.; Smith, P. L. Adv. Drug Deliv. Rev. 1997, 23, 185. doi: 10.1016/S0169-409X(96)00435-8

(8) Reichel, A.; Begley, D. J. Pharm. Res. 1998, 15, 1270. doi: 10.1023/A:1011904311149

(9) Cecchelli, R.; Dehouck, B.; Descamps, L.; Fenart, L.; Buee-Scherrer, V.; Duhem, C.; Landquist, S.; Rentfel, M.; Torpier, G.; Dehouck, M. P. Adv. Drug Deliv. Rev. 1999, 36, 165. doi: 10.1016/S0169-409X(98)00083-0

(10) Bujak, R.; Struck-Lewicka, W.; Kaliszan, M.; Kaliszan, R.; Markuszewski, M. J. J. Pharm. Bio. Anal. 2015, 108, 29. doi: 10.1016/j.jpba.2015.01.046

(11) Konovalov, D. A.; Coomans, D.; Deconinck, E.; Vander Heyden, Y. J. Chem. Inf. Model. 2007, 47, 1648. doi: 10.1021/ci700100f

(12) Nikolic, K.; Filipic, S.; Smoliński, A.; Kaliszan, R.; Agbaba, D. J. Pharm. Pharm. Sci. 2013, 166, 22. doi: 10.18433/J3JK5P

(13) Shityakov, S.; Neuhaus, W.; Dandekar, T.; Förster, C. Int. J. Comput. Bio. Dr. Desig. 2013, 6, 146. doi: 10.1504/IJCBDD.2013.052195

(14) Hemmateenejad, B.; Miri, R.; Safarpour, M. A.; Mehdipour, A. R. J. Comput. Chem. 2006, 72, 1125. doi: 10.1002/jcc.20437

(15) Guerra, A.; Páez, J. A.; Campillo, N. E. Mol. Inf. 2008, 27, 586. doi: 10.1002/qsar.200710019

(16) Vapnik, V. Estimation of Dependencies Based on Empirical Data; Springer: Berlin, 1982. doi: 10.1007/0-387-34239-7

(17) Burges, C. J. C. Data Min. Knowl. Disc. 1998, 2, 121. doi: 10.1023/A:1009715923555

(18) Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W. E., Jr. Mol. Inf. 2012, 31, 867. doi: 10.1002/minf.201200091

(19) Zhang, L.; Zhu, H.; Oprea, T. I.; Golbraikh, A.; Tropsha, A. Pharm. Res. 2008, 25, 1902. doi: 10.1007/s11095-008-9609-0

(20) Yang, S.; Huang, Q.; Li, L. L.; Ma, C. Y.; Zhang, H.; Bai, R.; Teng, Q. Z.; Xiang, M. L.; Wei, Y. Q. Art. Intel. Med. 2009, 46, 155. doi: 10.1016/j.artmed.2008.07.001

(21) Norinder, U. Neurocomuting 2003, 55, 337. doi: 10.1016/S0925-2312(03)00374-6

(22) Cai, Y. D.; Liu, X. J.; Xu, X. B.; Chou, K. C. Comput. Chem. 2002, 26, 293. doi: 10.1016/S0097-8485(01)00113-9

(23) Bao, L.; Sun, Z. R. FEBS Lett. 2002, 521, 109. doi: 10.1016/S0014-5793(02)02835-1

(24) Zhao, C. Y.; Zhang, R. S.; Liu, H. X.; Xue, C. X.; Zhao, S. G.; Zhou, X. F.; Liu, M. C.; Fan, B. T. J. Chem. Inf. Comput. Sci. 2004, 44, 2040. doi: 10.1021/ci049877y

(25) Muehlbacher, M.; Spitzer, G. M.; Liedl, K. R.; Kornhuber, J. J. Comput. Aided Mol. Des. 2011, 25, 1095. doi: 10.1007/s10822-011-9478-1

(26) Hyperchem, Re. 4. for Windows; Autodesk: Sansalito, CA, 1995.

(27) Todeschini, R.; Consonni, V.; Pavan, M. Dragon Software; Talete SRL: Milan, Italy, 2002.

(28) Levet, A.; Bordes, C.; Clément, Y.; Mignon, P.; Chermette, H.; Marote, P.; Cren-Olivé, C.; Lantéri, P. Chemosphere 2013, 93, 1094. doi: 10.1016/j.chemosphere.2013.06.002

(29) Duchowicz, P. R.; Castro, E. A.; Fernández, F. M.; González, M. P. Chem. Phys. Lett. 2005, 412, 376. doi: 10.1016/j.cplett.2005.07.016 (30) MATLAB 7.0, The Mathworks Inc.: Natick, MA, USA, 2005, http://www.mathworks.com.

(31) Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W. E., Jr. Struct. Chem. 2013, 24, 1799. doi: 10.1007/s11224-013-0222-4

(32) Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W. E., Jr. Phys. Chem. Liq. 2013, 51, 182. doi: 10.1080/00319104.2012.708932

(33) Dashtbozorgi, Z.; Golmohammadi, H.; Acree, W. E., Jr. Thermochim. Acta 2012, 539, 7. doi: 10.1016/j.tca.2012.03.017

(34) Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W. E., Jr. Mol. Inf. 2012, 31, 867. doi: 10.1002/minf.201200091

(35) Zhou, X.; Li, Z.; Dai, Z.; Zou, X. J. Mol. Graph. Model. 2010, 29, 188. doi: 10.1016/j.jmgm.2010.06.002

(36) Miao, Y.; Su, H.; Xu, O.; Chu, J. Ind. Eng. Chem. Res. 2009, 48, 10903. doi: 10.1021/ie801629f

(37) Li, H.; Liang, Y.; Xu, Q. Chemometr. Intell. Lab. Syst. 2009, 95, 188. doi: 10.1016/j.chemolab.2008.10.007

(38) Rojas, C.; Duchowicz, P. R.; Tripaldi, P.; Pis Diez, R. Chemometr. Intell. Lab. Syst. 2015, 140, 126. doi: 10.1016/j.chemolab.2014.09.020

(39) Mercader, G.; Duchowicz, P. R.; Fernández, F. M.; Castro, E. A. Chemometr. Intell. Lab. Syst. 2008, 92, 138. doi: 10.1016/j.chemolab.2008.02.005

(40) Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York: 1991. doi: 10.1017/S0269888900006068

(41) Cao, D. S.; Liang, Y. Z.; Xu, Q. S.; Li, H. D.; Chen, X. J. Comput. Chem. 2010, 31, 592. doi: 10.1002/jcc.21351

(42) Yan, J.; Huang, J. H.; He, M.; Lu, H. B.; Yang, R.; Kong, B.; Xu, Q. S.; Liang, Y. Z. J. Sep. Sci. 2013, 36, 2464. doi: 10.1002/jssc.201300254

(43) Cao, D. S.; Liang, Y. Z.; Xu, Q. S.; Yun, Y. H.; Li, H. D. J. Comput. Aided Mol. Des. 2011, 25, 67. doi: 10.1007/s10822-010-9401-1

(44) Eriksson, L.; Jaworska, J.; Worth, A. P.; Cronin, M. T.; McDowell, R. M.; Gramatica, P. Health Perspect. 2003, 111, 1361. doi: 10.1289/ehp.5758

(45) Golbraikh, A.; Shen, M.; Xiao, Z.; Xiao, Y.; Lee, K. H.; Tropsha, A.J. Comput. Aided Mol. Des. 2003, 17, 241. doi: 10.1023/A:1025386326946

(46) Tang, K.; Li, T. Anal. Chim. Acta 2003, 476, 85. doi: 10.1016/S0003-2670(02)01257-6

(47) de Campos, L. J.; de Melo, E. B. J. Mol. Graph. Model. 2014, 54, 19. doi: 10.1016/j.jmgm.2014.08.004

(48) Golbraikh, A.; Tropsha, A. J. Mol. Graph. Model. 2002, 20, 269. doi: 10.1016/S1093-3263(01)00123-1

(49) Zhao, C. Y.; Zhang, H. X.; Zhang, X. Y. ; Liu, M. C.; Hu, Z. D.; Fan, B. T. Toxicol. 2006, 217, 105. doi: 10.1016/j.tox.2005.08.019

(50) Agrawal, V. K.; Khadikar, P. V. Bioorg. Med. Chem. 2001, 911, 3035. doi: 10.1016/S0968-0896(01)00211-5

(51) Pourbasheer, E.; Riahi, S.; Ganjali, M. R.; Norouzi, P. J. Enzyme. Inhib. Med. Chem. 2010, 256, 844. doi: 10.3109/14756361003757893

(52) Kier, L. B. J. Pharm. Sci. 1980, 69, 807. doi: 10.1002/jps.2600690914

(53) Bonchev, D. Information Theoretic Indices for Characterization of Chemical Structure; Wiley-Interscience: New York, 1983. doi: 10.1002/jps.2600730950

(54) Sliwoski, G.; Mendenhall, J.; Meiler, J. J. Comput. Aided Mol. Des. 2016, 30, 209. doi: 10.1007/s10822-015-9893-9

(55) Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors, In: Methods and Principles in Medicinal Chemistry; Mannhold, R., Kubinyi, H., Timmerman, H. Eds.; Wiley-VCH: Weinheim, 2000. doi: 10.1002/9783527613106

(56) Silverman, B. D.; Platt, D. E. J. Med. Chem. 1996, 39, 2129. doi: 10.1021/jm950589q

(57) Balaban, A. T. Theor. Chim. Acta 1979, 53, 355. doi: 10.1007/BF00555695

(58) Kier, L. B.; Hall, L. H. Molecular Connectivity in Structure-Activity Analysis; Wiley: New York, 1986. doi: 10.1002/aic.690331230

(59) Hall, L. H.; Kier, L. B. J. Mol. Graph. Model. 2001, 20, 4. doi: 10.1016/S1093-3263(01)00097-3

(60) Randic, M. J. Mol. Graph. Model. 2001, 20, 19. doi: 10.1016/S1093-3263(01)00098-5

(61) Soltzberg, L. J.; Wilkins, C. L. J. Am. Chem. Soc. 1977, 99, 439. doi: 10.1021/ja00444a021

(62) Kovtun, D. M.; Kochikov, I. V.; Tarasov, Y. I. J. Phys. Chem. A 2015, 119, 1657. doi: 10.1021/jp5082774

(63) Ma, S.; Lv, M.; Deng, F.; Zhang, X.; Zhai, H.; Lv, W. J. Hazard. Mater. 2015, 283, 591. doi: 10.1016/j.jhazmat.2014.10.011

(64) Kortagere, S.; Chekmarev, D.; Welsh, W. J.; Ekins, S. Pharm. Res. 2008, 25, 1836. doi: 10.1007/s11095-008-9584-5

(65) Li, H.; Yap, C. W.; Ung, C. Y.; Xue, Y.; Cao, Z. W.; Chen, Y. Z. J. Chem. Inf. Model. 2005, 45, 1376. doi: 10.1021/ci050135u

(66) Gerebtzoff, G.; Seelig, A. J. Chem. Inf. Model. 2006, 46, 2638. doi: 10.1021/ci0600814

(67) Muehlbacher, M.; Spitzer, G. M.; Liedl, K. R.; Kornhuber, J. J. Comput. Aided Mol. Des. 2011, 25, 1095. doi: 10.1007/s10822-011-9478-1

10.3866/PKU.WHXB201704051

February 5, 2017; Revised: March 2, 2017; Published on Web: April 5, 2017.

＊Corresponding author. Email: Hassan.gol@gmail.com; Tel: +98-21-66518561; Fax: +98-21-66518561.

© Editorial office of Acta Physico-Chimica Sinica