锁相红外热像检测缺陷的定量方法
2017-06-21赵翰学周正干
李 根,赵翰学,范 瑾,周正干,2
(1.北京航空航天大学 机械工程及自动化学院, 北京 100083;2.先进航空发动机协同创新中心, 北京 100083)
锁相红外热像检测缺陷的定量方法
李 根1,赵翰学1,范 瑾1,周正干1,2
(1.北京航空航天大学 机械工程及自动化学院, 北京 100083;2.先进航空发动机协同创新中心, 北京 100083)
为了满足锁相红外热像检测中缺陷定量的需求,提出了一种基于模糊C均值聚类的算法(Fuzzy C-means,FCM)和边缘检测算子(Edge Detectors)的缺陷尺寸定量评价方法。制备了圆形平底孔钢材料试样,通过有限元仿真研究了最佳激励频率的选择方案,建立了锁相红外热像检测系统,开展了区域划分下的FCM-边缘检测算子联合处理方法的缺陷定量评价试验。区域划分下的FCM-边缘检测算子联合处理方法取得了与广泛认可的切相位法相当的缺陷定量结果;所得特征图像能反映更多的缺陷特征边缘信息,利用适当的图像处理方法,能够实现缺陷面积定量评价。结果表明:区域划分下的FCM-边缘检测算子缺陷定量评价方法在锁相红外热像检测领域具有良好的应用前景。
锁相红外热像检测;缺陷定量;最佳激励频率;FCM-边缘检测算子联合处理;切相位法
红外热成像检测技术(IRT)具有单次检测面积大、检测速度快、直观精确、非接触等特点,已逐步成为保证产品质量和安全的重要手段[1]。红外热成像检测技术可分为脉冲红外热像检测技术和锁相红外热像检测技术。相比于脉冲红外热像检测技术,锁相红外热像检测技术可检测的深度更深,对材料加热的不均匀性和环境因素均不敏感[2]。
缺陷的定量检测一直是锁相红外热像检测研究的重要课题之一。2008年,韩国的CHOI等[3]提出了针对锁相红外热像检测的缺陷定量方法——切相位法(Shearing Phase Method),并在实验室条件下利用该方法得到了误差范围在4%以内的缺陷定量结果。由于切相位法从相位值数据本身出发,通过切相位提取出缺陷边缘信息,因此该方法在锁相红外热像检测中已被广泛认可与运用[4-6]。此外,2012年刘俊岩等[7]提出利用归一化相位及其拟合分布的微分特征的方法对缺陷直径进行定量检测,得到了很好的定量结果。
在红外热成像检测领域,利用图像边缘检测技术提取红外检测图像中缺陷特征的边缘也是一种实现缺陷定量的手段。由于外界噪声的存在,红外检测图像通常会包含除缺陷特征信息以外的其他信息,导致直接使用如Roberts、Sobel、Prewitt、LOG、Canny等边缘检测算子很难得到理想的缺陷检测结果,难以用于缺陷的定量分析[8]。因此,近年来国内部分学者提出利用模糊C聚类均值算法(Fuzzy C-Means,FCM)对红外检测图像先进行图像分割,再通过边缘提取算子运算,以此达到提取缺陷特征边缘的目的[8-10]。从最终缺陷定量结果来看,对整个红外检测图像运用FCM算法存在着算法计算量过大[9]、部分缺陷信息缺失[10]的问题,同时,在参数选取上,聚类数目的选取存在着多样性。以上的问题都对FCM算法在锁相红外热像检测缺陷定量中的运用提出了挑战。
笔者进行了两方面的工作:一是提供了激励频率的选择方案,以保证锁相红外热像检测所得的相位图拥有最佳的缺陷检测能力;二是提出一种区域划分下的FCM-边缘检测算子联合处理方法,并与广泛使用且易实现的切相位方法所得的定量结果作比较,以此来阐述该方法在锁相红外热像检测中的有效性和优势。
1 相关理论
1.1 锁相红外热像检测
锁相红外热像检测技术的原理由德国斯图加特大学BUSSE教授[11]于1992年提出。
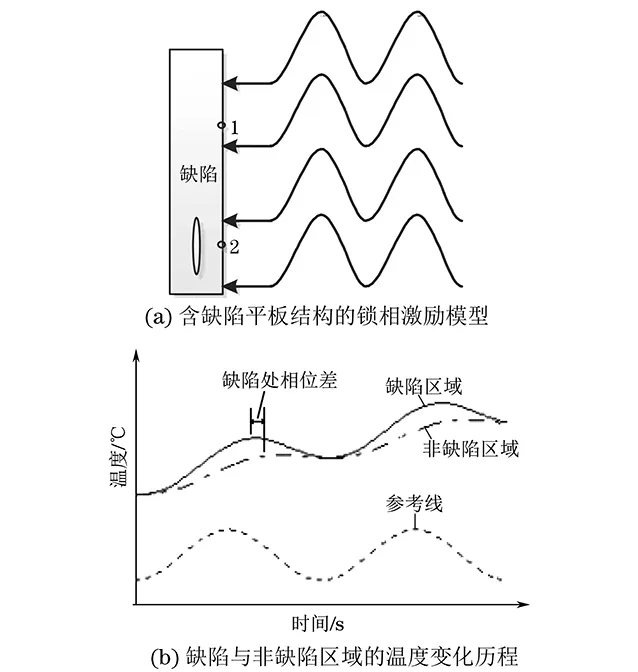
图1 锁相红外热像检测原理
锁相红外热像检测原理如图1所示,根据红外热像仪采集到的一系列红外温度图像,可得到试件表面上某点在整数倍激励周期下的温度数据在时间历程上的分布T(x,y,t),如式(1)所示。
式中:A(x,y,t)为表面每个点的温度的幅值,随时间的变化,其值会有所不同;φ(x,y)为每个点的表面温度的相位。
通过锁相算法,能够得到每个点温度的幅值和相位,继而得到幅值图和相位图。
锁相红外热像检测中,由于非缺陷区与缺陷特征处的热扩散程度不同,其温度的幅值和相位存在着差值。在幅值图和相位图中,这些差值反映为幅值图或相位图中像素灰度值间的差异,因此可以用幅值图和相位图来识别材料的缺陷。
1.2 切相位法原理
与幅值图相比,相位图更适合于材料内部缺陷的定量检测[12]。在相位图中,缺陷区域与非缺陷区域所对应的相位值之间的相位差Δφ为

式中:φd(x,y)为缺陷区域的像素点(x,y)对应的相位值;φs(xs,ys)为非缺陷区域的某个已知像素点(xs,ys)对应的相位值。对相位图中缺陷特征所在区域,切相位法求水平方向或垂直方向上邻近的两个像素点所对应的相位值之间的差值ΔφSP。
或
由此可得到所对应的切相位分布。每块缺陷特征所在区域都存在着切相位值的最大值、最小值和零点。切相位法规定这些最大值点和最小值点分别对应缺陷的边缘;而针对规则图形的缺陷,零点对应缺陷中心所在的位置。
1.3 经典模糊C均值聚类算法
经典模糊C均值聚类算法的基本思想是:将数据集X={x1,x2,…,xn}分为c类,X中的任意样本xi对j类的隶属度为uij(∈[0,1]),分类结果用模糊隶属度矩阵U=(uij)n×c来表示,聚类中心为V=(v1,…,vc)(c≥2)。FCM算法通过最小化关于隶属度矩阵U和聚类中心V的目标函数J(U,V;X)来实现,算法的迭代序列或其子序列必收敛到目标函数的一个极小值或者鞍点[13]。式(5)给出了目标函数的形式。
‖
式中:m为模糊加权指数,用于控制算法柔性;vj(1≤j≤c)为相应的聚类中心。
隶属度矩阵对应的模糊c划分空间为
M={U=[uij]n×c|∀i,∀j,uij∈[0,1],
式中:n为数据集X中数据数目;c为聚类中心数目。
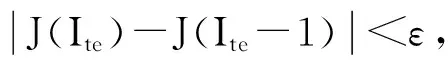
每次迭代都需通过式(7)和式(8)来分别更新聚类中心和隶属度:
2 试样和试验系统
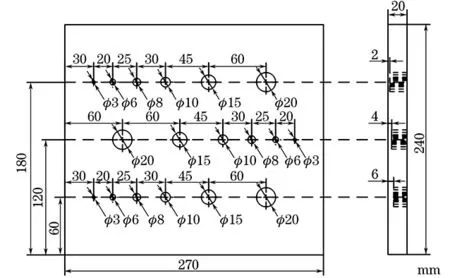
图2 Q235钢材料试样缺陷布局示意
利用预置了不同深度、不同尺寸的圆形平底孔缺陷的试样来进行缺陷尺寸定量研究。试样的缺陷布局如图2所示,按照GB/T 26643《无损检测 闪光灯激励红外热像法导则》制备缺陷。试样材料为Q235钢,其热扩散系数为1.37×10-5m2·s-1。对所需检测的缺陷进行编号,将深度为2 mm的平底孔缺陷由尺寸从大到小的顺序依次编号为A1、B1、C1、D1、E1、F1;深度为4 mm的平底孔缺陷由尺寸从大到小的顺序依次编号为A2、B2、C2、D2、E2、F2;深度为6 mm的平底孔缺陷由尺寸从大到小的顺序依次编号为A3、B3、C3、D3、E3、F3。
由于Q235钢的表面存在对可见光反射强且红外发射率低的问题,卤素灯激励时发射损失大,影响检测效果。为了提高试样的红外吸收率和发射率,在试样表面上涂抹了水溶性黑漆。
使用的锁相红外热像检测系统的构成如图3所示。系统由红外热像仪、系统控制端(计算机)、函数发生器、信号放大器和激励源(最大功率为1 kW的卤素灯)组成。卤素灯灯罩前沿距离试样大概40 cm左右,函数发生器产生信号需经功率放大器放大来控制卤素灯;该系统红外热像仪型号为SC7700M,工作波段为3.7~4.8 μm,灵敏度为0.018 K。
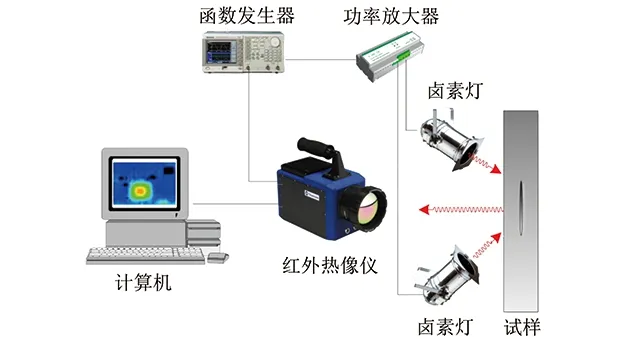
图3 锁相红外热像检测系统构成示意
3 激励频率优选
为了得到最好的定量检测结果,应选择最佳激励频率[14]。在最佳激励频率下,缺陷中心点与非缺陷区的相位差应是锁相红外热像检测中常用的激励频率区间中的极大值。
材料的锁相红外热像检测最佳激励频率的选择通常是基于实际试验得到的,因此通常很难从中得到一般的规律。而通过有限元仿真能够排除外界红外辐射(视为噪声信号)对各点相位值的影响,因此仿真结果能够对激励频率的选择提供一定的理论指导。
已知的Q235钢材料的参数为:热导率49.8 W·m-1·K-1;比热容465 J·kg-1·K-1;密度7 840 kg·m-3。
通过有限元仿真,分别取得不同频率下缺陷中心处和非缺陷区的温度数据,经过傅里叶算法得到各缺陷中心对应的相位值,从而得到了如图4所示的2,6 mm预制深度的各缺陷尺寸下的相位差分布。
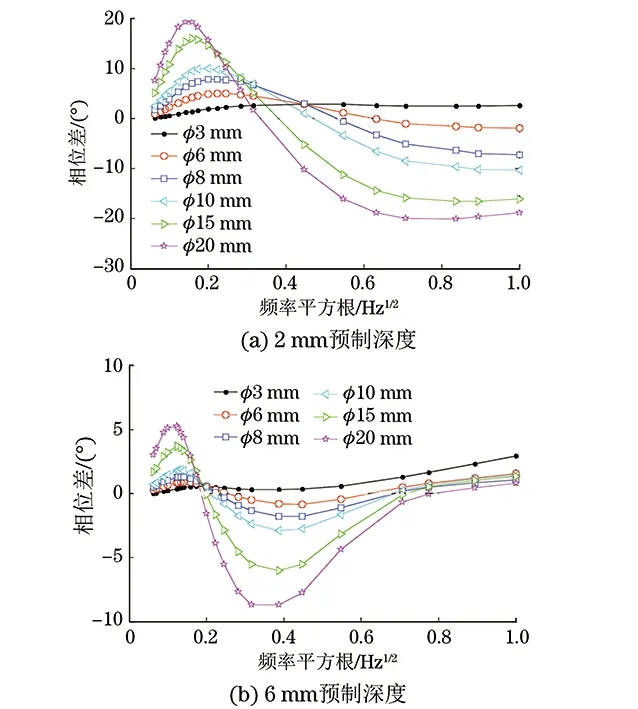
图4 不同预制深度下各缺陷的相位差-频率平方根曲线
由图4可知,在理想状态下,对于预制深度为2 mm的各平底孔缺陷,在锁相红外热像检测的常用检测频率范围内,其最佳频率在0.015~0.02 Hz之间;而对于深度为6 mm的各平底孔缺陷,其最佳频率同样也在0.015~0.02 Hz之间。故在检测试样中深度为2~6 mm的各平底孔缺陷时,选取0.015~0.02 Hz间的激励频率都将得到良好的锁相红外热像检测效果。
同时,由图4可知,对于预制深度为6 mm的各缺陷,在0.1 Hz左右的激励频率下存在着相位差的极大值,但该频率对于2 mm预制深度的各缺陷而言,相位差接近0°。而对于预制深度为2 mm的各尺寸缺陷,0.6~0.8 Hz范围内存在相位差的极大值,但该频率段下对于6 mm预制深度的各缺陷而言,其相位差同样接近0°。因此,“高频”激励不利于对试样内部不同深度缺陷同时进行检测。
4 缺陷定量分析
根据有限元仿真结果,得到了试样的最优激励频率范围。基于0.02 Hz激励频率下采集的红外温度数据,运用傅里叶算法,将各点相位值映射为灰度值后,得到如图5所示的相位图像,所识别到的缺陷的预制深度从上到下每排依次为2,4,6 mm。
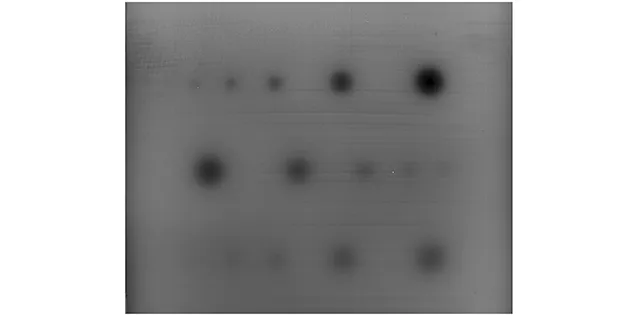
图5 试样相位图
由于采用了涂漆的方式来提高吸收率,因此在图5所示的相位图中存在着部分涂漆的痕迹。不仅如此,相位图还包含着外界噪声的信息。
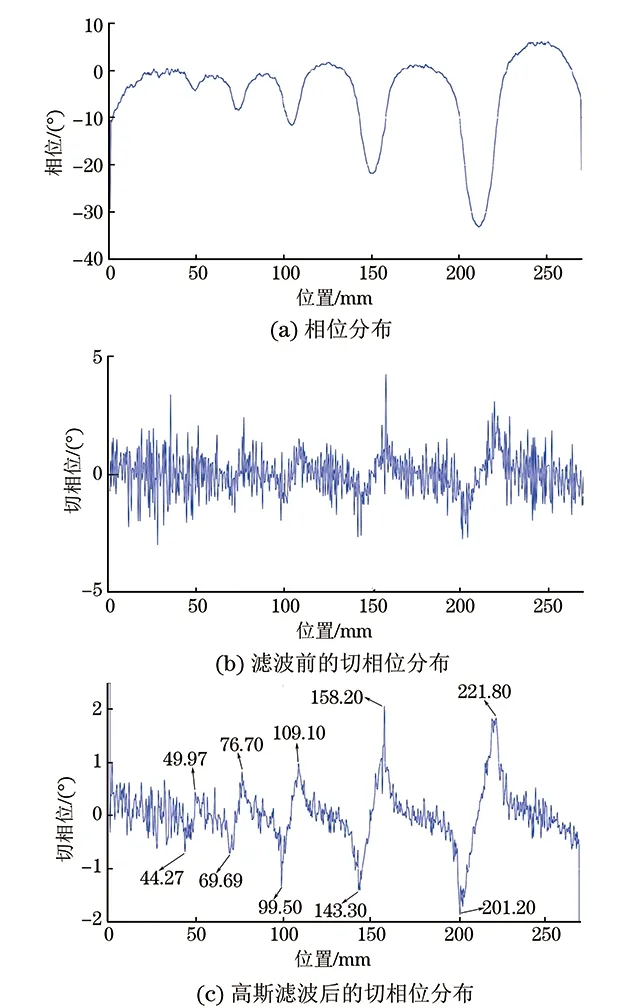
图6 2 mm预制深度的缺陷中心点连线处的相位分布及高斯滤波前后的切相位分布
4.1 切相位法
图6(a)为在0.02 Hz激励频率下2 mm预制深度的各缺陷中心点连线上的相位分布,仅仅通过图6(a)很难去检测缺陷的尺寸。图6(b)为对相位图上2 mm深度缺陷中心点连线上的各点所对应的相位值取一阶微分后的切相位分布,可以看到噪声信号对切相位法存在着相当强烈的干扰。因此在实际检测过程中,为了避免这些噪声信号的影响,需要在使用切相位法定量之前对相位图进行平滑处理。对相位图高斯滤波后,2 mm深度的缺陷中心点连线上的切相位分布如图6(c)所示。
试验与实践证明,若缺陷与非缺陷之间相位差在4°以内,运用切相位法无法实现缺陷尺寸的定量[5]。因此从右至左可检测出的2 mm预制深度的缺陷分别为A1、B1、C1、D1、E1,可以得到如表1所示的缺陷尺寸定量结果。
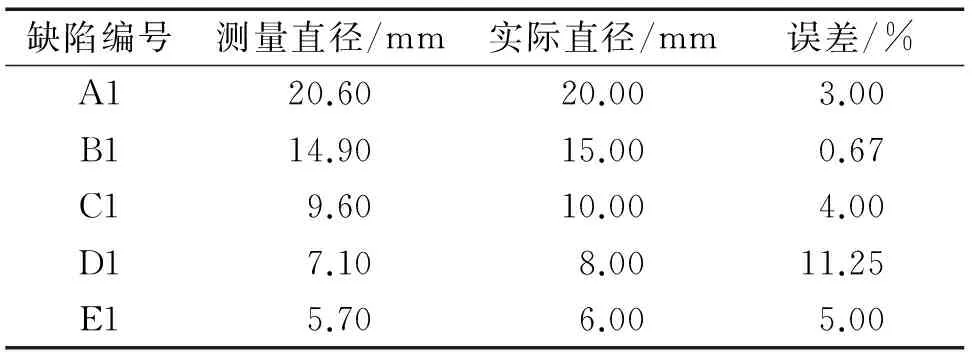
表1 切相位法对2 mm预制深度缺陷的定量结果
根据上述同样的步骤,可得到预制深度4,6 mm的各缺陷的定量结果,利用切相位法可定量的缺陷编号分别为A2、B2、C2、D2、A3、B3、C3,测量结果如表2所示。
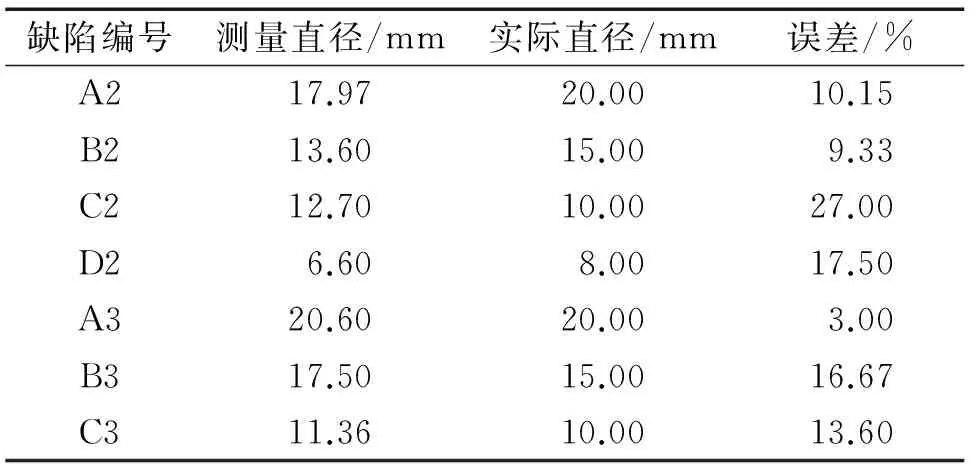
表2 切相位法对深度4 mm和6 mm缺陷的定量检测结果
试验结果表明,受外界噪声信号的影响,切相位法定量的结果并不是十分理想;并且由于平滑处理的影响,部分缺陷特征处因相位差变小而无法利用切相位法来定量。
4.2 区域划分下的FCM-边缘检测算子联合处理方法 从相位图中取出缺陷特征所在区域内的灰度值数据,作为样本集合,然后对每一个样本集合使用FCM聚类算法。相位图划分区域如图7所示,取相位图中能识别的缺陷特征A1、B1、C1、D1、E1、A2、B2、C2、D2、A3、B3、C3所在区域,分别定义为SA1、SB1、SC1、SD1、SE1、SA2、SB2、SC2、SD2、SA3、SB3、SC3。

图7 相位图划分区域
根据上述的 FCM理论,可知运用FCM算法时首先需要确定多个参数,其中最主要的包括模糊加权指数m、聚类数目c和阈值ε。
对于阈值ε,其值越小,迭代的次数会增加,聚类的效果越好。因此文章设置阈值ε为0.000 1。
模糊加权指数m是影响聚类结果的重要参数。相关文献中的试验结果表明,m值设为2时能得到相对最好的聚类结果[15-16]。
关于聚类数目c,刘俊岩教授等在文献[8]中提出对每个区域取聚类数目c=2,因此对每个区域使用FCM算法后样本集合都被分为两类。而在实际应用中,聚类数目设置为2时通常并不能得到最好的聚类效果。对此文章在每个区域的聚类数目c的设置上进行了改良。对于每个样本集合而言,聚类数目c的选择属于聚类有效性的问题。针对经典FCM算法,已提出了许多聚类有效性评价指标,其中XIE等[17]提出的VXB指数具有很高的使用率和优异性能,因此文章采用VXB指数来选择每个缺陷图像区域的聚类数目c。VXB指数计算如下:
由式(9)可看出,VXB指数是一个将数据集合的结构考虑在内的聚类有效性指数,分子表示类内的内聚程度,分母表示不同类之间的隔离程度。类间越离散,类内越紧致,说明聚类结果越好,因此最小的VXB指数对应着最优的聚类结果。因此最优聚类数目c*为:
获取每个区域所对应的相位图数据,设聚类数目c选择范围为[2,6],分别计算每个区域对应的VXB指数。VXB指数的值与聚类数目c和所选取区域的样本集合数据有关。这里不讨论区域选取时区域大小、位置的不同对VXB指数的影响;区域的选取遵循上文所提及的规则,对下文图9(FCM-边缘检测算子联合处理所得的特征图像)中选取的区域进行相关VXB指数计算,最终得到最优的聚类数目c*,如表3所示。
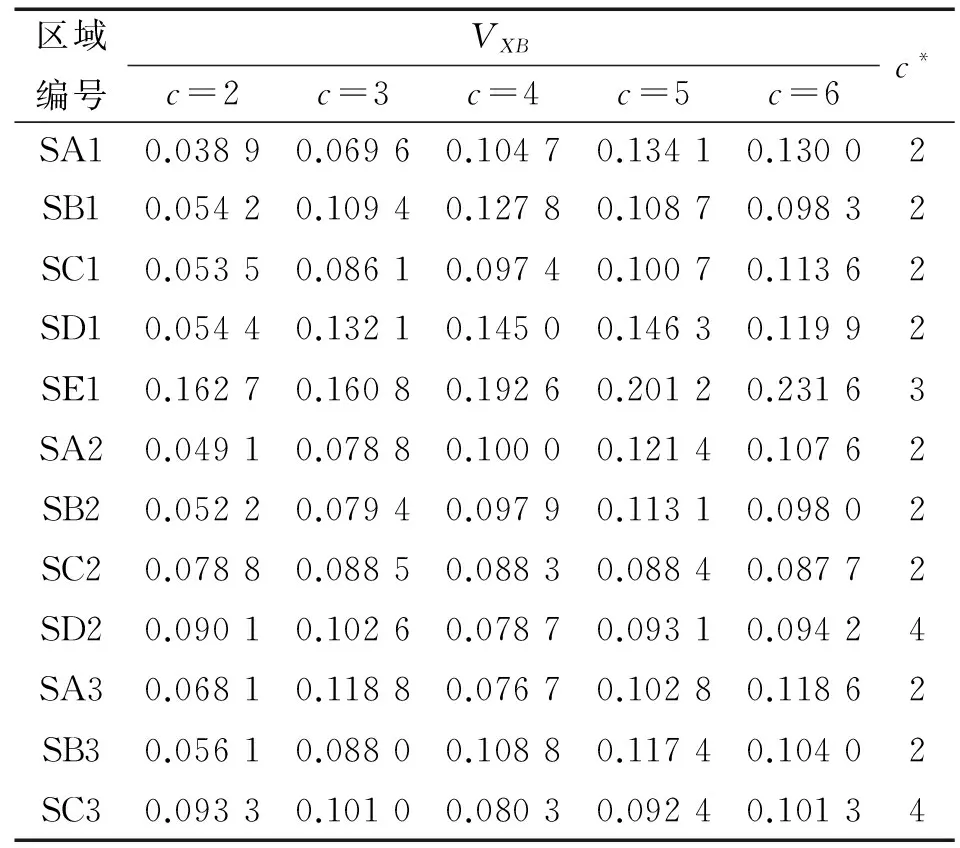
表3 不同区域下的VXB指数及最佳聚类数目c*
由表3的结果可知,每个区域的FCM算法的最优聚类数目c*都已确定。根据FCM算法原理,对某区域对应的总数为n的样本数据,算法得到的隶属矩阵U是一个n×c*的矩阵,因此U包含着c*个聚类结果。根据式(11),缺陷特征所对应的目标样本点k的所属类别Ck应满足在该类别下,隶属度值为最大值的条件:
最终,以Ck类的隶属矩阵来表述FCM算法处理后的区域内的缺陷特征信息。
图8是针对锁相红外检测的FCM-边缘检测算子联合处理方法的流程。
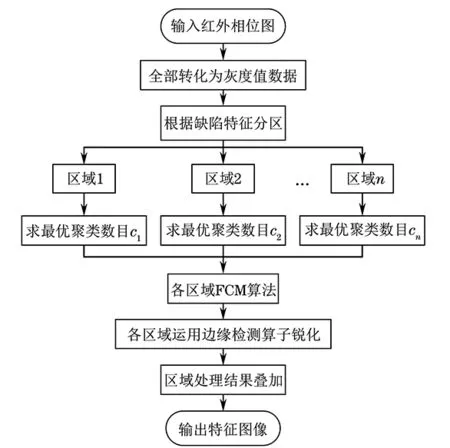
图8 锁相红外FCM-边缘检测算子联合处理方法的流程
根据上述流程,输入图5所示的相位图数据。Canny算子具有优异的性能,而被广泛使用于锐化处理中,因此文章采用Canny算子进行区域内部的锐化,最终得到如图9所示的存在缺陷特征的图像(文中简称“特征图像”)。
由图9所示,部分区域的处理结果仍会保留除缺陷特征以外的信息。尽管如此,从图9所示的特征图像中均能够提取出较完整的缺陷边缘。每个缺陷特征的边缘几乎都形成了封闭的、近似于圆的图形;通过这些封闭图形,可以对每个缺陷进行尺寸定量分析。

图9 FCM-边缘检测算子联合处理所得的特征图像
为了与切相位方法进行对比,根据图9所示的特征图像中过缺陷中心的水平位置上的缺陷特征边缘信息,通过式(12)计算各缺陷水平方向上的尺寸大小d。
式中:pL为特征图像中整个试样在水平方向上的像素点个数;pd为水平方向上的缺陷边缘间的像素点个数;L为所对应的试样在水平方向上的尺寸。
已知特征图像pL=616 mm,L=270 mm,由此得到了如表4所示的缺陷在水平方向上的定量结果,并与切相位法定量结果作比较。表中,d*表示平底孔缺陷实际直径大小,“-”表示在水平方向上无法定量。
在FCM-边缘检测算子联合处理方法所得的特征图像中,只有编号C2缺陷在过中心处的水平位置上缺失了边缘信息,因此无法在水平方向上进行定量。同样可以看到,切相位法对该缺陷的定量误差高达27%,引起误差过大的原因主要是该区域涂漆不均,使该缺陷特征失去了被定量分析的能力,因此在对比两种方法的缺陷定量效果时应将该缺陷C2排除在外。
而由表4可见,在水平方向上,其他缺陷通过区域划分下的FCM-边缘检测算子联合处理后得到了与切相位法定量结果相当、甚至更好的定量结果。对于试样中的大部分缺陷,得到了误差在10%以内的缺陷定量结果,证明了FCM-边缘检测算子联合处理方法的有效性。
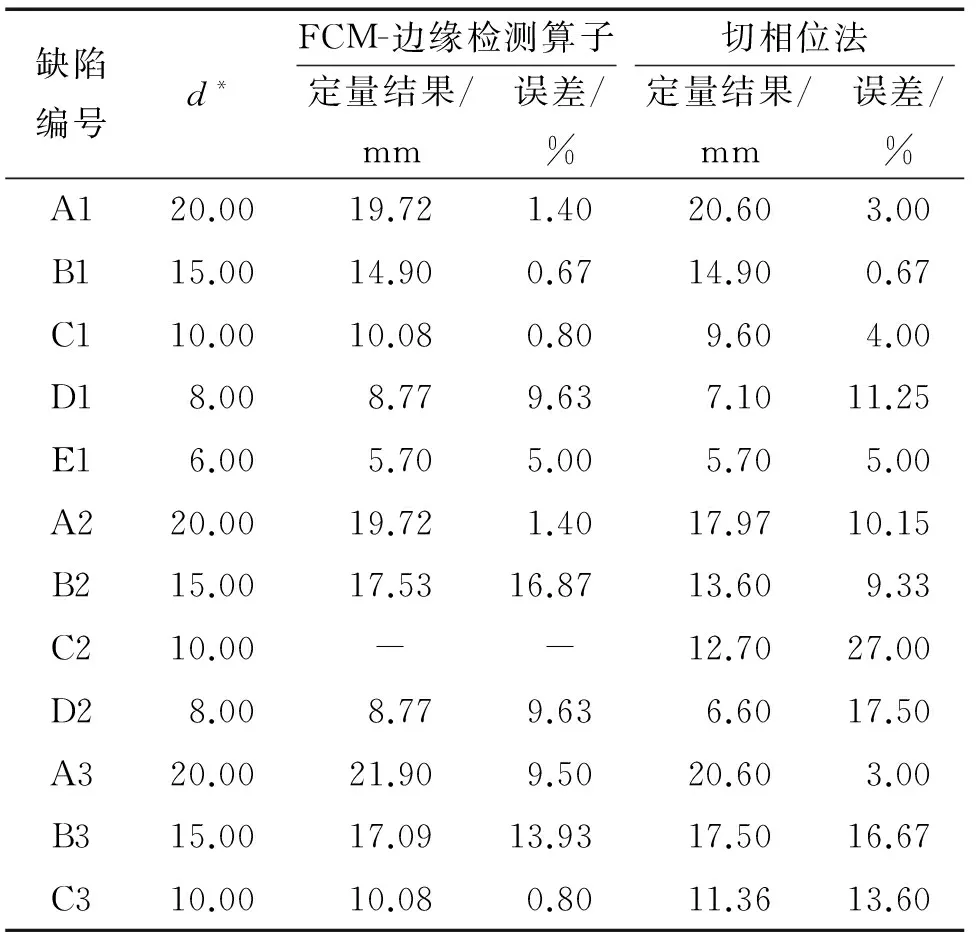
表4 FCM-边缘检测算子方法与切相位法的缺陷尺寸定量结果与对比
相较切相位方法, FCM-边缘检测联合处理方法有以下两个明显的优势:
(1) 能够得到直观的特征图像,通过合适的方法,能够实现缺陷特征面积的定量。
(2) 由聚类算法原理,该方法更适合于对不规则形状缺陷的尺寸定量。
5 结论
(1) 采用有限元方法得到了试样在锁相红外检测时的最佳激励频率的选择方案,并证明了使用较高激励频率时,检测存在着局限性。
(2) 在存在外界红外辐射干扰和检测方法本身造成的影响下,对于试样中的大部分缺陷,区域划分下的FCM-边缘检测算子联合处理方法能够得到误差在10%以内的缺陷定量结果。
(3) 与切相位法相比,FCM-边缘检测算子联合处理方法的定量结果更加直观,特征图像能够反映更多的缺陷边缘信息。因此该方法在锁相红外检测领域具有良好的应用前景。
[1] 王迅, 金万平, 张存林, 等. 红外热波无损检测技术及其进展[J]. 无损检测, 2004, 26(10): 497-501.
[2] 寇蔚, 孙丰瑞, 杨立. 正弦规律加热条件下缺陷红外故障响应[J] . 红外与激光工程, 2007, 34(4): 472-474.
[3] CHOI M, KANG K, PARK J, et al. Quantitative determination of a subsurface defect of reference specimen by lock-in infrared thermography[J]. Ndt & E International, 2008, 41(2): 119-124.
[4] MONTANINI R. Quantitative determination of subsurface defects in a reference specimen made of Plexiglas by means of lock-in and pulse phase infrared thermography[J]. Infrared Physics & Technology, 2010, 53(5): 363-371.
[5] CHAKI S, MARICAL P, PANIER S, et al. Interfacial defects detection in plasma-sprayed ceramic coating components using two stimulated infrared thermography techniques[J]. Ndt & E International, 2011, 44(6): 519-522.
[6] ZHOU Z G, ZHAO H X, SUN G K, et al. Inspection of disbonds in multilayer dissimilar metal structure using lock-in thermography[J]. Applied Optics, 2016, 55(16): 4490-4496.
[7] JUNYAN L, QINGJU T, XUN L, et al. Research on the quantitative analysis of subsurface defects for non-destructive testing by lock-in thermography[J]. NDT & E International, 2012, 45(1): 104-110.
[8] JUNYAN L, QINGJU T, YANG W, et al. Defects′ geometric feature recognition based on infrared image edge detection[J]. Infrared Physics & Technology, 2014, 67: 387-390.
[9] GUOFENG J, WEI Z, ZHENGWEI Y, et al. Image segmentation of thermal waving inspection based on particle swarm optimization fuzzy clustering algorithm[J]. Measurement Science Review, 2012, 12(6): 296-301.
[10] CHIWU B, QINGJU T, JUNYAN L, et al. Inspection on CFRP sheet with subsurface defects using pulsed thermographic technique[J]. Infrared Physics & Technology, 2014, 65(7):117-121.
[11] BUSSE G, WU D, KARPEN W. Thermal wave imaging with phase sensitive modulated thermography [J]. Journal of Applied Physics, 1992, 71(8): 3962-3965.
[12] BAI W, WONG B S. Evaluation of defects in composite plates under convective environments using lock-in thermography[J]. Measurement Science and Technology, 2001, 12(2): 142-150.
[13] 关庆, 邓赵红, 王士同. 改进的模糊 C-均值聚类算法[J]. 计算机工程与应用, 2011, 47(10): 27-29.
[14] IBARRA-CASTANEDO C, GONZALEZ D, et al.Infrared image processing and data analysis[J]. Infrared Physics & Technology,2004,46(1):75-83.
[15] WANG X, WANG Y, WANG L. Improving fuzzy c-means clustering based on feature-weight learning[J]. Pattern Recognition Letters,2004,25(10):1123-1132.
[16] JING L, DENG D, YU J. Weighting exponent selection of fuzzy C-means via jacobian matrix[C]//International Conference on Knowledge Science, Engineering and Management. Sibiu:Springer, 2014: 115-126.
[17] XIE X L, BENI G. A validity measure for fuzzy clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847.
A Defect Quantification Method by Lock-in Thermography
LI Gen1, ZHAO Hanxue1, FAN Jin1, ZHOU Zhenggan1,2
(1.School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics,Beijing 100083, China;2.The Collaborative Innovation Center for Advanced Aero-Engine (CICAAE), Beijing 100083, China)
To satisfy the requirement for defect quantification by lock-in thermography, a defect quantification method based on fuzzy C-means (FCM) and edge detectors was proposed. A finite element simulation model for the lock-in thermography inspection of prefabricated flat-bottom hole was built to find out the optimal modulated frequency. Experiments conducted on the specimen using lock-in thermography testing system with the optimal modulated frequency show that most of quantitative results of FCM-edge detector method with region division are better than that of the shearing-phase method, which is widely applied in lock-in thermography. The image processed by FCM-edge detector method contains much more information about defect edge than results got by shearing-phase method. Therefore, through appropriate image processing methods, area quantification is able to be achieved with FCM-edge detector method. The research results show that FCM-edge detector method with region division has good prospects in quantitative determination of defect by lock-in infrared thermography.
lock-in thermography; quantification method of defect size; the optimal modulated frequency; FCM-edge detector method with region division; shearing-phase method
2016-09-02
北京航空航天大学基本科研业务费资助项目(50100002015107039)
李 根(1992-),男,硕士研究生,主要研究方向为锁相红外热像检测技术
周正干,男,博士,教授,博士生导师,主要研究方向为超声及红外无损检测,zzhenggan@buaa.edu.cn
10.11973/wsjc201706001
V221+.3;TB553; TG115.28
A
1000-6656(2017)06-0001-07
