基于蒙特卡洛算法的新疆叶尔羌河上游流域地下水动态预测

古力皮亚·沙塔尔

(新疆喀什水文勘测局，新疆 喀什 844000)



基于蒙特卡洛算法的新疆叶尔羌河上游流域地下水动态预测

古力皮亚·沙塔尔

(新疆喀什水文勘测局，新疆 喀什 844000)

结合蒙特卡洛算法对新疆叶尔羌河上游某小流域地下水动态进行预测。研究结果表明：蒙特卡洛算法可考虑地下水变化的非平稳特点，对地下水的动态变化进行预测，预测值和地下水监测值之间的年和月尺度误差相对值均小于12%，相关系数分别达到0.71和0.85，蒙特卡洛算法在月尺度地下水预测精度好于年尺度预测精度。研究成果对于新疆区域地下水动态预测提供方法参考。

蒙特卡洛算法；地下水动态预测；预测精度分析；新疆叶尔羌河上游流域

新疆叶尔羌河流域地下水区域水资源的重要组成，对区域地下水变化趋势的动态预测可为区域地下水资源开发利用和保护提供重要依据。当前，国内许多学者展开过地下水动态预测的研究[1-5]， 但大都基于平稳时间数据系列进行预测，而地下水由于受人类活动和气象等综合因素的影响，其数据系列呈现非平稳的变化特征。近些年来，蒙特卡洛算法可对非平稳时间数据系列的变化趋势进行预测，在水资源领域得到具体应用[6-9]，但是在地下水预测研究还较少，特别是在新疆叶尔羌河流域还未进行具体应用，为此本文采用蒙特卡洛算法，对新疆叶尔羌河某小流域的地下水动态变化进行预测。

1 改进的蒙特卡洛算法原理

蒙特卡洛算法首先计算不同状态的失效概率，计算方程为：

(1)

在确定不同状态变量的失效概率后，需要各变量参数风险值进行计算，计算方程为：

(2)

其中在方程(2)中V(F)表示为参数风险值；S表示为计算仿真状态变量参数；X表示为随机状态变量；E(F)表示为均方差值。

在参数风险值确定后，需要对算法的收敛精度进行判定分析，判定方程为：

(3)

其中在方程(3)中β表示为模型计算收敛均差系数；V[E(F)]表示为期望最小均差值，经变化得到判定方程为：

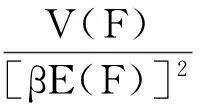
(4)

在方程(4)中在收敛精度确定的条件下，可以减少随机变量的抽样均方差来优化抽样次数，从而提高模型收敛计算精度。

本文引入交叉熵抽样方法对模型随机抽样进行优化和改进，从而提高模型收敛精度，交叉熵抽样方程为：

μ——表示基尼系数具体数据，在经济学与社会学领域，基尼系数受限于社会发展的局限性，取值范围在0-0.1的可能性很小，基尼系数的一般合理范围在0.1-0.3，鉴于医疗卫生资源配置过程中呈现的区域发展不平衡性，式中的阈值为0.2。也即是各地区医生数与医疗床位数针对地区人口与面积的基尼系数小于0.2，可以理解为资源分配相对公平。

(5)

其中在方程(5)中f(X，u)表示为随机变量概率密度分布函数；u表示为边缘密度概率函数；W(X，u)表示为无偏估计函数；g(X)表示为随机变量X的变动概率分布函数。

其中m的无偏估计计算方程为：

(6)

在确定抽样方法后，采用近密度函数对交叉熵抽样方程进行处理，处理方程为：

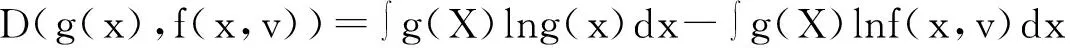
(7)

结合交叉熵抽样方式确定改进蒙特卡洛算法的最终方程：

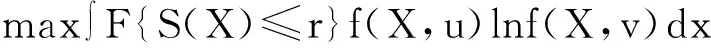
(8)

2 新疆叶尔羌河地下水动态预测

2.1 区域概况

本文以新疆叶尔羌河上游某小流域为研究区域，区域的集水面积为1 125 km2，研究区位于新疆南部喀什区域，为喀什地区较大的河流，流域地下水占总水资源的比例在20%～40%之间，区域多年平均降水量为60～80 mm，降水主要集中在夏季7～9月份，区域地下水补给主要为降水入渗补给，河床径流补给量相对较少，流域内有5处地下水位监测点，监测点的数据系列为1960～2015年。

2.2 参数估计

在模型应用时，首先需要对蒙特卡洛算法的参数m值进行无偏估计，本文采用极大熵谱法对参数进行无偏估计，确定模型参数的上限值和下限值。参数估计结果见表1。

2.3 预测精度分析

2.3.1 年尺度地下水动态预测

本文结合蒙特卡洛算法对区域地下水进行预测，其中1960-2004年共55年的地下水位监测数据作为模型训练计算样本，2005-2015年地下水位监测数据作为预测精度分析，年尺度精度分析结果见表2，相关性分析结果见图1(a)。

表1 模型参数无偏估计结果

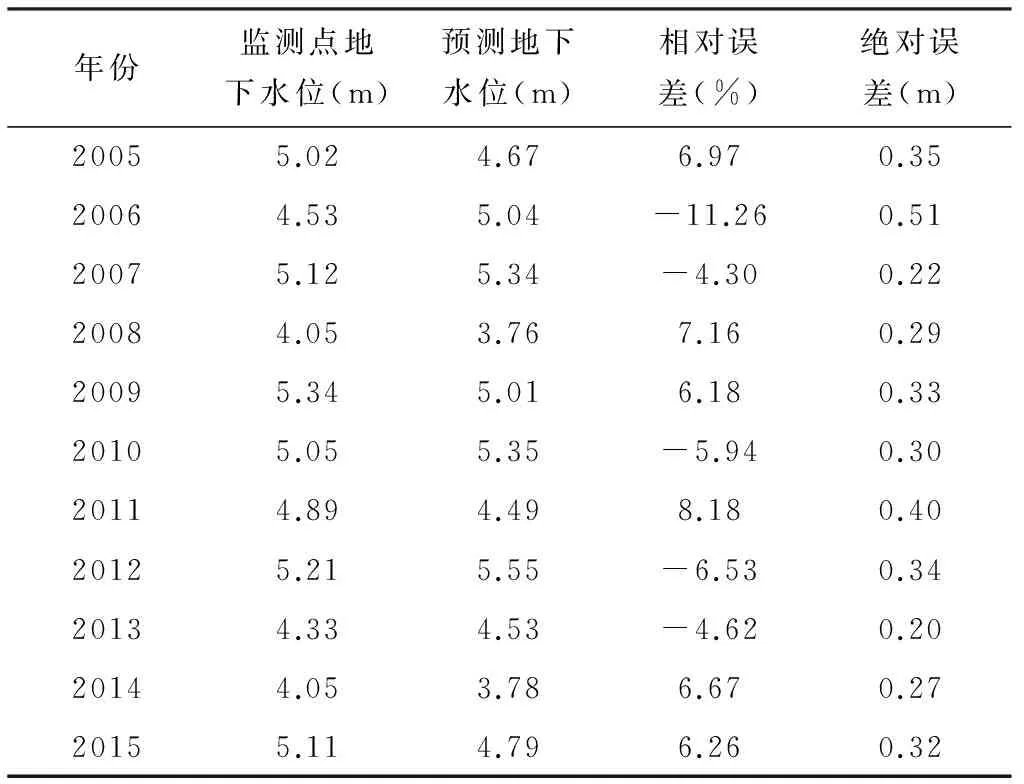
表2 基于蒙特卡洛算法的研究区年尺度地下水位预测精度分析

2.3.2 月尺度地下水动态预测

在年尺度预测精度分析的基础上，本文结合蒙特卡洛算法对区域地下水月尺度的精度进行分析， 月尺度精度分析结果见表3，相关性分析结果见图1(b)。

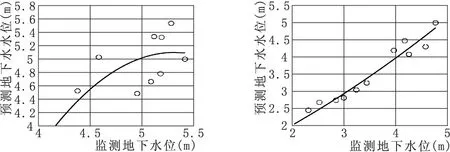
(a)年尺度 (b)月尺度

从表2中可以看出，蒙特卡洛算法在年尺度预测的地下水位和监测水位各年份误差小于12%，误差绝对值在0.22～0.51 m之间，计算效果较佳。月尺度预测地下水位和监测水位之间的误差相对值也均小于12%，绝对误差值在0.11～0.30 m之间，计算精度整体好于年尺度预测精度，这主要是年尺度预测存在平均值误差，使得预测精度低于月尺度。从图1中可以看出，年尺度和月尺度预测的地下水位和监测地下水位相关系数分别为0.71和0.85,属于高度正相关。可见，蒙特卡洛算法在新疆叶尔羌河上游流域动态预测精度较高。

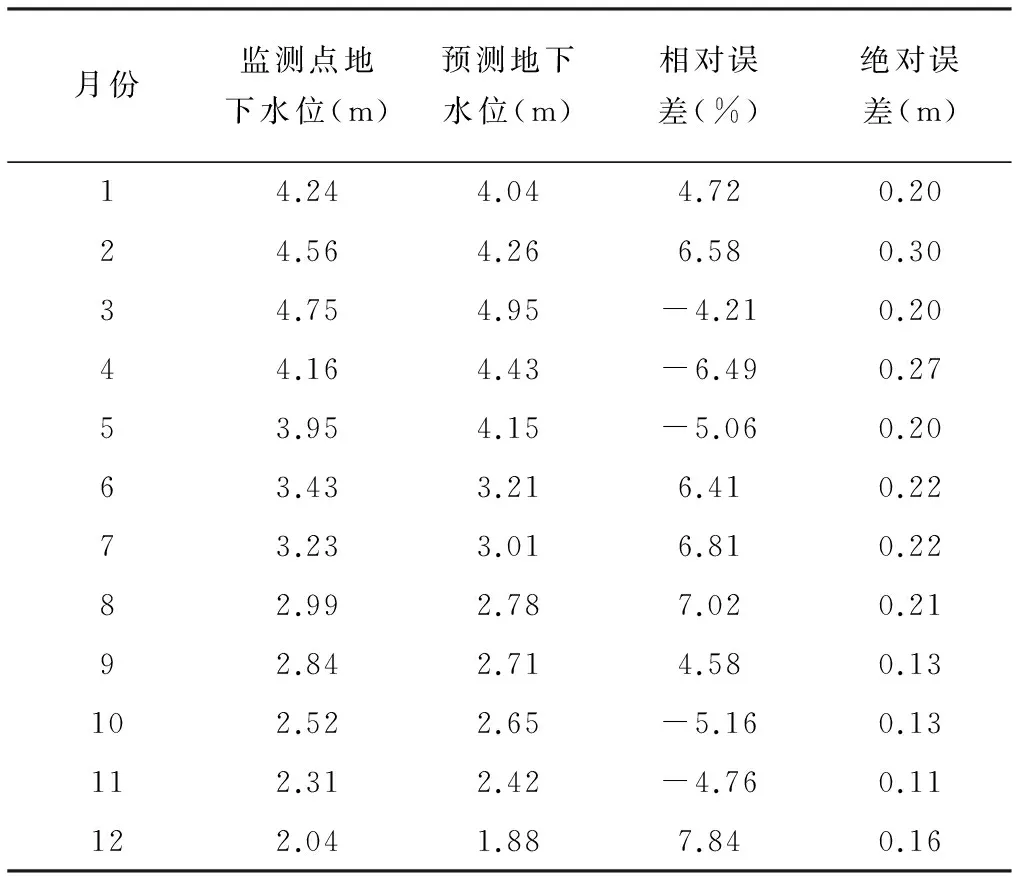
表3 基于蒙特卡洛算法的研究区月尺度地下水位预测精度分析

3 结语

蒙特卡洛算法可对非平稳时间数据系列的变化趋势进行预测，在水资源领域得到具体应用，但是在地下水预测研究还较少，特别是在新疆叶尔羌河流域还未进行具体应用，通过采用蒙特卡洛算法，对新疆叶尔羌河某小流域地下水动态变化进行预测，结果表明该算法适合区域地下水动态预测，月尺度地下水动态预测精度总体好于年尺度，对区域地下水变化趋势的动态预测可为区域地下水资源开发利用和保护提供重要依据。

[1]张海飞. 地下水动态预测模型概述[J].地下水.2016,(01):68-70.

[2]程银才,李明华. 灰色双向差分模型在地下水动态预测中的应用[J].地下水.2008,(01):9-11.

[3]王光生,杨建青,于钋,等.地下水动态预测的探讨[J].水文.2013,(03):25-28+51.

[4]李贺丽. 地下水动态预测方法分析[J].河南水利与南水北调.2011,(07):54-55.

[5]平建华,李升,钦丽娟,等.地下水动态预测模型的回顾与展望[J].水资源保护.2006,(04):11-15.

[6]张和喜,迟道才,王永涛,等.基于NNBR与蒙特卡洛算法的降雨量预报模型应用研究[J]. 水土保持研究.2014,(02):106-110.

[7]翟海涛,罗潋葱,李慧赟,等.蒙特卡洛算法在水动力水质模型(DYRESM-CAEDYM)参数优选中的应用[J].生态科学.2014,(01):38-45.

[8]韩京成,黄国和,李国强,等. 基于贝叶斯理论的SLURP水文模型参数不确定性评估及日径流模拟分析[J].水电能源科学.2013,(12):13-17.

[9]卫晓婧,熊立华,万民,等.融合马尔科夫链-蒙特卡洛算法的改进通用似然不确定性估计方法在流域水文模型中的应用[J].水利学报.2009,(04):464-473+480.

2016-12-19

古力皮亚·沙塔尔(1974-)，女，新疆喀什人，工程师，主要从事工程档案管理、水文分析计算方面的工作。

P641.74

B

1004-1184(2017)03-0210-02