基于原型观测试验的引水隧洞糙率反推计算及过水能力复核方法探讨

2017-06-19李辉

地下水 2017年3期

关键词：反推糙率恒定

李辉

(辽宁省铁岭水文局，辽宁铁岭 112000)

基于原型观测试验的引水隧洞糙率反推计算及过水能力复核方法探讨

李辉

(辽宁省铁岭水文局，辽宁铁岭 112000)

本文基于原型观测试验的方式并结合一维非恒流方程对辽宁中部某引水隧洞糙率进行反推计算，并结合糙率反推结果对引水隧洞过水能力进行复核方法进行了探讨。计算结果表明：原型观测试验结合一维非恒流方程的算法可实现引水隧洞糙率的反推计算，计算糙率结果较为合理，小于工程设计糙率值；经过水能力复核计算，引水隧洞现状过水能力可满足设计规范要求。研究成果对于引水隧洞糙率反推和过水能力复核提供方法参考。

原型观测方法；引水隧洞糙率反推；非恒定流方程；过水能力复核

引水隧洞是城市供水的重要工程措施，当前，城市水引水资源供需日益紧张，急需对引水隧洞的过水能力进行复核计算，若引水隧洞的过水能力已经达到城市供水需求，则不需要再建引水设施，减少工程投资。而复核后的引水隧洞过水能力已经不能达到城市供水需求，则需要再建或者扩建引水设施，从而达到城市供水的要求，因此对引水隧洞过水能力复核计算十分重要。对于引水隧洞过水能力的复核关键在于糙率的推求，对于引水隧洞糙率反推国内许多学者展开相关研究，并取得一定研究成果[1-6]。在这些成果中较为成功为采用原型观测试验的方法，结合实测水位流量数据，应用曼宁公式(均匀恒定流)反推隧洞糙率，但是引水隧洞由于来水受闸门启闭影响，呈现非恒定流流态，采用恒定流反推糙率存在计算误差，为此本文引入一维非恒定流方程[7-8]，以辽宁中部某引水隧洞为工程实例，基于原型观测试验方式对隧洞糙率进行反推，结合反推糙率对隧洞过水能力进行复核计算。

1 引水隧洞糙率反推及过水能力复核计算方法

引水隧洞水流受闸门启闭影响，水流呈现非恒定流流态，传统糙率反推方法采用基于恒定流方程的曼宁公式计算，存在计算缺陷，为此本文选用一维非恒定流方程来进行引水隧洞糙率的反推计算，通过试算不同水深下的糙率，模拟不同时刻断面的水位、流量，直到模拟的水位、流量与实测水位、流量较吻合(原型观测试验测定)，将试算最优结果的综合糙率作为隧洞反推的糙率。结合反推的糙率，结合不同来水量，计算断面过水能力，对引水隧洞过水能力进行复核。其中糙率作为参数进行输入，一维非恒定流得水位和流量计算方程为：

(1)

在方程(1)中Q表示断面流量，单位m3/s；Z表示断面水位，单位m；u表示为断面平均流速，单位m/s；A表示断面横断面面积，单位m2；x表示沿水流纵向的水平距离，单位m；t表示为计算时间，单位h；g表示为重力加速度，单位为m/s2；a表示为流速不均匀分布系数，无量纲；Sf表示为水力学坡降；B表示为断面宽度，单位m。

结合Preissman四点加权差分格式对方程(1)进行求解计算，在方程组中变量的导数差分格式见方程(2)：

(2)

在方程(2)中θ表示方程加权系数， f表示为推求断面水位值和流量值，单位分别为m和m3/s，其他变量含义同方程(1)。

2 工程实例分析

2.1 引水隧洞原型观测试验断面设置

研究的引水隧洞总的长度为3 000 m，隧洞过水能力要求为5 m3/s，才能满足城市现状供水需求。在原型观测试验中，设置5个断面，各试验断面间距为250 m，其中I、II 、II、VI、V断面均进行水位测定，II、III为流量测定断面，进行流量测定，各试验断面布设图见图1。

2.2 断面水位流量测定方法

2.2.1 流量测定

II、III断面安装流量计。结合隧洞形状，流量计安装在隧洞底板中部，蓄电池安装在隧洞顶部，中间连接电缆，电缆外部加护管保护。为防止隧洞内淤积对流量计的影响，流量计安装高度距地面8 cm，下部为U型不锈钢板。为防止漂浮物影响，U型不锈钢板采用加长处理，迎水侧进行封闭处理。

图1 原型观测试验断面布设图

2.2.2 水位测定

I、VI、V断面安装雷达水位计，考虑横比降的影响，水位计及蓄电池全部采用悬挂式，安装在隧洞顶部中间位置。水位计仪器箱底部距隧洞底板2.5 m，能够满足施测最大水深2.13 m的要求。

2.2.3 仪器参数设置

对水位计、流量计的参数进行设置。测量历时均为60 s，测量间隔5 min，每小时测量12次。各台仪器统一授时，以保证测验时间的同步性。

2.3 试验断面测量计算

试验断面测量是糙率反推的基础，对布设的5个试验横断面进行了测量，并对隧洞沿程纵断面进行了测量，断面测量结果见图2。

图2 隧洞测量成果示意图

2.4 原型观测试验测定结果

结合10组放水试验，进行原型观测试验，对断面的水位和流量进行试验测定，各断面水位流量试验测定结果见表1和表2。

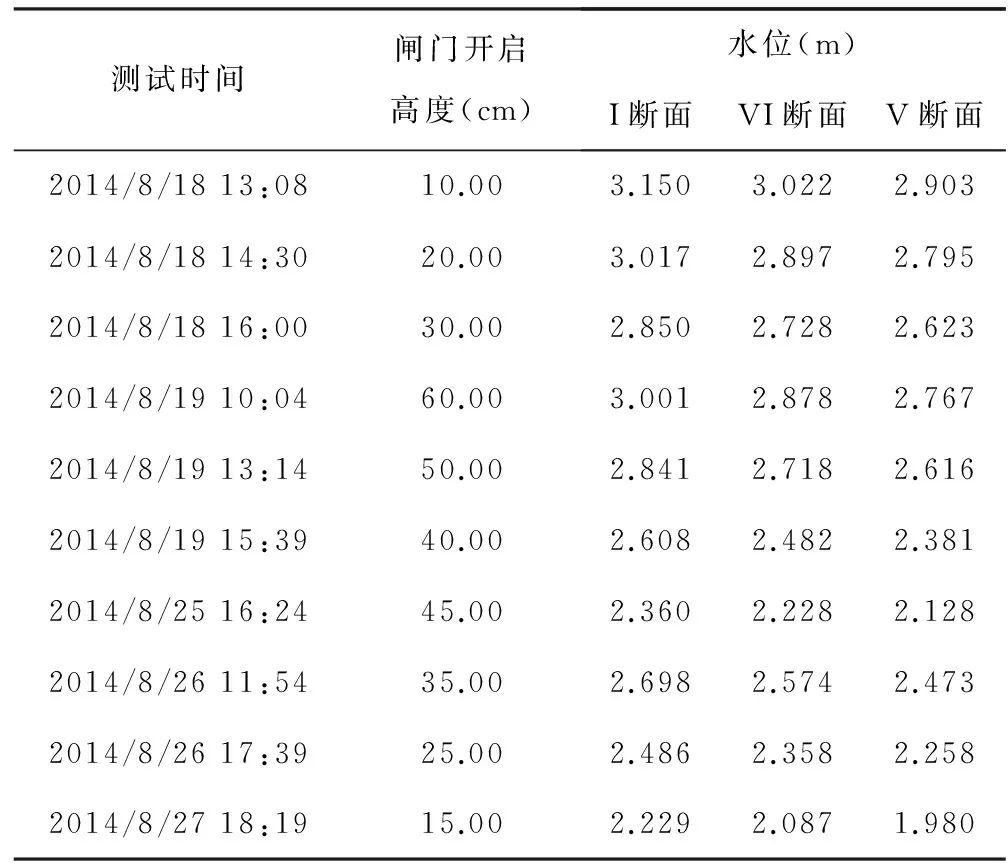
表1 原型观测试验断面水位测定结果

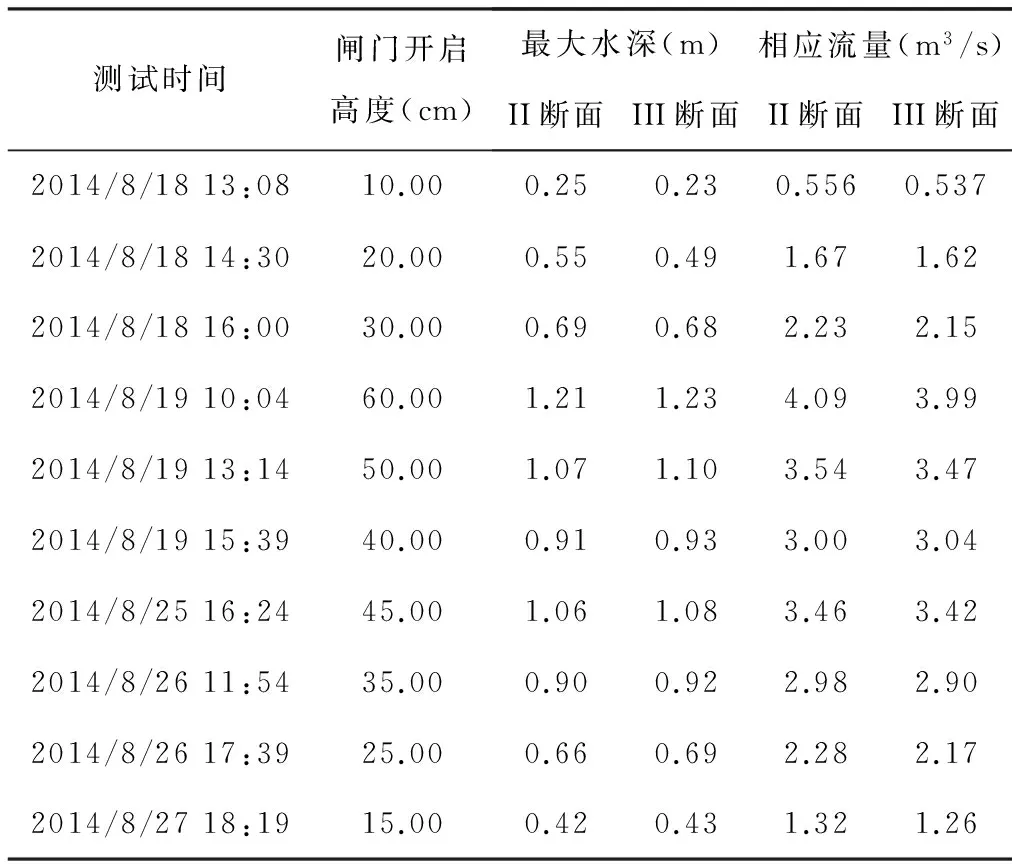
表2 原型观测试验断面流量测定结果

2.5 基于一维非恒定流模型糙率反推结果

将I断面和V断面水位作为模型上、下水位边界，通过糙率试算，推求III断面的流量，结合实测III断面数据，进行分析计算，当推求的流量和实测流量较为接近，当前模型糙率值即为糙率反推值。引水隧洞糙率反推结果见表3。

从表3中可以看出，经过糙率试算后，计算的流量和水深和原型观测试验断面流量和水深拟合度均较高，从表中可以看出，反推计算的糙率在0.013 6～0.019 4，在低水时，其糙率较低。在高水时，其糙率较。从和设计糙率对比结果可以看出，在不同水深下，反推的糙率均低于设计糙率值，这主要是在引水隧洞工程设计时，考虑到引水隧洞工程安全性，增大了不同水深下的设计糙率值。

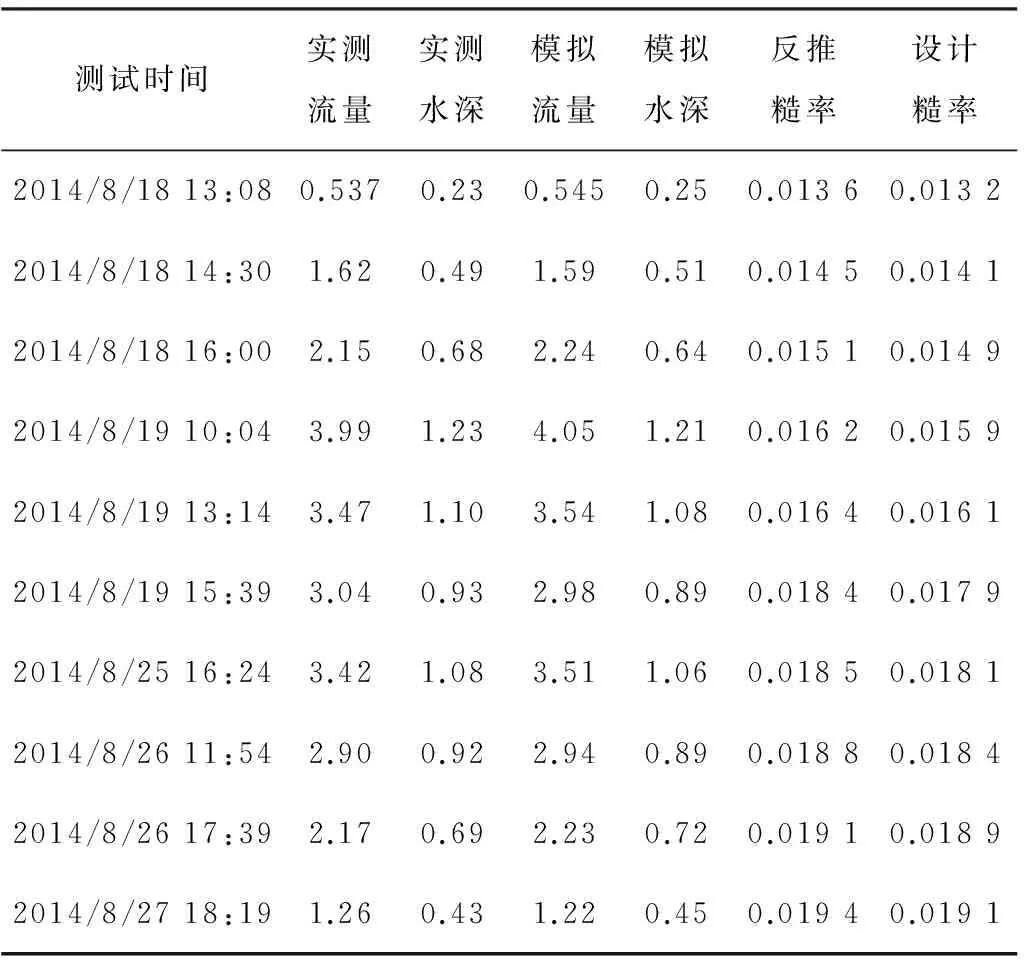
表3 基于一维非恒定流模型模拟成果

2.6 糙率合理性验证

为验证反推糙率的合理性，结合放水试验，对应选取III断面10个洪峰时刻流量，结合糙率反推结果，计算III断面不同水位下的流量值，对比试验测定的流量值，分析计算糙率反推结果的合理性，分析计算结果见表4和图3。

表4 糙率验证结果

图3 反推糙率验证结果

从表4中可以看出，采用反推计算的糙率计算的流量和实测流量之间的误差较小，计算误差在0.9%～-5.8%之间，符合水利工程设计规范要求。表明反推计算的引水隧洞糙率值较为合理。图3为基于反推糙率计算流量和实测流量的对比结果，从图中可以看出计算流量和实测流量过程较为吻合，相关性较高。综上表明结合原型观测试验的一维非恒定流的糙率反推计算方法在引水隧洞糙率反推计算中具有较好的适用性。

2.7 隧洞过流能力复核方法探讨

传统隧洞过水能力复核计算，结合隧洞出口断面流量测定数据，对过水能力复核计算，但是引水隧洞沿程水流由于糙率影响，均有损损失，因此传统方法推算的隧洞过水能力可能小于隧洞实际的过水能力，本文推荐采用隧洞糙率反推结果，通过设定隧洞最大水深，利用非恒定流方程推算隧洞最大的过水能力，使得隧洞过水能力计算更加合理化。以本文引水隧洞工程为例，在糙率反推结果的基础上，对引水隧洞的过水能力进行复核计算，结合一维非恒定流数学模型进行推算，当隧洞水深H=1.65 m时，可通过5.25 m3/s，引水隧洞径高为0.51 m，隧洞的净空为21.48%均可满足水利工程设计规范要求，隧洞内的流速为1.213 m3/s，满足其设计过水隧洞过水能力要求(要求过水能力在5 m3/s)。