初中数学逻辑思维能力培养刍议

邱春霖

【摘 要】数学是培养学生逻辑思维能力最好的载体。教师应重视在初中数学教学中培养学生逻辑思维能力和良好的逻辑思维品质。

【关键词】逻辑思维能力的培养；数学教学活动

逻辑思维能力是指正确、合理思考的能力。即对事物进行观察、比较、分析、综合、抽象、概括、判断、推理的能力，采用科学的逻辑方法，准确而有条理地表达自己思维过程的能力。而良好的逻辑思维品质应具有逻辑思维的灵活性、深刻性、独立性和创造性。 数学是用数量关系（包括空间形式）反映客观世界的一门学科。在数学教学活动中，任何一个概念的学习，一个问题的判断和分析，都离不开逻辑思维活动。可以说，学习过程中逻辑思维无处不在无时不有。因此，数学是培养学生逻辑思维能力最好的载体。

那么，应该如何培养数学逻辑思维能力呢？本人认为应该从以下几点着手。

一、在代数教学中培养逻辑思维能力

代数是研究数、数量关系及其性质的数学分支。初中学生入学时已具有一定的演算能力和思维能力，教学过程中，只要教师积极开发学生感兴趣的并且有能力获得结果的问题，学生一般都会积极主动地去思考。这样，在探究数量关系和推理过程中，逻辑思维能力自然而然得以培养和提升。

1.把逻辑思维训练嵌在不等式的学习中

不等式是表示数量不等关系的式子，其数量关系较为抽象，往往要将不等式的解集在数轴上表示出来，使数量关系直观化，也使思考问题的过程简单化。

例如，在学习一元一次不等式时，问“如果关于x的不等式x≤a有3个正整数解，那么a的取值范围是什么？”首先在数轴上表示不等式x≤a的解集（如下图），使之包含3个正整数1、2、3，初步确定a介于3和4之间，其次，因为解集中含有等号，a的取值范围包含3而不包含4，所以a的取值范围是3≤a<4。

如上所述，要想明晰一个问题的解题思路，需要教师积极地引导学生进行观察、比较、判断等基本的逻辑思维活动，而在这一系列的思维活动中，教师已把逻辑思维训练悄无声息地嵌入其间。

2.在方程及其应用的学习中培养逻辑思维能力

数学来自于生活而又为生活和生产实践活动服务，生活中，常用来解决现实问题的是数学方程。在研究方程的应用时，寻找等量关系是解决问题的关键。在求解过程中，需要不断地运用到人脑的逻辑思维。毋庸置疑，应用题的求解过程是提升学生逻辑思维的最佳契机。

例如，林老师为了在班级里开展小组合作学习，欲将本班45名学生分成若干个小组，每组分成5人或6人，问：有几种分组方案？若假设5人的分x组，6人的分y组，则5x+6y=45，所以x=（45-6y）÷5，因为x、y的实际意义是正整数，所以45-6y必须能被5整除，当y=5时x=3，所以，只有一种分组方案，也就是5人的分3组，6人的分5组。

以上的教学活动，教师在引导学生寻求解题方法的过程，就是带领学生积极进行观察、比较、判断、分析、综合等逻辑思维活动的过程。观察中找到问题的根源；比较里明晰问题的差别；判断时获得解决问题的路径；分析综合中找到了解决问题的最佳方案。在这些活动过程中，学生的思维能力得到了很好的训练及提升。

二、在几何教学中培养逻辑思维能力

初中几何是数学学科中几何分支的入门阶段，其主要目的是培养学生空间想象能力、逻辑思维能力和推理能力。因此，我们应该重视学生在几何课程学习中逻辑思维能力的训练和培养。

1.逐步对学生进行逻辑语言能力训练

逻辑语言是逻辑思维的表现形式，任何逻辑思维都离不开前因后果的逻辑推理。例如在几何入门阶段学习线段时，如果点O是线段AB的中点，那么就有AO=BO或AB=2AO=2BO或AO=BO=0.5AB这些数量关系，如何选用这些来进行推理演算，这与题目的已知条件和所求的结论有关系，但都离不开“因为……所以……”的逻辑形式。逻辑推理的表达是初一学生从前没有接触过的新生事物，教师应该规范演示，再让学生模仿训练，从一步推理开始，再逐渐增加推理步数，循序渐进，同时要求学生加注推理的理由，为后续学习逻辑推理打下良好的语言表达基础。

2.重視培养多角度分类逻辑思维能力

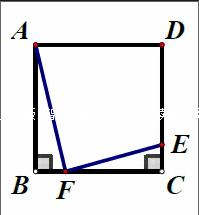
学习几何离不开研究图形的形状、位置和大小。思考问题时，经常出现图形位置的上下之分、左右之分、内外之分与顺序之分等问题，在观察角度不同的情况下往往会得出截然不同的结论，教学中应重视引导学生进行多角度分类逻辑思维，考虑问题要周全。在函数问题中也经常会出现需要分类来考虑问题的情况，或因坐标的符号不同或因点所在的位置不同而产生相异结论。如图，在边长为8的正方形ABCD中，点E、F分别在CD和BC边上，CE=1，连接AF和EF，当BF为多少时，△ABF与△ECF相似？在这个问题中，两个三角形的两条直角边成比例的顺序不同，BF就有两个不同的结果。我们要善于开发和利用这样的教学素材，重视培养和提高学生的分类思考问题的逻辑思维能力。

3.重视培养多方向逻辑思维能力

培养逻辑思维能力，既要让学生认识逻辑思维方向的科学性，还要指导学生积极进行多向性逻辑思维。首先要精心设计训练内容，好题目对学生的训练可以起到四两拨千斤的作用。其次，依据数学基础知识所包括的概念、公式、定义、定理和法则等，讲究正确的思维方向。再者，不要满足于已得到的解题方法，多问问自己，有没有其它更加巧妙和简洁的解题途径，引导学生从不同的方向去思考问题。经过积极的反复的多向思维训练，才能避免学生产生思维定式，保持逻辑思维的活跃性。如图，在矩形ABCD中，AD=30，AB=20，E为AB的中点，点F在BC上，且BF=2FC，AF分别交 DE、DB于点M、N，求MN的长。如图①、图②、图③就是从线段的端点或分点不同的方向来构建相似三角形，利用相似三角形对应边成比例的性质求解，而得到不同的解题方法。

教学中，数学教师通过教导学生注意前后知识之间的联系，使新旧知识得以贯穿运用。对于教材里的能力提升题，教师应该放手让学生自己去思考，独立完成，教师只要从逻辑思维的方向和逻辑思维的角度给予指点，并对学生的解题方法进行点评，鼓励学生积极思考，积极进行习题的重构，寻求尽量多的和尽量好的解题方法。这样，既巩固和加深了知识点的理解又让学生的逻辑思维能力得到发展，也培养了学生独立性逻辑思维和创造性逻辑思维的良好品质。

总之，在初中数学教学中，教师必须要讲究教学方法，重视培养学生的逻辑思维能力和良好的逻辑思维品质。在课堂教学中必须转变观念，少一些灌输多一些引导和启发，让学生的逻辑思维能力得到不断发展，多为国家经济建设培养高素质的人才。

参考文献：

[1]王志军.《新一代月刊》.培养学生思维能力推进高效课堂建设——浅议初中数学课堂应注意的问题，2012（2）.

[2]张文胜.《读与写旬刊》.浅谈新课程下初中学生数学创新思维能力的培养，2016（13）.

[3]周文亭.《新课程：下》.浅谈初中数学教学中对学生创新思维能力的培养策略.