基于Allan方差的MEMS陀螺仪随机误差分析方法

蒋孝勇， 张晓峰， 李孟委

(1. 中北大学 电子测试技术国家级重点实验室， 山西 太原 030051；2. 中北大学 仪器与电子学院， 山西 太原 030051)

基于Allan方差的MEMS陀螺仪随机误差分析方法

蒋孝勇1,2， 张晓峰1， 李孟委1,2

(1. 中北大学 电子测试技术国家级重点实验室， 山西 太原 030051；2. 中北大学 仪器与电子学院， 山西 太原 030051)

MEMS陀螺随机漂移误差是制约惯性导航精度的主要原因， 本文通过Allan方差分析方法， 得出MEMS陀螺随机漂移误差主要来源以及各种误差的性能参数. 该方法为分析陀螺性能指标、 提高惯性导航精度奠定了基础. 本文介绍了Allan方差定义， 陀螺各项随机误差与Allan方差的关系， 搭建了MEMS陀螺组件， 通过高精度转台实验静止采集陀螺仪数据. 利用Allan方差分析得出MEMS陀螺各项随机误差性能指标， 验证了该方法的可行性.

MEMS陀螺仪； Allan方差； 陀螺随机漂移； 零偏不稳定性

0 引 言

MEMS惯性器件具有体积小、 成本低、 方便集成等优点， 随着其精度的日益提升， 未来将大批量装备战术级惯导系统， 发展前景广阔[1,2]. MEMS陀螺随机漂移误差是制约MEMS陀螺性能的关键因素. 对MEMS陀螺随机漂移误差分析不仅能找到随机漂移的误差来源， 为MEMS前期器件设计加工提供依据， 而且能通过分析得出误差参数， 建立误差补偿模型， 提高MEMS陀螺的工程使用精度. 目前分析MEMS陀螺随机漂移性能指标的方法有1σ标准差和Allan方差两种[3-5]. 1σ标准差方法简单， 能够反映出MEMS陀螺随机漂移趋势和漂移指标， 能够反映出陀螺平均意义上的零偏稳定性. 但1σ标准差不能详细地给出各种误差来源和各误差源具体指标参数[6,7].

1 Allan方差定义

以τ0为采样周期对MEMS陀螺输出角速率ω进行采样， 得到有限个数据点N. 将N个数据点平均分成K组， 每组M个数据点， 要求M≤(N-1)/2， 则有K=N/M. 数据分组情况如图 1 所示.

根据上式可知各组均值为

(1)

则Allan方差可用

(2)

图 1 数据分组情况示意图Fig.1 Schematic diagram of data grouping

2 各项噪声源及其Allan方差

通过Allan方差可以很直观地反映MEMS陀螺的性能水平. 在此之前需要建立MEMS陀螺各种误差源与Allan方差之间的对应关系. MEMS陀螺随机漂移误差源一般包括： 零偏不稳定性、 量化噪声、 角度随机游走、 角速率随机游走、 速率斜坡. 本文通过各种误差源的功率谱建立误差源与Allan方差之间的关系. 详细的推导过程如下所述.

2.1 量化噪声(Quantization Noise， QN)

量化噪声是一切量化操作所固有的噪声， 只要进行数字量化编码采样， 传感器输出的理想值与量化值之间就必然存在微小的误差. 对于“四舍五入”型量化噪声， 常常视其为服从均匀分布的零均值白噪声且易知其方差为Δ2/12， 该噪声功率谱在f=-fs/2～fs/2上为常数(其中fs=1/τ0)， 根据信号时频方差跟频域功率谱积分面积相等原则， 得角度量化噪声的功率谱密度

(3)

(4)

将式(4)带入Allan方差频域到时域转换式(5)

(5)

可得

(6)

图 2 Allan方差的τ～σRR(τ)双对数曲线Fig.2 Allan variance sigma τ～σRR(τ) double logarithmic curve

2.2 角度随机游走(Angular Random Walk, ARW)

角度随机游走是一种独立增量过程， 对于陀螺角度随机游走而言， 独立增量的含义是： 角速率白噪声在两相邻采样时刻进行积分， 不同时间段的积分值之间互不相关. 从角速率方面看， 角度随机游走功率谱可看做常数， 又Sω(f)=N2， 式中N为角度随机游走系数， 将该式带入式(5)可得

(7)

2.3 零偏不稳定性噪声(BiasInstability，BI)

零偏不稳定性噪声通常也被称为1/f噪声， 其功率谱密度与频率成反比， 又零偏不稳定性噪声的角速率功率谱为Sω(f)=B2/(2πf)(式中B为零偏不稳定性系数)， 将该式带入式(5)中， 可得

(8)

2.4 角速率随机游走(RateRandomWalk，RRW)

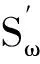
(9)

2.5 速率斜坡(RateRamp，RR)

若陀螺的角速率输出随时间缓慢变化， 比如由环境温度引起， 假设角速率ω与测试时间t之间呈线性变化， 则ω(t)=ω(0)+Rt. 式中R为速率斜坡系数， 或通俗地看成常值加速率误差系数. 直接根据Allan方差的定义可得

(10)

(11)

进一步可得

(12)

表 1 给出了各种误差系数的习惯单位及其与Allan方差的转换关系. 此外在进行Allan方差分析前， 对MEMS陀螺数据采集过程中应考虑采样频率跟采样时间等问题. 采样频率必须满足Nyquist采样定理， 采样频率一般为传感器带宽的3～6倍. 本文中使用的MEMS陀螺带宽为70 Hz， 采用的采样频率为250 Hz. 采样时间至少为1 h， 因为有些误差特性只有在长时间采样下会出现.

3 实验与结果分析

本文利用MEMS陀螺仪搭建了如图 3 的两轴MEMS陀螺组件. 陀螺组件通过RS422输出陀螺原始数据， 并利用上位机进行数据采存. 将陀螺组件安装在三轴温箱转台上， 如图 4 所示. 转台位置精度为5×10-4(360°平均). 通过嵌入式单片利用4 ms的采样周期， 静止采集1 h零偏数据. 得到陀螺组件X轴和Y轴陀螺角速率输出信息， 分别用Allan方差分析方法对两组数据进行处理得到表 2 中的陀螺性能指标.

图 3 MEMS陀螺组件实物图Fig.3 MEMS gyro assembly physical map

图 4 三轴温箱转台Fig.4 The turntable of three axle temperature box

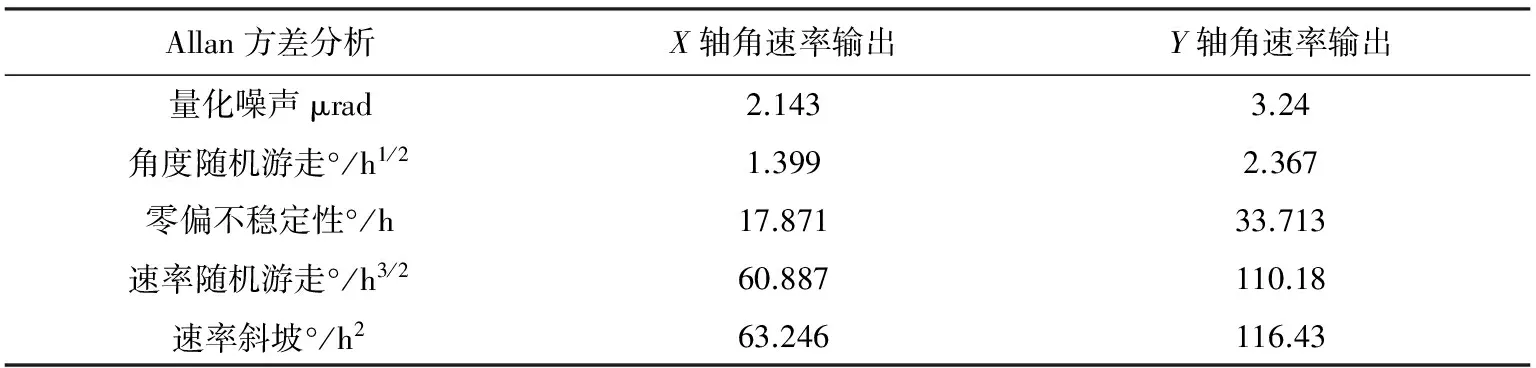
表 2 XY轴角速率输出Allan方差分析结果对比

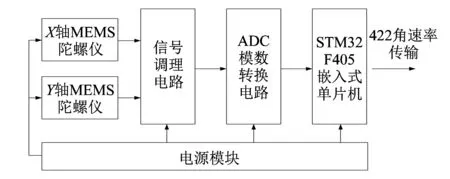
图 5 MEMS陀螺组件系统框图Fig.5 MEMS gyro assembly system diagram

图 6 Allan方差分析曲线图Fig.6 Allan analysis of variance curve

图 5 给出了MEMS陀螺组件设计系统框图. 如图5所示惯组由X轴、Y轴两个正交的MEMS陀螺构成. 陀螺载板的正交性由图5中六面体机械工装保证， 其中该机械工装也作为与三轴精密转台测试时的机械连接装置.X/Y轴陀螺采用模拟输出， 经过5倍放大后输入24 b的高精度ADC中进行模数转换， 再由STM32F405通过SPI协议从ADC中读取数字的角速率信息. 之后嵌入式单片机按照一定的指令协议将角速率数学信号通过422通信传输给上位机软件， 由上位机软件对X/Y轴角速率信息进行实时采存. 最后将采存的角速率文件导入Matlab软件， 进行Allan运算方差处理. 图 6 为Allan方差分析得出的曲线结果.

4 结 论

本文提供了一种MEMS陀螺随机误差分析方法及Allan方差分析法. 该方法能够辨识引起陀螺随机漂移的各项误差来源以及各种误差源的参数指标. 文中给出了Allan方差的定义， 通过各项误差的功率谱建立了零偏不稳定性、 量化噪声、 角度随机游走、 角速率随机游走和速率斜坡与Allan方差之间的关系. 实验部分搭建了两轴MEMS陀螺组件和三轴精密转台实验， 通过采集两轴陀螺零偏数据和matlab数据处理得出了X/Y轴陀螺各项误差参数指标， 验证了本文方法的可行性.

通过Allan方差分析陀螺随机误差参数可以为MEMS陀螺器件设计和加工提供服务还能为陀螺误差补偿建模提供帮助， 能有效提高MEMS陀螺的工程使用精度.

[1] 邹学锋， 卢新艳. 基于Allan方差的MEMS陀螺仪性能评价方法[J]. 微纳电子技术， 2010， 47(8)： 490-493. Zou Xuefeng， Lu Xinyan. Estimate method of MEMS gyroscope perforemance based on allan variance[J]. Micronanoelectronic Technology， 2010， 47(8)： 490-493. (in Chinese)

[2] 王新龙， 李娜．MEMS陀螺随机误差的建模与分析[J]. 北京航空航天大学学报， 2012， 38(2)： 170-174. Wang Xinlong， Li Na. Error modeling and analysis for random drift of MEMS gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics， 2012， 38(2)： 170-174. (in Chinese)

[3] 高宗余， 方建军， 于丽杰. MEMS传感器随机误差Allan方差分析[J]. 仪器仪表学报， 2011， 32(12)： 2863-2868. Gao Zongyu， Fang Jianjun， Yu Lijie. Allan variance analysis for the stochastic error of MEMS sensors[J]. Chinese Journal of Scientific Instrument， 2011， 32(12)： 2863-2868. (in Chinese)

[4] 严恭敏， 李四海， 秦永元. 惯性仪器测试与数据分析[M]. 北京. 国防工业出版社， 2012.

[5] 宋吉磊， 吴训忠， 郭铃. 基于Allan方差法的微机械陀螺误差分析[J]. 导弹与航天运载技术， 2014(2)： 15-17. Song Jilei， Wu Xunzhong， Guo Ling. Application of Allan variance to analysis of micro-electromechanical systems gyroscope error[J]. Missiles and Space Vehicles， 2014(2)： 15-17. (in Chinese)

[6] 张亚宁， 朱涛， 傅军. 基于Allan方差的MEMS陀螺误差分析[J]. 自动化与仪器仪表， 2013(3)： 157-158. Zhang Yaning， Zhu Tao， Fu Jun. Error analysis of MEMS gyroscopebased on Allan variance[J]. Automation and instrumentation， 2013(3)： 157-158. (in Chinese)

[7] 吕品， 刘建业， 赖际舟等. 光纤陀螺的随机误差性能评价方法研究[J]. 仪器仪表学报， 2014， 35(2)： 412-418. Lv Pin， Liu Jianye， Lai Jizhou， et al. Research on the performance evaluation methods of fiber optical gyro stochastic errors[J]. Chinese Journal of Scientific Instrument， 2014， 35(2)： 412-418. (in Chinese)

[8] 郝万亮， 孙付平. 基于Allan方差的陀螺随机误差分析[J]. 测绘与空间地理信息， 2014， 37(3)： 23-25. Hao Wanliang， Sun Fuping. Stochastic errors analysis of gyro based on Allan variance[J]. Geomatics & Spatial Information Technology， 2014， 37(3)： 23-25. (in Chinese)

[9] Sun Jin, Xu Xiaosu， Liu Yiting. FOG random drift signal denoising based on the improved AR model and modified Sage-Husa adaptive Kalman filter[J]. Sensore， 2016， 16(7)： 1073-1078.

[10] 曹慧芳， 吕洪波， 孙启国. 基于MEMS陀螺仪的随机误差分析[J]. 计算机测量与控制， 2016， 24(1)： 178-181. Cao Huifang， Lv Hong bo， Sun Qiguo. Analyses on random error based on MEMS gyroscope[J]. Computer Measurement & Control， 2016， 24(1)： 178-181. (in Chinese)

[11] 李晓莹， 胡敏， 张鹏， 等. 交叠式Allan方差在微机械陀螺随机误差辨识中的应用[J]. 西北工业大学学报， 2007， 25(2)： 225-229. Li Xiaoying， Hu Min， Zhang Peng， et， al. Applying overlapping Allan variance theory to better stochastic modeling of microgyro[J]. Journal of Northwestern Polytechnical University， 2007， 25(2)： 225-229. (in Chinese)

Random Error Analysis Method for MEMS Gyroscope Based on Allan Variance

JIANG Xiaoyong1,2, ZHANG Xiaofeng1, LI Mengwei1,2

(1. Science and Technology on Electronic Test & Measurement Laboratory, North University of China, Taiyuan 030051, China；2. School of Instrument and Electronics, North University of China, Taiyuan 030051, China)

The random drift error of MEMS gyroscope is the main reason to restrict the precision of inertial navigation. In this paper, the main source of random drift error of MEMS gyroscope and the performance parameters of various errors are obtained by Allan variance analysis. This method lays the foundation for analyzing the performance parameters and improving the precision of inertial navigation. In this paper, the definition of Allan variance and the relationship between the random error and Allan variance are introduced. Finally, the MEMS gyro component is built, and the gyro data is collected by high precision turntable experiment. The Allan variance analysis is used to obtain the performance indexes of MEMS gyro, and the feasibility of the method is verified.

MEMS gyroscope； Allan variance； gyro random drift； zero bias instability

1671-7449(2017)03-0190-06

2017-01-05

总装预研基金资助项目(9140A20040515BQ04283)； 总装预研基金资助项目(9140A17060115BQ04241)

蒋孝勇(1992-)， 男， 硕士生， 主要从事MEMS陀螺传感器等研究.

U666.1

A

10.3969/j.issn.1671-7449.2017.03.002