EasySVM:A visual analysis approach for open-box support vector machines
2017-06-19YuxinMaWeiChenXiaohongMaJiayiXuXinxinHuangRossMaciejewskiandAnthonyTung
Yuxin Ma,Wei ChenXiaohong Ma,Jiayi Xu,Xinxin Huang,Ross Maciejewski,and Anthony K.H.Tung
EasySVM:A visual analysis approach for open-box support vector machines
Yuxin Ma1,Wei Chen1Xiaohong Ma1,Jiayi Xu1,Xinxin Huang1,Ross Maciejewski2,and Anthony K.H.Tung3
Support vector machines(SVMs)are supervised learning models traditionally employed for classification and regression analysis.In classification analysis,a set of training data is chosen,and each instance in the training data is assigned a categorical class.An SVM then constructs a model based on a separating plane that maximizes the margin between different classes.Despite being one ofthe most popular classification models because of its strong performance empirically,understanding the knowledge captured in an SVM remains difficult.SVMs are typically applied in a black-box manner where the details of parameter tuning,training,and even the final constructed model are hidden from the users.This is natural since these details are often complex and difficult to understand without proper visualization tools.However,such an approach often brings about various problems including trial-and-error tuning and suspicious users who are forced to trust these models blindly.
The contribution of this paper is a visual analysis approach for building SVMs in an open-box manner. Ourgoalisto improve an analyst’s understanding ofthe SVM modeling process through a suite of visualization techniques that allow users to have full interactive visual control over the entire SVM training process. Our visual exploration tools have been developed to enable intuitive parameter tuning,training datamanipulation,and rule extraction as part of the SVM training process.To demonstrate the efficacy of our approach,we conduct a case study using a real-world robot control dataset.
support vector machines(SVMs); rule extraction;visual classification; high-dimensional visualization;visual analysis
1 Introduction
A support vector machine(SVM)[1]is a supervised learning method widely used in a variety of application areas,such as text analysis[2],computer vision[3],and bioinformatics[4,5].An SVM model is a discriminative model which tries to split the training data into two classes by creating aseparating hyper-planeat the place where the two classes are furthest apart.The class of a new data point is predicted by determining which side of the hyperplane it lies on.
While SVMs have been shown to have high accuracy in classification[6],they also face a variety of challenges when we want to use them for data analytics.First,conventional SVM approaches areblack-boxschemes in which details of the model construction and prediction processes are hidden from the user.The user simply provides the SVM with a training dataset and relevant input parameters,and a model is constructed for making predictions from unlabelled data.Other outputs that can be retrieved from the trained SVM model are a vector that represents the feature weights,and a set oftraining data instances calledsupport vectors. These outputs are unable to provide any insights for domain users who want to better understandthe reasoning behind certain classification results. Thus,while the automatic black-box model releases the user from laborious interaction,it may hinder the user in terms of understanding and insight. Previous work by Tzeng and Ma[7]indicates that users can gain much insight if allowed to apply function-based techniques that can be explained and validated.Such function-based methods enable the interpretation of the classification process with respect to the application domain.The importance of gaining such insight has motivated data mining algorithms[8,9]that try to extractif-then-structuredrules from the classification model.
Another issue that makes gaining insight from SVMs difficult is the use of non-linear kernels[10] which typically improve the classification accuracy. There is,however,a lack of systematic,effective methods to select appropriate kernel functions and input parameters to give good classification results[11].Thus,tuning parameters in this blackbox environment can be extremely difficult and timeconsuming for the user.In addition,the non-linear characteristic further complicates the difficulties of interpreting the classification process.While recently developed local model techniques[11,12] have effectively reduced the complexity of nonlinear SVMs by approximating the boundaries with multiple locallinear planes,interpreting the complex patterns and data distributions at the boundaries remains complicated.
In order to overcome these challenges,we have designed an open-box approach where the user is embedded in the modeling process and equipped with tools to explore and study complex circumstances.We believe the key to shifting from ablack-boxto anopen-boxapproach is to empower the user with a visual analytics interface which will enable a better understanding of SVMs,the underlying dataset,and the classification process. Specifically,our interface design focuses on these three questions:
•Q1:How can we help the user to be better informed about the training dataset and the model building process of SVMs?
•Q2:How can we enable the user to effectively understand non-linear decision boundaries and build local models that fit the boundaries?
•Q3:How can we help the user to interpret and manipulate the prediction results in a user-friendly way?
This paper presents our efforts in opening the black box of model building and knowledge extraction from SVMs.In this paper,we propose our design and implementation ofa web-based visual analysis system that supports model building using SVMs.To the best of our knowledge,this paper is the first to address the issues ofopen-box analysis of SVMs in the visual analytics literature.The main contributions include:
•an interactive visualization method for exploring data instances,linear SVMs,and their relationships;
•a visualanalysis approach for building locallinear SVM models that overcomes the non-linearity of the underlying dataset;
•a visual rule extraction method that allows the user to extract rules that best interpret the models.
The remaining sections are organized as follows. Related work is covered in Section 2.Section 3 presents an introduction to SVMs.The next section describes our visualanalysis solutions for three tasks: modelbuilding and explanation,localSVMbuilding, and rule extraction.Section 5 demonstrates the effectiveness of our solution through a case study on robot control,and is followed by a discussion in Section 6 and conclusions in Section 7.
2 Related work
The work presented in this paper is related to three broad topics:(i)support vector machines,(ii)visual exploration ofhigh-dimensionaldata,and(iii)visual classification.
2.1 Support vector machines
SVMs are currently regarded as a state-of-the-art classification technique[6],and studies have revealed that SVMs perform well when compared to other classification techniques[13].This performance can be partly attributed to the use of non-linear kernels which unfortunately make it difficult to interpret the models.In addition,the production of the boundary function is often quite difficult.Work by Wahba[14]explored the use of SVM functionals to produce classification boundaries,exploring tradeoffs between the size of the SVM functional and the smoothing parameters.
In practice,it is very difficult for non-experiencedusers to tune an SVM[15].However,recently,a set of methods were developed to simplify model complexity while managing non-linearity[16,17]. One representative scheme is to build multiple local models to approximate the global one[11,18,19]. Local modeling methods train a series of linear SVM models near decision boundaries by using training data instances in the corresponding local regions.Unlabelled instances are then classified by the nearest local models in the prediction stage. This method is able to approximate the non-linear boundaries by a series of local linear ones.No intuitive indications are given by the local models about how complex the local regions are,or what kinds of patterns are represented in the regions.
Rule extraction is an important component for the interpretation of SVMs or other classification techniques[20,21].Martens et al.[8]provided a comprehensive study of rule extraction from SVMs. These methods commonly employ an automatic optimization process and result in an axis-parallel representation.However,the targets and interests may vary according to the user and analysis task.It is likely that a visualanalysis process can enable the user to explore both the input parameter space and the classification boundaries.
Unfortunately,there is little work dedicated to visualizing SVMs.Caragea et al.[22]applied a projection method to transform data instances into 2D space.The separating hyper-plane is sampled in the data space,and projected onto the 2D plane.The work by Aragon et al.[23]utilized SVMs as part of a visual analysis system for astrophysics,but provided no general support for SVM exploration.In Ref.[24],we presented an interactive visualization system for visualizing SVMs and providing interactions for users to perform exploration in the dataset.
2.2 Visual exploration of high-dimensional data
One key challenge in opening up SVMs is the need for high-dimensionaldata exploration methods. Recent work in this area has utilized multidimensional projections to map data instances in high-dimensional data space to the lowdimensional(2D)space.The key issue is how to explore the underlying dataset with informative projections.Previous works,such as grand tour[25] and projection pursuit[26],generate a series of projections that allow the user to dynamically explore various lower-dimensional projections of the data in a systematic way in order to find a preferred projection.Other exploration techniques help the user by giving controls for the projection matrix(e.g.,Refs.[27,28]).Nam and Mueller[29] proposed a projection navigation interface,where the exploration and navigation activities are decomposed into five major tasks:sight identification,tour path planning,touring,looking around&zooming into detail,and orientation&localization.Additionally, anN-dimensional touchpad polygon is provided to navigate in high-dimensional space by adjusting the combination of projection weights on each dimension.
Alternatively,high-dimensional data can be visualized with a scatterplot matrix[30],a parallel coordinate plot(PCP)[31,32],or radar charts[33].Previous work has also employed interactive exploration and navigation within scatterplots to fill the gap between projections and axis-based visualization techniques.Elmqvist et al.[34]presented an interactive method to support visualization and exploration of relations between different 2D scatterplots in high-dimensional space. Similarly,3D navigation[35]on the basis of rigid body rotation can be employed for viewing 3D scatterplot matrices.3D rotation interaction improves the user’s ability to perceive corresponding points in different scatterplots for comparison.
2.3 Visual classification
Some visual classification approaches,such as decision and rule-based classifiers[36,37],employ so-calledwhite-boxmodels,in which the detailed process is easy to understand.Teoh and Ma[38] considered the process of building decision trees as a knowledge discovery method,and argued that visualization of the decision tree model can reveal valuable information in the data.Van den Elzen and van Wijk[39]presented a system for interactive construction and analysis of decision trees with operations including growing,pruning,optimization, and analysis.
Another category of work focuses on designing model-transparent frameworks in which the user is allowed to provide training datasets and view the results.Thus,low-level classification techniques canbe directly employed without modification of the analytical process.Heimerl et al.[40]proposed to tightly integrate the user into the labelling process and suggested an interactive binary classifier training approach for text analysis.H¨oferlin et al.[41] presented a system to build cascades of linear classifiers for image classification.
For open-box visual analysis approaches,one of the most similar works to our approach is from Tzeng and Ma[7].It combines several visualization designs for artificial neural networks to open the black box of underlying dependencies between the input and output data.Unlike our interactive visual analysis approach,their open-box scheme is limited to presenting a static visualization of the model structure and does not provide a means of data exploration and interpretation of the classification process.
3 An introduction to SVM classification
Given a set of training data points each withmattributes and an associated class label,the SVM attempts to separate these points using an(m−1)-dimensional hyper-plane.In this section,we will briefly describe this process with the help of Fig.1.
Suppose thatxi∈Rm,i=1,...,n,arentraining data instances in two different classes,andyi∈{−1,+1},i=1,...,n,are their corresponding class labels.A linear support vector machine aims to construct a hyper-plane:

in them-dimensional data space Rmthat has the largest distance to the nearest training data instances of each class(thefunctional margin).
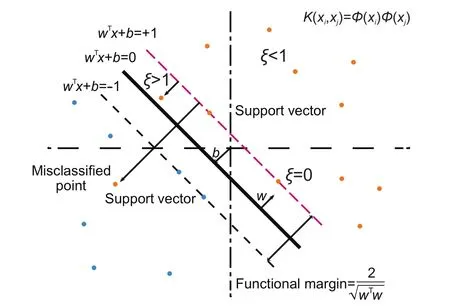
Fig.1 A linear support vector machine.
Equation(1)can be solved by solving the following optimization problem:
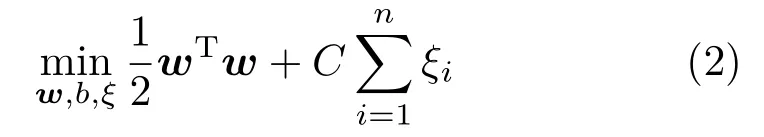
subject toyi(wTxi+b)≥1−ξi,ξi≥0,i=1,...,nwhereCis a user-adjustable parameter to control the relative importance ofmaximizing the margin or satisfying the constraint ofpartitioning each training data instance into the correct half-space.The dual problem to Eq.(2)is derived by introducing Lagrange multipliersαi:
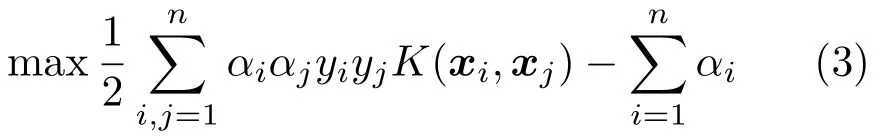
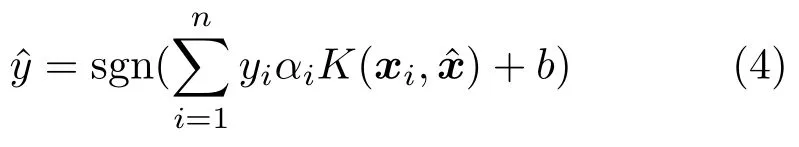
4 EasySVM:Open-box visual modeling of SVMs
As previously stated,the shortcomings of SVMs lie primarily in the fact that they are difficult to interpret and explore.A general visual modeling approach for a linear SVM has two requirements: (i)visualization of the training data instances,the SVM model,and interaction between data instances and model,and(ii)user-guided construction of the SVM model.These basic operations underpin the entire analysis process.Figure 2 shows the analyticalscheme for our solution which consists of three components:

Fig.2 Overview of our approach.
Open-box visual modeling for SVMs. To enable the user to quickly determine item relationships,we map the data instances and SVM models into a 2D plane with an orthogonal projection.We have designed an interactive projection control scheme to support flexible exploration of the dataset and the modelin different ways.
Local SVM building through visualization. Once the data instances and models have been visualized,the user may recognize non-linearities within the model space.The underlying SVM model can then be progressively approximated with a sequence of linear localized SVM models.An integrated suite of visual linkage and comparison operations enable analysts to explore relations between data instances and SVM models as well as to manipulate localmodels.
Visual rule extraction.Rule extraction is interactively performed along each axis.The user can either select segments on the axes or select regions from the projected results of data instances and the SVM models.Each extracted rule can be represented using a hierarchical tree structure.
This scheme is encapsulated in our EasySVM system,a web-based interactive visualization system depicted in Fig.3.The system consists of four main views:a scatterplot view,a projection management view,a dimension selection view,and a rule extraction view.
4.1 Open-box visualmodeling of linear SVM

Fig.3 Interface of EasySVM:(a)the data view,(b)the view ofmultiple projections,(c)the SVM modelbuilding view,(d)the rule extraction view,and(e)the dimension selection view.
The traditional SVM model building process can be summarized as the following fours steps:(i)preprocess the data,(ii)select parameters,(iii) train the model,and(iv)validate the training result[15].If the validation result does not pass the test(i.e.,gives low prediction accuracy on the test dataset),the process is restarted from step(ii) again until it meets the user’s requirements.In our visual model building process,each of these model building steps is enhanced by interactive visualization and visual exploration methods to facilitate understanding during the model building process.Meanwhile,additionaldata exploration and manipulation can be performed during any model building step.Figure 4(a)shows our iterative visual model building process.
Data exploration and initial training.The user can explore the training dataset to approximate the classification boundaries.Then a global model is trained with all training data instances using an initial parameterCin the global SVM model building panel(Fig.3(c)).After this initialstep,the user can perform analysis and operations iteratively using the following two steps.
Visual model exploration and validation. For a trained model,an initial projection is generated in the direction of the side view.The user can evaluate the model starting from the side view to locate misclassified instances,check their distributions and patterns with projections,view the boundaries near the separating hyper-plane, and make decisions on data operations.Compared with the traditionalmachine learning procedure,the visual exploration of the training result provides insight into the reasons why the training result is as it is.Meanwhile,the prediction accuracy on the training dataset is computed and displayed as another reference for modelvalidation.
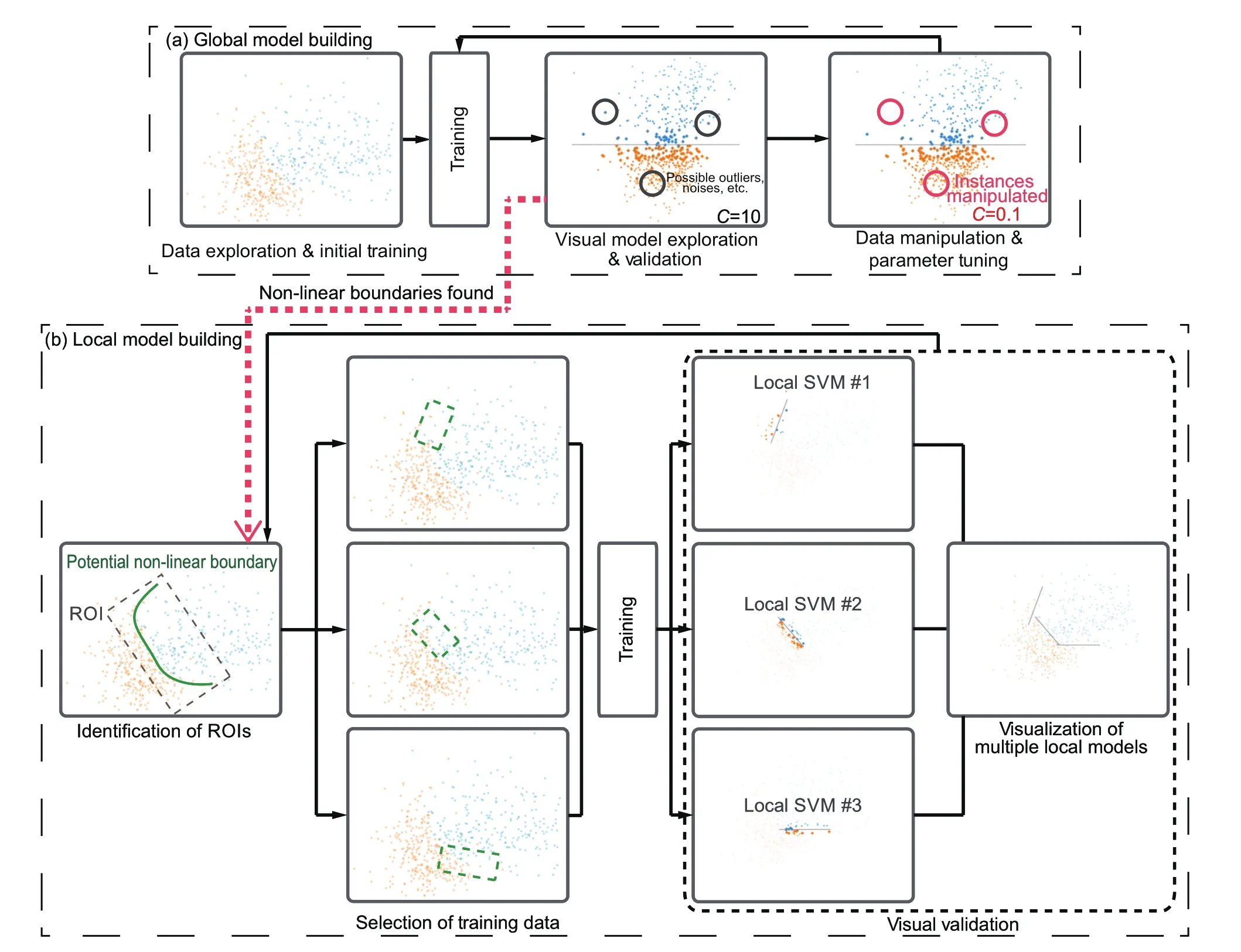
Fig.4(a)Global SVMmodelbuilding process.Ifa non-linear decision boundary is found,the user can enter the localmodelbuilding process (b).
Data manipulation and parameter tuning. After exploration,some training data instances that affect model building can be modified by changing their labels or deleting them from the dataset ifthey are considered to be noise or instances with invalid values.In addition,the parameterCcan be tuned in this step to balance the trade-off between margins of the hyper-plane and prediction accuracy on the training dataset.It is required to re-train the model after these two operations to update the model and classification results.The model building process stops when the validation result satisfies the user’s requirements,such as prediction accuracy on a test dataset.It should be noted that for a dataset with non-linear,complex decision boundaries,locallinear models are needed.
4.1.1 Visualization of training data and the SVM model
The data view(see Fig.3(a))in our system is based on a scatterplot in which data instances are projected into a low-dimensional subspace.We use an orthogonalprojection to embed high-dimensional data instances and the SVM model in a 2D plane. This view features two panels:a top menubar that contains exploration tools for the scatterplot,and a projection control panel that provides visualization of the dimension axes and control methods for interactive projection control.Two reasons for providing this are:(i)it is a powerful technique for visualizing the training dataset,and(ii)it simultaneously makes clear the geometricalrelations between data instances and the hyper-plane,like relative positions and distances between each other that are essential for the user to understand the structure of SVM models.
Orthogonal projection.Given an orthogonal projection matrixAm×2=[f1,f2],twomdimensional vectorsf1,f2span a 2D plane in them-dimensional data space onto which all data instances are projected.Applying it to a highdimensional data instance yields a corresponding data point on the 2D plane,i.e.,the coordinates of the data point in the scatterplot view=xiA.It should be noted that the 2D projection formula of the separating hyper-plane is very hard to find.We first sample a set of points on the separating hyperplane,and then project sample points onto the 2D plane to approximate the hyper-plane.Specifically, the sample procedure contains the following four steps:
1.project all training data instances onto the separating hyper-plane;
2.calculate a bounding-box ofthe projections in step (1);
3.uniformly sampleNsamplepoints in the boundingbox on the separating hyper-plane;
4.project theNsamplesample points onto the 2D plane withA.
Visual encoding.To encode the data instances, three visual channels are employed as illustrated in Fig.5.The input label of each data instance is encoded with a filled color.If the predicted labelby the SVM is different from its input label,a border color other than the filled color is employed.The shape represents whether a data instance is a support vector;we use a rectangle for a support vector and a circle otherwise.Furthermore,the opacity of a data instance encodes the distance from the corresponding separating plane.
For the separating hyper-plane ofthe SVM model, the sample points are drawn on the view as dots in grey with a smaller size than the data points(shown in Fig.6(a)).Additionally,to visualize the density of training data instances,a density map is computed and rendered.For each class,the density maps oftwo colors are generated separately,then the two maps are composed on the view.Figure 6(b)shows the result.

Fig.5 Our visual encoding scheme.
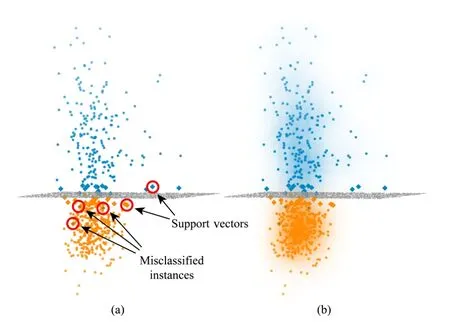
Fig.6 Examples of projections:(a)visual encoding applied to data points,(b)a density map composition.
4.1.2 Visual exploration of the projected scatterplotIn our visual exploration,an interactive projection control method is provided for manipulating the direction of the selected projection.Our method is based on Ref.[28],where the control is similar to the trackball control in a high-dimensional data space.A weight is specified first for each dimension to determine which one is going to be manipulated, then the user can rotate the projection plane by dragging the mouse in the scatterplot view. Finally the user’s mouse action is translated into a rotation matrix and applied to the projection matrix, thus changing the scatterplot.However,a gimbal lock problem exists in the method,which limits the rotation at the singular point.We improve their method by using quaternions to compute the rotation to avoid this issue.
To assist the user in the exploration of the relationships between multiple projections,we offer a view of multiple projections(Fig.3(b)).Each projection glyph holds a snapshot of the interesting scatterplot inside the glyph with the projection matrix.We define the similarity between two projection glyphs as the Euclidean distance between two corresponding projection matrices,i.e.,‖A1−A2‖2.Thus,the layout of the glyphs is determined using a local affine multi-dimensional projection algorithm[42].The user can plan a rotation path containing a sequence of projection glyphs among the multiple projection glyphs,then a rotation animation is generated based on interpolation between adjacent projections along the path[27] with a slider to controlthe position ofthe animation.
Two categories of exploration actions can be performed to extract knowledge from the dataset and SVM model.
Data distributions,clusters,or outliers. Data distributions and patterns in the projections indicate the potential location and direction of a separating plane.The exploratory discovery of distributions and patterns can be performed at each stage of the analytical process.For example,before training any SVM models,the user can explore the training dataset to inspect boundaries between two classes;after an SVM model is trained,data distributions along the separating hyper-plane and specific patterns in support vectors,such as outliers, may illuminate the direction of further exploration, label manipulation,or parameter tuning.
Side views of the separating hyper-plane. When one of the basis vectorsf1,f2is equal to the weight vectorwof the SVM model,all the sample points will be projected into a line in the view.This can be easily proved:letf1=w,for all sample points withwTx+b=0;the coordinates off1are constant.We call a view under this kind of projection matrix aside view.Figure 7 shows some examples of a side view.Side views are useful when investigating or validating a trained model,because:
•the boundaries of each class and gaps between them are shown clearly in the projection;
•the distance from each data point to the hyperplane on a 2D plane and the actual distance in high-dimensional data space are in the same proportion,leading to an intuitive illustration of the spatial relations between training data instances and the separating hyper-plane.
A useful exploration strategy is to start from the side view ofthe separating hyper-plane.The user can rotate the projection through a smallrange ofangles using interactive projection control,allowing data distributions near the hyper-plane to be displayed and explored.
Orthogonal projection is unable to show highdimensional data separation which may cause profound visual clutter.A dimension selection view(Fig.3(e))is provided for filtering out noninformative dimensions in the classification task.Inthis view,three bar charts rank all the dimensions of the training data instances according to three measures:correlation coefficients between the dimension and the class labels,signal-to-noise ratio, and weighting by a linear SVM[43].The user can select the most informative dimensions,which will be highlighted in the candidate list.After the selection is confirmed,the projected scatterplot will be updated to apply the changes.Dimensions that are filtered out will not take part in the projection process and the future model building process.
4.2 Visual local SVM building
For clarity,we use the termglobal modelto represent the SVM model built with the process described in Section 4.1,which covers all the training data instances in the dateset.Alocal model,on the contrary,is trained on a selected subset of training data instances.
4.2.1 Visual exploration of decision boundaries
Before building local SVM models,it is necessary to perform a preliminary exploration of the decision boundary and an evaluation of complexity.First, it is necessary to explore the data distributions, because the data distribution near the decision boundaries is a strong indication of the boundary complexity.The user can control the projection interactively and inspect the patterns of boundaries between pairs ofclasses ofdata points.Additionally, the user can explore the decision boundaries guided by the global SVM model.Although not applicable to low prediction accuracy in complex circumstances, the separating hyper-plane of the global SVM model can act as a guide to the decision boundary.Training data instances lying on opposite sides of the hyperplane always imply local regions containing nonlinear boundaries,or even non-classifiable areas with mixed distributions ofa pair ofclasses.The user can locate the regions in the projected scatterplot,check the patterns visually,and make further analysis.
4.2.2 Visual local model building process
Our visual local model building process extends the previous globalone in Section 4.1.The key issues are to(i)locate regions-of-interest,and(ii)select proper subsets oftraining data instances for each localSVM model.We propose the following four steps to build local models iteratively(see Fig.4(b)).
Identification of regions-of-interest.The target regions are located using the visual exploration methods given in Section 4.2.1.It should be pointed out that when some local models have been created,any of them,not just the global model,can be considered as a starting point for visual exploration and location.Local models with different numbers of training data instances and ranges of coverage in high-dimensional data spaces will provide diverse levels of details.The user can select the starting point as desired.
Selection of training data instances.The training data instances of a new local model can be selected directly by user interaction in the projection view.Moreover,we propose a hierarchical model creation method based on split-and-merge operations on the models created.A local model can be split into two new ones by dividing its corresponding training dataset into two subsets and training two new models on each subset.The training data instances from several models can also be merged together.A new localmodelis trained on the merged dataset to replace the existing ones.Both operations change the level of detail,in opposite directions.When a model is split into several multiple ones,the details of the decision boundary can be made more precise,while in merging,a set of models carrying much detailed information is replaced by a generalized model.Such level-ofdetail exploration and incremental model creation allow the user to determine the decision boundaries and understand the distributions.
Training.Once the parameterCis set for each model,the newly created or updated local models are re-trained in this step.
Validation.In this step,the training result is validated in two ways.For a single local model,the same validation methods for the global model are applied;for checking relations and coverage between multiple models,the projection rotations between multiple models can be considered as indications of their positions and directions.
After the local model building process is done, the models can be employed for predicting new data instances.A prediction algorithm is provided based on the set oflocalmodels,where the query instances are labeled by the nearest local SVM.Algorithm 1 gives the prediction process.
Algorithm 1 Prediction procedure of local SVMs Input:

4.2.3 Visualization and interactions of multiple models
Statistical information about existing local SVM models is displayed.In particular,a matrix is used to encode the similarity between allmodels in terms of the number of shared training data instances.Each matrix cell(i,j)is defined as
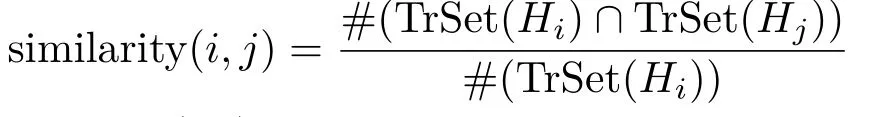
where TrSet(Hi)is the training dataset of theith local model.The matrix is visualized with an opacity-modulated color(green in our system),as shown in Fig.3(c).The opacity of each cellis set to its similarity.
Note that the side view best depicts the structure of a linear SVM model,while rotating from the side view of a local model to another can depict the spatial relations between different models.This is done by taking side view snapshots for each modeland creating a rotation path through multiple projections.
4.3 Visual rule extraction
By a rule we mean a small-sized canonical subspace of the input high-dimensional data space that may encapsulate some domain knowledge.The subspace is bounded by a set of dimension intervals,each of which refers to one or severalranges of a dimension. Thus,determining a rule is identical to specifying one or severalintervals in each dimension.Each rule denotes a class and assigns the corresponding class labelautomatically to the data instances in the rule.
As shown in the rule extraction view(see Fig.3(d)),we apply the flexible linked axes method[44]to visualize the training data instance. The positions and orientations ofthe dimension axes can be arranged freely.Between pairs of axes,the data instances are represented by parallelcoordinate plot-styled edges or scatterplot-styled dots.The reason is that this allows the user to choose desired dimensions based on their importance,and visualize the data distributionsin one dimension(on axis),two dimensions(in a scatterplot),or multiple dimensions (in a parallelcoordinate plot).
The following two interaction methods are provided for specifying classification rules.
Brushing line plots.The user directly brushes the axis to select a range.Note that the number of training data instances included in a range should be maximized,as more training data instances lead to higher confidence in the rule when classifying new instances.
Selecting points in the projected scatterplot.Selection of data points in the projected scatterplot is linked in the rule extraction view.When selecting an interesting cluster of data instances in the projected scatterplot,the corresponding dots or edges are highlighted,as well as the range of their bounding-box on each axis.
After the set of selected ranges is committed,a new rule glyph that represents the set of ranges, i.e.,the rule,is displayed.In the rule glyph,a parallelcoordinate plot is provided to summarize the dimension intervals.The background color of the rule glyph encodes its expected class with a unique color.Next the user is given the option to explore the relations between different rules for further optimization.To express the similarity between two rules,we use the force-direct layout based on the Jaccard index between the sets of training data instances in two separate rules as the similaritymeasure.This layout enables a better understanding of their intersecting areas.For instance,the glyphs that are close to each other may be redundant.
5 Case study
5.1 System implementation
EasySVMis primarily implemented inJavaScriptfor its front-end UI,employingD3.jsas graphic rendering library,thejQueryUI for user interface components,andBackbone.jsas the MVC framework.For back-end computational support, we designed a RESTfulinterface for communication built on theDjangoWeb Framework,and applyscikit-learnas the SVM implementation.
5.2 Wall-following Robot Navigation dataset
For the Wall-following Robot Navigation dataset [45],four moving actions(Move-Forward,Slight-Right-Turn,Sharp-Right-Turn,andSlight-Left-Turn)are to be determined based on the input values from 24 ultrasound sensors(US0–US23).Given a series of sensor values,a classifier is supposed to be trained for predicting the best action.We only use the data instances inMove-ForwardandSharp-Right-Turnin our binary classification(4302 instances in total)and divide the dataset into two parts:50 percent as the training set,and the other 50 percent as the test set.
Data exploration.See Fig.9(a).By default,the initial projected scatterplot is the same as the 2D scatterplot with only the first two dimensions(US0, US1).The user starts from this initialprojection and performs interactive projection control by selecting each of the other dimensions(US2–US23).While manipulating dimension US14,a coarse gap appears on a large branch on the right side,which indicates a potential linear boundary.However,training datainstances of diff erent classes in a smaller branch on the left side are overlapping,which seem impossible to linearly separate.A snapshot is taken to support further investigation.
Global SVM model building.See Fig.9(b). After preliminary data exploration,the user trains a global SVM model with all training data instances. However,the accuracy on the training dataset is around 80%for various settings of parameterC, meaning that the dataset is not linearly separable.In the side view,a set of wrongly-classified instances is observed,scattered near the separating hyper-plane.
Local SVM model building.See Fig.9(b). The user manipulates dimension US14 again to investigate the probable boundary found earlier, while the separating hyper-plane is located in a different direction.Now the user decides to build two separate models for the two branches.After training two local SVM models,two side views show that the two corresponding separating hyper-planes are in different directions and give better separation in the regions near their training datasets,which is also indicated by the two accuracy values(around 91%for the model on the smaller branch and 94% for the one on the larger branch).Animated rotation between the side views of the global model and the two local models partially depicts the relations between three separating hyper-planes.Thus,the global SVM modelis replaced by the two locallinear ones.
Rule extraction.See Fig.9(c).Rule extraction operations are assisted by the two localmodels.The user chooses to extract rules for the local model on the large branch.From the weight vector of the local model,it is obvious that dimensions US14 and US20 dominate the direction ofthe separating hyperplane.Thus the user constructs a parallelcoordinate plot linking US14 and US20.The user brushes three combinations ofranges on the two axes and generates three rules.
Prediction accuracy.The global linear SVM achieves 81%±1.0%prediction accuracy on the test set,while the local SVM models achieve 88%±3.0%.
6 Discussion
In terms of non-linear SVM model building,our approach presents an approximation method using multiple linear models,which can be utilized as an interpretation tool of the original training dataset and a prediction toolfor future unlabelled instances. For example,each local linear SVM interprets the boundary in a local area with its separating hyperplane,while a prediction can also be made with thek-NN prediction algorithm.
The trade-off between complexity and interpretability is important for building local SVMs.Increasing the number of locallinear models will help to approximate the non-linear decision boundary more accurately.However,it increases the difficulty for the user to understand the decision boundary at the same time.Meanwhile,some local models may be redundant because they hold almost the same information as other local models.In addition,for a training dataset containing noise around the decision boundary,over-fitting may happen if some local models represent detailed information from the noise.
One promising extension of our approach is to improve its scalability,including the number of training data instances as well as the number of dimensions.For massive amounts of data,clustering methods can be adopted before projection to reduce the visualclutter caused by too many data points in the 2D plane.For the dimensionality issue,we need to design a more scalable visual dimension selection procedure to reduce the number of dimension candidates before projection is performed.
7 Conclusions
In this paper,we have proposed a novel open-box visual analysis approach for building SVM models. The user can perform visual exploration of the dataset and the relations between data instances and SVM models.Meanwhile,a visually-enhanced local linear model building approach is dedicated to expanding the traditional linear SVM to deal with non-linear decision boundaries.Finally we provide a visual rule extraction method to enable the user to retrieve classification rules from the model building results.
Acknowledgements
This work was supported in part by the National Basic Research Program of China(973 Program, No.2015CB352503),the Major Program ofNational Natural Science Foundation of China (No.61232012),and the National Natural Science Foundation of China(No.61422211).
Electronic Supplementary Material Supplementary material is available in the online version of this article at http://dx.doi.org/10.1007/s41095-017-0077-5.
[1]Cortes,C.;Vapnik,V.Support-vector networks.Machine LearningVol.20,No.3,273–297,1995.
[2]Tong,S.;Koller,D.Support vector machine active learning with applications to text classification.Journal of Machine Learning ResearchVol.2,45–66, 2001.
[3]Osuna,E.;Freund,R.;Girosi,F.Training support vector machines:An application to face detection.In: Proceedings ofthe IEEE Computer Society Conference on Computer Vision and Pattern Recognition,130–136,1997.
[4]Furey,T.S.;Cristianini,N.;Duffy,N.;Bednarski, D.W.;Schummer,M.;Haussler,D.Support vector machine classification and validation of cancer tissue samples using microarray expression data.BioinformaticsVol.16,No.10,906–914,2000.
[5]Hasenauer,J.;Heinrich,J.;Doszczak,M.;Scheurich, P.;Weiskopf,D.;Allg¨ower,F.A visual analytics approach for models ofheterogeneous cellpopulations.EURASIP Journal on Bioinformatics and Systems BiologyVol.2012,4,2012.
[6]Abe,S.Support Vector Machines for Pattern Classification.Springer London,2010.
[7]Tzeng,F.-Y.;Ma,K.-L.Opening the black box—Data driven visualization of neural networks.In: Proceedings ofthe IEEE Visualization,383–390,2005.
[8]Martens,D.;Baesens,B.B.;van Gestel,T. Decompositional rule extraction from support vector machines by active learning.IEEE Transactions on Know ledge and Data EngineeringVol.21,No.2,178–191,2009.
[9]N´u˜nez,H.;Angulo,C.;Catal`a,A.Rule extraction from support vector machines.In:Proceedings of the European Symposium on Artificial Neural Networks, 107–112,2002.
[10]Sch¨olkopf,B.;Smola,A.J.Learning with Kernels:Support Vector Machines,Regularization, Optimization,and Beyond.MIT Press,2002.
[11]Ladicky,L.;Torr,P.Locally linear support vector machines.In:Proceedings of the 28th International Conference on Machine Learning,985–992,2011.
[12]Ganti,R.;Gray,A.Local support vector machines:Formulation and analysis.arXiv preprintarXiv:1309.3699,2013.
[13]Baesens,B.;Gestel,T.V.;Viaene,S.;Stepanova, M.;Suykens,J.;Vanthienen,J.Benchmarking stateof-the-art classification algorithms for credit scoring.Journal of the Operational Research SocietyVol.54, No.6,627–635,2003.
[14]Wahba,G.Support vector machines,reproducing kernel Hilbert spaces,and randomized GACV.In:Advances in Kernel Methods.Sch¨olkopf,B.;Burges, C.J.C.;Smola,A.J.Eds.Cambridge,MA,USA: MIT Press,69–88,1999.
[15]Hsu,C.-W.;Chang,C.-C.;Lin,C.-J.A practical guide to support vector classification.2016.Available at http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide. pdf.
[16]Mangasarian,O.L.;Wild,E.W.Proximal support vector machine classifiers.In:Proceedings of KDD-2001:Knowledge Discovery and Data Mining,77–86, 2001.
[17]Maji,S.;Berg,A.C.;Malik,J.Classification using intersection kernelsupport vector machines is efficient. In:Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,1–8,2008.
[18]Blanzieri,E.;Melgani,F.An adaptive SVM nearest neighbor classifier for remotely sensed imagery.In: Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing,3931–3934,2006.
[19]Yin,C.;Zhu,Y.;Mu,S.;Tian,S.Localsupport vector machine based on cooperative clustering for very largescale dataset.In:Proceedings of the 8th International Conference on Natural Computation,88–92,2012.
[20]Barakat,N.H.;Bradley,A.P.Rule extraction from support vector machines:A sequential covering approach.IEEE Transactions on Know ledge and Data EngineeringVol.19,No.6,729–741,2007.
[21]Fung,G.;Sandilya,S.;Rao,R.B.Rule extraction from linear support vector machines.In:Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining,32–40,2005.
[22]Caragea,D.;Cook,D.;Wickham,H.;Honavar,V. Visual methods for examining SVM classifiers.In:Visual Data Mining.Simoff,S.J.;B¨ohlen,M.H.; Mazeika,A.Eds.Springer Berlin Heidelberg,2007.
[23]Aragon,C.R.;Bailey,S.J.;Poon,S.;Runge,K. J.;Thomas,R.C.Sunfall:A collaborative visual analytics system for astrophysics.In:Proceedings of the IEEE Symposium on Visual Analytics Science and Technology,219–220,2007.
[24]Ma,Y.;Chen,W.;Ma,X.;Xu,J.;Huang,X.; Maciejewski,R.;Tung,A.K.H.EasySVM:A visual analysis approach for open-box support vector machines.In:Proceedings of the IEEE VIS 2014 Workshop on Visualization for Predictive Analytics, 2014.
[25]Asimov,D.The grand tour:A tool for viewing multidimensional data.SIAM Journal on Scientific and Statistical ComputingVol.6,No.1,128–143,1985.
[26]Friedman,J.H.;Tukey,J.W.A projection pursuit algorithm for exploratory data analysis.IEEE Transactions on ComputersVol.C-23,No.9,881–890, 1974.
[27]Buja,A.;Cook,D.;Asimov,D.;Hurley,C. Computational methods for high-dimensionalrotations in data visualization.In:Handbook of Statistics,Volume 24:Data Mining and Data Visualization.Rao,C.R.;Wegman,E.J.;Solka,J. L.Eds.Amsterdam,the Netherlands:North-Holland Publishing Co.,391–413,2005.
[28]Cook,D.;Buja,A.Manual controls for high-dimensional data projections.Journal of Computational and Graphical StatisticsVol.6,No.4, 464–480,1997.
[29]Nam,J.E.;Mueller,K.TripAdvisorN−D:A tourism-inspired high-dimensional space exploration framework with overview and detail.IEEE Transactions on Visualization and Computer GraphicsVol.19,No.2,291–305,2013.
[30]Cleveland,W.C.;McGill,M.E.Dynamic Graphics for Statistics.Boca Raton,FL,USA:CRC Press,1988.
[31]Inselberg,A.The plane with parallel coordinates.The Visual ComputerVol.1,No.2,69–91,1985.
[32]Inselberg,A.;Dimsdale,B.Parallel coordinates:A tool for visualizing multi-dimensional geometry.In: Proceedings of the 1st Conference on Visualization, 361–378,1990.
[33]Chambers,J.M.;Cleveland,W.S.;Kleiner,B.;Tukey, P.A.Graphical Methods for Data Analysis.Duxbury Press,1983.
[34]Elmqvist,N.;Dragicevic,P.;Fekete,J.D.Rolling the dice:Multidimensional visual exploration using scatterplot matrix navigation.IEEE Transactions on Visualization and Computer GraphicsVol.14,No.6, 1539–1148,2008.
[35]Sanftmann,H.;Weiskopf,D.3D scatterplot navigation.IEEE Transactions on Visualization and Computer GraphicsVol.18,No.11,1969–1978,2012.
[36]Liu,B.;Ma,Y.;Wong,C.K.Improving an association rule based classifier.In:Principles of Data Mining and Know ledge Discovery.Zighed,D.A.;Komorowski,J.; ˙Zytkow,J.Eds.Springer Berlin Heidelberg,504–509, 2000.
[37]Quinlan,J.R.Induction of decision trees.Machine LearningVol.1,No.1,81–106,1986.
[38]Teoh,S.T.;Ma,K.-L.PaintingClass:Interactive construction,visualization and exploration of decision trees.In:Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,667–672,2003.
[39]Van den Elzen,S.;van Wijk,J.J.BaobabView: Interactive construction and analysis of decision trees. In:Proceedings of the IEEE Conference on Visual Analytics Science and Technology,151–160,2011.
[40]Heimerl,F.;Koch,S.;Bosch,H.;Ertl,T.Visual classifier training for text document retrieval.IEEE Transactions on Visualization and Computer GraphicsVol.18,No.12,2839–2848,2012.
[41]H¨oferlin,B.;Netzel,R.;H¨oferlin,M.;Weiskopf,D.; Heidemann,G.Inter-active learning of ad-hoc classifiers for video visual analytics.In:Proceedings of the IEEE Conference on Visual Analytics Science and Technology,23–32,2012.
[42]Joia,P.;Coimbra,D.;Cuminato,J.A.;Paulovich, F.V.;Nonato,L.G.Local affine multidimensional projection.IEEE Transactions on Visualization and Computer GraphicsVol.17,No.12,2563–2571,2011.
[43]Guyon,I.;Elisseeff,A.An introduction to variable and feature selection.Journal of Machine Learning ResearchVol.3,1157–1182,2003.
[44]Claessen,J.H.T.;van Wijk,J.J.Flexible linked axes for multivariate data visualization.IEEE Transactions on Visualization and Computer GraphicsVol.17,No. 12,2310–2316,2011.
[45]Freire,A.L.;Barreto,G.A.;Veloso,M.;Varela,A. T.Short-term memory mechanisms in neural network learning of robot navigation tasks:A case study. In:Proceedings of the 6th Latin American Robotics Symposium,1–6,2009.

Yuxin Ma is a Ph.D.student in the State Key Lab of CAD&CG,Zhejiang University.His current research focuses on information visualization,visual analytics,and visual data mining.

Wei Chen is a professor in the State Key Lab of CAD&CG,Zhejiang University.He has published more than 60 papers in international journals and conferences.He served as steering committee of IEEE Pacific Visualization,conference chair of IEEE Pacific Visualization 2015,and paper co-chair of IEEE Pacific Visualization 2013.For more information,please refer to http://www.cad. zju.edu.cn/home/chenwei/.

Xiaohong Ma is a master student in the State Key Lab of CAD&CG, Zhejiang University.Her current research focus is information visualization.

Jiayi Xu is a Ph.D.candidate in the Department of Computer Science and Engineering,Ohio State University.He received his B.E.degree in the School of Computer Science and Technology, Zhejiang University.His research interest is information visualization.

Xinxin Huang is a master student in the State Key Lab of CAD&CG, Zhejiang University.Her current research focuses are information visualization and visual analytics, especially visual analytics of sports data.

Ross Maciejewski is an assistant professor in Arizona State University (ASU).His recent work has actively explored the extraction and linking of disparate data sources exploring combinations of structured geographic data to unstructured social media data to enhance situational awareness.His primary research interests are in the areas of geographical visualization and visualanalytics focusing on public health, dietary analysis,socialmedia,and criminalincident reports. He is a fellow of the Global Security Initiative in ASU and the recipient of an NSF CAREER Award(2014).

Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License(http:// creativecommons.org/licenses/by/4.0/),which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.
Other papers from this open access journalare available free ofcharge from http://www.springer.com/journal/41095.To submit a manuscript,please go to https://www. editorialmanager.com/cvmj.
.H.Tung
his B.S. (second class honor)and M.S.degrees in computer science from the National University of Singapore(NUS),in 1997 and 1998,respectively,and Ph.D.degree in computer science from Simon Fraser University in 2001.He is currently an associate professor in the Department of Computer Science,NUS.His research interests include various aspects of databases and data mining(KDD) including buff er management,frequent pattern discovery, spatial clustering,outlier detection,and classification analysis.
1 State Key Lab of CAD&CG,Zhejiang University, Hangzhou,310058,China.E-mail:Y.Ma,mayuxin@ zju.edu.cn;W.Chen,chenwei@cad.zju.edu.cnX.Ma,maxiao1112@foxmail.com;J.Xu,jiayi.xu64@ gmail.com;X.Huang,huangxinxin07@gmail.com.
2 Arizona State University,USA.E-mail:rmacieje@ asu.edu.
3 National University of Singapore,Singapore.E-mail: atung@comp.nus.edu.sg.
Manuscript received:2016-12-24;accepted:2017-01-09
杂志排行
Computational Visual Media的其它文章
- Robust camera pose estimation by viewpoint classification using deep learning
- Feature-aligned segmentation using correlation clustering
- Fast and accurate surface normal integration on non-rectangular domains
- User-guided line abstraction using coherence and structure analysis
- Feature-based RGB-D camera pose optimization for real-time 3D reconstruction
- View suggestion for interactive segmentation of indoor scenes
