基于相似系数和Jaccard系数矩阵的证据冲突度量方法

2017-06-19孟晨晨肖建于

重庆邮电大学学报(自然科学版) 2017年3期

关键词：子集度量框架

孟晨晨，肖建于，罗兰

(淮北师范大学计算机科学与技术学院，安徽淮北 235000)

基于相似系数和Jaccard系数矩阵的证据冲突度量方法

孟晨晨，肖建于，罗兰

(淮北师范大学计算机科学与技术学院，安徽淮北 235000)

针对传统的冲突度量和Jousselme距离度量出现冲突误判的问题，提出一种相似系数和Jaccard系数矩阵的证据冲突度量方法。该方法通过计算证据之间的相似系数，利用Jaccard系数矩阵将相似系数转化为证据的冲突程度。理论证明和数值计算表明，该方法可以有效地表示证据间的冲突程度。此外，通过典型的算例将提出的方法与其他方法进行对比，结果表明该方法可以全面准确地度量证据间的冲突程度。

D-S证据理论; 冲突度量; 相似系数; Jaccard系数矩阵

0 前言

D-S证据理论[1]可以处理各种不确定和不完善的信息，现已广泛应用于空中目标识别，决策支持，故障检测等领域中。如果证据间存在高度冲突时，使用传统的Dempster组合规则常常会导致悖论。但是，如何度量冲突证据目前还没有一个统一的衡量标准。文献[2-3]定义矩阵的奇异值来度量冲突证据，得到较好的效果。文献[4]将蒋雯的表达式推广到更一般的形式，实验表明该方法能够衡量证据间的冲突程度。文献[5-9]分别重新定义关联系数、相关系数来度量冲突证据。文献[10]从证据的非对称性出发，提出了一种非对称的证据冲突度量方法。文献[11-12]均从改进Jousselme距离出发，修正传统的度量证据冲突的方法。文献[13]引入不确定度来度量证据，以此修正组合规则。文献[14-15]将辨识框架推广到广义的幂集空间中，建立一种处理证据冲突的度量模型。文献[16-18]从优化的角度出发，进行冲突度量。

本文拟从证据的相似性角度出发，定义证据的相似系数，并结合Jaccard系数矩阵来共同度量证据间的冲突程度。通过这种方法来判断证据间是否存在冲突，以此来决定采取何种组合方法。

1 两种冲突度量方法

定义1 在辨识框架Θ下的2个基本概率赋值函数分别为m1,m2，Dempster组合规则[1]定义为

(1)

(2)

(1)—(2)式中，k∈[0,1)为冲突系数，通常用k来度量证据间的冲突程度。

定义2 假设在辨识框架Θ下的2个基本概率赋值函数分别为m1,m2，Jousselme距离定义为[19]

(3)

例1 假设辨识框架Θ={a,b,c,d,e}，系统中的证据如下

m1(a)=m1(b)=m1(c)=m1(d)=m1(e)=0.2，

m2(a)=m2(b)=m2(c)=m2(d)=m2(e)=0.2。

利用(2)式计算得出k=0.800 0,表明证据间存在高度冲突，而利用(3)式计算出dBPA=0.0000，表明证据间不存在冲突。但从直观上看，这2条证据是完全一致的，并不存在冲突，与dBPA的判断一致。所以用(1)式会得出与实际相反的结果，会造成冲突的误判。

此时，说明冲突系数k不能表征证据之间的冲突，但是利用Jousselme中的dBPA也存在不能表征证据之间的冲突问题。

例2 假设在辨识框架Θ={a,b,c,d}下，系统中的2组证据分别为

从例1和例2可以看出，利用冲突系数k和dBPA均可能造成证据的误判。

针对此类问题，文献[5]提出基于随机变量的偏熵和关联熵的关联系数，虽然关联系数在同一性检验、一致性分析领域应用较广泛，但是，在证据中存在0项时，计算时会出现log0=-∞，为了避免出现以上情况，采取的近似计算具有一定的工程意义，但是，无法从物理意义上进行解释。

文献[6]利用Joussleme证据距离转化为广义的证据距离，并将其中的参数转换为Hausdorff距离和相似矩阵之和来共同表征证据之间的冲突程度。但是，其参数的设定具有主观臆断性，对于多个证据之间的冲突问题则无法很好地表征。

文献[18]将k和Pignistic概率距离组成二元组，但是，并没有提出一个公式来统一这2个因子，只是单纯地根据阈值来判断证据是否冲突，主观臆断较明显。

2 一种新的冲突度量方法

针对k和dBPA存在冲突误判的情况以及前人研究中的一些客观存在的问题，如：传感器自身的问题；传感器系统受到外界环境(如气象灾害、敌方人为的干扰)的影响，导致测量的不准确；辨识框架的不完整；参数阈值确定的主观性等。故本文提出一种基于相似系数和Jaccard系数矩阵的方法来度量证据冲突程度。

定义3 假设在辨识框架Θ下的2个基本概率赋值函数分别为m1,m2，则相似系数定义为

(i,j= 1,…,N)

(4)

sim具有以下的性质：

1)sim(m1,m2)∈[0,1]

2)sim(m1,m2)=1⟺m1(Ai)=m2(Bj)

3)sim(m1,m2)=sim(m2,m1)

4)(∪Ai)∩(∪Bj)=∅，当且仅当sim(m1,m2)=0。其中，Ai,Bj分别为证据mi(·),mj(·)所对应的焦元。

证明：

1)假设在辨识框架Θ下的基本概率函数m1,m2表示的向量为

m1=[m1(A1),m1(A2)…,m1(AN)]

m2=[m2(B1),m2(B2)…,m2(BN)]

∴左式=

由柯西不等式可知

||≤|m1||m2|

当且仅当m1=m2，取等号

∵m1,m2的各个分量的值均为非负数，

∴=m1m2Τ≥0

∴sim(m1,m2)∈[0,1]。

性质1)证毕。

2)在性质1)的证明中，不等式取等号的条件是：m1=m2.

∴性质2)证毕。

3)sim(m1,m2)=sim(m2,m1)显然成立。

4)∵(∪Ai)∩(∪Bj)=∅

∴表示2个证据之间没有公共的焦元。

假设m1中的坐标分量m1(Ai)≠0，则m2对应的坐标分量m2(Bj)=0，此时m1(Ai)m2(Bj)=0，即sim(m1,m2)=0

例3 假设辨识框架Θ={a,b,c}，系统中的证据如下

m1(a)=0.01，m1(b)=0.99

m2(b)=0.99，m2(c)=0.01

计算得k=0.019 9，dBPA=0.01,均表明不存在冲突。利用(4)式计算得出sim(m1,m2)=0.999 9，表明证据m1和证据m2对{b}的支持度很大，与k，dBPA的判断一致。

例4 假设在辨识框架Θ={a,b,c,d,e,f,g}下，系统中的证据为

m1(a,b,c)=0.6,m1(Θ)=0.4

m2(a,b,c,d)=0.6,m2(Θ)=0.4

m3(e,f,g)=0.6,m3(Θ)=0.4

计算得k1,2=0.000 0,k1,3，k2,3均等于0.360 0，d1,2=0.300 0,d1,3，d2,3均为0.600 0。表明证据m1和证据m3，证据m2和证据m3的冲突程度要大于证据m1和证据m2的冲突程度。但是，由(4)式分别计算出sim(m1,m2)，sim(m1,m3)sim(m2,m3)均等于0.307 7，表明3个证据间具有相同的相似度，与实际观察到的结果不相符。

为了解决相似系数有时无法正确度量冲突的情况，引入Jaccard系数矩阵D。

将Jaccard系数矩阵引入到sim中，定义证据的冲突程度为

(5)

(5)式是为了实现证据中数据对目标辨识框架中每个目标的冲突度。

表1是将k，dBPA，1-sim，conf冲突度量值相比较。

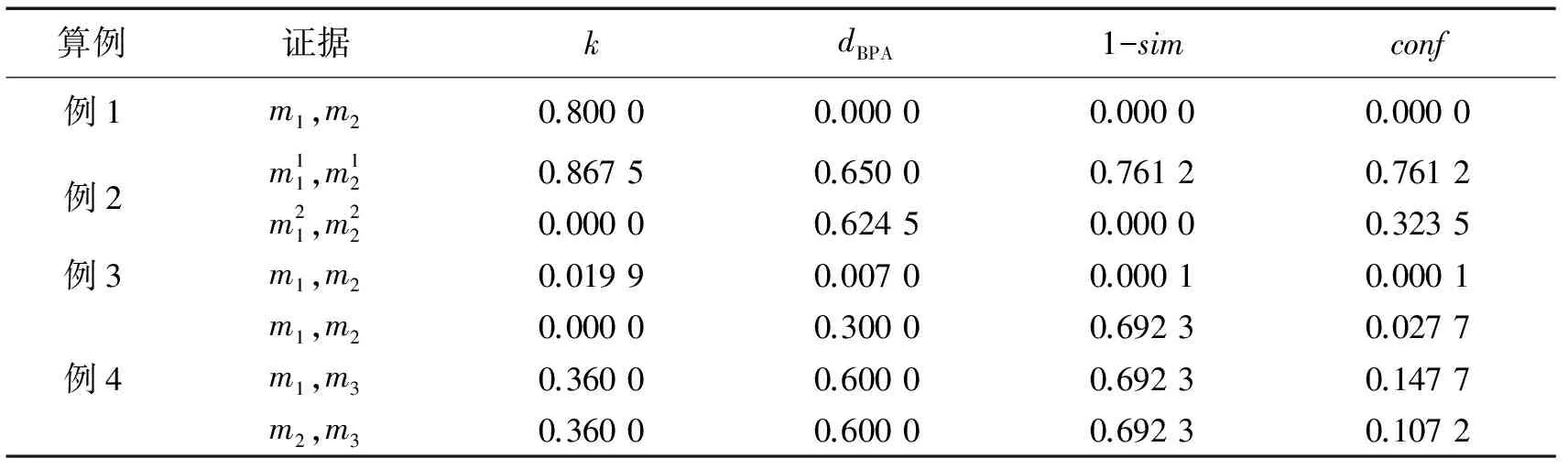
表1 4种冲突度量值

从表1可以看出:

1)例1中k=0.800 0表示证据m1和证据m2之间有冲突，此时证据m1和证据m2是2组具有相同支持度的证据，所以，用k进行冲突度量却得出与实际观察结果相悖的结论。而dBPA，1-sim，conf均为0.000 0，与实际观察到的结果相一致。

3)例3中，k，dBPA，1-sim，conf的值均小于0.019 9，表明证据m1和证据m2冲突很小。

4)例4中的conf的值均小于dBPA和k的值，表明conf比k和dBPA能够更好地度量冲突，此时的证据m1、证据m2和证据m3之间的冲突较小。

3 典型算例分析

利用文献[20]中典型的算例，分别将文献[1]中的冲突系数k，文献[5]中的关联系数r，文献[8]中的相关系数cor，文献[19]中的dBPA，文献[20]中的difBetP和本文提出的conf进行对比分析，以此来说明本文提出的度量方法也可以较好地描述证据间的冲突程度。

假设在辨识框架Θ中有20个元素，为了简化，用1,2,…,20来表示元素，即Θ={1,2,…,20}，2个基本概率赋值函数分别为m1,m2。

m1({2,3,4})=0.05,m1({7})=0.05

m1({Θ})=0.1,m1({A})=0.8

m2({1,2,3,4,5})=1

其中，子集A按照{1}，{1,2}，…，{1,2,…,20}规律变化。

表2对比了几种常见的冲突度量值。图1显示了k，dBPA，difBetP，1-r，1-cor，conf随着子集A变化的冲突度量值的变化。

由表2和图1可以看出：

1)无论子集A如何变化，冲突系数k始终为0.050 0，这不符合常理。

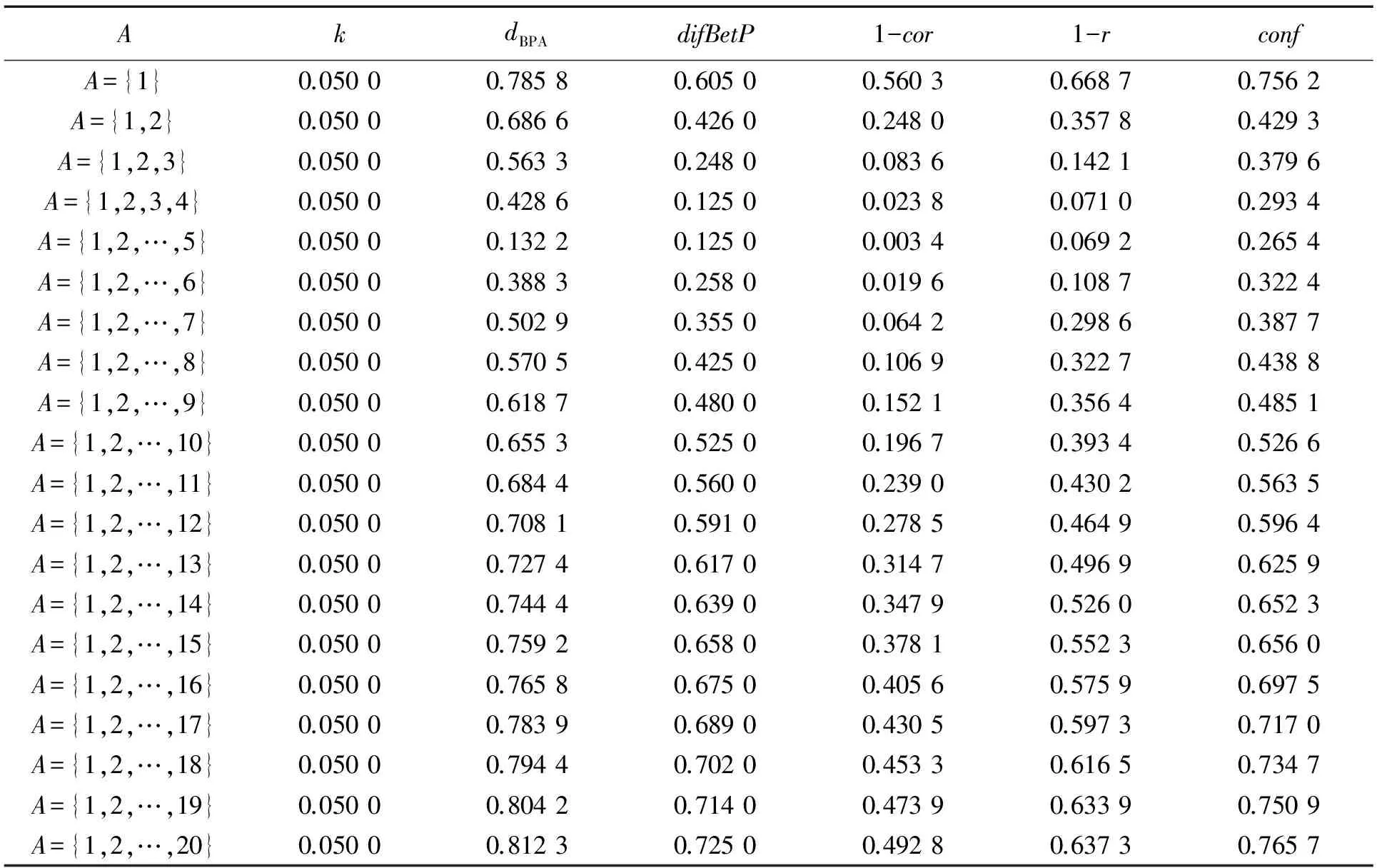
表2 6种冲突度量值的对比表

2)随着子集A的不断增加，除了k始终为一条平滑的直线外，其余的几条冲突度量值曲线的变化趋势大体一致。

3)当子集A={1,2,…,5}时，除了k曲线外，其余几条冲突度量值曲线均达到峰谷。此时表明证据m1和证据m2之间的冲突最小。

4)当子集从A={1,2,…,6}变化到A={1,2,…,20}时，dBPA，difBetP，1-r，1-cor和conf的曲线均呈上升趋势，表明证据m1和证据m2的冲突随着子集A中元素的增加而逐步增大，与直观上的分析相一致。

5)当子集A={1,2,3,4,5}时，conf=0.265 4，此时的冲突程度值最小。

如前面所述，本文提出的度量证据冲突程度的conf同dBPA，difBetP，1-r，1-cor一样均可以随着子集A的变化，反映证据之间的冲突程度，与直观上的分析相一致，同时解决了相似系数1-sim有时无法正确度量冲突的情况。所以，本文提出的基于相似系数和Jaccard系数矩阵的冲突度量方法是可行的，可以全面准确地衡量证据间的冲突程度。

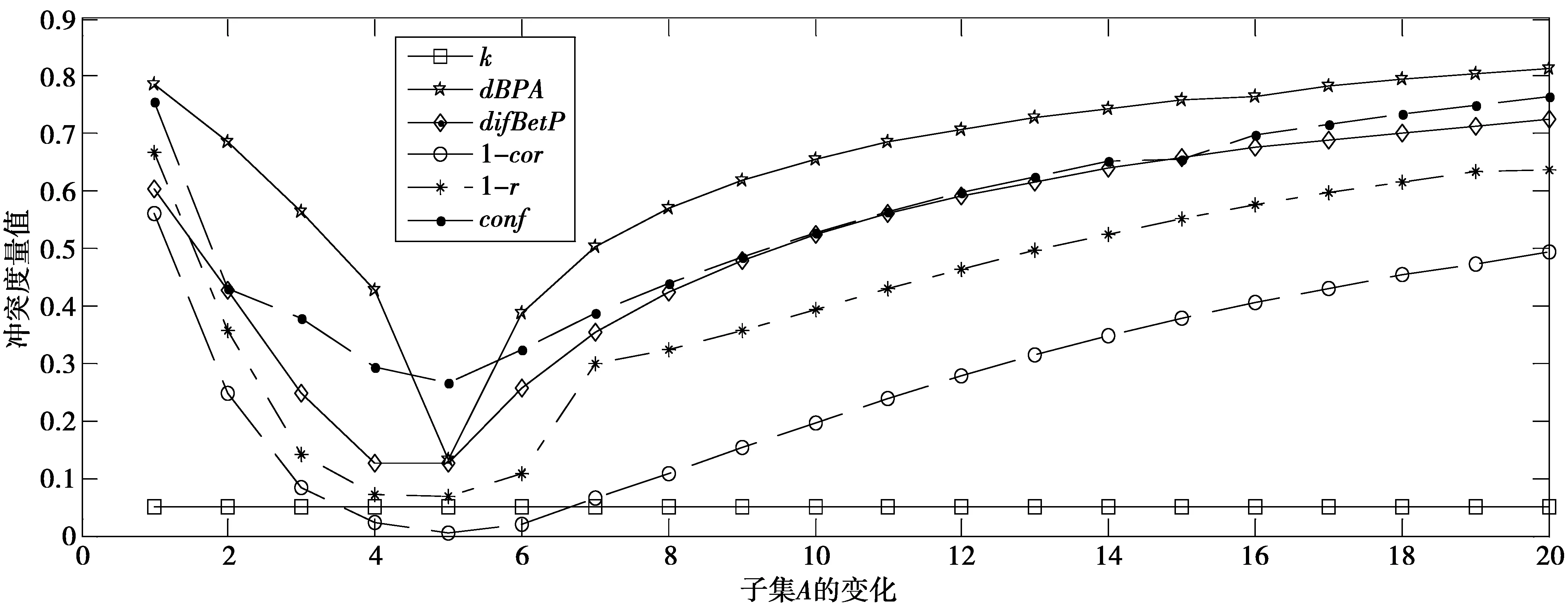
图1 6种冲突度量值随着子集A的变化对比图Fig.1 Comparison of six conflict measure values when subset A changesing

4 结束语

为了避免出现冲突误判的情况，本文首先定义了相似系数，并结合Jaccard系数矩阵来共同进行冲突的度量。通过算例分析对比本文的冲突度量方法和其他方法，结果表明该方法可以全面准确地衡量证据间的冲突程度。

但是，本文的方法是在辨识框架完整的前提下提出的，如果在开放世界的前提下，该方法是否适用值得商榷。同时，本文并未给出冲突证据的合成方法，在基于证据理论的信息融合系统中如何根据证据的冲突来选择证据组合方法则是下一步需要研究的课题。

[1] DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. The Annals of Mathematical Statistics, 1976, 38(2): 325-329.

[2] 柯小路,马荔瑶,王永.奇异值衡量证据冲突的新方法[J].电子学报, 2013, 41(10): 2109-2122. KE Xiaolu, MA Liyao, WANG Yong. A New Method to Measure Evidence Conflict Based on Singular Value[J]. Acta Electronica Sinica, 2013, 41(10): 2109-2122.

[3] 王保云,王桂林,王婷,等.基于矩阵奇异值分解的证据冲突度量算法[J].云南大学学报：自然科学版, 2014, 37(1):43-51. WANG Baoyun, WANG Guilin, WANG Ting, et al. Evidence conflict measure based on singular value decomposition of matrix[J]. Journal of Yunnan University: Natural Sciences Edition, 2014, 37(1):43-51.

[4] 邢晓辰,蔡远文,李岩,等.一种改进的证据冲突衡量因子[J]. 电讯技术, 2015, 55(11): 1225-1231. XING Xiaochen, CAI Yuanwen, LI Yan, et al. An improved measure factor of evidence conflict[J]. Telecommunication Engineering, 2015, 55(11): 1225-1231.

[5] 邓勇,王栋,李齐,等.一种新的证据冲突分析方法[J].控制理论与应用, 2011, 28(6): 839-844. DENG Yong, WANG Dong, LI Qi, et al. A new method to analyze evidence conflict[J]. Control Theory and Applications, 2011, 28(6): 839-844.

[6] MO H M, LU X, DENG Y. A generalized evidence distance[J]. Journal of Systems Engineering and Electronics, 2016, 27(2): 470-476.

[7] 蒋雯,彭进业,邓勇.一种新的证据冲突表示方法[J].系统工程与电子技术, 2010, 32(3): 562-565. JIANG Wen, PENG Jinye, DENG Yong. New representation method of evidential conflict[J]. Systems Engineering and Electronics, 2010, 32(3): 562-565.

[8] 宋亚飞,王晓丹,雷蕾,等.基于相关系数的证据冲突度量方法[J].通信学报, 2014, 35(5): 95-100. SONG Yafei, WANG Xiaodan, LEI Lei, et al. Measurement of evidence conflict based on correlation coefficient[J]. Journal on Communications, 2014, 35(5): 95-100.

[9] 李玲玲,马东娟,王成山,等.DS证据理论冲突处理新方法[J].计算机应用研究, 2011, 28(12): 4529-4531. LI Lingling, MA Dongjuan, WANG Chengshan, et al. New method for conflict evidence processing in D-S theory[J]. Application Research of Computers, 2011, 28(12):4529-4531.

[10] 王万请,赵拥军,黄洁,等.一种非对称的证据冲突度量方法[J].控制与决策, 2014, 29(3): 533-536. WANG Wanqing, ZHAO Yongjun, HUANG Jie, et al. An asymmetrical measure for evidence conflict[J]. Control and Decision, 2014, 29(3): 533-536.

[11] 彭颖,胡增辉,沈怀荣.一种修正证据距离[J].电子与信息学报, 2013, 35(7): 1624-1629. PENG Ying, HU Zenghui, SHEN Huairong. A modified distance of evidence[J]. Journal of Electronics and Information Technology, 2013, 35(7): 1624-1629.

[12] 张燕君,龙呈.一种改进的冲突表示方法[J].计算机应用研究, 2013, 30(6): 1716-1717, 1730. ZHANG Yanjun, LONG Cheng. Improved conflict representation method[J]. Application Research of Computers, 2013, 30(6): 1716-1717, 1730.

[13] 韩德强,邓勇,韩崇昭,等.利用不确定度的冲突证据组合[J].控制理论与应用, 2011, 28(6): 788-792. HAN Deqiang, DENG Yong, HAN Chongzhao, et al. Conflicting evidence combination by using uncertainty degree[J]. Control Theory and Applications, 2011, 28(6): 788-792.

[14] 胡丽芳,关欣,邓勇,等.广义幂集空间中证据冲突的原因分析[J].控制理论与应用,2011,28(12):1717-1722. HU Lifang, GUAN Xin, DENG Yong, et.al. Cause-analysis for conflicting evidences in the generalized power space[J]. Control Theory and Applications, 2011, 28(12): 1717-1722.

[15] DENG Y. Generalized evidence theory[J]. Applied Intelligence, 2015, 43(3): 530-543.

[16] 胡昌华,司小胜,周志杰,等.新的证据冲突衡量标准下的D-S改进算法[J].电子学报,2009,37(7):1578-1583.

HU Changhua, SI Xiaosheng, ZHOU Zhijie, et al. An improved D-S algorithm under the new measure criteria of evidence conflict[J]. Acta Electronica Sinica, 2009, 37(7): 1578-1583.

[17] 陈圣群,王应明.证据的分组合成方法[J].控制与决策, 2013, 28(4): 574-578. CHEN Shengqun, WANG Yingming. Grouping method for combining evidence[J]. Control and Decision, 2013, 28(4): 574-578.

[18] LIU Z G, PAN Q, DEZART J, et al. Gredal classification rule for uncertain data based on belief functions[J]. Pattern Recognition, 2014, 47(7): 2532-3541.

[19] JOUSSELME A L, GRENIER D, BOSSE E. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(1): 91-101.

[20] LIU W R. Analyzing the degree of conflict among belief functions[J]. Artificial Intelligence, 2006, 170(11): 909-924.

(编辑：张诚)

The National Natural Science Foundation of China(61102117)

Evidence conflict measurement method based on similarity coefficient and Jaccard matrix

MENG Chenchen，XIAO Jianyu，LUO lan
(School of Computer Science and Technology, Huaibei Normal University, Huaibei 235000, P.R. China)

Aiming at the open issue that the classical conflict coefficient and Jousselme distance measure can not correctly judge the conflict evidence, a new measurement of conflict was presented based on the definition of similarity coefficient and Jaccard matrix. By calculating the similarity coefficient between the evidence and the Jaccard coefficient matrix, the similarity coefficient is transformed into the conflict degree of the evidence. Theoretic proof and numreical examples verify the efficiency of the proposed measurement. A typical example is analyzed and compared with other methods. It has been shown by comparison with other methods that the proposed measurement is more accurate to measure evidence conflict.

D-S evidence theory; conflict measurement; similarity coefficient; Jaccard coefficient matrix

2016-08-01

2017-04-09 通讯作者：肖建于 xy_xiao@163.com

国家自然科学基金(61102117)

10.3979/j.issn.1673-825X.2017.03.022

TP274

1673-825X(2017)03-0421-06