基于压缩感知的塔康方位估计算法
2017-06-19姜力茹许云达
姜力茹,许云达,高 猛
(空军大连通信士官学校,辽宁 大连 116600)

基于压缩感知的塔康方位估计算法
姜力茹,许云达,高 猛
(空军大连通信士官学校,辽宁 大连 116600)
塔康(tactical air navigation,TACAN)信号峰值检测后的离散数据呈随机采样特性,为避免Kalman算法产生滤波发散问题并有效减小对数据量的需求,提出一种基于压缩感知理论的方位估计方法。通过对塔康信号的角度空间进行稀疏分解和观测值压缩,优化重构原始包络信号进而获得方位估计值。仿真实验证明了该算法的性能,与最小二乘拟合算法相比,在保证估计精度的同时进一步降低了峰值数据量,大大减少了计算过程中的冗余,并且在信噪比较大的情况下,方位估计准确度较最小二乘拟合有一定提高。
塔康(TACAN)信号;压缩感知;信号重构;方位解算;最小二乘拟合
0 引 言
塔康(tactical air navigation,TACAN) 属于近程无线电导航系统,是航空最主要的导航装备之一[1]。塔康主要由地面信标和机载设备组成,可以为飞行目标提供方位和斜距导航信息,实现极坐标定位[2]。为克服模拟体制定位精度不高、噪声容忍度低的缺陷,中频数字化技术在塔康方位估计中得到了广泛应用。其中,文献[3]提出对高速采样得到的离散脉冲幅度调制(pulse amplitude modulation, PAM)视频信号直接曲线拟合估计方位,但由于塔康视频信号占空比很大,直接拟合误差较大。在此基础上,文献[4]提出了基于Kalman滤波的塔康方位估计算法。文献[4]较文献[3]的改进之处在于将高速采样得到的离散视频信号进行峰值点估计压缩数据量,在降低峰值数据存储量的同时很大程度上剔除了不在包络上的无用点,拟合精度提高。但经过峰值检测后的离散数据呈现随机采样特性,这时采用Kalman滤波得到的状态估计可能有偏,估计的方位误差趋于无穷,导致滤波发散,估计精度严重下降。
为解决上述不足,本文提出了基于压缩感知的塔康方位估计方法。文献[5-6]于2006年提出了压缩感知(compressive sensing, CS)理论,它突破了传统奈奎斯特采样定理的限制,充分利用信号的可压缩性或在某一变换域的稀疏性来实现信号高概率重构,因此,广泛应用于雷达成像、目标跟踪等信号处理领域[7]。本文利用塔康信号在角度空间的稀疏性,通过构造冗余原子库对峰值采样点进行稀疏分解,随后利用满足受限等距性质(restricted isometry property,RIP)准则的随机矩阵对观测值进行压缩,最后通过迭代运算优化重构信号,有效避免了Kalman滤波算法发散问题,并且与文献[8]提出的最小二乘拟合算法相比,在保证塔康定位精度的同时,迭代收敛所需要的峰值数据量降低到十分之一,大大减少了拟合过程中的峰值冗余。
1 塔康信号测位原理
塔康测位分为粗测和精测2个部分。地面信标天线在水平面内以顺时针旋转的心脏形方向性图向外围空间发射频率为15 Hz的方位调制信号。以主基准信号为参考点,取正弦波的正斜率拐点为包络比相参考点,此时,比相参考点滞后于主基准的相位差就是塔康系统的粗测角[8]。为了提高测角精度,地面信标天线在粗测单一心脏形的基础上附加了九瓣调制,即机载设备接收的15 Hz包络里含有频率为135 Hz的正弦波。若测量电路测出粗测角为θ1,精测角为θ2,则飞机方位角为
(1)
2 压缩感知理论基础
压缩感知是近年来信号处理领域的热点,通过开发待观测信号在某变换域中的稀疏性,用一个与变换基不相关的观测矩阵将高维离散信号投影到低维空间,然后通过求解一个优化问题从少量随机投影中高概率完美重构信号。压缩感知主要研究内容如下。
1)信号稀疏表示。寻找一个基矩阵使得信号表示的稀疏系数尽可能少,这是信号精确重构的前提和基础[9]。
假设一个有限长、一维实值离散信号x∈RN×1,其分量为xi∈x,i=0,1,…,N-1。假设在某一变换域下,原始离散信号中的任意分量可由一组基φT=[φ1,φ2,…,φN]线性组成,则x可以表示为
(2)
(2)式中:ψ是N×N的基矩阵;s是x在ψ域内的等价向量表示。若x在基ψ上仅有K(K≪N)个非零系数si,则ψ为信号x的稀疏基,x是K稀疏的。
2)观测矩阵设计。设计一个与稀疏基不相关的观测矩阵Φ=[φ1,φ2,…,φN] 对系数向量进行线性变换得
y=Φx=Φψs=Θs
(3)
(3)式中:Θ为M×N维感知矩阵;y为M×1维压缩测量值,其中M≪N[10]。
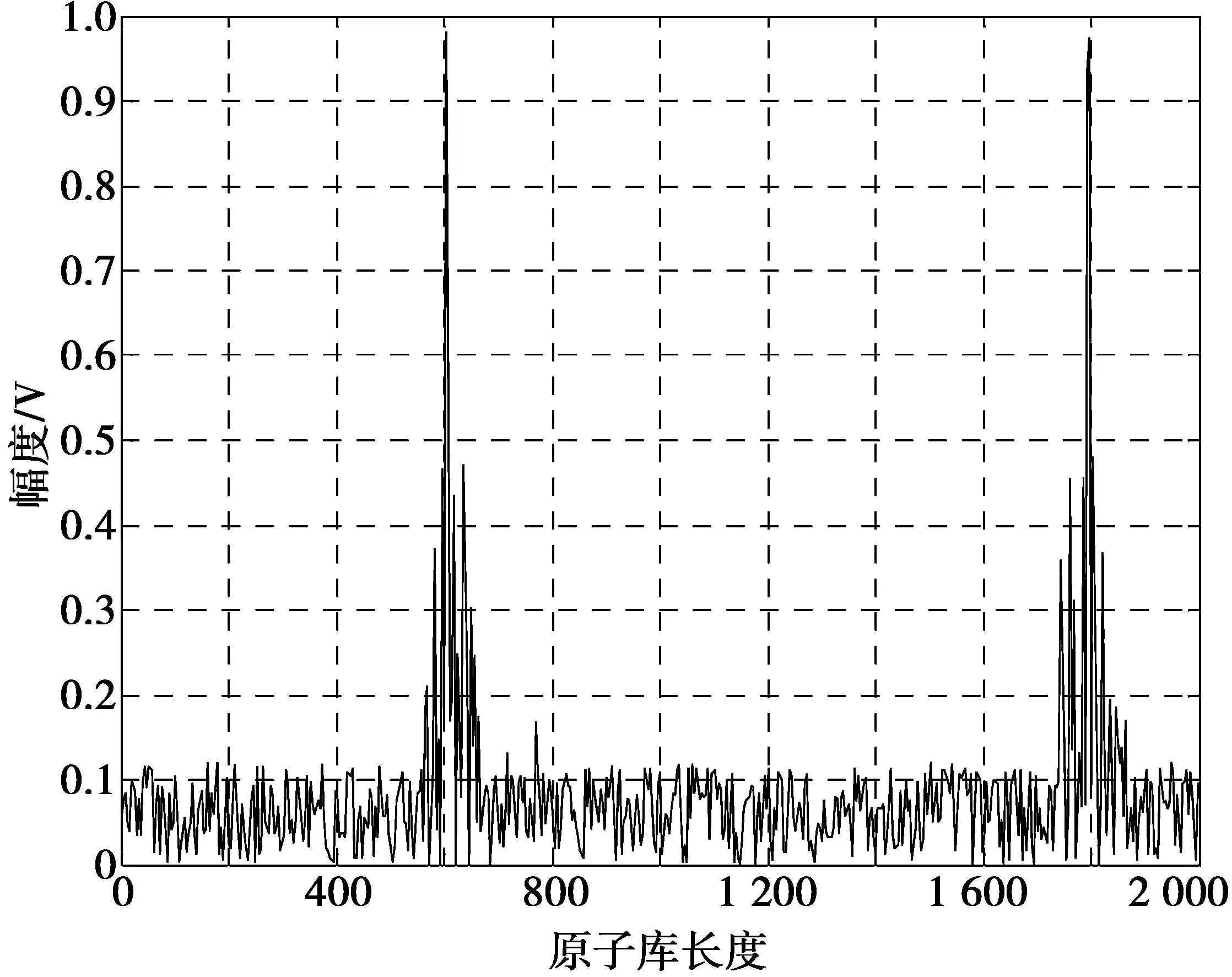
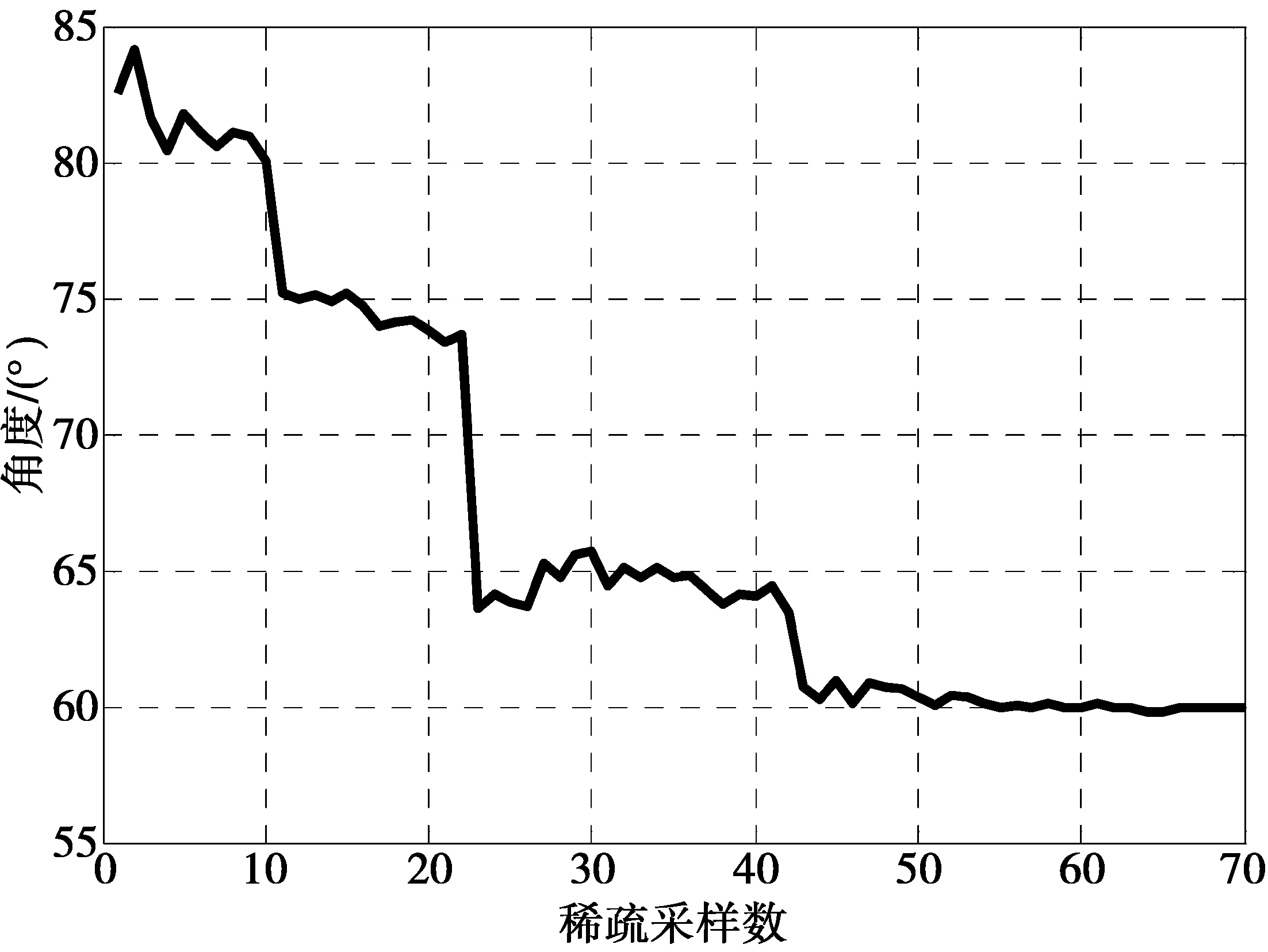
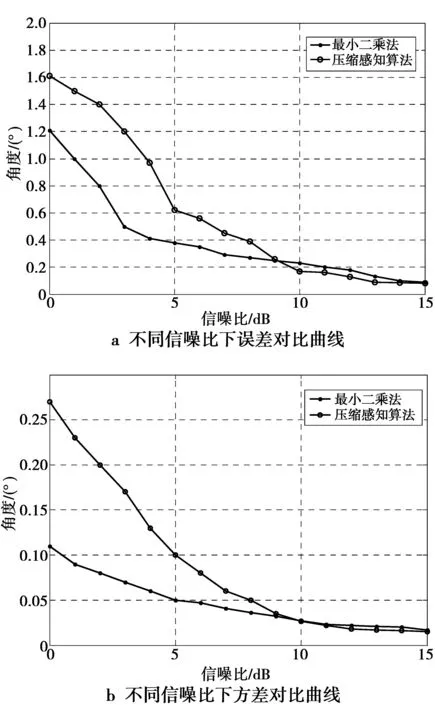
3)信号重构算法。对信号重构实际上是对(3)式求逆运算,但由于y,Θ恢复x是一个病态线性方程,可以根据K 3.1 塔康系统数学模型 由塔康系统测位原理得知以主基准为时间起点的塔康方位包络信号表示为 (4) (4)式中:Um为视频脉冲信号幅度;m1和m2分别为15 Hz和135 Hz正弦包络信号的调制度;θ1,θ2分别为飞机方位的粗测角和精确角;δ(t-ti)G(t)为特定时间点的钟形脉冲对[11]。在信标天线理想旋转频率下,f1,f2分别为15 Hz和135 Hz。 机载设备采用中频数字化技术,处理后的数字中频信号经下变频和高速采样可得离散化视频信号,表达式为 U(k)=Um[1+m1sin(2πf1kfs-θ1)+ m2sin(2πf2kfs-θ2)]· (5) (5)式中:k=1,2,…,N;fs表示信号采样频率;未知量为Um,m1,m2,θ1,θ2。 由(5)式可以看出,塔康视频信号中含有大量随机填充脉冲,在中频数字化塔康系统中一般以主基准脉冲群的第10对脉冲到达时间作为周期起点,每个周期约3 000对脉冲。在无噪声情况下,对离散化的视频信号进行峰值检测能获得约6 000个非均匀分布峰值,峰值点方程可表示为 (6) 部分峰值点组成的塔康包络信号如图1所示。 图1 部分峰值点检测图Fig.1 Part of the peak point detection 3.2 角度空间稀疏表示 在对离散视频信号进行方位估计时,构造θ1,θ2目标未知量的稀疏域是压缩感知的关键。对于塔康信号,需要估计粗测角θ1和精测角θ2这2个未知量,由此可以构造稀疏度K为2的角度空间。由于塔康信号是15 Hz,135 Hz正弦波与脉冲信号的混合信号,采用单一正交基无法将待估计量θ1,θ2分离出来,故考虑通过设计冗余原子库取代规范正交基函数实现角度空间稀疏表示。 基于(6)式,峰值点方程可简化成2部分,表示为 (7) S1(kj)=A1{exp[w1fskj-θ1]-exp[w1fskj+θ1]} (8) S2(kj)=A2{exp[w2fskj-θ2]-exp[w2fskj+θ2]} (9) 针对S1(k)和S2(k)分别构造原子库的原子,对于S1(k),有 gr=exp[w1fskj-θl]-exp[w1fskj+θl] (10) 设θl为要估计的粗测方位角,为便于研究,将θl取值为θl∈[0°,180°],l=1,2,…,L,L为待估粗测角个数,kj代表第j个采样点,原子参数组可以表示为r=(θl,kj),则信号S1(k)可构造原子库 (11) U=Gs+n (12) (12)式中,s表示塔康信号在角度域的幅度,且s中只有K个非零值,即实现了角度空间稀疏化。 由(3)式M×1维压缩测量值y重构信号,感知矩阵Θ必须满足RIP:对于所有K—稀疏的向量x∈Rn,满足 (13) 即说明采样所得少量观测值包含了足够恢复原始信号的全部信息。 由文献[12]得知,高斯随机测量矩阵能以高概率与任意稀疏基ψ不相关,使得在M满足的条件下,Θ符合RIP性质。因此,本算法构造M×N高斯随机矩阵,并对每一列进行归一化处理得到测量矩阵Φ。此时,观测峰值数据U经过压缩后M×1维测量值y可以表示为 y=ΦU=ΦGs+Φn (14) ‖s‖1, s.t. ‖y-Θs‖<ε (15) 3.3 塔康信号重构 信号在过完备集上的最优稀疏分解是一个非确定多项式(non-deterministic polynomial,NP)问题。为此,可以转而寻找求次最优解。但为了克服基本匹配追踪算法中新得到的原子和前面已得到原子张成的子空间不正交,影响迭代和收敛速度的问题,本文采用改进算法—正交匹配追踪算法(orthogonal matching pursuit, OMP)[13]。算法重构步骤如下。 步骤1 初始化残余分量r0=y,迭代次数p=1,索引值集合Λ=∅,J=∅。 步骤2 挑选索引,计算余量与等效测量矩阵Θ内积的绝对值,从中找出相关度最高的原子,其满足 步骤3 更新索引集合Λp=Λp-1∪{λp},此时,搜索得到的原子构成的原子集合为qp=[qp-1qλp]。 步骤5 如果‖rp-r‖≥ε,则r=rp,并且令p=p+1,转步骤2,否则迭代结束。 采用Matlab软件仿真平台对本文算法的精确性和稳定性进行实验,并对结果进行分析。理想发射频率下塔康信号参数设置如表1所示。 表1 塔康信号参数表 实验1 为了验证本文所提算法的有效性,利用图1搜索出的部分峰值数据重构塔康信号并进行方位估计。本实验中信噪比SNR=10 dB,压缩测量值M=50,仿真结果如图2和图3所示。 图2 恢复包络与真实包络对比图Fig.2 Contrast figure of return envelope and real envelope 图3 塔康方位估计图Fig.3 Figure of TACAN azimuth estimation 从图3的结果可以看出,在角度稀疏空间中存在2个归一化峰值点。搜索离散幅度值中2个最高点对应的原子库长度分别与搜索步长相乘得到塔康粗测角和精测角。由图3可以计算得出,此时,塔康方位粗测角为60.1°,精测角为178.8°,估计误差不超过0.5°,达到塔康高精度测角要求。 实验2 为了考查本文算法收敛性,在SNR=10 dB下,对不同稀疏采样数据量情况下的塔康方位估计准确度进行仿真,仿真结果如图4所示。 图4 压缩感知算法收敛曲线图Fig.4 Convergence curve of compressed sensing algorithm 由图4可以看出,在稀疏采样点数满足一定值的条件下,压缩感知算法估计精度可以满足测角要求。随着稀疏采样点数不断增加,方位估计误差逐渐减小,当采样点数达到48时,曲线走势基本稳定,算法趋于收敛。同时,由文献[8]仿真结果可知,最小二乘拟合在峰值点数为400左右时算法收敛,本文算法需要的稀疏采样数与最小二乘算法收敛时的峰值数据量之比为η=0.1,数据降低到十分之一,大大减少了计算过程中的峰值冗余。 实验3 为了验证不同信噪比环境下该算法的方位估计性能,采用与最小二乘估计算法对比的形式,利用Monte Carlo仿真方法,对同一塔康离散视频信号进行方位估计。定义方位估计方差为 (16) 实验结果如图5和图6所示。 由图5可知,随着信噪比不断增加,2种方法估计出来的方位值误差和方差都减少。但在低信噪比情况下,利用最小二乘算法进行方位估计精度优于压缩感知算法,此时,压缩感知算法受噪声影响敏感,误差和方差曲线走势陡峭,但大致趋势仍能够满足塔康系统精度为2°的要求。随着信噪比提高,压缩感知算法精度上升明显,估计性能逐渐趋于平稳。图6仿真结果显示,当SNR=10 dB时,本文所提算法抖动概率变小,估计精度较最小二乘算法有一定提高。 图5 不同功率信噪比下对比曲线Fig.5 Contrast curve of different signal noise ratio 图6 10 dB时方位估计对比图Fig.6 Contrast figure of azimuth estimation under 10 dB 本文考虑到塔康系统方位估计中采用的Kalman滤波算法发散问题严重,最小二乘拟合算法所需峰值点数目过多的问题,提出了基于压缩感知的塔康方位估计算法。该算法将压缩感知理论融入到塔康方位解算过程中,在角度稀疏空间中仅需少量稀疏峰值采样点即可高概率恢复出塔康信号,同时仿真结果表明,在信噪比较大的情况下,该算法方位估计精度略高于最小二乘估计。 [1] SHEST L N. A cylindrical array for the TACAN system [J].IEEE trans antennas propagation, 1974, 22(01): 17-25. [2] CHRESTOPHER E J. Electronically scanned TACAN an-tenna[J].IEEE Transactions on Antennas Propagation, 1974,26(01): 12-16. [3] 王维康, 张斌, 李睿,等. 塔康系统输出参数的精确测量方法[J]. 电光与控制,2010, 17(07):78-83. WANG Weikang, ZHANG Bin, LI Rui, et al. Accurate Measurement of TACAN Output Parameters[J]. Electronics Optics and Control,2010, 17(07):78-83. [4] 张国祥, 郭英, 霍文俊,等. 基于Kalman滤波的塔康方位精确解算方法 [J]. 空军工程大学学报:自然科学版,2013, 12(02): 76-80. ZHANG Guoxiang, GUO Ying, HUO Wenjun, et al. Accurate Calculating Method of TACAN Bearing Signal Based on Kalman Filtering[J]. Journal of air force engineering university: Natural Science Edition,2013, 12(02): 76-80. [5] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(04):1289-1306. [6] CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies[J].IEEE Transactions on Information Theory,2006, 52(12):5406-5425. [7] 王海涛, 王俊. 基于压缩感知的无源雷达超分辨DOA估计[J]. 电子与信息学报,2013, 35(04):878-881. WANG Haitao, WANG Jun. Super-resolution DOA Estimation in Passive Radar Based on Compressed Sensing[J]. Journal of Electronics and Information Technology,2013, 35(04): 878-881. [8] 陈坤, 田孝华, 赵颖辉. 基于最小二乘迭代算法精确估计塔康方位参数[J]. 科学技术与工程,2013, 13(15):4176-4180. CHEN Kun, TIAN Xiaohua, ZHAO Yinghui.Accurate Estimation for TACAN Azimuth Based on Iterative Least Square Algorithm[J].Science Technology and Engineering,2013, 13(15):4176-4180. [9] 吴仁彪, 韩雁飞, 李海. 基于压缩感知的低空风切变风速估计方法[J]. 电子与信息学报,2013, 25(10): 2512-2517. WU Renbiao, HAN Yanfei, LI Hai, et al. Wind Speed Estimation for Low-attitude Wind Shear via Compressive Sensing[J]. Journal of Electronics and Information Technology,2013, 25(10): 2512-2517. [10] 张硕,王杰,王金成,等.基于压缩感知的三维物体成像的简单计算方法[J].光学学报,2013,33(01):1-7. ZHANG Shuo, WANG Jie, WANG Jincheng, et al. Simple Calculation Method for Three-Dimensional Imaging Based on Compressed Sensing[J]. Acta Optica Sinica,2013, 33(01):1-7. [11] 陈坤, 田孝华, 何晶,等. 一种基于Huber函数的塔康方位稳健估计算法[J]. 空军工程大学学报:自然科学版,2014, 14(06): 18-22. CHEN Kun, TIAN Xiaohua, HE Jin,et al. A Robust Estimation Algorithm of TACAN Azimuth Based on Huber Function[J].Journal of air force engineering university: Natural Science Edition,2014, 14(06): 18-22. [12] 周灿梅. 基于压缩感知的信号重建算法研究[D].北京:北京交通大学,2010. ZHOU Canmei. Research on Signal Reconstruction Algorithms Based on Compressed Sensing[D].Beijing:Beijing Jiaotong University,2010. [13] 郭金库, 刘光斌, 余志勇,等. 信号稀疏表示理论及其应用[M].北京:科学出版社,2013:25-27. GUO Jinku,LIU Guangbin,YU Zhiyong,et al.Signal Sparse Representation Theory and Application[M].Beijing:Science Press,2013:25-27. (编辑:王敏琦) DOI:10.3979/j.issn.1673-825X.2017.03.014 Abstract: The high efficient lossless compression of videos and images has important application value in the transmission of massive aerial and remote sensing image, the storage of precious cultural relics, and so on. However, the current researches mainly focus on lossy compression. So, according to the analysis and research of the existing lossless compression methods, a new method for lossless image compression based on the combination of sparse coding and binary neural networks is proposed. Firstly, a redundant dictionary is constructed by using the linear separable structure of the binary neural networks to obtain efficient sparse decomposition. Then the binary neural network learning algorithm is used to map the image into a binary neural network with linear separable structure. Based on this, the corresponding pattern matching algorithm is constructed to map each neuron to the redundant dictionary resume. Also the coding of the original image is established by the sparse coefficients. Finally, the lossless compression of the image is realized. The theoretical analysis shows that this method can effectively improve the compression ratio. Experiments verify the validity and generality of the algorithm. Keywords:lossless compression, binary neural network, linearly separable structure, redundant dictionary, compression ratio The National Natural Science Foundation of China(61273049) TACAN azimuth estimation algorithm based on compressed sensing JIANG Liru, XU Yunda, GAO Meng Discrete data of tractial air navigation(TACAN) signal peak detection is of random sampling. In this paper, In order to avoid filtering divergence of Kalman algorithm and effectively reduce the demand for data, a novel method of TACAN azimuth estimation is proposed based on compressed sensing theory. By performing sparse decomposition and observation compression of TACAN angel space, the original envelope signal is reconfigured for optimization, and then the reconstruction algorithm is used to recover the original signal and acquire the azimuth estimation. Experimental results show the performance of this proposed method. Compared with the other algorithm least square fitting,the method reduces peak data amount while ensuring estimation precision, which reduces the computation redundancy dramatically. Besides, in the case of large signal noise ratio (SNR), this method shows better performance of accuracy than the least square method. tactical air navigation(TACAN) signal; compressed sensing; signal reconstruction; azimuth calculation; least square fitting A novel lossless image compression scheme based on binary neural networks with sparse coding WANG Zuocheng1,2, YANG Juan3, XUE Lixia3 (1. The 38thResearch Institute of China Electronics Technology Group Corporation,HeFei,230088,P. R.China;2. AnHui Sun Create Electronic CO., LTD. HeFei, 230088,P. R.China; 3. School of Computer and Information, Hefei University of Technology, Hefei 230009, P. R.China) TP391 Document code:A 1673-825X(2017)03-0371-06 2015-05-18 2017-02-24 通讯作者:姜力茹 jiangliru9104@163.com 国家自然科学基金(61273049) 10.3979/j.issn.1673-825X.2017.03.013 TN965 A 1673-825X(2017)03-0365-06 姜力茹(1991-),女,山东烟台人,硕士研究生,主要研究方向为军用无线电导航、导航信号处理。E-mail:jiangliru9104@163.com。3 基于压缩感知的塔康方位估计算法

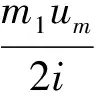




4 仿真验证与分析





5 结 论

(Dalian Air force Communication NCO Academy,Dalian 116600,P.R. China)
