基于二进制粒子群算法的OFDM稀疏信道导频优化

2017-06-19刘远航刘晓彤万晋京

重庆邮电大学学报(自然科学版) 2017年3期

关键词：导频二进制载波

刘远航，刘晓彤，彭帅，万晋京

(重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

基于二进制粒子群算法的OFDM稀疏信道导频优化

刘远航，刘晓彤，彭帅，万晋京

(重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

在正交频分复用(orthogonal frequency division multiplexing，OFDM)稀疏信道中，合理的导频设计可以提高信道估计的性能，以测量矩阵的互相关最小化作为目标，提出一种基于二进制粒子群算法的导频优化方案，引入混沌初始化机制来保证初始粒子均匀地分散在解空间里，通过粒子变异机制来保证种群的快速收敛。根据实验和仿真结果可以看出，与随机搜索导频优化算法、逐位置导频优化算法以及最小二乘法相比，该算法能够有效节省导频的开销，提高频谱利用率，具有更好的信道估计性能。

正交频分复用(OFDM)；压缩感知；导频优化；二进制粒子群算法

0 引言

正交频分复用(orthogonal frequency division multiplexing，OFDM)技术具有良好的抗频率选择性衰落和较高的频带利用率，目前已经被广泛应用于广播式的音频和视频领域以及民用通信系统等领域。OFDM技术是当今无线通信中的重要技术之一，在OFDM技术进行实现时，信道估计是进行相关检测、解调、均衡的基础[1]。信道估计质量对整个通信系统的性能起重要作用[2]。

目前最常用的信道估计方法是基于导频的信道估计方法[3]，基于导频的信道估计方法主要有最小二乘法(least squares，LS)和线性最小均方误差法(linear minimum mean square error，LMMSE)。但是这些传统的信道估计方法适应于稠密信道的信道估计。研究表明，无线信道往往呈现稀疏性[4]。对于稀疏信道，这些传统的信道估计的性能与准确度不够高。压缩感知( compressive sensing，CS )理论[5-6]展示了一种全新的信号采集处理方法，对可压缩的稀疏信号以远低于奈奎斯特速率的方式进行采样，仍能够精确地恢复出原始信号[7]。近年来的研究发现，基于压缩感知的信道估计可以利用无线信道的稀疏性，提高信道估计性能。

全球无线通信市场的猛增对日益紧缺的频谱资源的需求逐渐增大。合理设计导频放置方式不仅可以提高信道估计性能，而且能够有效节省所需导频符号，从而具有更高的频带利用率。传统的信道估计的导频结构有块状、梳状和格状。研究发现，传统的LS算法采用均匀的梳状导频结构时可以获得最佳的信道估计性能[8]。基于压缩感知的信道估计算法，具有比传统信道估计更好的性能。需要设计一种合适的导频优化方案，得到最佳的导频放置方式，才能使得基于压缩感知的信道估计性能更好。Candes和Tao[9]提出若测量矩阵满足受限等距性质准则，就可以使得接收端以比较高的概率重建出信号，然后在现实中测量矩阵是否满足有限等距性质(restrict isometry property, RIP)条件的验证具有一定的难度。文献[10]提出测量矩阵互相关值最小准则，该准则提出随着测量矩阵的互相关值变小，稀疏信号的重构精度越高。文献[11]提出了一种随机导频优化方案，该方案与传统的等间隔导频设计方案相比，具有更好的效果；文献[12]提出了一种反馈型的导频优化算法，该优化方法有效降低干扰和噪声对信道估计的影响，提高了信道估计性能；文献[13]提出了一种交叉熵优化的算法，该算法不仅减少了计算复杂度，而且在一定程度上提高稀疏信道估计的准确性；文献[14]提出了一种遗传算法的导频优化方案，该方案与随机导频方案相比，运算复杂度比较高；文献[15]提出了一种逐位置导频优化方案。该方法通过灵活的内外循环设置，具有很好的有效性。本文以测量矩阵的互相关最小化为优化目标,提出了一种基于二进制粒子群算法的导频优化方案。

1 OFDM系统的导频设计

OFDM系统框图如图1所示。

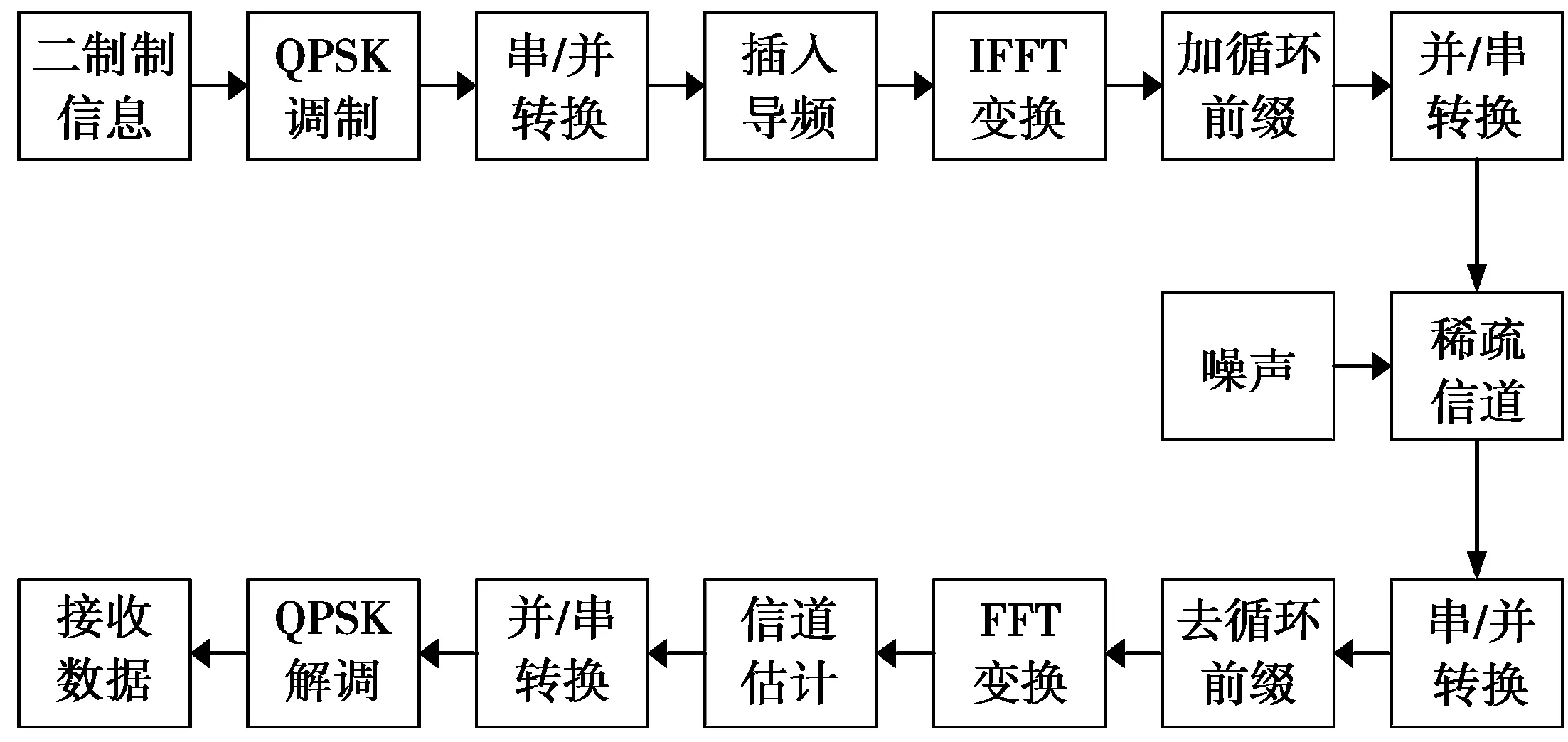
图1 OFDM系统框图Fig.1 Diagram of OFDM system

假设OFDM系统中有N个子载波,所有子载波的构成的集合为c={c1,c2,c3,…,cN}，N×1维的接收端的信号可以表示为

y=XH+W=XFh+W

(1)

(1)式中：N×N维矩阵X可以表示为X=diag(x(0),x(1),x(2),x(3),…,x(N-1))；h=[h0,h1,h2,…,hL-1]，h为信道的离散时域冲激响应；H为对应的频域响应；F为N×L维矩阵；W为N×1维向量的高斯白噪声。

当信道的相干时间远大于OFDM符号持续时间时，在一个OFDM符号中的信道参数可以认为是不变的，信道的冲击响应可以表示为

(2)

(2)式中：L为OFDM信道模型中抽头延时的总个数；hi为第i个抽头的复增益，该信道的稀疏性主要表现在[h0,h1,h2,…,hL-1]中数值比较大的几个相对较少的元素或非零元素的个数；τi为第i个抽头的延时；σ(t-τi)为第i个抽头的冲击信号。

从c中的N个子载波中选择出P个子载波用于发送导频符号，则导频子载波构成的信号cp={cN1,cN2,cN3,…,cNp}。设P×N维的选择性矩阵S，P个导频信号处在接收端收到的对应信号则可以表示为

(3)

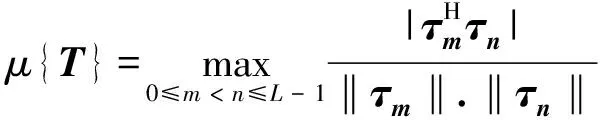
(4)

(4)式中：P表示导频总数；ci表示从N个子载波中选择出的第i个子载波用于发送导频符号；‖Xi‖2表示第i个导频对应的信号的功率。其中，影响矩阵XP×PFP×L取值的共有2个因素：①导频符号在子载波中的位置；②导频符号的信号功率；假定所有的导频符号的信号功率都相同，且都等于1，则

(5)

此时，μ{T}的大小只与导频的位置有关，如何从N个子载波中选择出P个子载波作为导频进行传输，使得μ{T}最小，设a=n-m，μ{T}用目标函数f(p)表示，则

(6)

2 基于二进制粒子群算法的导频优化算法

本文采用基于二进制粒子群算法的导频优化方案。问题已经转化为如何从N个子载波中选择出P个子载波作为导频，使得测量矩阵的互相关值μ{T}最小。通过二进制编码的形式来表示子载波，用来传送导频的子载波用数值“1”表示，用来传送数据的子载波用数值“0”表示。

本项目在现有激光焊接装配技术的基础上开发了新型多功能激光焊接试验平台，用于激光焊接设备日常焊接工艺试验。焊接试验平台在满足现车手动压紧和气缸自动压紧功能的基础上完成电磁吸附压紧功能开发，并进行激光焊接试验，分析了电磁场对激光焊缝的影响，研究电磁吸附式工装用于奥氏体不锈钢车体激光焊接的可行性。

Kennedy和Eberhart[16]提出二进制粒子群(binary particle swarm optimization，BPSO)算法，该算法中的每个粒子都由二进制编码表示。速度则决定粒子位置在[0,1]区间上的转变概率参数，该参数的取值就是位变量取数值“1”的概率。为了将速度的值映射到[0,1]区间，引入了函数即sig函数，表示为

(7)

BPSO中粒子的位置和速度更新可以表示为

(8)

(9)

直接运用二进制粒子群算法进行导频设计的缺点是该算法的收敛比较慢。因此，引入了一种粒子的变异机制。当每一代的粒子群经过粒子位置更新之后。这一代粒子群中若发现某个粒子的取值为数值“1”的维数之和Q大于规定的导频个数P时，则对该粒子进行变异，变异的机制是，从该粒子的Q维取值为数值“1”的元素中随机选取Q-P维元素，将其数值都突变为数值“0”。则突变后的该粒子取值为数值“1”的维数之和变为P。

粒子群算法的初始化会对算法的性能产生一定的影响。因此，在初始化过程中要尽量使得粒子均匀的分散在解空间里。混沌序列间具有遍历性和随机性，可以保证种群在解空间里均匀的分布。因此，选用混沌初始化方法。本文利用Logistic映射的方法，公式为

zk+1=μzk(1-zk)

(10)

(10)式中：zk是Logistic映射的的混沌变量；μ是混沌因子，本文中μ=4。

利用BPSO进行导频设计的主要步骤如下。

步骤4 利用(6)式求的粒子的适应度，并且根据适应度计算出粒子群的个体最优值和全局最优值。

步骤5 对粒子的速度和位置进行更新，通过引入映射函数，即sig函数，则粒子的位置和速度更新可以用(8)式和(9)式表示。

步骤7 若到达设定的迭代次数，停止迭代,否则返回步骤4继续进行迭代。

3 仿真与性能分析

为了验证提出的算法的有效性，本文进行了如下的仿真，仿真参数如表1所示。

表1 仿真参数设置表

在仿真的过程中，多径信道模型中各径时延在(0，τmax)上随机分布，τmax为最大路径时延，路径增益服从复高斯分布，且路径复增益的功率随路径时延的增大以指数函数exp(-τi/τmax)衰落。对二进制粒子群算法的参数取值为：种群的规模size=500，最大的迭代次数iterator=150。粒子的维数等于子载波总数N，惯性权重w=1，学习因子c1=c2=10。仿真计算机的配置为，AMD四核主频为3.22 GHz的处理器，操作系统为微软windows7，内存为4 GByte，用MATLAB R2012a软件进行仿真。

二进制粒子群算法大约在运行500 s之后，即迭代100次之后基本上达到稳定。在文献[11]提出了一种随机的导频搜索算法，本文简称该算法为随机搜索导频优化方案，求得测量矩阵的互相关最小值。在文献[15]中提出了一种通过灵活设置内、外循环，提出了对导频序列逐位置替换与优化的方法。每次执行外循环都形成一种随机的导频序列，内循环实现导频序列的逐位置优化过程，本文简称该算法为逐位置导频优化方案。本文与文献[11，15]算法进行对比，得到两者运行时间对应的测量矩阵的互相关最小值。3种导频优化算法运行时间的对比如图2所示，通过对比发现，当运行时间不小于200 s时，二进制粒子群算法相比于随机导频算法以及逐位置导频优化算法，能够得到更小的目标函数值。为了突出对比，通过对传统的LS的信道估计进行对比，由于LS信道估计的最优导频设计方式是等间隔的均匀导频间隔[17]。因此，传统的LS信道估计采用等间隔的均匀导频方式。基于压缩感知的信道估计分别采用文献[11]的随机导频放置方式，文献[15]提出逐位置优化方案产生的导频放置方式以及本文所提出的基于二进制粒子群算法的导频放置方式，分别都取运行500 s时，得到的互相关值对应的导频。采用随机搜索导频优化对应的μ=0.333 0，对应的选取的导频为[12,57,63,79,100,119,126,135,147,242,275,310,371,410,492,499]，采用逐位置导频优化方案对应的μ=0.302 4，对应选取的导频是[33,60,78,129,138,159,166,201,240,252,260,360,389,404,411,477]。而采用二进制粒子群算法对应的μ=0.286 3，对应的选取的导频为[6,24,32,39,90,110,117,138,250,271,283,323,413,449,476,506]，基于压缩感知的信道估计运用OMP算法进行信道估计。

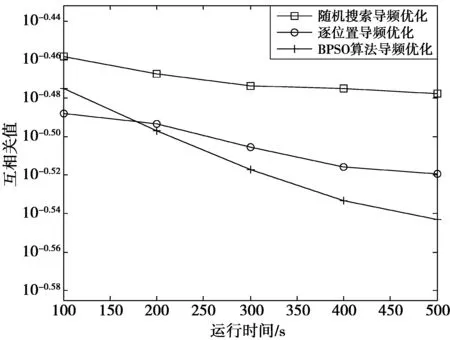
图2 3种导频优化算法运行时间的对比图Fig.2 Comparison of three algorithms operation time

LS信道估计和基于压缩感知信道估计的均方误差和误码率对比曲线如图3和图4所示，LS信道估计分别采用16导频和65导频。

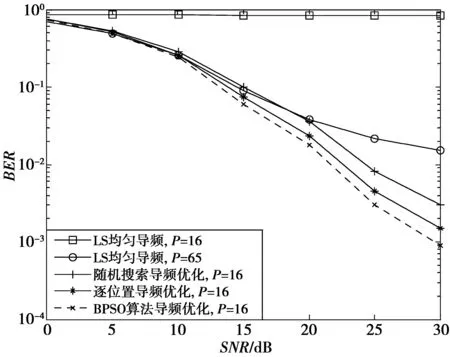
图3 误码率性能比较Fig.3 Comparison of BER performance

图4 均方误差性能比较Fig.4 Comparison of MSE performance

通过对信道估计的误码率和均方误差相比，发现当导频是16时，LS算法几乎不能正确地进行信道估计。当LS算法的导频数是65时，LS算法的信道估计性能略差于二进制粒子群算法。而在导频数目相同时，二进制粒子群算法的导频优化算法要优于LS算法、随机导频以及逐位置导频算法。由图3可得，在误码率为0.003时情况下，二进制粒子群算法的导频比随机导频算法节省大约6 dB的信噪比，比逐位置导频算法节省大约2 dB的信噪比。二进制粒子群算法的信道估计性能要略优于65导频的LS信道估计算法，二进制粒子群算法比LS算法节省大约75.4%的导频，提高了9.6%的系统频谱利用率。

4 结束语

本文在基于压缩感知的OFDM稀疏信道估计中的导频优化中，以测量矩阵的最小互相关值为优化目标，提出了一种基于二进制粒子群算法，从而求出最优导频。通过与传统的LS、随机导频算法以及逐位置导频算法进行对比，本文提出算法能够改善信道估计的性能，明显节省了导频，具有较高的频谱利用率。

[1] 姚志强, 李广龙, 王仕果, 等. 基于 Golay 互补序列的压缩感知稀疏信道估计算法 [J]. 电子与信息学报, 2015, 38(2): 282-287. YAO Zhiqiang,LI Guanglong,WANG Shiguo,et al.Compressed Sensing Channel Estimation Algorithm Based on Deterministic Sensing with Golay Complementary Sequences[J].Journal of Electronics & Information Technology,2015, 38(2): 282-287.

[2] 彭钰, 侯晓赟, 魏浩. 压缩感知时频双选信道估计 [J].信号处理, 2014, 30(1): 119-126. PENG Yu, HOU Xiaoyun, WEI Hao. Domain-Doppler Doubly Selective Channel Estimation Using Compressed Sensing [J]. Journal of Signal Processing, 2014, 30(1): 119-126.

[3] TONG L, SADLER B M, DONG M. Pilot-assisted wireless transmissions: general model, design criteria, and signal processing[J]. IEEE Signal Processing Magazine, 2004, 21(6): 12-25.

[4] 何雪云, 宋荣方, 周克琴. 基于压缩感知的 OFDM 系统稀疏信道估计新方法研究[J].南京邮电大学学报：自然科学版, 2010, 30(2):60-65. HE Xueyun, SONG Rongfang, ZHOU Keqin. Study of compressive sensing based sparse channel estimation in OFDM systems[J]. Journal of Nanjing University of Posts and Telecommunications：Natural Science Edition, 2010, 30(2): 60-65.

[5] CANDèS E J, WAKIN M B. An introduction to compressive sampling[J].IEEE signal processing magazine, 2008, 25(2): 21-30.

[6] CANDèS E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[7] DAVENPORT M A, BOUFOUNOS P T,WAKIN M B, et al. Signal processing with compressive measurements[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 445-460.

[8] 王德胜, 朱光喜, 林宏志. MIMO-OFDM最优导频设置与优化的信道估计方法 [J]. 通信学报，2005，26(1): 34-39. WANG Desheng, ZHU Guagxi, LIN Hongzhi. Optimal pilots and channel estimation in MINO-OFDM system [J]. Journal on communications, 2005, 26(1): 34-39.

[9] BERGER C R, WANG Z, HUANG J, et al. Application of compressive sensing to sparse channel estimation[J]. IEEE Communications Magazine,2010,48(11):164-174.

[10] PAKROOH P, AMINI A, MARVASTI F. OFDM pilot allocation for sparse channel estimation[J]. EURASIP Journal on Advances in Signal Processing, 2012, 2012(1): 1-9.

[11] 何雪云, 宋荣方, 周克琴.基于压缩感知的OFDM稀疏信道估计导频图案设计[J].南京邮电大学学报：自然科学版. 2011, 31(5): 7-11. HE Xueyun, SONG Rongfang, ZHOU Keqin. Design of Pilot Pattern for Compressive Sensing Based Sparse Channel Estimation in OFDM Systems[J].Journal of Nanjing University of Posts and Telecommunications：Natural Science Edition, 2011, 31(5): 7-11.

[12] 任腾飞, 李艳萍, 郝喜国.OFDM 系统中最优导频序列的设计方案[J].科学技术与工程,2015, 35(29): 148-152. REN Tengfei，LI Yanping，HAO Xiguo. Optimized Pilot Design Schemes in OFDM Systems [J]. Science Technology and Engineering, 2015, 35(29): 148-152.

[13] CHEN J C, WEN C K, TING P. An efficient pilot design scheme for sparse channel estimation in OFDM systems[J].IEEE Communications Letters, 2013, 17(7): 1352-1355.

[14] 韦世红, 孟婷婷, 唐宏.基于遗传算法的短波 OFDM信道估计导频优化方案[J]. 电视技术, 2015, 39(19): 47-50. WEI Shihong，MENG Tingting，TANG Hong. Genetic Algorithms Based Optimization Scheme of Pilot Pattern for HF Channel Estimation in OFDM System[J].Video Engineering,2015, 39(19): 47-50.

[15] 戚晨皓, 吴乐南, 朱鹏程. 认知无线电中的稀疏信道估计与导频优化[J].电子与信息学报,2014,36 (4):763-768. QI Chenhao, WU Lenan, ZHU Pengcheng. Sparse channel estimation and pilot optimization for cognitive radio [J].Journal of Electronics & Information Technology, 2014, 36(4):763-768

[16] KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm[C]//IEEE.Systems, Man, and Cybernetics, Computational Cybernetics and Simulation,1997 IEEE International Conference on.New York：IEEE Press, 1997, 5: 4104-4108.

[17] BARHUMI I, LEUS G, MOONEN M. Optimal training design for MIMO OFDM systems in mobile wireless channels[J].IEEE Transactions on signal processing, 2003, 51(6): 1615-1624.

(编辑：王敏琦)

s：The Program for Changjiang Scholars and Innovative Research Team in University (IRT1299)；The Project of CSTC and Special Fund of Chongqing Key Laboratory (CSTC2013yykfA40010)

Pilot design based on binary particle swarm optimization in the OFDM sparse channel

LIU Yuanhang, LIU Xiaotong, PENG Shuai, WAN Jinjing
(Chongqing Key Lab of Mobile Communications Technology，Chongqing University of Posts and Telecommunications， Chongqing 400065，P.R.China)

The reasonable pilot design can improve the performance of the channel estimation in the OFDM sparse channel. With the objective to minimize the cross correlation of the measurement matrix, this paper proposed a pilot optimization algorithm based on the binary particle swarm optimization algorithm.In addition, the chaos initialization is to ensure that the initial particles are evenly dispersed in the solution space. The particle mutation mechanism is to ensure the rapid convergence of the population. Simulation results show that compared with the random pilot design algorithm, the bitwise pilot design algorithm and the least squares algorithm, the proposed algorithm can effectively save the pilot overhead, improve the spectrum efficiency and provide a better channel estimation performance.

orthogonal frequency division multiplexing (OFDM); compressive sensing; pilot design; binary particle swarm optimization algorithms

2016-04-16

2017-04-13 通讯作者：刘远航 yuanhangl@yeah.net

长江学者和创新团队发展计划(IRT1299);重庆市科委重点实验室专项经费(cstc2013yykfA40010)

10.3979/j.issn.1673-825X.2017.03.008

TN929.5

1673-825X(2017)03-0335-06