流线型箱梁断面涡激力展向相关试验研究

刘志文+龚慧星+陈政清

摘 要：针对闭口流线型主梁结构涡激力展向相关性问题，在均匀流场条件下分别对振动状态和静止状态流线型主梁节段模型进行了不同风攻角的涡激力展向相关性试验研究，分别分析了流线型主梁断面涡激振动响应、涡激力展向相关性及主梁表面压力等.结果表明：振动状态主梁断面涡激力展向相关系数与振幅、锁定区风速等相关，锁定区上升段主梁断面涡激力展向相关系数大于锁定区最大振幅处主梁断面涡激力展向相关系数，扭转涡振锁定区升力矩展向相关系数大于竖向涡振锁定区竖向涡激力展向相关系数；振动状态主梁断面测点压力系数展向相关系数与振幅相关，振幅越大则相关系数越大.

关键词：桥梁；流线型箱梁断面；涡激振动；展向相关性；风洞试验

中图分类号：U441.3 文献标志码：A

文章编号：1674-2974（2017）05-0080-08

Abstract：Aiming at spanwise correlation of vortex-induced forces （VIFs） of the main deck of bridges， wind tunnel experimens of an oscillating and stationary streamlined box girder were conducted under different wind attack angles in the smooth flow. The VIV responses， spanwise correlation of vortex-excited forces， and surface pressures of the streamlined box girder were investigated. The research results showed that the spanwise correlation coefficients of the vortex-excited forces of the streamlined box girder were related to the amplitudes and wind speeds in the lock-in region. The spanwise correlation coefficients of the vortex-excited forces of the main deck at ascending stage of the lock-in region were larger than that of the main deck at the maximum amplitude of the lock-in region. The spanwise correlation coefficients of the pitch moments of the main deck in torsional VIV were larger than that of the lift forces of the main deck in vertical VIV. Meanwhile， the spanwise correlation coefficients of the pressures on measure points of the main deck were related to the amplitudes of the oscillating main deck， and the spanwise correlation coefficients increased with the increase of the amplitudes.

Key words：bridges； streamlined box girder； vortex-induced vibrations（VIV）； spanwise correlation； wind tunnel tests

大跨桥梁结构一般具有频率低和阻尼比小等特性，在风作用下易发生风致振动现象，从而引起桥梁结构疲劳，并影响行车舒适性[1-2]，工程实践中已有多座大桥发生了涡激振动.如英国Kessock桥、第二塞文桥、巴西Rio-Niteroi桥、日本东京湾大桥、丹麦大海带东桥主桥、俄罗斯伏尔加河大桥以及我国西堠门大桥等都发生过程度不同的涡激振动现象，工程实践中一般通过采取气动措施或安装调谐质量阻尼器（TMD）等来控制[3].桥梁结构涡激振动属于典型的非线性振动，具有自激、限幅的特点，同时又受振型、风场以及主梁断面周边流场等因素影响，其振動机理十分复杂[4].

桥梁主梁结构涡激振动具有三维特性，即主梁涡激力沿展向并不完全同步.国内外学者分别针对典型断面和桥梁主梁断面开展了气动力展向相关性研究.Vickery分别进行了均匀流和紊流中静止方柱升力和阻力展向相关性研究，结果表明均匀流场和紊流场条件下静止方柱的升力展向相关长度分别为5.6D和3.3D（D为方柱截面边长）[5].Wilkinson针对方柱振动响应对柱体表面脉动压力展向相关性影响进行了研究，结果表明柱体表面压力展向相关性与结构振动幅值有关[6].Ehsan等针对宽高比为4的H形断面气动力展向相关性进行了研究，结果表明主梁气动力展向相关性还与结构振动自由度有关[7].Haan等对宽高比为6.67的矩形柱体进行气动力展向相关性试验研究，得到该矩形柱体的升力及扭矩的展向相关性与紊流度的关系[8].Nagao等对不同形状平板表面压力进行了试验测试，并对其气动力相关性进行研究，结果表明分离再附区附近压力对气动力展向相关性起着至关重要的作用[9].Matsumoto等分别在均匀流场、紊流场以及正弦脉动风条件下针对矩形断面和带风嘴矩形断面表面压力展向相关性进行了试验研究，研究发现断面分离点之前脉动压力对断面抖振力具有重要影响[10].Ricciardelli针对宽高比为5的矩形断面主梁研究了不同振动形态对气动力展向相关性影响，结果表明结构振动形态对气动力展向相关性有较大影响[11].刘志文等针对宽高比为5的矩形断面柱体涡激力展向相关性进行了试验研究，结果表明涡振锁定区内涡激力展向相关系数大于锁定区外涡激力展向相关系数[12].刘小兵等对宽高比为5∶1的静止矩形断面进行节段模型测压风洞试验，研究了气动力展向相关性随展向间距与来流风攻角的变化规律[13].鲜荣等考虑振型影响采用拉条模型试验研究了钝体箱型断面涡振激力展向相关性[14].Li Hui等对西侯门大桥涡激振动进行现场实测，发现沿桥轴线风压相关性很大，且沿展向并未出现明显衰减[4].张冠华等针对闭口流线型箱梁断面风荷载空间相关性进行了风洞试验研究，研究表明升力、扭矩展向相关性远大于风速及阻力相关性[15].

综上所述，尽管已有许多学者针对不同几何形状断面进行了气动力展向相关性研究，并取得了一定的成果，但对于闭口流线型主梁断面涡激力展向相关性研究相对较少.本文针对闭口流线型箱梁在均匀流场条件下进行了不同风攻角下振动状态和静止状态风洞试验，對其涡激振动响应、涡激力展向相关性及主梁表面压力等进行研究.

1 试验简介

1.1 工程概况

江顺大桥位于广东省江门至顺德之间，跨越西江，主桥为双塔五跨闭口流线型钢箱梁斜拉桥，桥跨布置60+176+700+176+60=1 172 m，桥宽为39.0 m，梁高为3.5 m.中跨采用闭口流线型钢箱梁结构，边跨采用闭口流线型混凝土箱梁，成桥主梁梁底设置检修车轨道和导流板.桥塔塔高为186 m，塔柱截面采用箱形截面.全桥总体布置见图1，主梁标准横断面见图2.

1.2 试验模型

综合考虑，确定主梁节段模型几何缩尺比为1/80，模型长度为L=2.00 m，宽度为B=0.488 m，高度为D=0.044 m，模型长宽比约为L/B=4.1.为了保证模型周围流场为二维状态，在模型两端设置尺寸较大的端板，具体尺寸为600 mm（长）×170 mm（宽）.为了进行模型气动力测试，在主梁节段模型展向不同位置布置了5排测压孔，每排测压截面共布置48个测压点，总计240个测压点，在风嘴、栏杆、检修道等流场变化大区域测压孔布置加密，模型测点布置如图3所示.在每排测压断面附近布置一个64通道的压力扫描模块，将压力扫描阀置于模型内部，粘于模型底板之上，测压管和模型表面测压孔相连，测压管与压力扫描阀模块连接长度约为40 cm，以确保测试结果的准确性.压力扫描阀采样频率为331 Hz，采样时间为20 s.主梁节段模型试验参数见表1.

根据主梁节段模型几何缩尺比和频率等确定主梁节段模型风洞试验风速比为λV=1∶4.94，试验风速为0～10 m/s，非涡振锁定区试验风速步长为ΔV1=0.30 m/s，涡振锁定区试验风速步长为ΔV2=0.10 m/s，试验雷诺数为Re=0～30×104（以模型梁高为参考）.主梁节段模型风洞试验在湖南大学风工程试验中心HD-2边界层风洞中进行，该试验段截面尺寸长17 m，宽3 m，高2.5 m，试验风速范围为0～58 m/s，均匀流场紊流度小于0.5%.试验风速采用澳大利亚TFI公司眼镜蛇风速仪测试，模型振动响应采用激光位移计进行测试.由江顺大桥主梁节段模型抗风性能试验结果可知[16]，该桥主梁在-3°，-5°风攻角下均未观测到涡振现象，故本试验仅针对风攻角为0°，+3°和+5°进行主梁节段模型涡激力展向相关性试验研究，试验模型如图4所示.具体试验工况见表2.

2 试验结果

2.1 主梁涡振响应试验结果

图5所示为主梁节段模型涡激振动响应随折算风速变化曲线.由图5可知，0°风攻角下在试验风速范围内主梁断面未发生明显的竖向涡激共振现象，仅发生了扭转涡激共振，锁定区折算风速为Vr=U/ftB=15.0～20.0，对应的最大扭转响应根方差为0.35°.+3°风攻角下在试验风速范围内，主梁断面出现了两个竖向涡振锁定区，锁定区折算风速分别为Vr=V/fbB=9.0～14.0，20.0～29.0，对应最大无量纲振幅分别为y/D=0.055和0.080；在试验风速范围内出现了两个扭转涡振锁定区，对应锁定区折算风速分别为Vr=U/ftB=8.0～10.0，13.5～18.5，相应最大扭转位移响应根方差分别为0.1°和0.7°.+5°风攻角下在试验风速范围内主梁断面竖向、扭转涡振锁定区与+3°攻角下相应涡振锁定区相近，竖弯及扭转第一锁定区振幅与+3°攻角下相应涡振最大振幅接近，竖弯第二锁定区最大无量纲振幅为y/D=0.135，比+3°风攻角下涡振最大振幅偏大约68%；扭转第二锁定区最大扭转位移根方差与+3°攻角下第二锁定区最大扭转位移根方差接近.

2.2 涡激力展向相关性系数定义

相关系数是反映变量之间相互关系程度的系数，其取值范围为[-1，1].X与Y变量之间的相关系数RXY可由式（1）表达：

式中：X，Y变量换为不同断面间的气动参数变量.根据已有研究成果可知，均匀流场中静止主梁气动力展向相关性系数可表示为式（2）形式，即

式中：ci为与气动力系数Ci相对应的指数衰减系数.静止主梁气动力系数Ci的展向相关性大小也可以用相关长度Li来表示，即

对于振动主梁断面，其气动力是由外部激励力和与振动相关的自激力组成.为了考虑气动力中与主梁运动相关的自激力影响，Ricciardelli提出了如式（4）公式[11]：

式中：di为该指数衰减函数的水平渐近线，即为气动参数中完全相关的部分；ci，di可通过对试验数据进行最小二乘拟合得到.

2.3 振动状态涡激力展向相关性

2.3.1 竖向振动

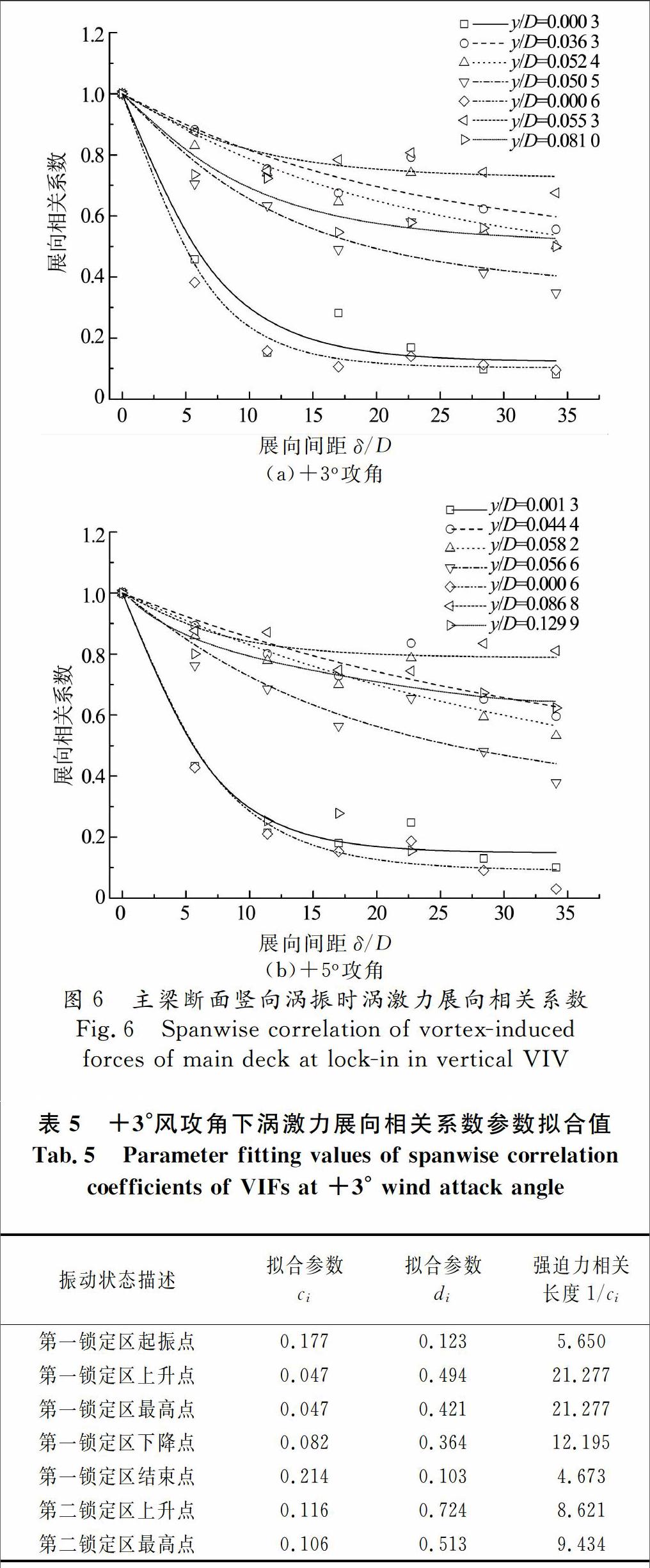
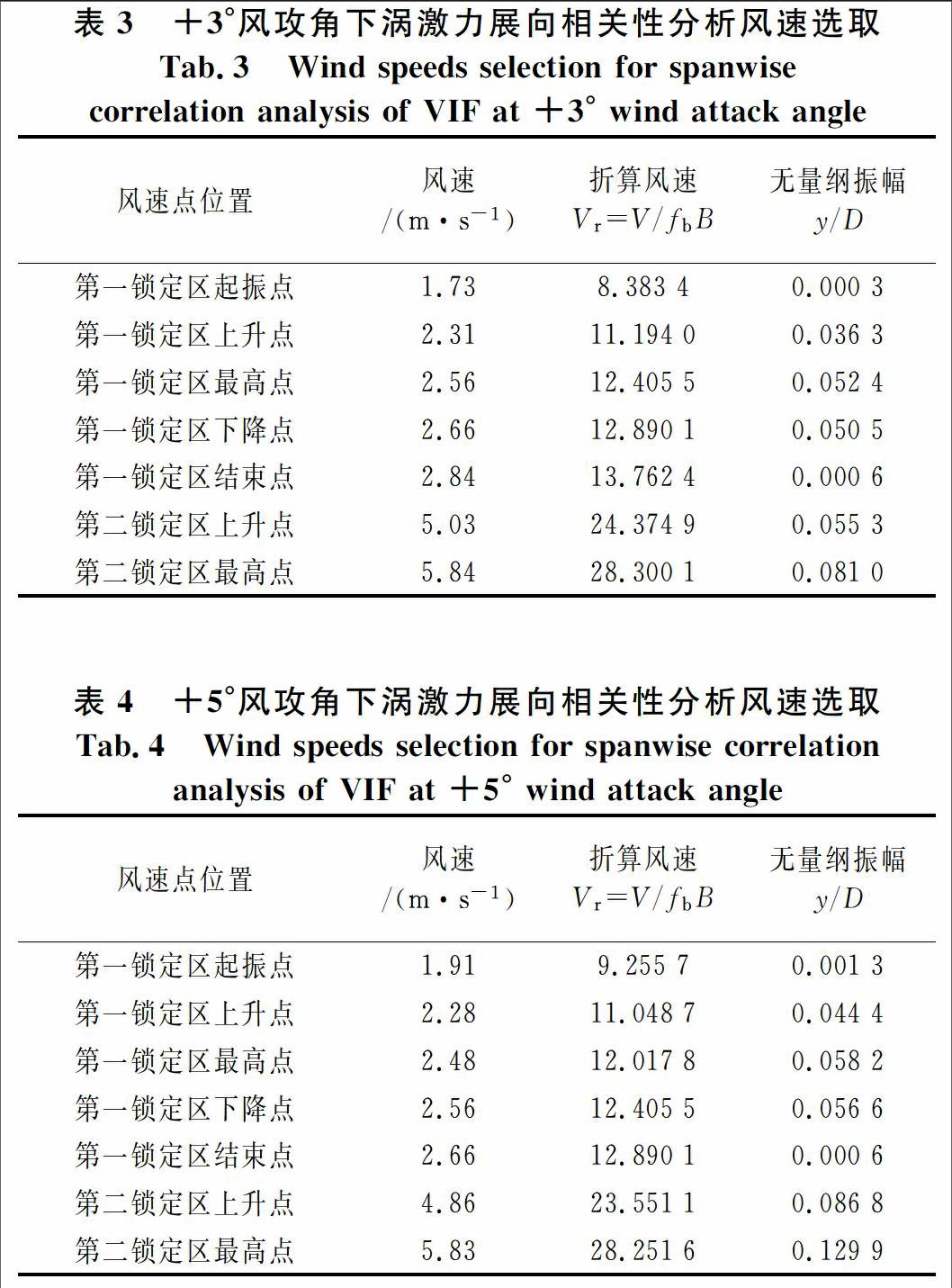
表3，表4分别给出了涡振时气动力展向相关性分析在竖向涡振区间所选的代表性风速.图6（a），（b）所示分别为+3°，+5°风攻角下不同风速对应的升力系数展向相关系数随展向间距变化曲线.值得注意的是，图6（b）中部分试验数据（y/D=0.129 9）与拟合曲线之间有较大的差别，可能与试验数据的采集有关；在进行数据拟合时将离散较大的数据剔除后对应的拟合决定系数为0.988.从图6中可以看出，闭口流线型主梁断面涡激力展向相关系数随展向间距增加而衰减；锁定区起始点和结束点升力系数展向相关系数随展向间距衰减较快，且趋于0；第一锁定区上升段对应涡激力展向相关系数略大于第一锁定区最大振幅对应涡激力展向相关系数，明显大于下降段涡激力展向相关系数.第二锁定区上升段对应涡激力展向相关系数最大，且明显大于第二锁定区上升段对应涡激力展向相关系数；第二锁定区最大振幅对应涡激力展向相关系数与第一锁定区最大振幅对应涡激力展向相关系数接近.+3°，+5°风攻角下主梁断面涡激力展向相关系数随锁定区不同振幅变化趋势一致，+5°风攻角下第2锁定区上升段对应涡激力展向相关系数比+3°风攻角下第2锁定区上升段对应涡激力展向相关系数略大.

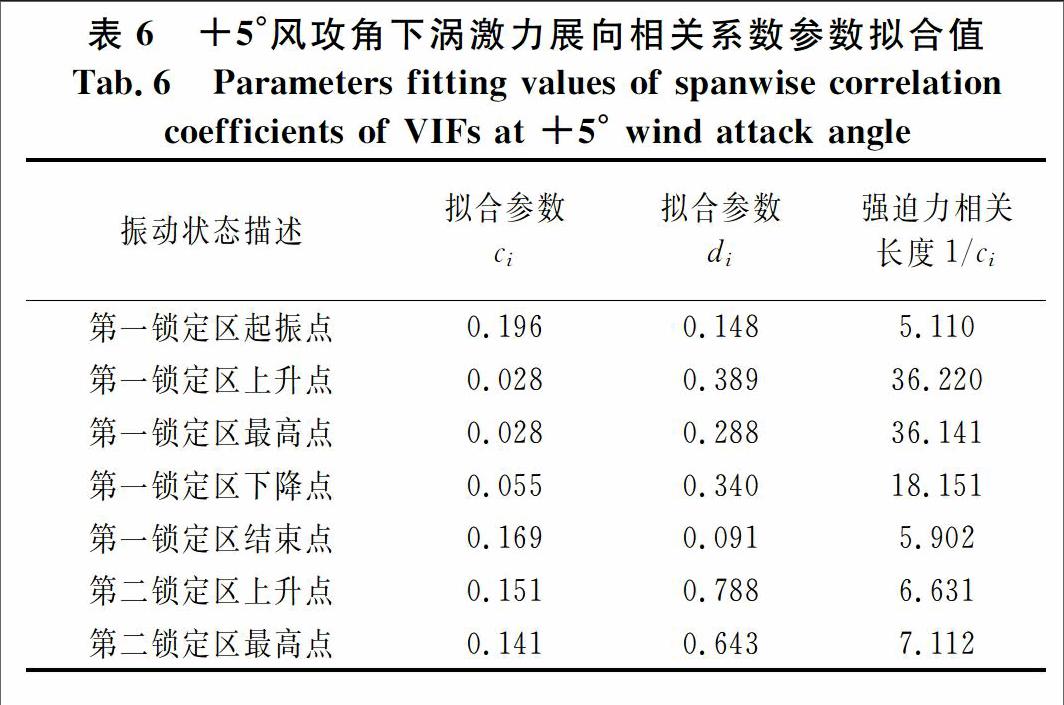
表5，表6分别给出了+3°，+5°风攻角下主梁断面涡振锁定区不同风速对应的涡激力展向相关系数参数拟合值.表中参数ci为与气动力系数Ci所相对应的指数衰减系数；di为该指数衰减函数水平渐近线，即为气动参数中完全相关部分，反映涡激力中自激力部分；展向相关长度1/ci反映了涡激力中强迫力部分.

由表5，表6可知，起振点和结束点di，1/ci值最小，故相对于其它曲线展向相关性较小；上升点di，1/ci值较大，受自激力和强迫力影响最大，故其展向相关性最大.第二锁定区间无论是上升点还是最高点，di值均大于第一锁定区间，但1/ci值小于第一锁定区间，表明第二锁定区间受涡激力主要成份为自激力，而强迫力成份则相对较小，故其展向相关性收敛速度更快且最终展向相关性收敛结果偏大.+5°风攻角下竖弯涡振锁定区内涡激力展向相关系数相应拟合参数变化规律与+3°接近，由于+5°风攻角下第二锁定区振幅较大，故对应di值比+3°风攻角对应di值大，即+5°风攻角下第二锁定区涡激力中自激力占主导，即随着风攻角增大涡振锁定区上升段、振幅最大值对应自激力部分对涡激力展向相关性的影响增大.

2.3.2 扭转振动

图7所示为0°，+3°及+5°风攻角下扭转涡振锁定区第二锁定区上升段、振幅最大值对应的扭转力矩展向相关系数随展向间距的变化曲线.

从图7中可以看出，扭转力矩展向相关系数随展向间距增大整体呈减小趋势，与竖向涡激力展向相关系数相比变化较为缓慢；流线型箱梁断面涡振锁定区升力矩展向相关系数大于竖向涡振锁定区竖向涡激力展向相关系数.

2.4 静止状态升力展向相关性

为了进一步研究锁定区风速、振幅等对升力展向相关性的影响，首先针对+5°风攻角下静止状态主梁断面升力系数展向相关性进行试验，试验风速选取如表4所示；然后分别针对-5°，-3°，0°，+3°及+5°风攻角在5 m/s和10 m/s两个风速下进行静止状态主梁断面升力系数展向相关性试验.考虑到静止状态主梁断面升力系数主要由来流风速引起的强迫力决定，故采用式（2）对主梁断面升力系数展向相关系数实测值进行拟合.图8（a）所示为+5°风攻角下静止状态主梁断面升力系数展向相关系数随展向间距变化曲线.图8（b）所示为不同风攻角不同风速下静止状态主梁断面升力系数展向相关系数随展向间距变化曲线.

由图8（a）可知，+5°风攻角下静止状态主梁断面在各风速下升力系数展向相关系數随展向间距的增加而呈指数衰减，并趋于0；不同风速对应主梁断面升力系数展向相关系数随展向间距变化曲线较为接近.由图8（b）可知，不同风攻角下静止状态主梁断面在各风速下升力系数随展向间距增加呈指数衰减，并趋于0；相对而言攻角绝对值较大时对应升力系数展向相关系数也越大，其主要原因是流线型断面攻角绝对值较大时对应的流动分离强烈，导致升力展向相关性增强.需要说明的是，+3°风攻角在5 m/s风速时升力系数展向相关性明显偏大，其主要原因是该试验风速恰好位于锁定区间上升段，由于试验时模型固定不紧而导致的.

2.5 流线型主梁断面压力分布

从表面压力分布角度对闭口流线型主梁断面涡激力展向相关性进行分析.图9所示为+5°风攻角第二锁定区最大振幅对应风速（5.83 m/s）作用下，振动状态和静止状态主梁断面不同测试断面压力均值及脉动根方差分布图，图中仅标出了测试断面3对应压力数值.由图9可知，主梁断面不同测压断面压力系数均值与均方差分布总体较为接近；振动状态与静止状态主梁表面压力系数均值接近，且在检修车轨道下游侧梁底均出现了明显的局部负压区；振动状态主梁断面压力系数根方差明显大于静止状态主梁断面压力系数根方差.

图10所示为+5°风攻角下流线型主梁断面表面26#，33#测点压力系数展向相关系数随展向间距变化曲线.

由图10可知，振动状态测点压力系数展向相关系数大于静止状态测点压力系数展向相关系数；振动状态测点压力展向相关系数与振幅相关，振幅越大则展向相关系数越大；静止状态测点压力系数展向相关系数总体比振动状态小，随展向间距增大而趋近于0.振动状态26#测点（位于下游斜腹板靠近风嘴处）压力系数展向相关系数大于33#测点（位于底板靠近斜腹板处）压力系数展向相关系数.

3 结 论

在均匀流场条件下进行了不同振动状态、不同风攻角流线型主梁断面涡激力展向相关性试验研究，得到如下主要结论：

1）振动状态主梁断面涡激力展向相关系数与振幅、锁定区风速等相关，锁定区上升段对应涡激力展向相关系数大于锁定区最大振幅对应涡激力展向相关系数；扭转涡振锁定区升力矩展向相关系数大于竖向涡振锁定区竖向涡激力展向相关系数.

2）静止状态不同风攻角不同风速下主梁断面升力系数随展向间距增加呈指数衰减，并趋于0，攻角绝对值较大时对应升力系数展向相关系数也越大.

3）振动状态主梁断面测点压力系数展向相关系数与振幅相关，振幅越大则相关系数越大.

参考文献

[1] 项海帆，葛耀君，朱乐东，等. 现代桥梁抗风理论与实践[M]. 北京：人民交通出版社，2005：1-6.

XIANG Haifan， GE Yaojun， ZHU Ledong， et al. Modern theory and practice on bridge wind resistance[M]. Beijing： China Communication Press， 2005：1-6.（In Chinese）

[2] 陈政清. 工程结构的风致振动、稳定与控制[M]. 北京：科学出版社，2013：371-419.

CHEN Zhengqing. Wind induced vibration， stability and control of engineering structures[M]. Beijing： China Science Publishing & Media Ltd， 2013：371-419.（In Chinese）

[3] 陈政清， 黄智文，王建辉，等. 桥梁用TMD的基本要求与电涡流TMD[J]. 湖南大学学报：自然科学版，2013，40（8）：6-10.

CHEN Zhengqing， HUANG Zhiwen， WANG Jianhui， et al. Basic quirements of tuned mass damper for bridges and the eddy current TMD[J]. Journal of Hunan University：Natural Sciences， 2013， 40（8）： 6-10.（In Chinese）

[4] LI Hui， LAIMA Shujin， OU Jinping， et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J]. Engineering Structures， 2011， 33： 1894-1907.

[5] VICKERY B J. Fluctuating lift and drag on a long cylinder of square cross section in a smooth and in a turbulent stream[J]. Journal of Fluid Mechanics， 1966， 25（3）： 481-494.

[6] WILKINSON R H. Fluctuating pressures on an oscillating square prism. Part II： spanwise correlation and loading[J]. Aeronautical Quarterly， 1981， 32（2）： 111-125.

[7] EHSAN F， SCANLAN R H， BOSCH H R. Modeling spanwise correlation effects in the vortex-induced response of flexible bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1990， 36（2）： 1105-1114.

[8] HAAN JR F L， KAREEM A， SZEWCZYK A A. Experimental measurements of spanwise correlation of self-excited forces on a rectangular cross section[C]// NIEMANN H J. Proc 4th International Colloquium on Bluff Body Aerodynamics and its Applications. Bochum： Ruhr-University， 2000.

[9] NAGAO F， UTSUNOMIYA H， NODA M，et al. Basic study on spatial correlations of fluctuating lifts acting on plates[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2003， 91： 1349-1361.

[10]MATSUMOTO M， HIROMICHI S， KENJI A，et al. Spanwise coherence characteristics of surface pressure field on 2-D bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2003， 91（1/2）： 155-163.

[11]RICCIARDELLI F. Effects of the vibration regime on the spanwise correlation of the aerodynamic forces on a 5∶1 rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2009， 98（4/5）： 215-225.

[12]劉志文，黄来科，陈政清. 宽高比为5的矩形断面柱体涡激力展向相关性试验研究[C]// 中国土木工程学会桥梁及结构工程分会风工程委员会，第十六届全国结构风工程学术会议暨第二届全国风工程研究生论坛论文集.成都：西南交通大学出版社，2013：101-102.

LIU Zhiwen， HUANG Laike，CHEN Zhengqing. Experimental study on spanwise correlation of vortex-induced forces of rectangular cylinder with aspect ratio of 5[C]// Wind Engineering Committee of Bridge and Structural Engineering Branch of China Civil Engineering Society， The Conference of the 16th National Conference on Structural Wind Engineering and the 2rd National Forum on Wind Engineering for Graduate Students. Chengdu： Southwest Jiaotong University Press， 2013：101-102.（In Chinese）

[13]刘小兵，张海东，王彦彪. 宽高比为5的矩形断面梁气动力展向相关性研究[J].工程力学，2015，32（Suppl）： 50-54.

LIU Xiaobing， ZHANG Haidong， WANG Yanbiao. Study on spanwise correlation of aerodynamic force of rectangular cylinder with aspect ratio of 5[J]. Engineering Mechanics， 2015， 32（Suppl）： 50-54.（In Chinese）

[14]鮮荣.大跨度桥梁沿跨向主梁涡激振动研究[D].成都：西南交通大学土木工程学院，2008：78-96.

XIAN Rong. Investigation of long-span bridge girder spanwise vortex-induced vibration[D]. Chengdu：College of Civil Engineering， Southwest Jiaotong University， 2008：78-96.（In Chinese）

[15]张冠华，赵林，葛耀君. 流线型闭口箱梁大断面风荷载空间相关性试验研究[J]. 振动与冲击，2012，31（2）：76-80.

ZHANG Guanhua， ZHAO Lin， GE Yaojun. Spatial correlation of wind loads for cross-section of a streamlined closed box girder[J]. Journal of Vibration and Shock， 2012， 31（2）： 76-80.（In Chinese）

[16]刘志文，洪涵，梁立农，等. 广东江顺大桥抗风性能试验研究[J]. 湖南大学学报：自然科学版，2015，42（3）： 112-119.

LIU Zhiwen， HONG Han， LIANG Linong，et al. Experimental investigation of the wind-resistant performance of Jiangshun bridge in Guangdong[J]. Journal of Hunan University：Natural Sciences， 2015， 42（3）： 112-119.（In Chinese）