中国长白山脉松毛虫害的网络建模与分析

冯颖，刘晓，吕双十

（1.辽宁林业职业技术学院，辽宁沈阳110101；2.东北大学，辽宁沈阳110819）

中国长白山脉松毛虫害的网络建模与分析

冯颖1，刘晓2，吕双十1

（1.辽宁林业职业技术学院，辽宁沈阳110101；2.东北大学，辽宁沈阳110819）

该文基于生态位法则和竞争排除原理提出了林木虫害的时空影响域网络模型，利用该模型构建了2009-2013年的长白山脉松毛虫害关系网络拓扑结构，并对该网络结构的无标度性、节点重要性、平均路径长度等结构特征量进行了分析，结果表明，松毛虫虫害的发生因周围发生地区的松毛虫扩散直接导致的可能性不大，松毛虫网络节点连通性不好，网络比较疏松。

松毛虫；网络科学；时空影响域

随着以互联网为代表的网络信息技术的迅猛发展，人类社会已经迈入了复杂的网络时代[1]。网络科学自诞生之日到现在的十几年间，不仅理论研究取得了突破性进展，发现了诸多令人瞩目的崭新成果，而且更成为了探索新的交叉科学的一种强有力的思想方法[2]。本文首次将网络科学的分析方法运用到林木虫害研究领域，力求通过虫害网络的数据分析找出虫害发生发展的规律，为林木虫害的预测预报提供有价值的参考信息。

1 网络结构特征量定义

定义1：度，节点i的度是指与其连接的其它节点的数目，记做ki。网络的平均节点度即为kˉ，则

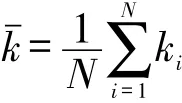
式中：N为网络中节点的数目。

定义2：出度，对于有向网络N1，以顶点V1为起点的边的个数，称为顶点V1的出度[3]。

定义3：入度，对于有向网络N2，以顶点V2为终点的边的个数，称为顶点的入度。

网络中边的入度和出度分布满足某些特定的规律。实证研究表明，有向网络中存在入度和出度的双向幂律分布。

有向网络中的边都存在入度与出度两个度值，有向网络中的边是具有方向性的。

与有向网络相对的是无向网络，在无向网络中连接没有方向，因此也就没有入度和出度的区别，而只有度的概念。

定义4：度分布，是指图G＝(V,E)中所有节点的度的分布情况，通常用分布函数P(k)来描述。P(k)是对任意节点i，恰好使得ki=k的概率。

定义5：聚类系数，是衡量网络中节点的邻居之间紧密程度的参量[4]。节点i的聚类系数，为该节点与邻居节点之间实际存在的连接数目Ei与可能存在的最大连接数目之比，记为Ci，即

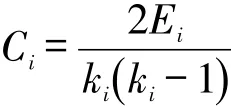
整个网络的聚类系数C，则为网络中所有节点聚类系数的平均值：

定义6：网络结构熵，

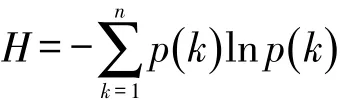
其中：p(k)为网络拓扑中度值为k的概率；n是网络拓扑节点总数。在复杂网络中，网络的无序程度用熵值来描述。

定义7：网络K-核，在网络图中，核是指反复去掉度数小于和等于K的节点后所剩余的子图[5]。核数[6]表示包含该节点的最深的核，即节点存在于K-核中，但是在(K+1)-核中被移除，则节点的核数为K，节点核数的最大值即为网络的最大核数。可以通过K-核解析将网络从外层到内层一层层地解析直到网络的最内层，从而揭示网络的层次结构性质[7-9]。如图1所示，最外层为0核，最内层则为网络的最大核。

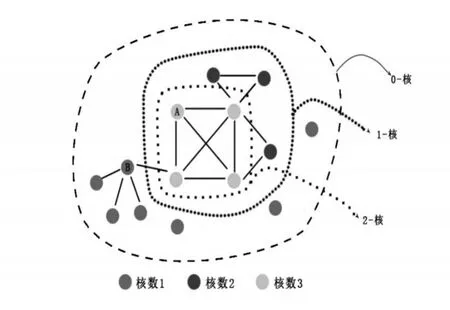
图1 k-核解析图

2 时空影响域网络模型

何璇等(2014)针对地震事件在时间和空间表现出的相关性，首次提出了一种基于时空影响域的网络模型，根据震级的大小来确定某次地震事件在时间和空间上产生的影响范围。每一次地震在地表上会形成一个空间影响区域S，S是以自身为圆心的圆形区域，而地震所形成的时间影响域T的大小取决于地震波衰减所经历的时间。由此，每次地震均可产生一个时空影响域U(S,T)，在该时空影响域U内，如果再次发生地震则被视为是由本次地震直接影响而产生的，而在该影响域之外发生的地震均被视为与本次地震无直接关系[10]。

一次地震发生之后，在某一时间和空间的范围内会产生一定影响，而震级越大，其产生的影响范围也就越大，因此确定了震级与影响半径之间的关系式为：

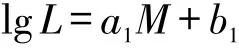
式中：M为震级；L为对应震级地震产生的影响半径；a1和b1为常量[10]。

由于林木虫害的发生与地震事件的发生有很多相似处，比如说地震事件有突发性，林木虫害也同样具有爆发性；另外地震事件有不同的震级，林木虫害也根据其危害程度分为轻度、中度、重度级别，而且危害级别越大，产生的影响范围也就越大，地震与虫害一样都波及一定的影响区域；地震会带来大小不等的多次余震，虫害也会带来轻重不等的次生灾害等。正是因为林木虫害事件与地震有如此多的相似之处，那么尝试用时空影响域的方法来探索林木虫害关系网络的构建。

定义8：时空影响域，某地发生虫害之后，该点对周围空间的影响范围及其持续影响的时间窗口，定义为时空影响域。其中，空间影响半径，指虫害发生后，相同生态位的昆虫之间由于竞争产生种群取食压力，当地昆虫种群会向周围的空间范围扩散，对周围林地造成影响的范围；对于时间窗口，是指当虫害在某一时间发生后，害虫种群在当地及其空间影响范围内造成影响的持续时间。

需要明确的是，虫害发生愈严重，生态压力愈大，其需要向周围空间扩散的能力愈强，即在空间上产生影响范围就越大；另外，时间窗口长度为昆虫危害属性，不受虫害发生严重程度影响（对于同类害虫，在时间上造成持续影响的时间窗口长度相等）。下面给出林木虫害灾害等级指数（即虫害发生严重程度）与空间影响半径的关系模型：

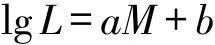
式中：L为虫害影响区域半径；M为林木虫害危害等级指数；a与b为常量，且a，b的值会因地理位置不同及昆虫种类不同而异。

该模型中对于林木虫害灾害等级指数M的计算，以国家林业局颁布的《林木病虫害预测预报管理办法》中对林木病虫害危害程度等级分级标准为依据，将虫害对森林造成的损失程度划分为轻、中、重3级（分别赋权值1，2，3）。根据调查统计结果，确定林木虫害危害程度及面积，计算林木虫害危害等级指数M[11]。

定义9：昆虫网络为有向图G=(V,E)，其中V为图G的节点集||V=n，每个节点代表森林病虫防治调查中实际发生的虫害；E指网络中有向边构成的集合||E=e，对于任意两个节点i∈V和j∈V，设Ri(Ti，Si)为节点i的时空影响域，Rj(Tj，Sj)为节点j的时空影响域，如果两个影响间处于包含或交叉关系，则存在一条边(i，j)使i指向j，且将处在相同生态位上的同类昆虫对空间影响范围及时间窗口内产生的影响作用视作相同。

每次虫害的发生在空间及时间上都会造成一定范围的影响，发生一次虫害后在该区域及附近会形成一个以自身为圆心的圆形影响区域S；而虫害对周围区域产生持续影响的时间窗口大小为T。由此，每次害虫发生均会产生一个时空影响区域R（T, S），在该影响区域内再次发生的虫害均视为由本次虫害直接影响所导致的，而在该影响区域之外发生的虫害则视为与本次虫害发生无直接关系。在本文对昆虫网络的探索中，以虫害发生地经纬坐标定为节点，相同坐标节点，且在相同时间窗口内发生的虫害视为同一节点。如图2所示，在tA时刻虫害A发生并形成影响域RA(TA,SA)，而在tD时刻虫害D发生，由于tD＞tA+TA（D处在虫害A的影响时间窗口之外），即A地发生的虫害在D发生之前，种群就已经消失，害虫不再向周围迁移，不对外界造成影响，所以无论D点是否在A点的空间影响半径SA内，均被认作虫害A对虫害D无直接影响，即不构成连边。另一种情况，在tB时刻B点发生虫害，之后在tC时刻C点也发生虫害，由于C点在B的时空影响域内，即C既在B的空间影响半径内又在其产生的影响时间窗口中，因此视B对C有直接影响，即存在一条由B指向C的有向边。

以图3为例，依据时空影响域模型构建昆虫网络，根据计算得到每次虫害发生后形成的空间影响半径如图3（a）中白色圆形区域所示，由于虫害发生轻重程度不同，形成的白色区域面积亦有差异，其中重叠部分说明地区间虫害存在影响关系；如图3（b）所示，虫害发生时间顺序为从A到I，并假设该类虫害造成影响的时间窗口长度为3个时间单位，如图3（b）中条带覆盖的时间长度所示，即在0时刻发生的虫害所造成的影响只能持续到时刻2。那么根据定义1，示例的网络拓扑如图3（c）所示，0时刻A处发生虫害在时间上形成的影响会持续到时刻2，但其形成的空间影响半径并未覆盖至2时刻发生虫害的B处，因此不存在连边；B、C在相同地点，可看作同一节点，且C发生的时间在B产生的时间影响窗口内，因此产生一条自连边；网络中其他节点的定义及连边关系以此类推。

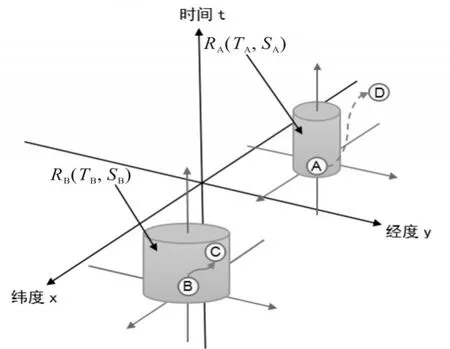
图2 基于时空影响域构建网络示意图

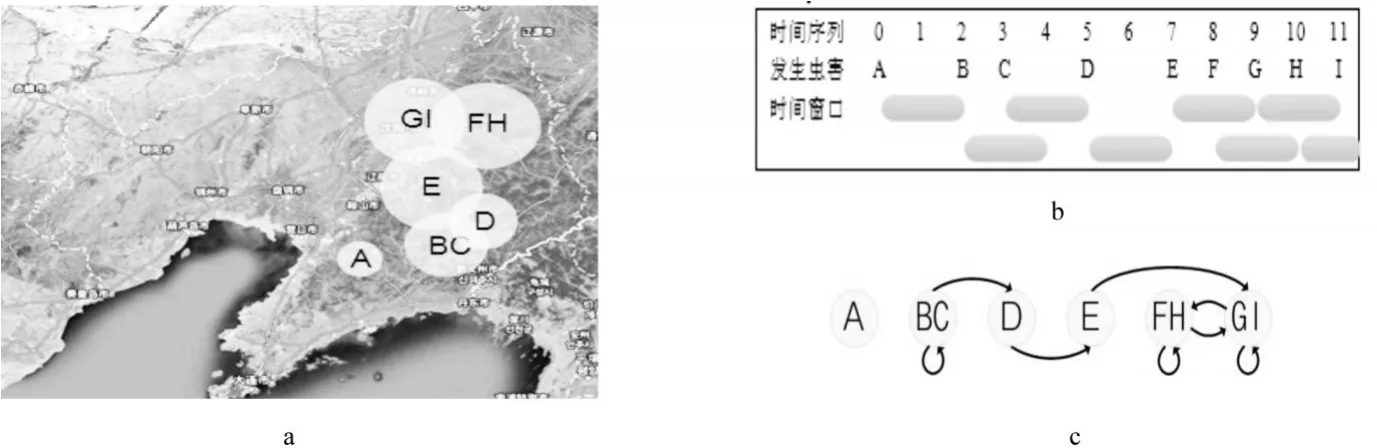
图3 基于时空影响域构建昆虫网络

3 松毛虫类虫害网络构建

3.1 数据选取

本文采自2009-2013年长白山脉林区松毛虫类虫害监测数据。根据林木病虫害历年调查结果，松毛虫类害虫是长白山脉林区对针叶林危害最严重的食叶类害虫。分布在长白山脉林区的松毛虫种类主要有3种，分别为落叶松毛虫Dendrolimus superans、油松毛虫D.tabulaeformis、赤松毛虫D. spectabilis。

由于松毛虫类害虫发生量大，且生活习性与生态位均相类似，故本文以生态位相同的松毛虫类多个种群间的害虫为研究对象，建立长白山脉林区松毛虫类虫害关系网络。

松毛虫类虫害网络是基于时空影响域模型而构建的，在进行网络构建前首先对时间影响窗口及空间影响域半径分别做如下说明：松毛虫发生造成持续影响的时间窗口设为不超过12个月；根据松毛虫的生活习性，最长迁飞距离不超过37 km，故将空间影响域半径L上限设为37 km[12]。

3.2 松毛虫虫害网络

从2013年林木病虫害发生防治统计数据中筛选出了松毛虫类害虫的监测发生面积数据，基于时空影响域网络模型，建立了长白山脉松毛虫属害虫虫害网络。网络中节点数有106个，有向边282条。网络的节点数即这个网络中所有节点的个数，我们将不同月份监测到的松毛虫虫害发生地区作为节点，节点数在一定程度上体现了网络规模的大小。连边是对网络规模的另一种衡量方式，表示节点间连接的总边数，把该网络中的不同节点间存在关联关系的节点间进行连边。该网络为有向网络。网络拓扑如图4所示。图4数据来源为2013年松毛虫类害虫监测发生数据。图中圆点表示节点，即不同月份监测到的松毛虫虫害发生地区；图中连线为边，即两个虫害发生地区产生关联。

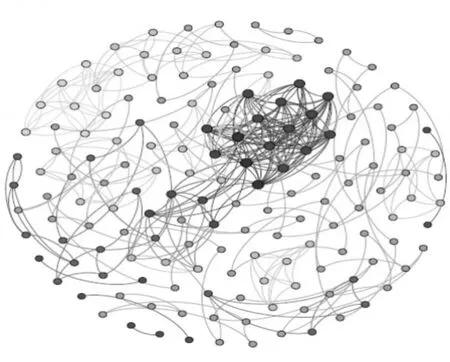
图4 松毛虫虫害关系网络可视化图

4 网络结构分析

4.1 无标度特征

节点度分布是真实网络不同于随机网络的一个最基本的特征。我们把节点度分布服从幂率分布的网络称为无标度网络。许多实际大规模网络，其幂指数在2≤λ≤3区间。在真实网络中，绝大多数节点的度相对很低，但也存在着少量度值相对很高的节点，我们把这种节点度分布服从幂律分布特性称为网络的无标度特性[13]。

通过对长白山脉2013年松毛虫虫害关系网络的度分布分析发现，其不服从幂率分布，也不具有小世界特征，但松毛虫网络结构的出度与入度分布服从幂率分布。如图5所示，图中直线表示以幂律对其度分布概率进行拟合的结果，拟合系数分别为0.875 66、0.899 39。

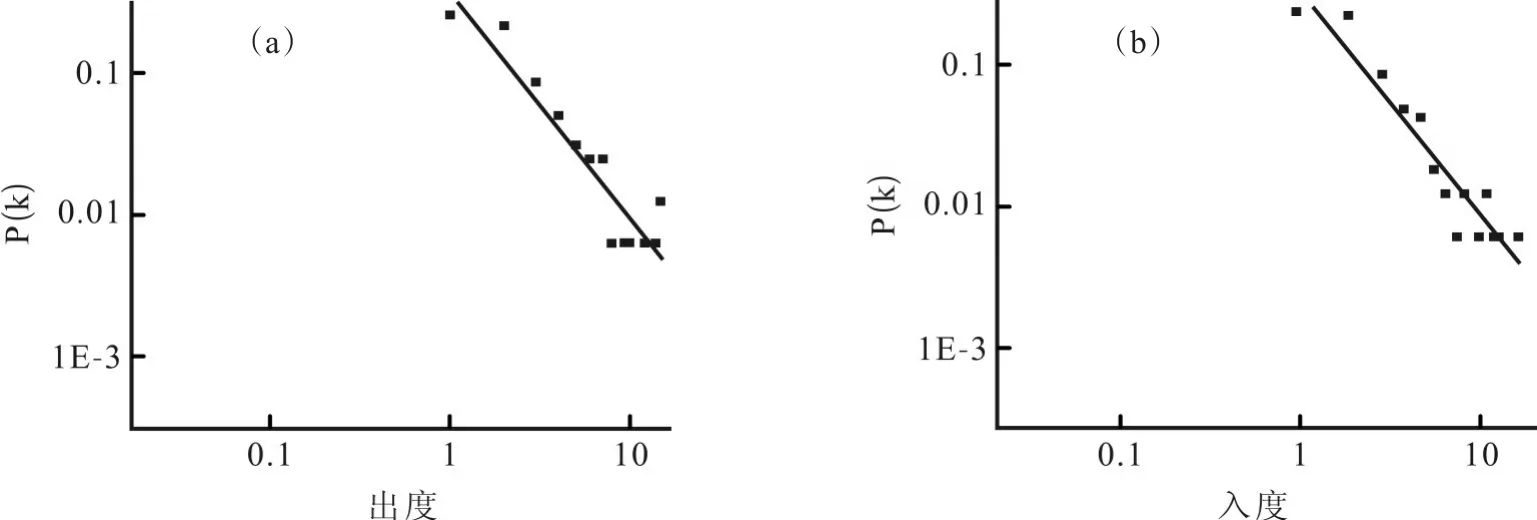
图5 松毛虫网络节入度与出度分布

以上分析说明从长白山脉松毛虫虫害整体情况来看，某一节点地区的松毛虫虫害发生是由另一虫源节点地区虫害扩散而引起的可能性不大。另外发生松毛虫虫害地区彼此间产生的影响很小，只有在地理搭界的节点地区间才有产生影响的可能。

4.2 重要节点分析

松毛虫虫害关系网络节点度值分布如图6所示。由此可见，小度值节点占比较大。

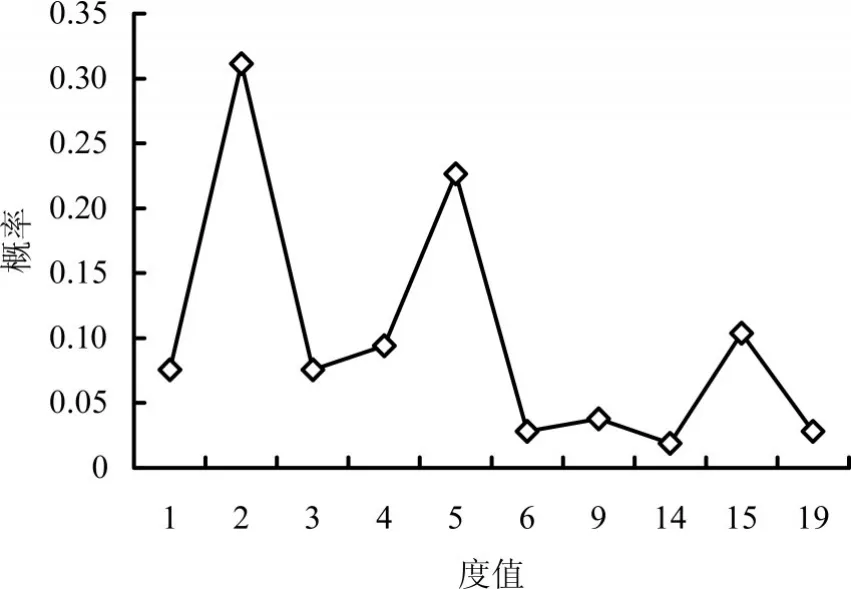
图6 松毛虫虫害关系网络节点度值概率

选取长白山脉林木虫害发生地区中位于大度值前5位的节点地区的松毛虫情况进行分析，这5个地区分别位于金州区、大连市区、甘井子、普兰店市、瓦房店市。其中金州区发生的松毛虫种类为赤松毛虫，大连市发生的松毛虫种类为油松毛虫和落叶松毛虫，甘井子地区发生的为赤松毛虫。

金州区节点地区在松毛虫虫害关系网络中是度值最高的节点，说明它也是松毛虫虫害关系网络中与周围地区影响最广泛的节点。通过对数据的分析可知，金州区松毛虫虫害同大连市区、普兰店市、甘井子区的松毛虫虫害相互之间影响很大，这4个节点地区有松毛虫彼此间相互传播的可能。

金州区、大连市区、甘井子区、普兰店市、瓦房店市都属于辽东半岛地区，辽东半岛在地貌上属于低山丘陵，半岛因伸入海洋，受海洋影响较大，气候温暖湿润，属暖温带季风气候。辽东半岛的年均温8～ 10℃，最热月均温24～25℃，最冷月均温－10～－5℃，无霜期160～215 d，年降水量550～900 mm，所有这些环境因子为松毛虫的生长与发育创造了有利的条件。另外，从地理位置可以看出，这4个地区的松毛虫寄主林区距离较近，在松毛虫扩散理论距离的范围内，所以相互间产生影响的可能性极大。在实际森防工作中，可以对此类重要节点进行重点防治，且可以尝试把防治工作适量偏转到对“重要节点与外部节点的连边”的阻断和干扰上。当然相联系的节点地区要尽力采取“联防联治”的策略，这样会收到更理想的防治效果。

松毛虫发生严重节点地区的度值情况如表1所示。通过分析发现，虽然这些地区发生非常严重，但度值却很小，这说明这些节点地区与其它节点地区连边较少，产生的影响不大。所以这些地区在防治策略上可采取局部单点防治的方法。

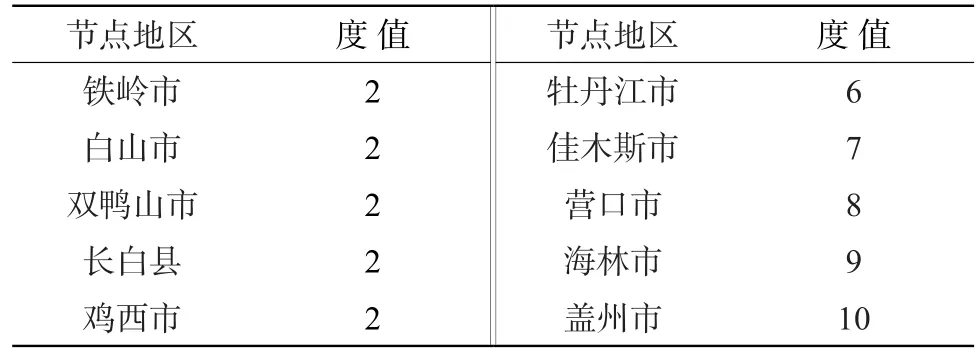
表1 虫害发生严重地区的度值

4.3 平均路径长度

在复杂网络中，网络的平均路径长度L是网络中任意节点之间最短路径的平均值，是衡量网络通讯和传输能力的重要参数，也是衡量网络鲁棒性的重要拓扑特征量。L越短，网络中微小扰动对网络造成致命打击的可能性越小，即网络拓扑鲁棒性越好[14-15]。

松毛虫网络平均路径长度L=1.277，可见松毛虫网络平均路径长度较短，说明该网络的网络鲁棒性高，发生虫害之后，在外界作用下，无论对节点的控制或对连边的阻碍作用，都对网络拓扑无法形成打击甚至影响。

4.4 平均聚集系数

聚集系数用来描述网络中节点的聚集情况，即网络有多紧密。网络的聚集系数越大，其邻居节点之间连边越多，因此局部连通性越强。松毛虫网络平均聚集系数C=0.469，聚集系数不高，说明松毛虫网络节点之间整体连通性不好，害虫发生地会对周围林地造成的影响不广泛。网络中节点与其邻居节点间的相互影响比较疏松，即松毛虫虫害的发生未呈现一定的聚集现象；网络由于拓扑结构比较松散，对外部干扰具有的自愈能力较差。

4.5 网络的平均度

松毛虫网络平均度值为2.242，说明具有相互联系的节点不多，整体网络散点较多。因为松毛虫主要危害针叶树种，而对于针叶树种密集的林区，地理位置彼此间隔距离大，远远超过松毛虫扩散的范围，所以发生松毛虫虫害的相互影响的可能性小。

4.6 网络的结构熵

熵的宏观意义是系统能量分布均匀性的一种量度，如果物体所处状态越稳定，能量分布越均匀，则熵值越大。

长白山脉松毛虫虫害关系网络的结构熵为0.351 9，熵值较小，说明该网络的稳定性较差。

4.7 网络的K-核

通过网络K-核分析，可以找到高核聚集区，即林木虫害高度爆发地区。长白山脉松毛虫网络各节点K-核分布如图7所示。曲线波动较大，处于低核的节点数较多，核值是1的点占30.48%，这说明整个网络大部分节点连接不紧密，松毛虫发生的地区中单散孤立的点较多。

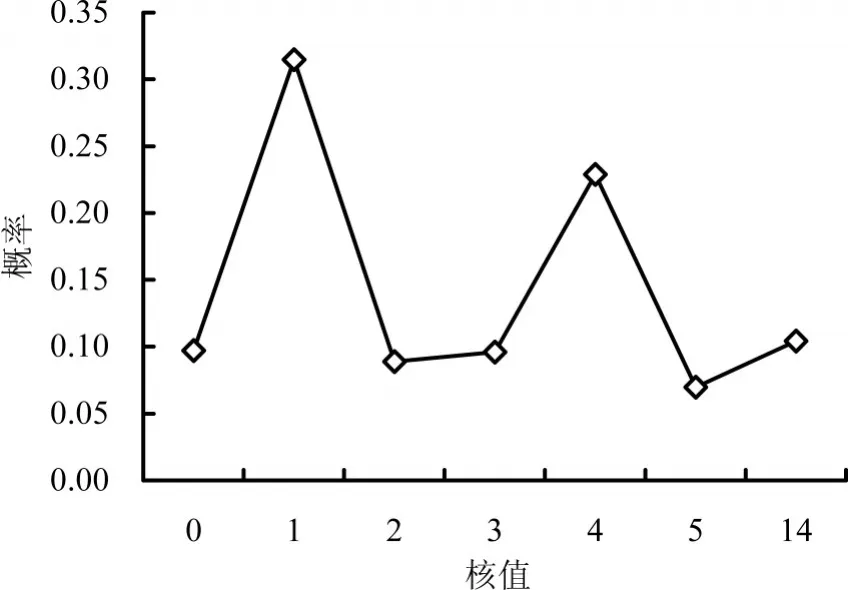
图7 松毛虫虫害关系网络核概率分布

核值最高为14，占比为10%，位于高核的节点地区分别为抚松县、大连市、海林市、依兰县、鲅鱼圈区、敦化市、蛟河市、桦南县、延寿县、通化市、大石桥市、集贤县。从表2可以得出结论，松毛虫虫害关系网络中位于高核区的节点的度值并不都为大度数节数，也就是说是否位于高核地区与节点的度值没有绝对的关系，高度节点也并不都处于高核地区。

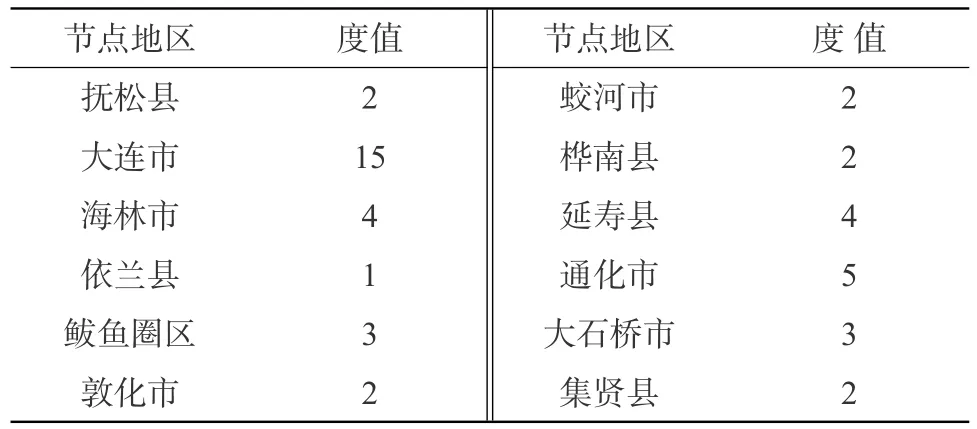
表2 位于高核区节点对应度值

4.8 虫害发生地区数的变化

2009-2013年每年12月份长白山脉不同种类松毛虫虫害发生地区的节点数变化见图8。

图8 2009-2013年松毛虫害发生地区数量变化

从图8可见，2010年节点数比2009年稍有减少后，持续呈上升趋势，这表示松毛虫虫害危害这几年来始终居高不下。

2009-2013年每年新生与消亡节点变化情况如图9所示，以每年12月份为界。2010-2013年3年间每年新生节点数分别为13、11、12，都在10个以上，这说明松毛虫分布区域在急剧扩大。在新生节点地区中，出现发生反复的节点数有3个，分别是林口县、鸡西市和鸡东县。除了这3个反复节点之外，净增加新生节点数共为33个。

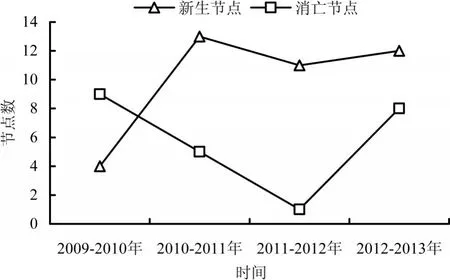
图9 2009-2013年每年新生与消亡节点变化

4.9 节点介数

介数反映了相应的节点或者边在整个网络中的作用和影响力，是一个重要的全局几何量，介数通常分为边介数和节点介数两种。节点介数定义为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例[16]。

通过对长白山脉松毛虫虫害关系网络介数分析，发现存在着大量介数为0的叶子节点，说明独立存在的节点较多。介数大的节点有延寿县、鸡东县和汤原县，介数为30；开原市、汪清县、西丰县节点介数为12。可以得出以下结论：延寿县、鸡东县、汤原县、开原市、汪清县和西丰县这6个节点地区在长白山脉松毛虫虫害关系网络中的地位很重要，起到了一定的桥梁作用。

5 小结

本文基于时间与空间影响域模型，根据松毛虫生活习性确定时间影响范围，并根据林木虫害危害等级指数大小确定空间影响半径的范围。通过对2009-2013年长白山脉林木松毛虫虫害发生数据的统计与分析，建立松毛虫网络，同时，以复杂网络研究手段分析松毛虫网络特征量。得出如下结论：松毛虫虫害的发生因周围发生地区的松毛虫扩散直接导致的可能性不大，松毛虫网络节点连通性不好，网络比较疏松。

本文采用时空影响域网络分析模型对长白山脉松毛虫属虫害关系网络进行分析，结果可知，借鉴地震网络而构建的时空影响域模型运用在虫害网络研究上还存在一定的局限性，因为虫害网络与地震网络特性具有很大不同。在不同的地域，虫害可以同时有多处虫源地区并存，可以多点虫害同时爆发。害虫具有一定的规律性生命周期，虫害的发生不仅受寄主的分布、温湿度等自然环境因子的影响，而且还与人类的活动密不可分。

［1］蒋峰岭.基于加权网络的公交网络换乘模型的优化及其性能的研究［D］.杭州：浙江工业大学，2011.

［2］方锦清，毕桥.统计物理与网络科学面临的若干挑战与思考［J］.复杂系统与复杂性科学，2010，7(4):29-38.

［3］张文波.Internet宏观拓扑结构的生命特征研究［D］.沈阳：东北大学，2006.

［4］弭雪.基于复杂网络的嵌入式互联网统计时间特征关键问题研究［D］.沈阳：东北大学，2014.

［5］李光光，赵海，何璇，等.基于k-核解析的地震活动网络特征分析［J］.地震学报，2015，37(2)：239-248.

［6］Alvarez-Hamelin J I.k-core decomposition:a tool for the visualization of large scale networks［J］.Computer Science，2005，（18）.

［7］郎丰高.互联网宏观拓扑及病毒传播分析［D］.沈阳：东北大学，2011.

［8］付大愚.互联网宏观拓扑结构的分形特征研究［D］.沈阳：东北大学，2011.

［9］Wang H,Hernandez J M,Van M P.Betweenness centrality in a weighted network［J］.Physical Review E-Statistical, Nonlinear,and Soft Matter Physics,2008,77(4):46105.

［10］何璇，赵海.基于时空影响域的地震网络构造方法［J］.东北大学学报（自然科学版）2014，35(10):1395-1399.

［11］陈凤学，赵杰，耿海东.森林病虫害灾害等级研究［J］.中国森林病虫，2004，23(3):4-7.

［12］车锡冰，夏乃斌，宋长义，等.油松毛虫成虫迁飞特性的研究［J］.北京林业大学学报，1996，18(3):61-65.

［13］马宇，葛伟，田敏爵，等.我国森林病虫害防治现状与对策［J］.陕西林业科技，2011，（1）:51-53.

［14］Réka Albert,Albert-László Barabási.Statistical mechanics of complex networks［J］.Review of Moden Physics,2002, 74(1):47-97.

［15］J Ash,D Newth.Optimizing complex networks for resilience against cascading failure［J］.Physica A: StatisticalMechanicsandits Applications，2007, (308):673-683.

［16］刘涛，陈忠，陈晓荣.复杂网络理论及其应用研究概述［J］.系统工程，2005，(6):1-7.

(责任编辑：苑辉)

Network modeling and analysis of damage caused by pine moth in Changbai Mountain,China

FENG Ying,LIU Xiao,LV Shuangshi
（1.LiaoningForestryVocation-TechnicalCollege,Shenyang110101,China;2.NortheasternUniversity,Shenyang110819，China）

Based on the niches rule and the competitive exclusion principle,a model of space-time influence domain about the pest was proposed.According to this model the pine moth relationship networks of Changbai Mountains were extracted from 2009 to 2013，and then the scale-free of network，important nodes and average path length were studied. The statistical results showed that the damage was less likely caused by pine moth which diffused from neighbor area, the network node connectivity of pine moth was bad and network was loose.

pine moth;network science;space-time influence domain

763.3

A

1001-1714（2017）03-0015-07121

2016-10-30

冯颖（1970-），女，教授，从事复杂网络的应用性研究。E-mail：fy_lnlzy@163.com。